劈裂环-盘二聚体结构的多重Fano共振*
杨其利 张兴坊2)† 刘凤收 闫昕2) 梁兰菊2)
1) (枣庄学院光电工程学院,枣庄 277160)
2) (山东省光电信息处理与显示实验室,枣庄 277160)
利用时域有限差分方法,理论研究了由劈裂环和圆盘构成的金二聚体结构的光学性质,分析了劈裂环的缺口取向和对称性破缺程度对其Fano共振特性的影响.结果表明,当缺口方向平行于二聚体中心连线时,劈裂环的奇数阶和偶数阶模式均能与圆盘的偶极模式作用产生Fano共振,且随着劈裂环的进一步破缺,更多的偶数阶Fano共振能被激发出来;但当垂直时,不管劈裂环的缺口背对圆盘还是面向圆盘,二聚体仅有偶数阶Fano共振能被激发出来,且随着劈裂环内层中心远离圆盘而增强,随着劈裂环的进一步破缺,缺口背对圆盘的二聚体还能激发出多个奇数阶Fano共振,但同时也引起偶数阶Fano共振的减弱,而缺口面向圆盘的二聚体则仅发生偶数阶Fano共振的略微增大.这些结果可望对基于多重Fano共振的多波段光子器件设计有一定的参考意义.
1 引言
众所周知,金属表面等离激元共振效应可以突破光学衍射极限,将传统光学微观结构从光的波长量级压缩到亚波长尺度,为实现光子器件的微型化提供理论依据[1].在合适条件下,纳米结构中具有较大辐射展宽的亮模式和具有窄带特性的暗模式还可通过近场耦合等作用,相消干涉产生Fano共振效应等,这奇特的光学性质为新型光子器件的探索和设计提供了更多的研究思路.例如,在Fano共振波长处辐射阻尼由于受到显著抑制而导致的陡峭的不对称光学响应谱线,其对环境折射率的变化极为敏感,这使得它在生物化学传感器[2]、光学开关[3]和纳米天线[4]等方向有着广阔的应用前景.同时,Fano共振由于弱辐射阻尼特性使得入射场能量束缚在纳米结构周围,产生的极强局域场增强可以在纳米尺度提高电磁波与物质的相互作用效率,从而有利于许多非线性现象的实现,如表面增强光谱[5]和谐波产生[6]等.目前,已在单体[7]、二聚体[8]和三聚体[9]到低聚物[10]甚至更大的团簇[11]等多种类型的微纳结构中观察到了Fano共振现象,并发现其光学行为高度依赖于结构的化学组分、几何参数、空间分布及介电环境等.
为突破单频Fano共振在光学器件应用上的限制,纳米结构多重Fano共振的激发,由于能同时在多个波段控制光与物质的相互作用,在多波段滤波器、高灵敏生化传感器等方面有着重要的应用[12],吸引了越来越多的关注.当前获得多重Fano共振的方法可分为两类,第一类为利用多个颗粒组成的低聚物或团簇体系,这主要归因于体系内存在不同颗粒之间异相电荷振荡导致的多个暗模式与多数颗粒同相振荡形成的亮模式的相互作用[10];第二类为运用体系的亮模式激发大尺寸颗粒自身内在的暗多极模式,典型构筑单元为环结构.该结构不仅能将入射光局域在环的内外壁,而且还能通过内外径、壁厚等多个参数调控其近场和远场响应[13,14].相比于完整环结构,劈裂环由于缺口的存在对光场的调制提供了更多的自由度,其不仅能与入射光直接作用激发出高阶电磁共振使得光谱更加精细[15,16],而且在劈裂缺口处还能够形成较大的电场增强从而导致非线性光学效率的提升[17].当改变入射光的偏振时,还可进一步改变劈裂环缺口处的电场强度和调整其空间分布[14].当一个尺寸相对较小的颗粒插入到较大的劈裂环中时,添加的颗粒与环的各种固有模式之间将相互作用产生多个低能成键和高能反键共振态[18,19],很可能导致共振频率靠近的亮模式和暗模式满足Fano共振条件.文献[20]报道了在三角板与劈裂环构成的纳米结构中,三角板的偶极模式与劈裂环的四极模式杂化形成的成键暗模式和反键亮模式,可相互作用形成Fano共振.文献[21]表明劈裂环偶极与圆盘偶极同相振荡而产生的高能反键亮模式,其可同时与劈裂环的四极和八极模式耦合,实现双重Fano共振的激发.此外,通过调节插入的纳米颗粒和劈裂环之间的耦合程度,还可以控制不同类型Fano共振的产生.如在劈裂环/棒结构中,利用纳米棒的移动,可以调控基于劈裂环对称或反对称四极模式的Fano共振的形成[22];在劈裂环/盘纳米腔中,纳米圆盘在不同方向上的位移可诱导出第二个对称或反对称Fano共振[23].另有报道[24,25],通过破坏环宽度的均匀性,可以在不对称劈裂环/盘纳米结构中产生更丰富的Fano共振现象,原因在于腔的电偶极亮模对劈裂环更多个暗高阶模的激发.
尽管基于劈裂环的多重Fano共振等离激元微纳结构已有许多报道,但多集中于研究外来颗粒嵌入到劈裂环中时的腔结构参数对Fano共振的影响,对于颗粒在劈裂环之外构成的二聚体结构的Fano共振多重激发、调控等工作尚较少见.本文通过时域有限差分(finite difference time domain,FDTD)方法,研究由圆盘与劈裂环构筑的金二聚体结构的光学性质,分析劈裂环的缺口取向、破缺程度等对其多重Fano共振调谐特性的影响.结果发现,该二聚体具有较强的Fano共振可调控性,通过不同程度的二聚体结构对称性破缺,将导致不同类型的多重Fano共振的激发和强度改变,这为多波段滤波和传感应用提供了一定参考.
2 模型与计算方法
图1为所研究的劈裂环-盘二聚体的几何结构示意图.圆盘的半径R=150 nm,劈裂环的内外层半径分别为R1=170 nm和R2=200 nm,缺口角度θ=30°,两者的间隔g=10 nm,高度均为30 nm.参量φ为劈裂环缺口中心相对y轴的偏转角度.根据文献[21,26]的描述,劈裂环的缺口方向定义为缺口两端对应位置的连线方向,当φ=0°时其平行于二聚体中心连线,即沿x轴方向;当φ=90°或–90°时,缺口方向垂直于中心连线,即沿y轴方向.参量Δx和Δy表示劈裂环的内层中心相对外层中心分别沿x轴和y轴方向的偏移量.二聚体的光学性质采用FDTD方法[27]模拟得到,为了模拟准确将该二聚体的计算区域设定为3500 nm × 3500 nm × 3000 nm,网格尺寸设置为2.5 nm,并在边界上构建完全匹配层以阻隔反射光.劈裂环和圆盘的材料均为金,其折射率数据取自于文献[28],周围环境设置为空气.入射电磁波沿z轴垂直照射于该二聚体,偏振方向平行于x轴.另外,除非特别指出,本文中所涉及的二聚体表面电场分布描绘的均是在z轴方向的电场分量(Ez)图像,这是因为纳米结构表面电场的法向分量方向与电荷的分布相关[29],从而可以间接确定纳米结构共振模式的类别.且为了更清晰地展示电场分布特点,每个电场图上的色阶不同.
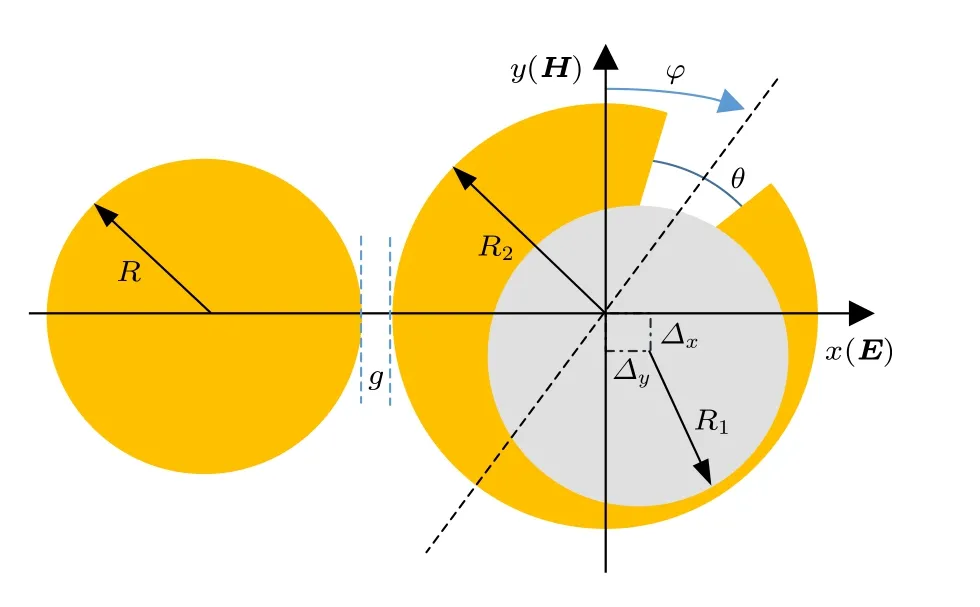
图1 劈裂环-盘二聚体的几何结构示意图,其中R=150 nm,R1=170 nm,R2=200 nm,θ=30°,g=10 nm,二聚体高度为30 nmFig.1.Geometrical structure of the split ring-disk dimer,where R=150 nm,R1=170 nm,R2=200 nm,θ=30°,g=10 nm,the height of dimer is 30 nm.
3 结果与讨论
纳米结构的光学性质与其几何结构参数密切相关.在其他参数固定不变的情况下,参量φ,Δx和Δy的变化均可能引起二聚体光学性质的变化.下面将分别计算当缺口方向与x轴平行(φ=0°)或垂直(φ=90°,–90°)时,劈裂环内层中心的移动引起的二聚体散射谱的变化,分析该结构的Fano共振调控性质.
首先,分析φ=0°和Δx=Δy=0 nm时该二聚体结构的光学性质,其和具有相同物理参数的单独圆盘、单独劈裂环的散射谱如图2所示.由图2可知,单独圆盘在857 nm附近产生的散射峰由其偶极共振所导致,单独劈裂环在1265 nm,849 nm和693 nm附近的散射峰,分别对应劈裂环的3个共振模式.可见,与正入射时完整环仅能激发偶极模式相比[13],劈裂环因为结构对称性的破缺,其高阶模式能够与入射光直接耦合从而产生多个高阶电磁共振,而且由于劈裂环的后两个高阶模式处于圆盘的偶极共振光谱范围内,满足Fano共振条件,故导致二聚体在857 nm和724 nm处产生了两个Fano共振谷(标记为aDip5和aDip7).为进一步探究该Fano共振产生的物理原理,图2右侧中、下插图分别展示了在两个Fano共振谷位时激发的该二聚体表面电场分布.可以看到,劈裂环表面分别存在5个和7个电场节点且缺口两端电场方向相反,表现为五阶(N=5)和七阶(N=7)共振模式[24],也被称为反对称八极和十六级模式[22,23],这两个奇数阶模式与圆盘偶极模式发生相消干涉从而引起了五阶(反对称八极)-偶极和七阶(反对称十六极)-偶极Fano共振的产生.对于单独劈裂环在1265 nm处产生的共振,其与圆盘的偶极共振光谱重叠度较小,故未引起明显的Fano共振效应.根据图2右上插图展示的在1373 nm时激发的该二聚体表面电场分布可以看出,该模式对应于劈裂环的三阶共振(N=3,反对称四极)模式[22,25].其与圆盘的偶极模式作用将形成高能量的三阶-偶极反键模式和低能量的成键模式,后者具有更大的净偶极矩,与入射光耦合形成了在1373 nm附近的强散射峰(aPeak3).此外,从图2还看到二聚体在993 nm附近显现了一个较深的共振谷(aDip4),该处激发的电场分布如图2左侧插图所示.可见,此时劈裂环表面存在4个电场节点且缺口两端的电场方向相同,表明该共振对应于劈裂环的四阶(N=4,对称四极)模式.一般,当入射光偏振方向平行于单独劈裂环的缺口方向时,只有劈裂环的奇数阶模式能够被激发出来,产生一阶(N=1)、三阶、五阶等共振[26],而偶数阶模式作为一种完全暗模式,通常不能被激发出来.但是,当劈裂环与圆盘组成二聚体结构时,劈裂环的四阶暗模式可通过近场耦合作用被圆盘的偶极亮模式激发出来,并与之发生相消干涉产生四阶-偶极Fano共振谷.相比于完整环盘二聚体只能激发一个四极Fano共振[30],劈裂环盘二聚体因为缺口的存在可激发出对称和反对称两种类型的四极Fano共振,使得光谱更加精细,更有利于在多波长传感器件中激发波段的选择.

图2 当φ=0°和Δx=Δy=0 nm时二聚体、单独圆盘和单独劈裂环的散射谱.插图为对应共振波长处激发的二聚体表面电场Ez分布Fig.2.Scattering spectra of a single dimer,individual disk and individual split ring with φ=0° and Δx=Δy=0 nm.Insets show the calculated electric field distributions Ez on the surface of the dimer at the indicated resonances.
当劈裂环的内层中心与外层中心不一致,即Δx≠ 0或Δy≠ 0时,环宽度的不均匀性将导致二聚体结构的对称性进一步破坏,进而引起其Fano共振特性发生变化.图3给出了φ=0°和Δy=0 nm时,Δx的变化引起的二聚体散射谱的演变.由图3(a)可见,随着Δx的增大,整个光谱红移,处于四阶-偶极Fano共振谷(aDip4)和三阶-偶极成键共振峰(aPeak3)之间的弱峰(aPeak3')和浅谷(aDip3)逐渐增大,对应波长分别从Δx=0 nm时的1100 nm和1142 nm移动至Δx=20 nm时的1164 nm和1279 nm.同时,在短波长区域的七阶-偶极Fano谷(aDip7)逐渐变小并在Δx=15 nm时消失,而在其临近的长波长处的散射峰则发生了分裂,产生了一个新谷(aDip6).此外,在1862 nm附近还出现了一个新的共振峰(aPeak2).为了解释该现象产生的原因,计算了单独劈裂环在Δx=20 nm时的散射谱,如图3(a)中黑细线所示.该谱线上共显示了4个明显的散射峰和1个处于短波长区域的较弱的峰,对应波长分别为1824,1361,1054,903和736 nm.根据等离激元杂化理论[16],当劈裂环的结构对称性破缺时,不同能级的内外层表面等离激元共振将发生耦合,使得劈裂环的高阶模式能够与偶极模式杂化而被激发,同时引起散射峰红移.因此,随着Δx从0 nm增大至20 nm,劈裂环的三阶、五阶和七阶模式共振波长分别红移至1361,903和736 nm;其偶数阶暗模式也被激发并随着增强,当Δx=20 nm时1824 nm和1054 nm附近的散射峰分别源于劈裂环的二阶(N=2,对称偶极)和四阶共振模式.在二聚体结构中,劈裂环的二阶模式进一步与圆盘的偶极模式杂化而形成了在1862 nm附近的散射峰(aPeak2),其对应的电场分布如图3(a)右上插图所示.可以看出,沿劈裂环表面存在三个电场节点,与三阶模式的电场分布类似,但缺口右端的电场强度和分布区域明显小于左端的电场,这是由于此时产生的劈裂环二阶模式也杂化了一阶和三阶等奇数阶模式,从而导致缺口两端的电场强度和方向不同.至于在1164 nm附近的共振(aPeak3'),由其电场分布(右中插图)可知,该共振对应于劈裂环三阶模式和圆盘偶极模式杂化而形成的反键模式.随着Δx的增大,反键模式强度逐渐增大,成键模式强度逐渐减小,两者之间的相互作用形成一个逐渐增大的三阶-偶极Fano共振谷(aDip3),结果类似于环二聚体产生的四极-偶极Fano共振谷随环厚度的演变[31].而二聚体在Δx=20 nm时816 nm附近出现的新谷(aDip6),没有对应的单独劈裂环散射峰出现,但其处于劈裂环的五阶和七阶散射峰之间,推测该新谷源于劈裂环所支持的六阶(N=6)暗模式与圆盘偶极模式作用而导致的六阶-偶极Fano共振.图3(a)右下插图显示了在该谷位处激发的二聚体表面电场分布,可见沿劈裂环表面共有6个电场节点且缺口两端的电场方向相同,证实了劈裂环六阶模式的产生.有意思的是,尽管七阶-偶极Fano共振谷随着Δx的增大逐渐减小并消失,但在Δx=25 nm时将又重新出现且八阶(N=8,对称十六级)-偶极Fano共振也能被激发出来 (图3(a)中未给出).

图3 固定φ=0°和Δy=0 nm,二聚体的散射谱随(a) Δx=0—20 nm,(b) Δx=–20—0 nm的变化.插图为在指定频率处的二聚体表面电场分布Fig.3.Scattering spectra of the dimer with φ=0° and Δy=0 nm for different values of Δx:(a) Δx=0–20 nm;(b) Δx=–20–0 nm.Insets show the calculated electric field(a) Ez(Δx=20 nm),and (b) |E| (Δx=–20 nm) distributions at the indicated resonances.
当劈裂环内层相对外层沿x轴负方向移动时,二聚体的散射谱随Δx的变化如图3(b)所示.可以看到,随着Δx的减小,散射谱也红移,但各个Fano共振谷却随着减小,七阶-偶极Fano共振谷(aDip7)在Δx=–20 nm时已变得很浅,而五阶-偶极和四阶-偶极Fano共振谷(aDip5、aDip4)在Δx=–15 nm时已消失不见;同时,六阶-偶极Fano共振谷(aDip6)在Δx=–10 nm时出现但变化很小.通过对比Δx=–20 nm和0 nm时在七阶-偶极Fano共振谷(aDip7)处激发的电场强度|E|分布可发现,相比于Δx=0 nm时,Δx=–20 nm时的圆盘左端产生的局域电场相对较强,同时劈裂环缺口两端的电场相对较弱,说明当Δx减小时圆盘的偶极模式能量不能相对有效的耦合到劈裂环中,导致Fano共振效应减弱.这里,为了方便对比,两个插图中的电场强度|E|分布采用了相同的色阶设置.结合图3(a)和3(b)可知,当劈裂环内层相对外层平行于缺口方向移动时,远离圆盘方向能获得相对精细的散射谱型,并可根据需要对Fano共振进行选择和调制.
图4给出了当φ=0°和Δx=0 nm时,Δy的变化对该二聚体结构散射谱的影响.由图4可见,不管Δy由0 nm增大还是减小,整个光谱均向长波长方向移动,且Δy=–20 nm时的红移程度比Δy=20 nm时稍大,并均伴随着六阶-偶极Fano共振谷(aDip6)的出现.但是,Δy由0 nm增大和减小对原有Fano共振谷的影响有着明显的不同,随着Δy由0 nm增大,除七阶-偶极Fano共振谷(aDip7)外,其他Fano共振谷均逐渐减小并在Δy=20 nm时不可分辨;而随着Δy由0 nm减小到–20 nm,七阶-偶极Fano共振谷(aDip7)减小并消失,五阶-偶极Fano共振谷(aDip5)在Δy=–10 nm时强度几乎没变,但在Δy=–20 nm时明显变小,而四阶-偶极和三阶-偶极Fano共振谷(aDip4、aDip3)则随着增大.这说明当劈裂环的内层中心垂直于缺口方向移动时,不管靠近还是远离缺口均有利于基于劈裂环偶数阶模式的Fano共振的激发,但靠近和远离缺口对原有Fano共振的影响则不同,当靠近缺口时圆盘的偶极模式与劈裂环的低阶模式间的耦合强度减小,圆盘能量不易于耦合进劈裂环中,从而导致Fano共振效应减弱;当远离缺口时圆盘偶极模式却能相对有效的与劈裂环低阶模式发生耦合,使得对应的Fano共振谷增大,但此时与劈裂环高阶模式间的耦合效果则相对较差.此外,由图可知,Δy=–10 nm时的散射谱上存在较多的Fano共振谷,可能更有利于多波段生化传感应用[32].

图4 固定φ=0°和Δx=0 nm,Δy在–20—20 nm变化时二聚体散射谱的变化Fig.4.Scattering spectra of the dimer with φ=0° and Δx=0 nm for different values of Δy=–20–20 nm.
当φ=90°时,图5(a)给出了固定Δx=0 nm,该二聚体结构的散射谱随Δy的变化.由图可 见,当Δy=0 nm时,在散射谱775 nm和989 nm处分别出现了较明显的Fano共振谷(分别标记为bDip6,bDip4),在1901 nm处则显示了一个具有较宽谱宽的共振峰(bPeak2).为了分析其产生机制,图5(b)第一行分别给出了相应波长处激发的二聚体表面电场分布.可见,此时图中每个劈裂环缺口两端产生的电场方向均相同,且沿劈裂环表面分别存在6个、4个和2个电场节点.表明当φ=90°时劈裂环中的偶数阶模式可被激发出来,且六阶和四阶模式还能够与圆盘的偶极模式相消干涉产生六阶-偶极和四阶-偶极Fano共振谷(bDip6、bDip4),而二阶模式则和圆盘偶极模式耦合形成成键二阶-偶极模式,使得净偶极矩增大,增强了对入射光的散射能力.相比φ=0°时可同时产生奇数阶-偶极和偶数阶-偶极Fano共振,此时的二聚体散射谱中未能发现奇数阶-偶极Fano共振的存在,可能原因在于φ=90°时的二聚体结构关于x轴对称,对称性相对较好,因而劈裂环和圆盘模式之间的等离激元共振杂化条件相对严格,导致劈裂环奇数阶模式与圆盘偶极模式之间的耦合强度相对较弱,不足以满足此类型的Fano共振产生条件.由图5(a)还可见,随着Δy的增大,光谱红移,六阶-偶极Fano共振谷(bDip6)先减小后消失但在Δy=20 nm时又重新出现,四阶-偶极Fano共振谷(bDip4)则随着单调减小且在Δy=20 nm时已不可分辨;同时,在散射谱的短波长波段出现了几个新谷(bDip5,bDip7,bDip8),当Δy=20 nm时对应波长分别为916nm,756 nm和705 nm.根据图5(b)第二行所展示的在新谷处激发的电场分布可看出,这几个新谷分别源于劈裂环的五阶、七阶和八阶模式与圆盘的偶极模式耦合而产生的Fano共振.另外,由图5(b)第三行插图还可知,劈裂环的三阶模式也随着Δy的增大而被激发出来,由于其远离圆盘的偶极模式,故显示为一个共振峰(bPeak3)的形式.这些现象可解释为,当劈裂环内层中心平行缺口方向移动时,二聚体结构关于x轴的对称性被破坏,劈裂环和圆盘模式之间的等离激元共振杂化条件放宽,使得劈裂环奇数阶暗模式能够与圆盘偶极模式发生耦合,导致了奇数阶-偶极Fano共振的产生,且可能由于模式竞争的关系[33],同时引起了偶数阶-偶极Fano共振的减弱.

图5 固定φ=90°,二聚体的散射谱随(a) Δx=0 nm,Δy在0—20 nm,(c) Δy=0 nm,Δx在–20—20 nm改变时的变化;(b)在图(a)散射谱Δy=0 nm或20 nm中指定频率处的二聚体表面电场分布Fig.5.Scattering spectra of the dimer with φ=90° for different values of (a) Δyfrom 0 nm to 20 nm with Δx=0 nm,and (c) Δx from–20 nm to 20 nm with Δy=0 nm;(b) calculated electric field Ez distributions at the indicated resonances shown in Fig.(a) at Δy=0 nm and 20 nm.
图5(c)给出了当φ=90°并保持Δy=0 nm固定不变时,该二聚体结构的散射谱随Δx的变化.由图可见,随着Δx由0 nm减小,四阶-偶极和六阶-偶极Fano共振谷均减小,当Δx=–20 nm时四阶-偶极Fano共振谷(bDip4)已不可分辨,六阶-偶极Fano共振谷(bDip6)也只显示为一个很小的谷;而当Δx由0 nm增大时,这两个Fano共振谷略有增大,且当Δx=20 nm时在696 nm附近还出现了一个新谷(bDip8).根据该谷位处激发的二聚体表面电场分布可知,此新谷源于劈裂环的八阶模式与圆盘偶极模式耦合而产生的八阶-偶极Fano共振.这说明当劈裂环内层中心垂直缺口方向移动时,由于二聚体结构仍然关于x轴对称,故仅能产生偶数阶-偶极Fano共振,且越靠近缺口(远离圆盘)越有利于Fano共振的增强.
图6(a)给出了当φ=–90°和Δx=0 nm时,该二聚体结构的散射谱随Δy的变化.由图可见,当Δy=0 nm时,两个明显的Fano共振谷分别出现在756 nm(cDip6)和972 nm(cDip4)附近,另有一个具有较宽谱宽的共振峰出现在1789 nm附近(cPeak2).根据图6(a)插图中显示的在对应波长处激发的二聚体表面电场分布可看出,这两个Fano共振谷分别源于劈裂环的六阶和四阶模式与圆盘偶极模式相消干涉而产生的Fano共振,共振峰则源于劈裂环的二阶模式和圆盘偶极模式形成的成键二阶-偶极模式.相比于φ=90°时的散射谱,此时的二聚体散射谱相对蓝移,原因在于φ=–90°时的劈裂环缺口取向使得圆盘与劈裂环之间的间隙相对较大,导致圆盘偶极模式与劈裂环模式间的耦合相对较弱.随着Δy的增大,光谱红移,六阶-偶极和四阶-偶极Fano共振谷略有增大,三阶-偶极模式也随着出现并增大.这与φ=90°时的光谱随Δy的变化有所不同,可能原因在于圆盘偶极模式和劈裂环奇数阶模式之间的耦合强度还是相对较弱,不足以满足奇数阶-偶极Fano共振激发条件.图6(b)为当φ=–90°和Δy=0 nm时,Δx的变化对二聚体散射谱的影响.可见,当Δx增大时,六阶-偶极和四阶-偶极Fano共振谷将增大,同时八阶-偶极Fano共振也能被激发出来.这与φ=90°时Δx的变化对二聚体散射谱的影响类似,但当Δx同等程度变化时,φ=90°时的Fano共振谷强度变化要比φ=–90°时的变化大些,根源就在于组成二聚体结构的劈裂环与圆盘之间的间隙不同,间隙越小,则劈裂环和圆盘间的耦合效应越大,对参数的变化也越敏感,导致的光学性质变化程度也越大[34].

图6 当φ=–90°时二聚体的散射谱随Δx,Δy的变化(a) Δx=0 nm,Δy从0 nm到20 nm;(b) Δy=0 nm,Δx从–20 nm到20 nm.插图为Δx=0 nm,Δy=20 nm时的散射谱中指定频率处的二聚体表面电场分布Fig.6.Scattering spectra of the dimer with φ=90° for different values of (a) Δy from 0 nm to 20 nm with Δx=0 nm,and (b) Δx from–20 nm to 20 nm with Δy=0 nm.Inset show the calculated electric field Ez distributions at the indicated resonances with Δx=0 nm and Δy=20 nm.
值得指出的是,虽然通过调节结构参数可实现对劈裂环盘二聚体多重Fano共振的激发,但产生的Fano共振存在着调制深度较浅、光谱对比度相对较差的缺点,制约着相关器件的实际应用.有文献报道当纳米结构组成阵列时,阵列单元之间的耦合效应可对Fano共振线型进行调控[9,35].因此,探究了劈裂环盘二聚体阵列结构的光学性质,发现二聚体组成阵列时能够使得Fano共振光谱对比度增大,且阵列周期越小Fano共振对比度也越好,表明相比单个盘环二聚体,其阵列结构能够有效提升对入射光场的调制能力.阵列结构参数对于该二聚体阵列多重Fano共振的具体影响,我们将在以后继续讨论.
4 结论
本文研究了一种由金劈裂环和金圆盘构成的环盘二聚体结构,应用FDTD方法模拟了其散射光谱和表面电场分布,分析了劈裂环的缺口取向、对称破缺程度等对其光学性质尤其是Fano共振特性的影响.结果表明,该结构能够激发多重Fano共振,且随着劈裂环破缺程度增大而红移.当劈裂环的缺口方向平行于二聚体中心连线时,基于劈裂环奇数阶和偶数阶的Fano共振均能被激发出来,且劈裂环的进一步破缺还有利于偶数阶Fano共振的产生.此外,随着劈裂环内层中心远离圆盘散射谱形将变得更加精细,低阶Fano共振也随着内层中心远离缺口而增大.当劈裂环的缺口方向垂直于二聚体中心连线时,仅能激发出基于劈裂环偶数阶的Fano共振,且随着劈裂环内层中心远离圆盘而增大,当劈裂环进一步破缺时,缺口背对圆盘的二聚体结构还能激发出奇数阶Fano共振,同时伴随着偶数阶Fano共振的减弱,而缺口面对圆盘的二聚体则仅发生偶数阶Fano共振的微增.这些结果可望用于基于多重Fano共振可控的劈裂环盘二聚体结构设计,以满足多波段微纳光子学方面的需求.

