外加应力作用下 UO2 中空洞演化过程的相场模拟*

姜彦博 柳文波† 孙志鹏 喇永孝 恽迪

1) (西安交通大学核科学与技术学院,西安 710049)

2) (中国核动力研究设计院,核反应堆系统设计技术重点实验室,成都 610213)

本工作建立了外加应力作用下UO2中空洞演化的相场模型.首先,使用摄动迭代法求解了弹性平衡方程,对外加应力下单个空洞周围的应力分布进行了计算,结果表明空洞边缘有应力集中现象,模拟得到的应力分布和解析解一致.然后,利用相场方法模拟了不同外加应力下单个空洞的演化过程,结果表明随着外加应力的增大,空洞的生长速度加快.最后,研究了外加应力对多晶体系中晶粒长大和空洞演化的影响,结果表明,不同晶粒内的应力大小不同,应力越小的晶粒越容易长大,尺寸越大的空洞的边缘应力也越大.晶间空洞与弯曲晶界存在相互作用,一方面晶界附近的空洞会生长成透镜状,另一方面空洞对晶界也有钉扎作用,能减缓晶界的迁移.此外,外加应力会加速多晶系统中空洞的生长,并且本文计算得到了外加应力与空洞半径的关系,发现外加应力越大,空洞的生长越快.

1 引言

二氧化铀(UO2)燃料是一种非常重要的核燃料,有熔点高、热循环稳定性好、中子经济性好、与包层和冷却剂相容性好等很多优点[1].燃料在长时间的服役环境下,级联碰撞会产生大量的空位和间隙原子等点缺陷,点缺陷的迁移、聚集、长大会形成空洞等缺陷组织,从而进一步导致核燃料辐照肿胀,并严重影响其服役性能[2].陶瓷型UO2燃料一般通过烧结方法制备,烧结时晶粒长大、烧结颈的闭合等过程也不可避免地会在燃料中引入大量空洞等缺陷[3],这些空洞也会对陶瓷燃料的服役性能造成严重影响.因此,研究核燃料中空洞的演化对揭示燃料服役过程中的组织演变行为具有重要意义.

核燃料通常在高温和强辐照的极端环境中服役,此时燃料产生的蠕变应变和热应变使其承受的应力显著增大[4],因此研究燃料在应力作用下的微观组织演化十分重要[5−10].Brask[5]通过注氦不锈钢的退火实验研究了不同拉应力对氦泡生长速率的影响,研究表明,外加拉应力促进了晶界滑移,而且晶界处的氦泡有更大的尺寸,但外加应力对晶内氦泡的影响较小.此后,对不锈钢中空洞演化的一系列实验研究[6−8]也表明,外加应力会加速空洞的形核和生长,但是应力增强空洞生长和辐照肿胀的微观机制尚不明确.近年来,大量研究表明晶界对空洞的演变也有重要影响.一方面,晶界作为缺陷的强吸收阱(sink),对其附近的空位和间隙原子有很强的吸收作用,从而影响晶界附近的空洞形貌.例如,在晶界附近观察到了无空洞区和与之相邻的空洞峰值区[9].另一方面,晶界作为点缺陷扩散迁移的高速传输通道,其中大量空位被晶间空洞捕获,导致晶间空洞尺寸一般远大于晶内空洞[10].因此,研究外加应力下多晶中的空洞演变行为尤为重要.

空洞的演化包含形核、生长和粗化等过程,经典形核理论可以确定空洞的形核速率和密度,而速率理论可用于确定空洞和间隙团簇的生长速率[11,12].速率理论是基于“反应”的动力学规律建立的速率方程,其建模和计算过程需要提供很多相互作用系数作为输入条件.然而,该模型以空间平均场的方式处理空洞的动力学演化,在提高计算效率的同时忽略了各种微观结构特征以及应力、温度等外部因素的空间关联性.相比于速率理论来说,相场方法不仅同时考虑了热力学和动力学两方面因素,而且具有时间与空间的特征,可以追踪到动态的演变过程.因此,需要在介观尺度上开发材料辐照微观结构演化的包含空间特征的相场模型,以更好地理解微观结构和空洞演化过程.

近年来,作为介观尺度的有力工具,相场方法在材料微观组织演化研究中广泛应用[13−20].相场方法既可以包含界面、晶粒和缺陷等微观信息,又可以动态捕捉模拟过程中微观组织的形貌演变,在解决非均匀微观结构产生的弹性相互作用方面有独特的优越性.Hu和Chen[17]提出了一个有效的扩散界面相场模型,使用数值迭代方法求解了弹性平衡方程,达到了很好的精度.Wang等[18]提出了一种求解弹性能各向异性和非均匀体系中弹性平衡方程的方法.该方法通过假设等效本征应变在模拟体系中是均匀分布的,来确定位移场和等效本征应变场,然后使用获得的位移场作为迭代方法的零级近似.Kim等[19]将弹性不均匀性纳入晶粒长大的相场模型,并研究了外部载荷作用下的晶粒长大和织构演变过程.Chang等[20]在空洞演化相场模型的基础上引入了非均匀弹性能来研究外加应力的影响,发现随着外加应力的增加,空洞肿胀加快.目前,UO2燃料中与应力有关的研究主要集中在裂纹和断裂的力学性能分析等方面.Salvo等[21]详细介绍了在高温下进行的一系列应变率控制压缩试验的结果,表明样品中心的孔隙率随应变率增大而增大.然而,外加应力对多晶UO2燃料中空洞演化行为的研究有待进一步推进.

本文建立了外加应力下UO2中空洞形貌演化的相场模型.首先,通过摄动迭代算法求解应力平衡方程,对单个空洞周围的应力分布进行了计算;然后,利用相场方法模拟了不同应力下的空洞生长过程,进一步计算了不同外加应力下的应力分布和弹性能分布;最后,把模型应用于含有晶间空洞的双晶体系和多晶体系,研究外加应力对多晶UO2中晶界移动和空洞演化的影响.

2 相场模型

2.1 相场自由能方程

本工作基于相场理论,建立外加应力作用下空洞演化及其与晶界相互作用的理论模型.模型中引入保守场变量cv来描述空位浓度.该变量被用于区分系统中包含的两个相,分别是cv1.0 的空洞相和cv的基体相,其中为空位平衡浓度.同时,使用非保守场变量ηi(i1,2,···,p) 来描述p个不同取向的晶粒,在第i个有特定取向的晶粒中ηi取值为1,其余位置均为0.所有的相场变量在晶界和空洞表面等界面处是连续变化的,即各相场变量在晶界和相界上具有一个扩散型界面.

相场理论用各组成相和界面的自由能来表示非均匀材料的总自由能泛函,该泛函用于推导相场变量的动力学方程.本文使用的相场模型中,非均匀体系的总自由能泛函F表示与相场变量相关的体自由能、多晶自由能、弹性应变能和梯度自由能之和.根据Cahn-Hilliard对非平衡多相体系自由能的定义[22],系统的总自由能密度F为[2]

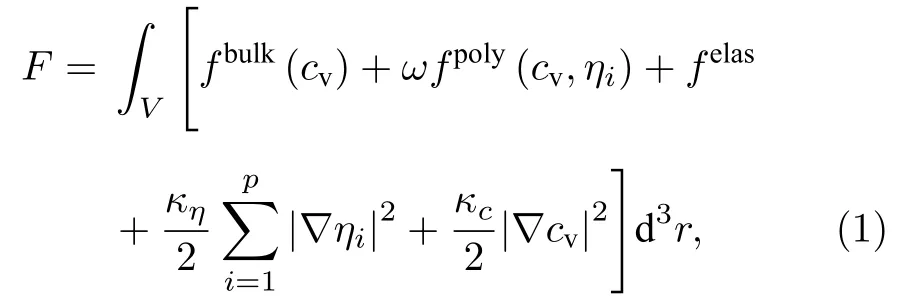
式中,fbulk为体自由能密度函数,fpoly为多晶相互作用能密度函数,ω为势垒高度,felas为弹性应变能密度函数;等式右边后两项为梯度自由能密度,κη和κc分别为非保守场和保守场的梯度项参数,cv为空位浓度(保守场),ηi为晶粒取向序参量(非保守场).体自由能密度函数fbulk的表达式如下[10]:

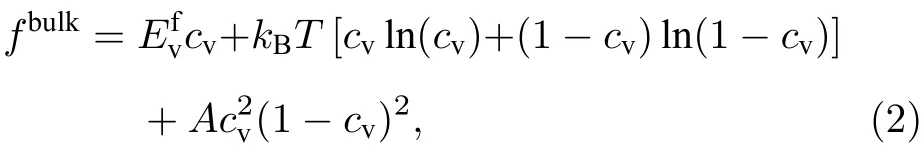
式中,为空位形成能,kB为玻尔兹曼常数,T为绝对温度,A为双势阱函数的势垒高度,本文取值为1.0.多晶自由能fpoly的表达式如下[23]:

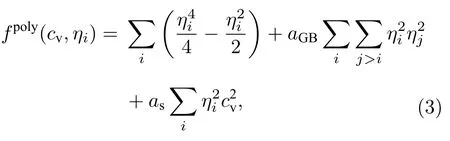
式中,aGB和as分别为与基体晶界能和空洞表面能相关的的参数,它们的关系为asaGBγs/γGB,其中γs为空洞表面能,γGB为基体晶界能.

弹性应变能felas由与位置相关的弹性模量和系统各应变表示[24]:

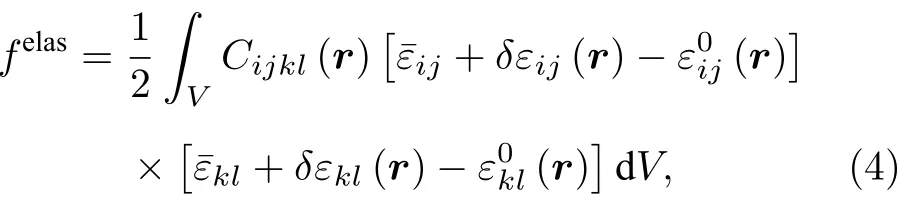
式中,Cijkl(r)为与位置相关的弹性模量,为均匀应变,δεij(r)为非均匀应变,(r) 为本征应变.在多晶材料中,弹性模量可以与晶粒的相对取向建立关系:每个晶粒的弹性模量可以由相对于固定坐标系的变换张量获得[25].设为固定参考体系中的单个晶粒的弹性模量,为空洞中弹性模量.本文假设空洞相的弹性模量很小,取10−4.系统中与位置相关的弹性模量表达式如下[26]:

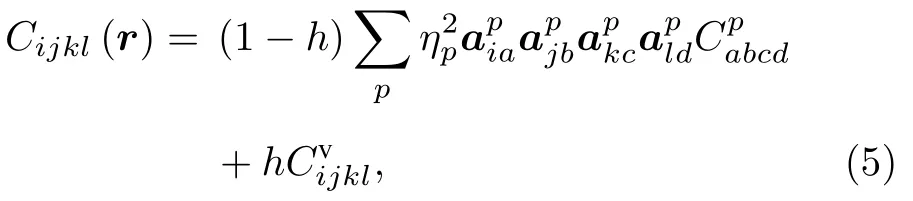
式中,h为与空位浓度相关的插值函数,h−(m,n1,2,3) 表示给定晶粒p相对于参考坐标系的旋转矩阵.三维空间中,该矩阵由给定晶粒的欧拉角θ,ψ和ξ确定[27]:

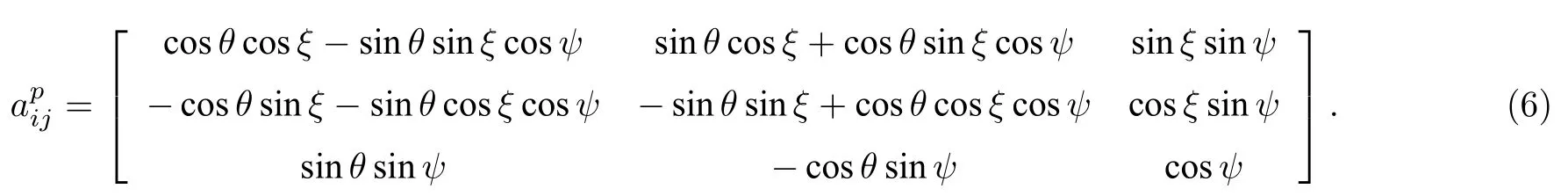
本文的工作在二维空间中进行,所以角度ψ和ξ均为零.此外,与位置相关的弹性模量Cijkl(r)可以写成均匀弹性模量和非均匀弹性模量之和:

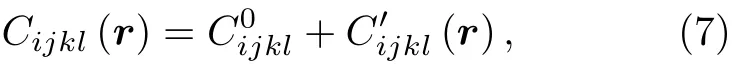
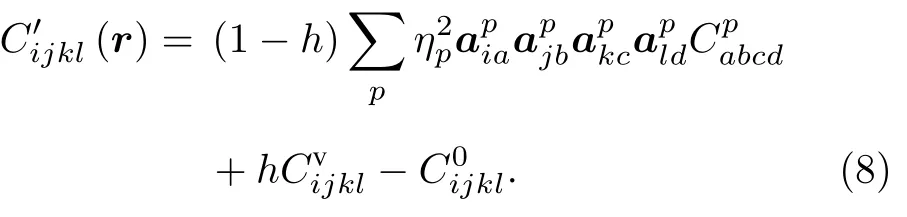
引入εij(r) 表示相对于未变形晶格的总应变,根据线性弹性假设,局部应力σij(r) 可以表示为(r)

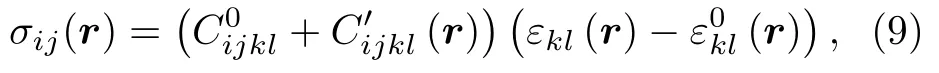
式中,是本征应变场,用于表示非弹性应变部分.本模型不考虑非弹性应变,因此本征应变设置为零.本工作中使用的应力为正时,表示垂直于空洞表面向外的拉应力;而使用的应力为负时,表示垂直于空洞表面向内的压应力.通过求解力学平衡方程可以得到应力和应变的分布:

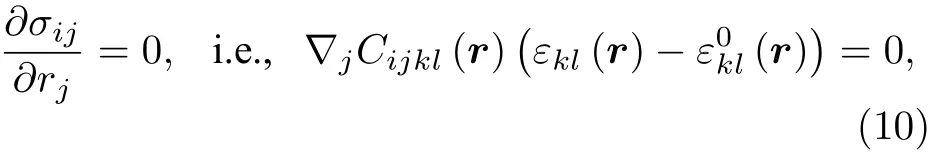
式中,总应变εkl(r) 可以表示为均匀应变和非均匀应变的总和:

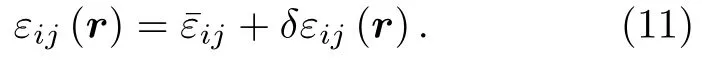
均匀应变表达式如下[28]:

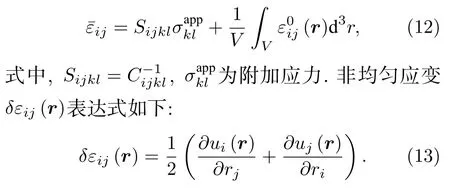
把(13)式代入 (10) 式中得到

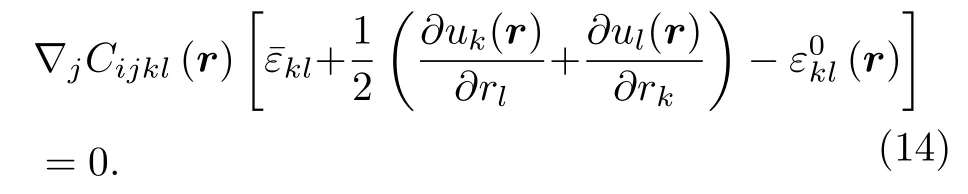
简化整理后得到位移场方程:

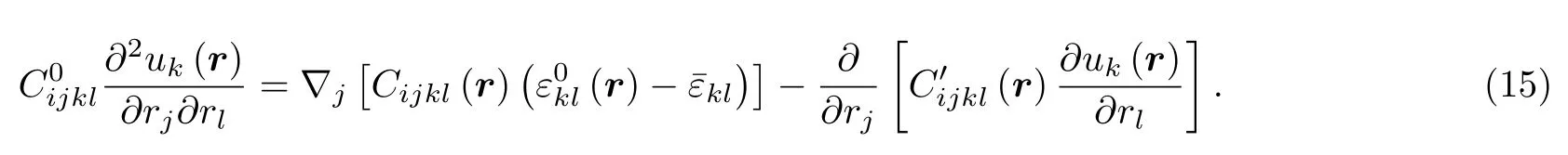
对(15)式进行傅里叶变换后得到

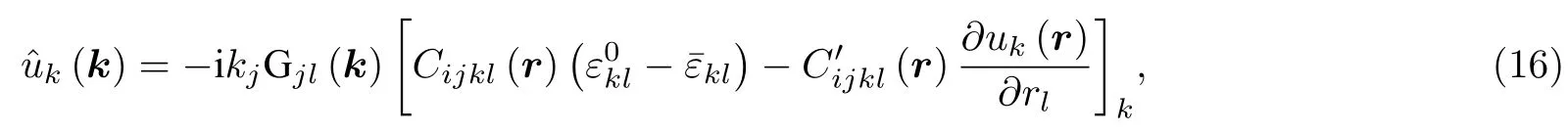
式中,k为傅里叶空间中的波矢量,Gjl(k)为格林张量.通过摄动迭代法求解(16)式,得到第n次迭代中的位移场如下[26]:

2.2 相场方程演化

对于平衡态的空洞和晶粒结构,与位置有关的弹性模量只需要通过 (4) 式计算一次,然而对于一个不断演化的含空洞的多晶体系,在每个时间步长和空间位置都要对其进行计算.考虑弹性能量贡献时,修正后的Allen-Cahn方程和Cahn-Hilliard方程如下[29]:

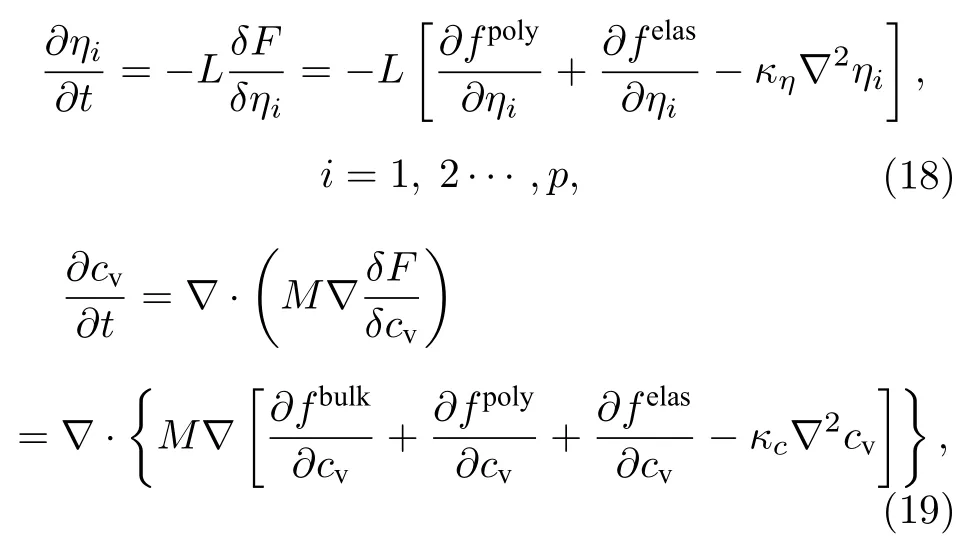
式中,t为时间;L和M为动力学参数,迁移率M表达式为MDvVm/(RT),其中Dv为空位的扩散系数;Vm为摩尔体积;R为理想气体常数.与位置相关的弹性能的表达式如下:

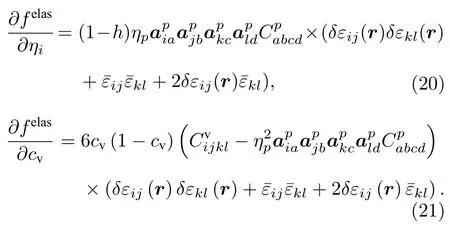
使用修正的空洞演化和晶粒生长的控制方程可以模拟多晶材料在外加应力下的组织演化过程.本文基于傅里叶谱方法编写程序对上述模型进行求解,傅里叶谱方法可以把函数的求导运算转化为相对简单的代数运算,在求解弹性平衡方程方面有独到的优势.因此,本文的Allen-Cahn方程和Cahn-Hilliard方程的求解采用半隐式傅里叶谱方法(semiimplicit Fourier spectral method):假设时间间隔为 Δt,步长为n+1的相场变量需要第n步的结果进行求解[30]:

式中,f为体自由能密度,是多晶自由能密度和弹性自由能密度的总和;k(k1,k2) 为傅里叶向量.本模拟中使用的边界条件均为周期性边界条件.空间坐标,其大小满足

2.3 参数无量纲化

模拟使用的UO2参数如表1所列,计算中还需要对参数进行无量纲化处理.本工作中,选取参考长度l∗1nm 与参考时间t∗0.03s,由此获得无量纲长度xl/l∗;无量纲时间τt/t∗;无量纲扩散系数;无量纲梯度算子其中l和t为实际长度和实际时间.无量纲化后的控制方程如下所示:

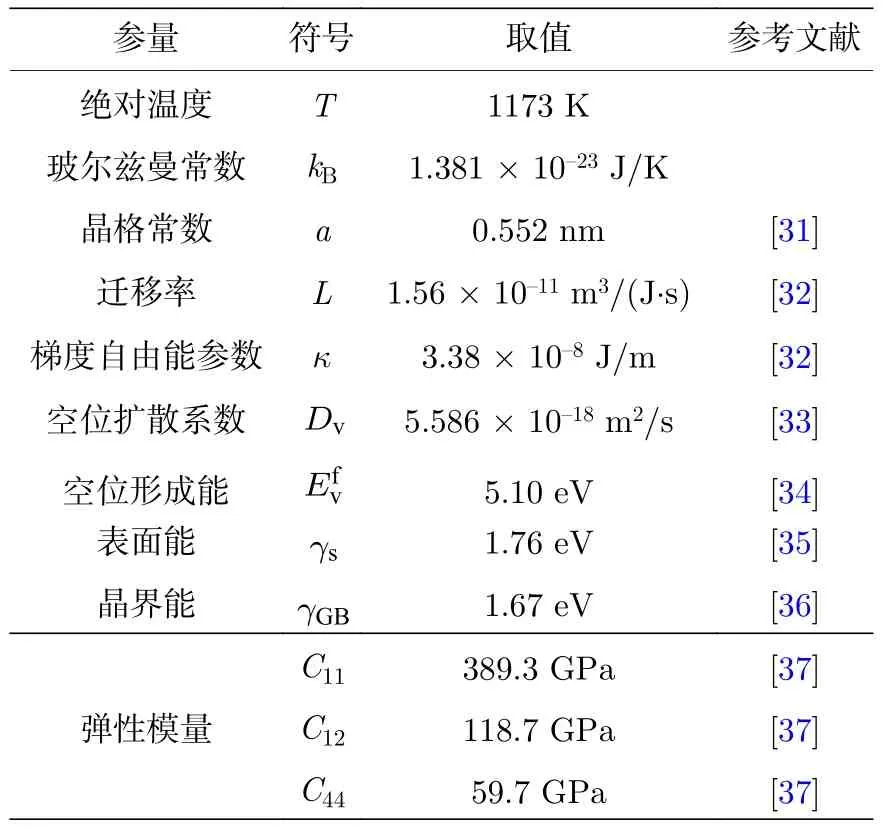
表1 模拟中使用的UO2参数Table 1.Parameters of UO2 used in the simulation.

3 结果与讨论

3.1 单个空洞应力分析

模拟中选取的空间网格为128 nm×128 nm,在模拟区域中心放入一个半径为6 nm的空洞(见图1(a)).在模拟中使用弹性各向异性的UO2弹性模量,基体中取C11389.3GPa,C12118.7GPa和C4459.7GPa (见表1),空洞相的弹性模量为10–4.此外,给模拟区域的水平方向和垂直方向同时施加100 MPa的外加应力,求解弹性方程组得到的空洞周围应力分布如图1(b)所示.由图1(b)可见,应力集中在空洞的左右边缘,这类似于有孔平面的应力集中行为,而空洞中与空洞顶部底部边缘应力较小.沿A-A,B-B和C-C截线的应力分布如图2所示,可见系统边缘处的应力与外加应力相同,而空洞边缘有应力集中的现象,这与Jin等[38]的模拟结果相似.

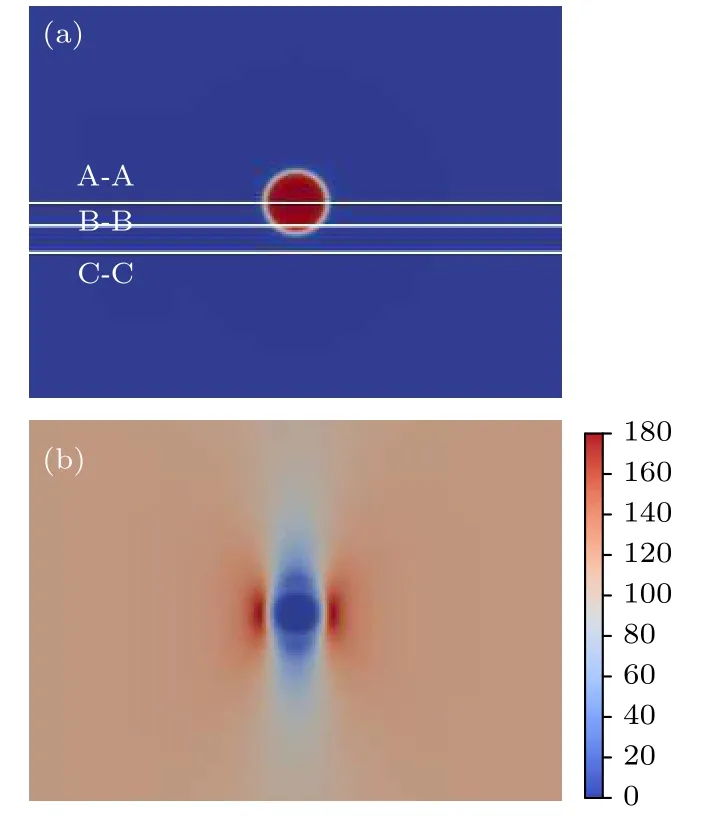
图1 (a) 初始空洞示意图;(b) 空洞周围应力分布Fig.1.(a) Schematic diagram of the initial void;(b) stress distribution with the void.

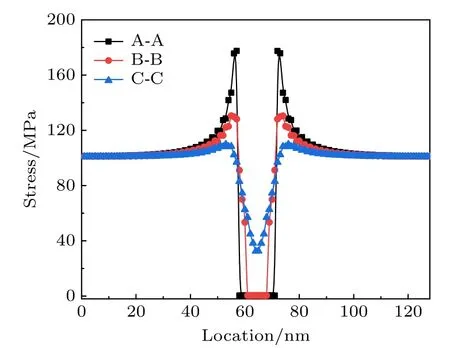
图2 三个典型截面上的应力分布Fig.2.Stress distribution along three typical cross sections.

根据弹性力学相关理论,通过设定圆孔边缘和无限远处应力的固定边界条件求解应力平衡方程,得到外加载荷下圆孔周围应力分布的解析解如下[39]:

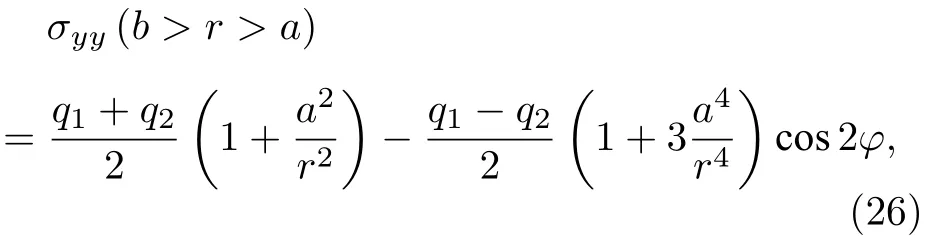
其中,q1和q2为沿x轴和沿y轴的外加应力;a为空洞半径;b为空洞中心到系统边缘的距离,计算中假设b≫a.为了对相场方法和解析解获得的应力场分布进行定量的比较,图3给出了A-A截线处模拟和分析得到的应力分布,其中黑色点线为模拟得到的数值解,红色为解析解的计算值,通过对比发现,本文的数值模拟结果与解析解符合得较好.

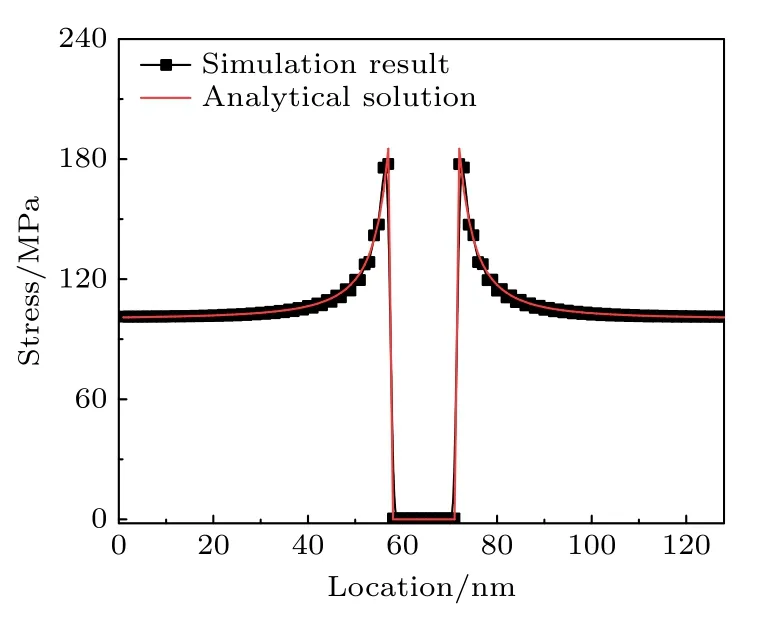
图3 模拟结果与解析解的应力分布比较Fig.3.Comparison of stress distribution between simulation results and analytical solutions.

3.2 应力条件下空洞长大

辐照条件下,基体中的点缺陷浓度处于过饱和状态,空洞通过不断吸收基体中的空位而持续生长.外加应力加速空洞肿胀主要表现在两个方面:一方面,外加应力会缩短空洞形成的孕育期,加速空洞形核;另一方面,外加应力会加速空位的迁移,从而加速空洞长大.

本工作使用相场方法对单个空洞的生长进行模拟,模拟中选取的空间网格为128 nm×128 nm,模拟区域的中心放入一个半径为6 nm的初始空洞,假设基体中的空位浓度为0.1,此时空洞处于过饱和的空位浓度中,在化学势的驱动下,空位会自发的扩散至空洞中导致空洞自发长大.

无应力下,不同模拟时间的空洞形貌如图4(a)—(c)所示.可以看出,位于模拟区域中心的空洞通过吸收周围的空位不断长大,而且在界面能的影响下,空洞在演化过程中会始终保持圆形.给模拟区域的水平和垂直方向同时施加100 MPa的外加应力,空洞随时间的演化如图4(d)—(f)所示.可以看出,相同的模拟时间下,应力作用下的空洞比无应力的空洞尺寸更大.此外,在应力作用下,空洞演化过程中也始终保持圆形.这是由于水平应力分布和垂直应力分布是沿x-y轴对称的(见图4(g)—(i)),所以空洞的形状并不会发生明显变化,如果只有一个方向的外加应力,那么空洞会沿该应力方向生长,这与Wang等[40]的结果一致.

图4 (a)−(c)无应力下空洞演化;(d)−(f) 100 MPa附加应力下空洞演化;(g)−(i)应力分布随时间演化Fig.4.(a)−(c) The evolution of void without stress;(d)−(f) the evolution of void with 100 MPa applied stress;(g)−(i) the distribution of stress during the evolution.

不同外加应力条件下空洞半径随时间的变化曲线如图5所示.由图5可以看出,在没有外加应力时,模拟结束后,空洞的半径从初始的6.0 nm增长到12.9 nm,而在50 MPa外加应力下空洞会增长到14.2 nm,在100 MPa下则增长到15.1 nm.可见,随着外加应力的增大,空洞的生长速度也会增加.不同外加应力下模拟区域中线上的应力和弹性能密度分布如图6所示.由图6(a)可以看出,空洞两端有明显的应力集中现象,而且外加应力越大,该现象越明显.由图6(b)可以看出,外加应力会使基体中的弹性能密度增大,空洞边缘还会出现弹性能升高的现象,这促进了基体相向空洞相的转变,降低了相变的能量势垒.因此,应力加速空洞肿胀的原因是外加应力影响了空洞周围的自由能密度,从而加速了空洞的生长.

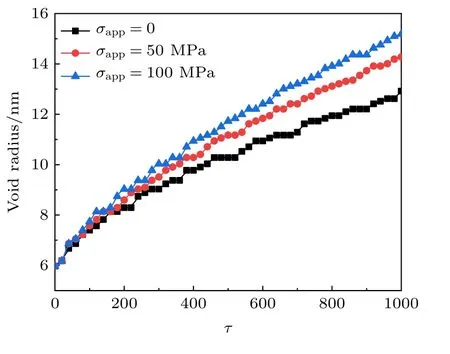
图5 不同应力下空洞半径随时间变化Fig.5.The change of void radius with time under different stresses.

图6 (a)中线应力分布;(b)中线弹性能密度分布Fig.6.(a) Stress distribution in the center line;(b) elastic energy density distribution in the center line.

3.3 应力作用下双晶系统的演化

本工作引入了一个带有晶间空洞的双晶结构,并把基体中的空位浓度设置为平衡浓度.如图7(a)所示,模拟区域中心的红色区域为空洞,左边区域为晶粒1,右边区域为晶粒2.引入一个可视化变量Φ,表达式为:

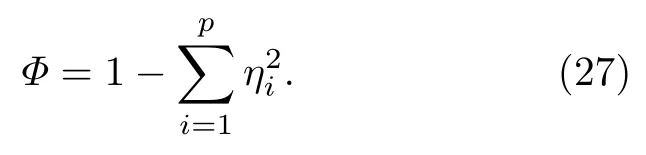
在晶粒内部Φ0,在扩散界面处 0<Φ<1,在空洞内部Φ1.0.假设晶粒1的欧拉角为θ10,晶粒2的欧拉角为θ230°.对于弹性各向异性晶粒,两个晶粒的欧拉角不同直接导致了它们的弹性模量不同[41].图7(b)为系统中线上的弹性模量分布,其弹性模量可根据(8)式计算得到.

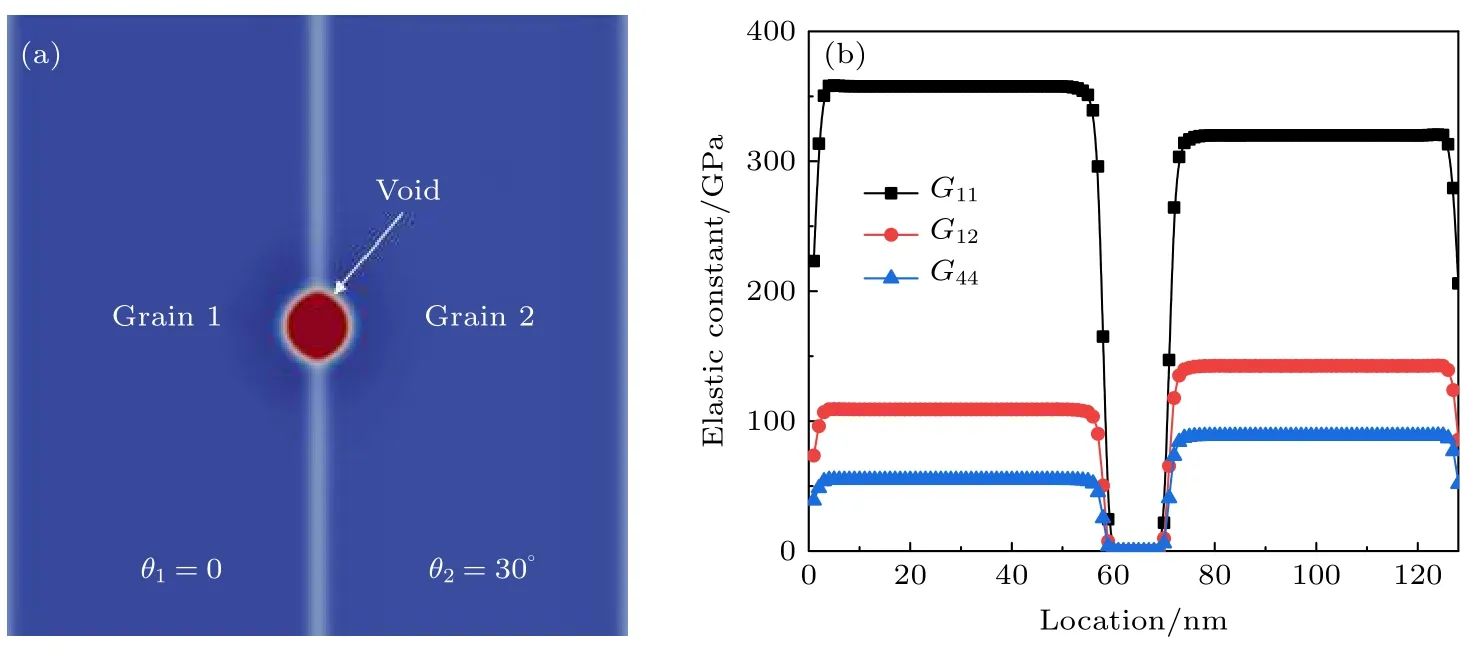
图7 (a)初始结构示意图;(b)模拟区域的水平中线上的弹性模量分布Fig.7.(a) Schematic of initial structure;(b) elastic constants distribution in the center line.

图8(a)—(c)绘制了在100 MPa的外加应力作用下,空洞和晶粒的演化过程.可以看出,晶间空洞的形状自发地演化成椭圆形,该椭圆的二面角φ由晶界能和空洞表面能共同决定,cos(φ/2)γGB/(2γs)[42],其中γGB为基体晶界能,γs为空洞表面能.此外,不同的晶粒取向对应着不同的弹性模量,从而具有不同的应力,而在应力的驱动下,晶界会不断迁移.

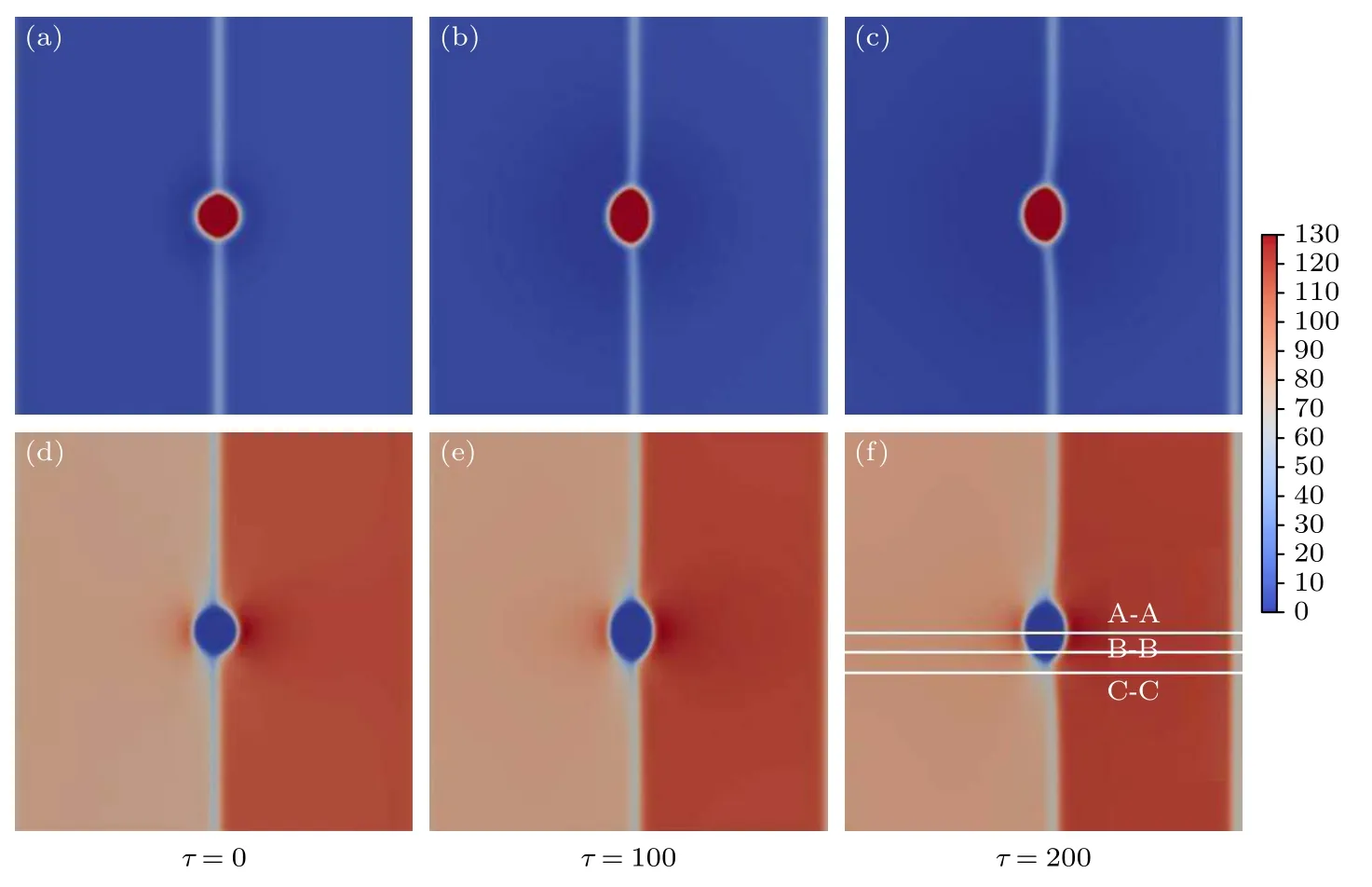
图8 (a)−(c)晶粒和空洞随时间演化;(d)−(f)演化过程中的应力分布Fig.8.(a)−(c) Evolution of grains and void with time;(d)−(f) the distribution of stress during the evolution.

双晶体系演化过程中的应力分布如图8(d)—(f)所示.可以看出,除了空洞边缘的应力集中外,晶粒内也有相应的应力分布.其中晶粒2的面积随模拟时间的延长而不断减少,这是因为晶粒2内存在更高的应力,对应的弹性能也高.此外,晶界迁移过程中会受到空洞的钉扎作用,靠近空洞位置的平直晶界会发生弯曲,迁移速度也会减缓[43].

晶间空洞演化过程中图8(f)的三个典型截面处的应力分布如图9所示.由C-C截线应力分布可知,在没有空洞影响下的应力分布有两个极小值,都出现在晶界位置,这是由于晶界处的弹性模量小于晶内的弹性模量.有空洞影响时的应力分布也有两个极小值,在空洞和晶界处,对应于图7(b)中弹性模量的极小值,而且空洞边缘处也存在应力集中现象.

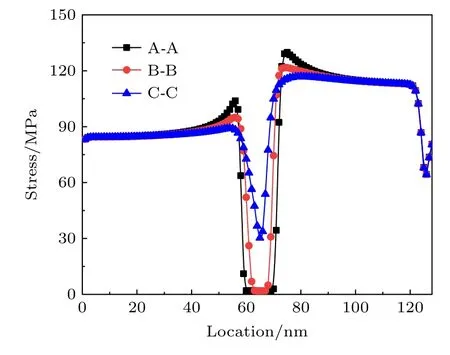
图9 晶间空洞演化中三个典型截面上应力分布Fig.9.Stress distribution along three typical cross sections during intergranular void evolution.

为研究UO2燃料中不同应力下弯曲晶界和空洞的相互作用,对图10的双晶系统进行了研究.图10中深蓝色的区域为晶粒1,浅蓝色的区域为晶粒2,两个晶粒接触的圆环为晶界,红色的区域为随机分布的不同尺寸的空洞.模拟前,基体中过饱和的空位浓度设置为cv0.1,图10为无应力条件下的微观组织演变结果.由图10可以看到,晶界处的空洞变为椭圆形,而椭圆形空洞在晶界两侧部分的曲率明显不同.

图10 无外加应力下的双晶组织Fig.10.The twin-crystal microstructure without applied stress.

在不同外加应力条件下,晶界和气孔的形貌演化结果如图11(a)—(c)所示,相应的应力分布如图11(d)—(f)所示.通过对比可以看出,随着外加应力的增加,空洞尺寸明显增加,而且外加应力还加速了晶界的移动.当外加应力为150 MPa时,晶界在相邻两个气孔之间的部分变得平直.一方面,弯曲的晶界由于曲率驱动会向着曲率中心移动,另一方面晶界处的空洞对移动晶界有钉扎作用.晶界上的气孔也会演化为透镜状而不是球形,这将有利于降低晶界和空洞自由表面的能量.此外,晶内空洞也会生长,但是靠近晶界的空洞尺寸较小,因为晶界附近的空位优先被晶界吸收,这与实验中观察的结果类似[44].

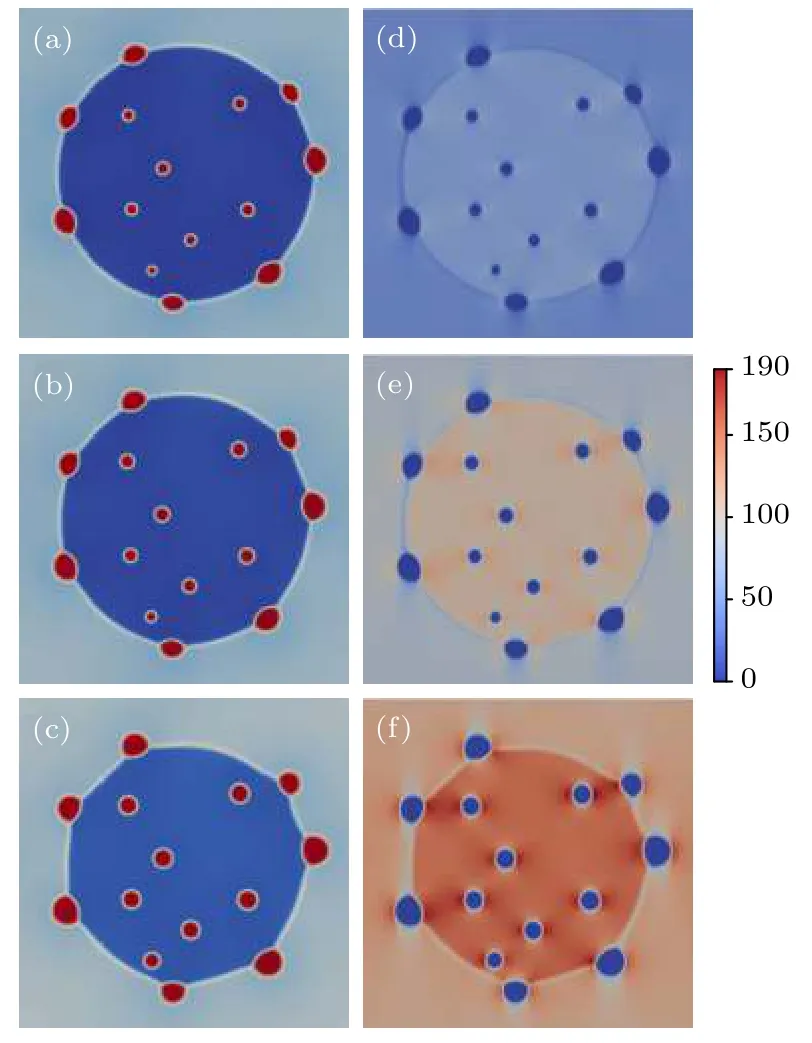
图11 不同外加应力下的双晶组织((a)—(c))及对应的应力分布((d)—(f)) (a),(d) 50 MPa;(b),(e) 100 MPa;(c),(f) 150 MPaFig.11.The twin-crystal microstructure ((a)–(c)) and the corresponding stress distribution with different applied stresses ((d)–(f)):(a),(d) 50 MPa;(b),(e) 100 MPa;(c),(f) 150 MPa.

3.4 应力作用下多晶体系的演化

模拟使用的网格为512 nm×512 nm,采用周期性边界条件并引入取向随机的26个晶粒作为初始组织,其平均尺寸为0.1 µm.同时在晶界附近和基体中随机引入多个不同尺寸的空洞.基体中的过饱和的空位浓度设置为cv0.1,无应力状态下的微观组织结构如图12所示.

图12 无外加应力下的多晶组织Fig.12.The polycrystal microstructure without applied stress.

在不同外加应力条件下,晶界和气孔的形貌演化如图13(a)—(c)所示,对应的应力分布如图13(d)—(f)所示.由图13可以看出,随着附加应力的增大,晶界和晶内的空洞尺寸均明显增加,这很可能是由于应力驱动的空洞对周围空位的吸收所引起的.此外,晶内的空洞的尺寸要小于晶间空洞.这是因为晶界作为点缺陷的吸收阱,大量空位被晶间空洞优先吸收,而且晶界处的空洞有着更小的自由能密度,有利于晶间空洞的形成和生长,这与Millett的研究结果类似[14].

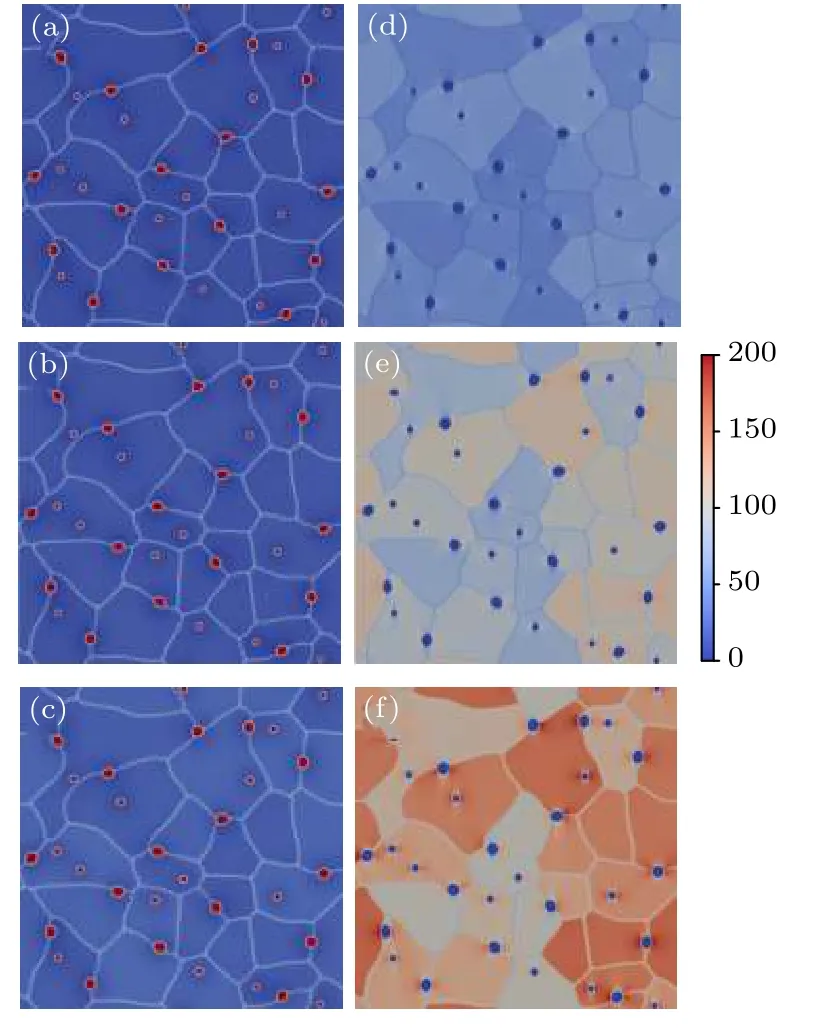
图13 不同外加应力下的多晶组织((a)—(c))和对应的应力分布((d)—(f)) (a),(d) 50 MPa;(b),(e) 100 MPa;(c),(f) 150 MPaFig.13.The polycrystal microstructure ((a)–(c)) and the corresponding stress distribution with different applied stresses ((d)–(f)):(a),(d) 50 MPa;(b),(e) 100 MPa;(c),(f) 150 MPa.

在不同外加应力下平均空洞半径的变化曲线如图14所示.由图14可以看出,平均空洞半径随着外加应力的增加而明显增加.当外加应力增加到150 MPa时,平均空洞半径从6.17 nm增长到6.96 nm左右.

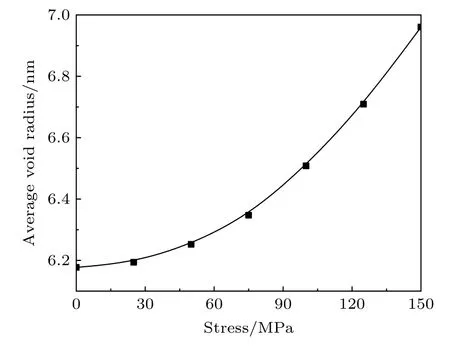
图14 平均空洞半径随外加应力变化Fig.14.The change of applied stress on average void radius.

4 结论

1)建立了外加应力作用下多晶UO2中空洞和晶粒演化的相场模型.通过摄动迭代法求解应力平衡方程,并对单个空洞周围的应力分布进行了计算,结果发现空洞边缘存在应力集中的现象.模拟得到的应力分布与平面应力分布的解析解基本符合.

2) 空洞会通过吸收周围的过饱和空位自发生长.通过计算产生的弹性能,得到了不同应力下的空洞生长规律,发现随着外加应力的增加,空洞生长的速率也增加.通过计算不同外加应力下的应力分布和弹性能密度分布,发现应力越大应力集中现象越明显,而且空洞边缘处的自由能密度越高.

3) 模型应用于含有晶间空洞的多晶体系,通过引入与晶粒取向相关的各向异性的弹性能,计算模拟了晶粒内的应力分布,结果表明,不同晶粒内的应力大小不同,且该应力会驱动晶粒演化.晶间空洞与晶界存在相互作用,一方面空洞在晶粒的影响下会生长成透镜状,另一方面空洞对晶界移动有钉扎作用,会减缓晶界的迁移.此外,外加应力会加速多晶系统中的空洞生长.外加应力越大,空洞长大越快.