基于支持向量机与改进分水岭的红细胞识别算法研究
刘生富, 张鹏程, 周广宇, 刘 祎, 桂志国
(中北大学 生物医学成像与影像大数据山西重点实验室, 山西 太原 030051)
0 引 言
随着计算机软硬件和图像处理技术的快速发展, 在医学领域中将计算机和图像处理结合起来, 能够为医务工作者提供有效的服务, 为疾病的诊断提供有力的依据. 传统红细胞计数人员手工进行计数, 统计红细胞的数量. 但是, 手动计数受个人主观意识与外界环境因素的影响, 错检率较高.
由于显微图像中细胞分布疏密程度不同、 排列状态不一、 部分细胞相互重叠、 且图像中混入杂质较多, 这些因素都给红细胞的识别带来了很大的困扰.
现有的红细胞图像自动分割方法主要包括: 阈值分割算法[1]、 分水岭算法[2]和凹点检测法[3]等. 其中阈值分割算法[1]是基于图像的灰度特征来计算一个或多个灰度阈值, 并将图像中每个像素的灰度值与阈值作比较, 最后将像素根据比较结果分到合适的类别中. 该方法计算简单, 效率较高. 但是, 该方法只考虑像素点本身灰度值的特征, 不考虑空间特征, 形状特征, 因此识别结果对噪声比较敏感, 鲁棒性较差, 无法区分重叠细胞与杂质; 分水岭算法[2]的优点是计算速度快, 能够检测重叠细胞. 但是该方法存在一个很大的缺陷, 即对图像灰度变化极敏感. 当图像的灰度分布不均时, 该方法极易造成过分割, 对于形状类似于细胞的杂质无法进行准确识别. 例如, 韩悬等人[4]提出改进的分水岭算法在图像分割中的应用, 利用Otsu[5]阈值分割法和灰度调整对图像进行前景标记, 通过距离变换的分水岭来实现背景标记, 对梯度幅值图像利用相关函数进行修改, 使其只在标记位置有局部极小值, 随后进行分水岭变换, 得出分割结果, 其结果可以将部分重叠细胞分割开. 但是对于复杂图像即前景背景灰度值相差不大的区域难以进行标记, 容易造成分割混乱, 故导致最后细胞的计数不准确; 凹点检测法[3]不依赖于显微图像的灰度信息, 仅通过分析细胞轮廓的形状和凹凸性来达到分离重叠细胞的目的. 同样该方法对非细胞的杂质难以区分开来, 并且凹点匹配有时会出现匹配错误, 即非粘连细胞的凹点进行了匹配. 例如廖苗等[6]提出的基于SVM[7-8]的椭圆拟合凹点检测细胞分割算法, 将原始图像进行二值化, 提取每个连通区域的多个形状特征并应用SVM进行测试, 区分单个与重叠细胞. 运用瓶颈检测, 寻找分离点对重叠细胞的分割. 基于细胞的椭圆或圆形结构, 对分割后的边缘, 应用改进的椭圆拟合法进行修正, 修正后的细胞区域能够反映重叠在一起的细胞的形状, 该方法只对重叠细胞进行了分离, 但是无法识别形状类似于细胞的杂质, 使得最后计数的结果会产生较大的误差.
针对以上现有红细胞识别算法存在的不足, 即重叠细胞的过分割和欠分割, 无法区分细胞与杂质, 本文提出了一种基于SVM方法和改进分水岭算法的红细胞自动识别方法. 通过提取二值化图像中细胞连通区域的多个形状特征[9-10], 利用SVM对该区域进行判断. 对于被判定为重叠的区域应用分水岭的方法将其分割为单个的连通区域. 将单个的连通区域映射到原始图像之中, 提取其颜色特征[11]之后对单个的连通区域应用另一个SVM分类器进行杂质与细胞的识别, 最后统计单个细胞的个数[12]便得到了最后的结果.
1 算法描述
本文算法流程如图 1 所示, 主要包括二值化处理、 SVM识别单连通区域与重叠连通区域、 分水岭分割重叠连通区域、 SVM识别细胞与杂质和统计计数5个步骤.
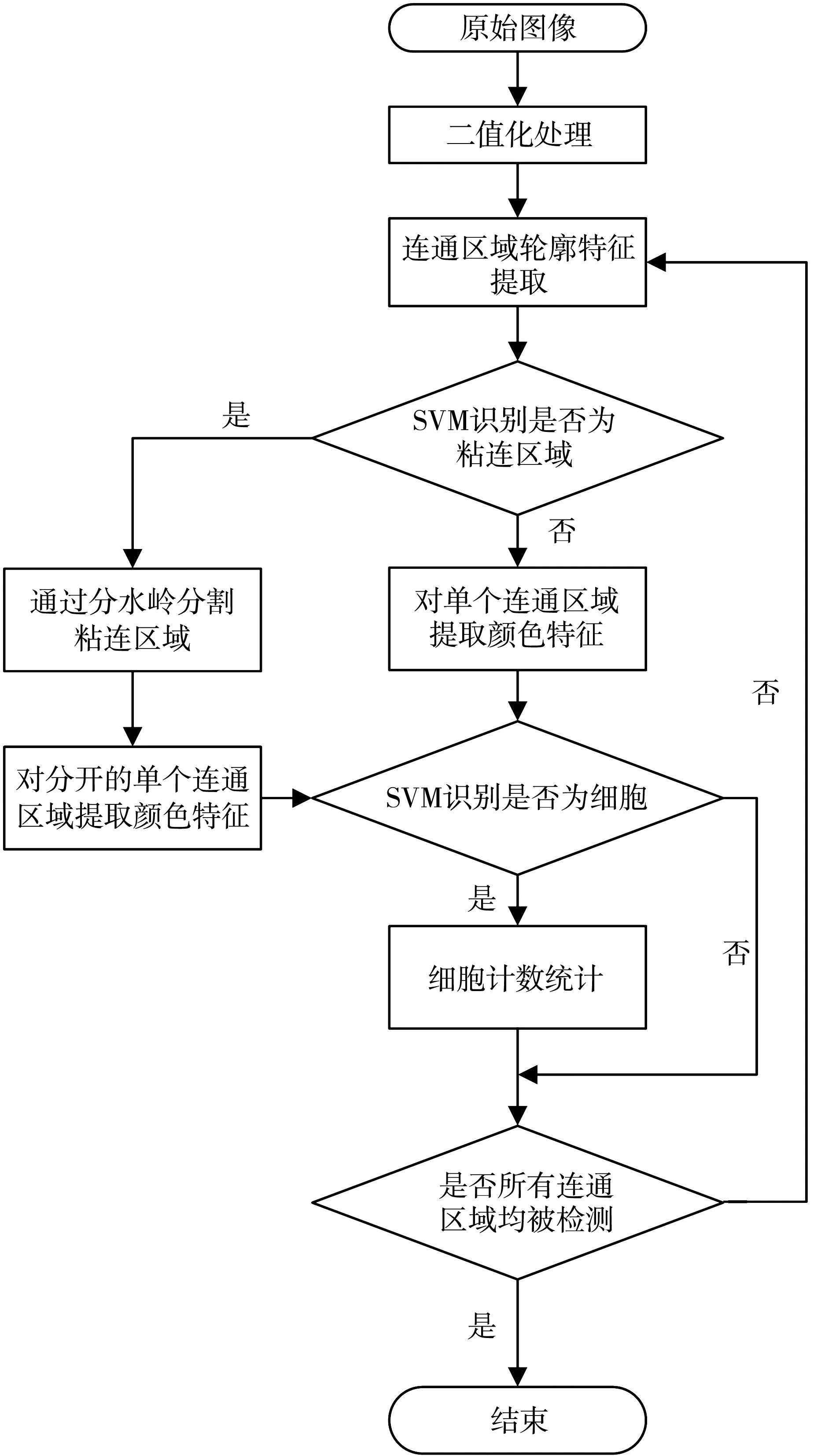
图 1 计数算法流程图Fig.1 Counting algorithm flow chart
首先, 对图像进行二值化处理, 获取细胞的黑白图像; 然后, 通过SVM分类器对二值化图像中的连通区域进行判断, 如果是粘连区域, 通过分水岭算法将粘连的连通区域分割为单个的连通区域, 接着使用另一个SVM分类器单个连通区域进行单个细胞与杂质的识别; 最后, 统计单个细胞的个数. 每个步骤的原理及实现过程见下文所述.
1.1 图像二值化
首先, 针对采集图像光照不均匀的问题, 对输入图像用基于二维Gamma函数的自适应校正算法[13], 对输入图像进行背景校正. 使用二维Gamma函数对HSV空间的V(亮度)分量进行亮度改变, 对校正后的图像进行灰度转换. 由于转换后灰度图中的背景与目标前景对比度不大, 所以采用Laplacian算子的图像边缘增强算法[14]对灰度图像进行边缘增强. 由于灰度图像存在噪声, 所以, 对其进行中值滤波降噪. 接着使用自适应阈值算法对降噪后的图像进行二值化分割. 由于红细胞自身特性呈凹饼状, 故二值化处理后图像的前景细胞存在一些空洞. 为了使前景连通区域都成为实心的闭合区域, 首先, 进行形态学[15]膨胀操作, 使二值化图像中每个轮廓都成为闭合的区域; 之后, 对二值化图像进行种子填充, 将闭合区域的内部填充为前景色. 种子填充的原理如下: 假设二值化图像为A, 首先A向外延展一到两个像素, 确保下文所提到的种子点位于背景之内, 并将值填充为背景色像素为0, 标记为B, 使用漫水填充将B的大背景填充, 填充值为前景色像素为255, 种子点为(0, 0)记为C, 将填充好的图像裁剪为原图像大小, 即将延展部分去掉, 此时图像记为D, 将D取反与A相加即得填充的图像. 至此, 轮廓都成为闭合连续的区域, 最后, 进行形态学腐蚀, 结果如图 2 所示.

图 2 原图与二值化图像Fig.2 Original image and binarization image
1.2 特征提取与分类
本文重点提取连通区域的形状特征, 细胞与杂质的颜色特征. 重叠连通区域与单个连通区域通常在形状上具有显著差异, 通过连通区域的形状特征对该区域使用SVM进行单个连通区域与重叠区域的分类. 细胞与杂质在颜色上也具有显著差异, 所以, 通过SVM进行细胞与杂质的分类. 分类结果的好坏很大程度上取决于定义的特征, 特征分类的定义如下:
特征1: 计算图像中连通区域外轮廓与其外轮廓凸包的匹配率

(1)
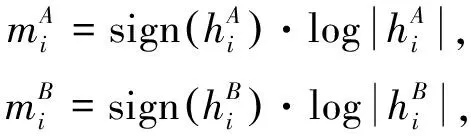
(2)

特征2: 计算图像中当前轮廓区域的矩形度
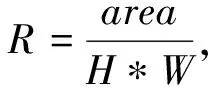
(3)
式中:area代表当前区域轮廓的面积;H*W代表外接矩形的面积, 若R的值接近于1, 则说明是单细胞; 若明显小于1, 则说明是重叠的细胞.
特征3: 计算图像中轮廓似圆度

(4)
式中:area代表当前轮廓区域面积;L代表当前轮廓的周长;C为轮廓似圆度, 单个连通区域明显接近圆形, 所以轮廓似圆度接近于1, 而重叠的区域明显偏离了1的范围.
特征4: 计算图像中轮廓拟合出的椭圆长短轴之比
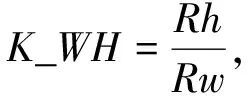
(5)
式中:Rh代表当前区域的拟合椭圆的长轴;Rw代表当前区域的拟合椭圆的短轴.若K_WH接近于1, 则为单个细胞; 若明显大于1, 则为重叠细胞.
特征5: 计算彩色图像中黑色分量占比, 计算原始图像轮廓外接矩形区域的偏黑色分量, 并以此为阈值, 直接对彩色图像进行二值化, 输入一个低值数组与一个高值数组, 每个通道的像素值都在规定的数组范围内, 则令该像素为255, 否则为0, 此时计算255像素总量与其图片区域总像素的比值.
特征6: 计算彩色图像中绿色分量占比, 原理同特征5.
特征7: 计算彩色图像中黄色分量占比, 原理同特征5.
有些杂质形状类似单个细胞, 但颜色有明显差别, 所以将黑白图像映射到彩色图像去计算3个颜色分量的占比, 从而将杂质与单个细胞区分开来, 使得计算结果更加精确. 特征1到特征4作为识别单连通区域与重叠连通区域的特征, 特征5到特征7作为识别细胞与杂质的特征. 单个细胞, 重叠细胞, 杂质如图 3 所示.

图 3 细胞的不同形态Fig.3 Different morphology of cells
1.3 重叠细胞的分水岭分割
传统的分水岭算法基于拓扑理论的数学形态学分割方法, 基本思想是把图像看作是测地学上的拓扑地貌, 图像中每一点像素的灰度值表示该点的海拔高度, 每一个局部极小值及其影响区域称为集水盆, 而集水盆的边界则形成分水岭. 该算法可以模拟成洪水淹没的过程, 图像的最低点首先被淹没, 然后水淹没整个山谷. 水位到达一定高度将会溢出, 这时在水溢出的地方修建堤坝, 直到整个图像上的点全部被淹没, 这时所建立的一系列堤坝就成为分开各个盆地的分水岭. 由于图像中灰度极小值点较多, 这就导致集水盆数目过多, 从而造成图像的过分割, 因此本文对分水岭算法进行了一些改进, 将图像分为前景区域、 背景区域和不确定区域3部分, 并对其进行标记之后进行分水岭变换, 可以有效防止过分割.
1) 通过SVM分类得到重叠的连通区域, 获取此重叠的连通区域.
2) 对获取的区域图像进行距离变换, 距离变换主要是用来细化细胞的轮廓,寻找细胞的质心,距离变换之后就得到了所需要的前景区域.
3) 通过对白色前景的深度膨胀运算获得一个超过前景实际大小的物体, 用反向阈值将深度膨胀后的图像中黑色部分转换成128像素, 即完成了对背景像素的标记.
4) 背景区域与前景区域进行合并, 便得到了标记图像, 像素为128为背景区域, 像素为255为前景区域, 像素为0则为不确定区域, 不确定区域主要含有目标图像与背景的边界点, 以及周围难以鉴别的部分.
5) 对得到标记的图像进行分水岭变换, 可以将重叠的连通区域分割开, 最后将轮廓进行椭圆拟合, 并在彩色图像上对应位置进行标注. 对图 3(a) 与图 3(b) 的分割拟合结果如图 4 所示.

图 4 分水岭算法标记与结果Fig.4 Watershed algorithm markers and results
2 实验结果与分析
本文在实验室自主开发的便携式血常规检测仪中进行图像采集, 检测卡的细胞检测孔管底内壁沉积有经过处理的红细胞溶液, 通过显微摄像机获取实验所需图像.
SVM是实现自然图像自动分类的方法, 是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法. 给定一组训练数据, 每个训练数据被标记为属于两个类别中的一个或另一个, SVM 训练算法创建一个将新的实例分配给两个类别之一的模型, 使其成为非概率二元线性分类器. SVM模型是将实例表示为空间中的点, 这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开. 之后, 将新的实例映射到同一空间, 并基于它们落在间隔的哪一侧来预测所属类别. 简言之, SVM 就是一种二类分类模型, 他的基本模型是定义在特征空间的间隔最大的线性分类器, SVM 的学习策略就是间隔最大化. 对于本实验, SVM分类器的核函数选择均为线性核. 影响SVM 分类器性能较大的参数为惩罚系数C,C越高, 越容易过拟合;C越小, 越容易欠拟合, 这里我们经过反复实验得出惩罚系数C为1的时候, 识别准确率最高.
其中SVM训练数据集采用LabelMe制作, 包括80个单个细胞的正样本1, 80个重叠细胞的正样本2, 40个杂质的负样本. 提取正样本1与正样本2的形状特征, 输入SVM1训练, 提取正样本1与负样本的颜色特征, 输入SVM2训练, 上述特征均为1, 2所定义的特征. 对于实验的测试图像, 需要提取每个连通区域的形状特征, 通过SVM1分类器去识别单连通区域与重叠连通区域, 对于重叠连通区域, 使用改进的分水岭算法分割为单个连通区域. 将单个连通区域的位置映射到原始图像的同一位置, 提取颜色特征, 通过SVM2去识别是否为细胞, 将最终识别的细胞区域进行椭圆拟合并在原始图像上进行标记.
针对图2的a, b, c 3幅图像的实验结果如图 5 所示, 将本文使用的算法与直接使用分水岭分割算法、 凹分割算法的准确率进行比较, 图 5 中的a1方框标记的部分为杂质, 本文算法将其作为杂质识别出来, 所以没有对其进行标记, 而在a2, a3方框标记的部分可以看出对杂质进行了标记, 把杂质当做细胞进行处理. 对于b1中方框标记的部分有两个杂质, 在b2与b3中错误地把这两个杂质当成细胞进行处理. 同样在c1中, 方框所标记的部分有两个为杂质, c2与c3中错误识别. 所以通过实验结果可以看到, 本文的算法可以很好地将细胞与杂质区分开. 经过本文算法处理, 图 5 中的重叠细胞可以很好地分割出来, 从而提高计数的准确率.

图 5 红细胞识别算法结果比较Fig.5 Comparison of red blood cell recognition algorithm results
本文使用的红细胞识别算法可以很好地通过颜色特征将形状相似的细胞与杂质区分开来, 准确度大幅度提升. 对100张不同血液细胞图像进行计数准确率统计, 发现血液细胞浓度越高, 计数的准确率就越低, 但是对于细胞液较高浓度的血液细胞图像, 准确率也在90%以上, 如表 1 所示. 将经本文算法处理所得红细胞的计数结果与红细胞的标准数目作比较, 识别准确率为94.3%以上, 将本文算法与其它两种算法进行比较, 可以看出本文算法的识别准确率明显优于其它算法.
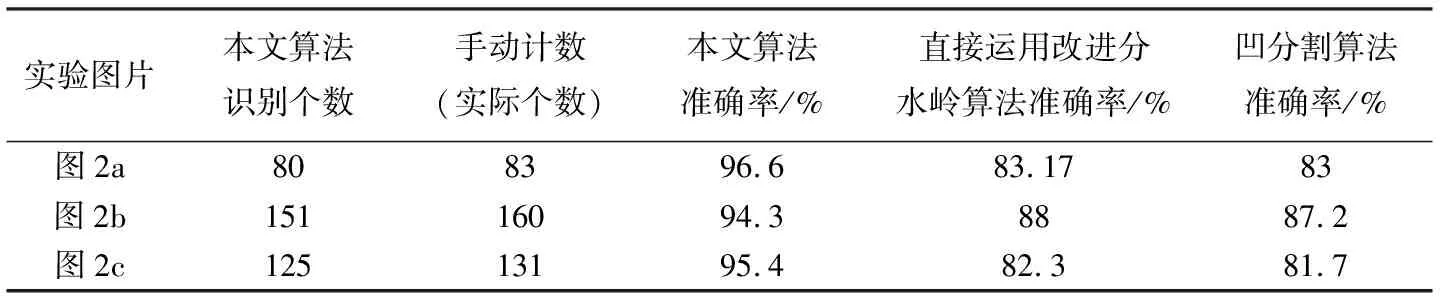
表 1 本文识别算法与其它算法的比较
3 结 论
本文提出一种基于SVM方法[16]和改进分水岭算法的红细胞图像自动识别方法. 首先对原始图像进行二值化处理, 通过提取二值化图像中连通区域的多个形状特征, 对连通区域进行判断. 对于被判定为重叠的区域, 应用改进分水岭方法将其分割为单个的连通区域, 将单个的连通区域映射到原始图像中同一位置, 提取其颜色特征之后对此连通区域应用另一个SVM分类器进行杂质与细胞的识别, 最后统计细胞的个数便得到了最后的结果, 采用椭圆拟合的方法在原图上进行标记, 以便更好地观察其结果. 经本文的算法处理, 识别准确率达到了94.3%. 结果表明, 本文算法可以很好地将重叠区域分开, 将细胞与杂质区分开, 识别准确率得到了很大的提升.

