工业园区污染废气的动态关联分析方法
朱 涛, 王晓凯, 卫晓旭, 凌德森
(山西大学 物理电子工程学院, 山西 太原 030006)
0 引 言
随着改革开放推动国民经济的发展, 工业园区逐渐建立起来, 它推动着国家工业和制造业的发展, 国家GDP的60%都是由各级各类园区占据[1]. 尽管工业园区给国家的经济带来大幅度的推动, 但是在环境污染方面却出现了很多问题. 2019 年, 全国337个地级及以上城市中, 仍有180个城市环境空气质量超标[2], 全国环境污染问题仍然严重. 如何快速地监测和追踪废气污染源头是目前环境治理的重中之重.
工业园区内企业众多, 地形复杂, 再加上天气、 风向、 季节、 压强等众多影响废气浓度分布的因素, 寻找污染因素的工作不好开展. 目前, 国内外对于环境污染治理采用的代表性方法是气体扩散模型和关联分析方法. 气体扩散模型是一种以概率模型为基础, 模拟气体扩散的模型, 以高斯烟羽模型[3]和高斯烟团模型[4]为主要代表. 张成才等[5]利用高斯扩散模型建立废气污染扩散预测系统, 模拟工业废气污染对周边空气质量的影响. 李万莉[6]通过建立改进的高斯烟羽模型, 在天然气泄漏时预测天然气的浓度分布有很好的效果. 扩散模型主要通过污染源信息得到污染物的扩散和分布, 然而在前向分析情况下, 由于假设的参数过量, 高斯模型很难反演计算, 当设置的参数不准确时, 反向模型会输出不同的推理结果. 所以, 在变量影响的推断和源头追踪方面, 扩散模型存在很大的不足.
现代工业园区废气扩散过程中会涉及到气体之间的相互作用以及气体与外界之间的相互作用, 这导致工业园区周边环境的每一种物质会因为一定的相互作用而联系在一起[7 ], 所以废气污染物关联分析方法是确定污染因素、 推理污染源头的有效方法. 目前, 关联分析屡见不鲜, 主成分分析法、 灰度关联分析法、 斯皮尔曼相关系数(Spearman)、 最大信息系数(Maximal Information Coefficient, MIC)等在各行各业都有广泛应用. Qiao Z等[8]利用偏相关和层次聚类分析方法, 首次在全国范围内探讨了空气污染指数(API)与多个气象参数之间的关系, 提出了空气质量对气象条件敏感性的时空变化见解. Spearman相关系数和最大信息系数[9]都是度量两个变量之间的统计学关联系数, 均可用于线性和非线性数据; 范秋香[10]采用Spearman相关系数, 分析了临沂市经济技术开发区4年内污染排放量的浓度分布变化, 得出O3浓度呈现显著上升趋势, 污染颗粒物PM10, PM2. 5和大气主要污染物SO2的年均值呈显著的下降趋势; 朱青等[11]通过最大信息系数等分析2014年鄱阳湖生态环境质量空间分布特征, 得出影响原始遥感生态指数(RSEI0)的关键影响因素, 为湖区环境污染治理提供了关键信息.
由于影响空气污染的不确定因素很多, 需要进行全面的关联分析, 相关分析方法层出不穷, 选用合适的相关分析方法作为本文的关联方法非常重要. 传统的关联分析只能看出废气污染物与影响因素之间的长期关联度, 无法从时间维度上分析废气污染物与其影响因素的时序特征, 并且效率差, 分析效果不佳. 关联分析不仅要做到分析准确, 还要做到高效率. 为了解决此问题, 本文重点对动态分析进行研究, 为了做到动态分析, 本文提出含自适应滑窗的动态分析方法, 配合Spearman相关系数和最大信息系数加权来分析废气污染物与各个影响因素之间的动态关联度.
1 动态关联分析总体框架
目前, 在国家环境治理的大力监督管理下, 各城市已经形成了网格化的监测系统, 像工业园区这种工业废气主要排放区内通常安装有不同位置的工业废气浓度传感器, 组成了工业污染监测站点, 环保部门通过各个站点采集数据, 监测着工业园区的环境质量. 本文通过分析某站点的数据, 采用动态关联分析方法来分析与异常污染物关联度高的其他污染物. 图 1 为动态关联分析方法总框架, 主要分为3个步骤: 数据获取、 动态关联分析和筛选异常指标和时刻.
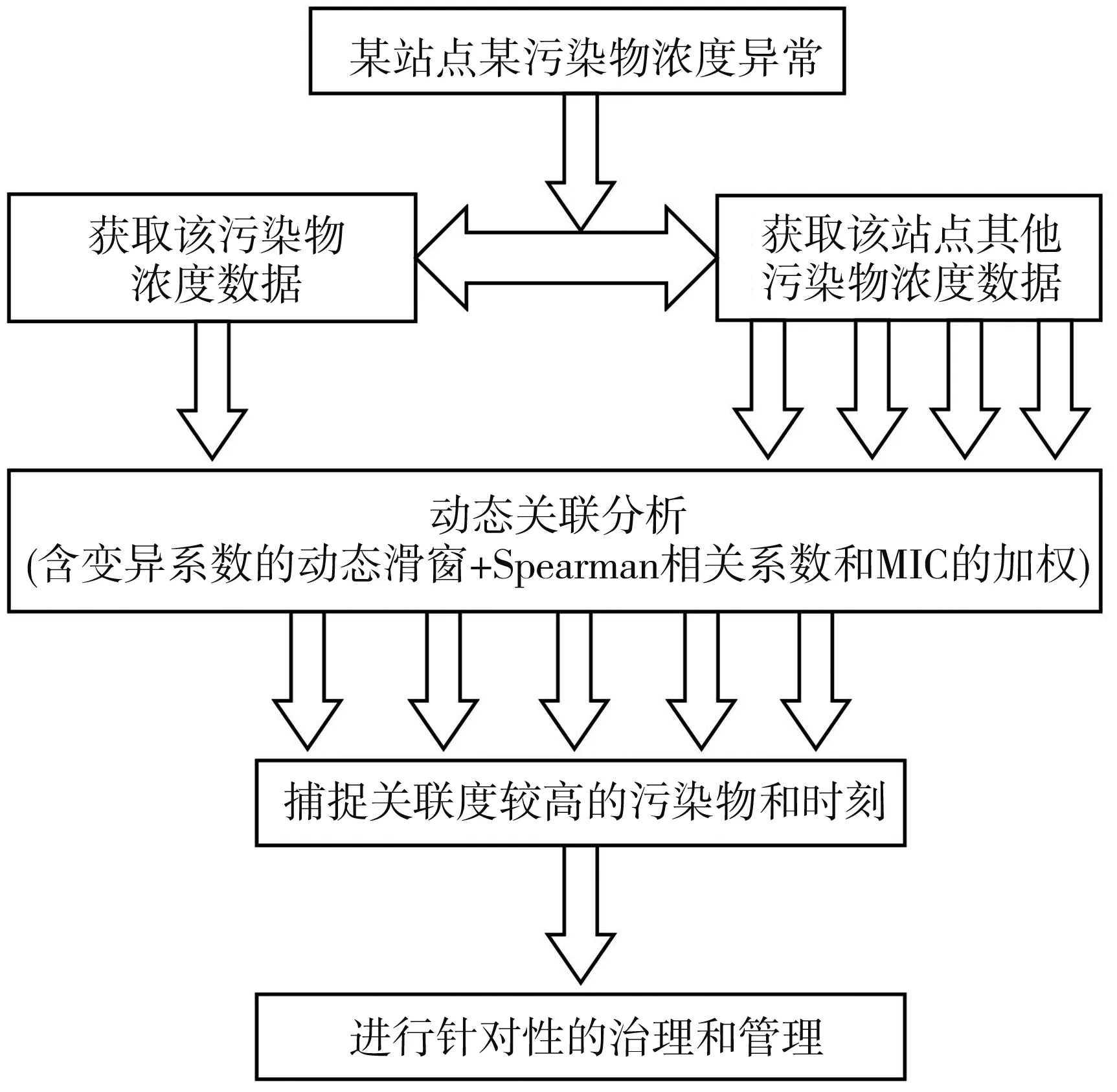
图 1 动态关联分析方法总体框架Fig.1 The general framework of dynamic correlationanalysis method
当某监测站某污染物浓度异常(工业主要废气污染物浓度数据超标或者即将超标), 获取该污染物历史浓度数据, 一般获取一个月内的历史数据, 并获取该站点其他污染物历史浓度数据; 利用含滑窗的动态关联分析方法计算目标污染物与该站点其他污染物之间的关联度, 该关联度为动态指标, 具有时序性; 通过对关联度的分析, 获取与该站点异常污染物具有高关联性的一种或几种废气污染物及其时刻; 根据分析结果对工业园区进行针对性的监督和管理.
2 动态关联分析方法
2.1 含变异系数的动态滑窗设计
变异系数是衡量数据离散大小的统计量, 它的计算方法是标准差和平均值的比值, 它可以消除量纲带来的影响[12]. 以变异系数为基础, 可以计算一段时序数据的变异系数变化率, 从而反应该段数据的波动情况, 通过设置合理的阈值来判断该段数据的波动范围, 并以反馈的形式来调整需要关联分析的数据长度.
在分析每段时间序列的关联性时, 为了加快算法效率但不丢失关键特征, 需要考虑数据的波动情况, 采用自适应滑窗的方法来处理数据, 当数据波动过于平稳时, 自适应滑窗将加长截取窗口的长度, 扩大关联分析的范围; 当数据波动过于剧烈时, 自适应滑窗将缩短截取窗口的长度, 减小关联分析的范围, 提高瞬时特性辨识度. 在此思路下, 提出基于变异系数的自适应滑窗确定方法, 具体包括以下步骤:
Step 1: 根据设置的初始窗长L0截取数据段, 并求取截取的数据段的变异系数C
(1)
式中:σ0是该段数据的标准差;m0是该段数据的平均值.
Step 2: 将该数据段再分成s段, 每段长度为L0/s;
Step 3: 求取每小段的变异系数Ci
(2)
式中:σi是第i小段数据的标准差;mi是第i小段数据的平均值.
Step 4: 求取该数据段的变异系数变化率

(3)
Step5: 滑窗长度调整比例

(4)
且

(5)
式中:kmax,kmin为稳定性判别阈值;L为更新后的窗口长度.
2.2 Spearman相关系数和最大信息系数
Spearman相关系数和最大信息系数都是度量两个变量之间的统计学关联系数, 均可用于线性和非线性数据. 而且两者计算复杂度低, 鲁棒性高, 对于样本的数量没有过多的要求, 均可以处理小样本数据, 更适用于污染废气动态关联分析方法.
2.2.1 Spearman相关系数
Spearman相关系数可以用来量度两个波形的相关程度, 取值在-1和1之间. 若两个波形在一定范围内呈正相关, 存在高度的相似性, 则取值为正值, 绝对值越高, 关联度越高; 若两个波形在一定范围内呈负相关, 波形存在相反的趋势, 则取值为负值, 绝对值越高, 负相反的程度越高. Spearman相关系数具体思想为:
将时序数据x和y分别按照升序或者降序来排列数据, 将数据x和y内的每个元素在排列中的位置记作该元素的秩次, 从而得到数据x和y的秩次数列r和e, 将数列r和数列e内每个元素对应相减得到秩次差数列d={d1,d2,…,dn}, 再将其带入斯皮尔曼相关系数公式[13]
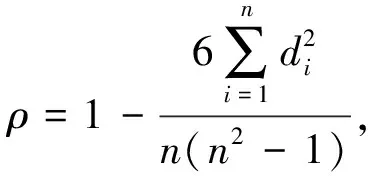
(6)
式中:n为数据样本量;ρ为斯皮尔曼相关系数;i为第i个样本.
2.2.2 最大信息系数
最大信息系数也可以用来反应两个波形之间的关联程度, 以互信息为基础, 采用网格划分的方法, 相较于互信息而言有更高的准确度, 具有普适性、 公平性和对称性. 其计算过程如下:
对于给定的数据集D={(Xi,Yi),i= 1,2,…,n}, 在直角坐标系中, 如果将X轴划分为f个格子,Y轴划分为g个格子, 可以得到一个f×g的网络划分G, 将落入G的点的数量占数据集D数量的比值看作是其概率密度D|G, 而根据不同的网格划分情况得到的概率分布D|G.变量X和Y的最大互信息为[14]
(7)
式中:D是给定的数据集;f,g是对这个数据集的某种划分数量;p(X,Y)是联合概率密度;p(X) 和p(Y)是边缘概率密度.
相同f×g的网络划分有很多种划分方式, 会得到不同大小的互信息值, 记录不同划分情况下最大的互信息值为MI(D,X,Y).之后再进行归一化, 使其取值在[0,1]之间
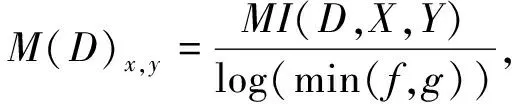
(8)
取不同网格划分下的最大的归一化后的互信息值作为最大信息系数的值. 假设样本数量为n, 最大信息系数的定义为

(9)
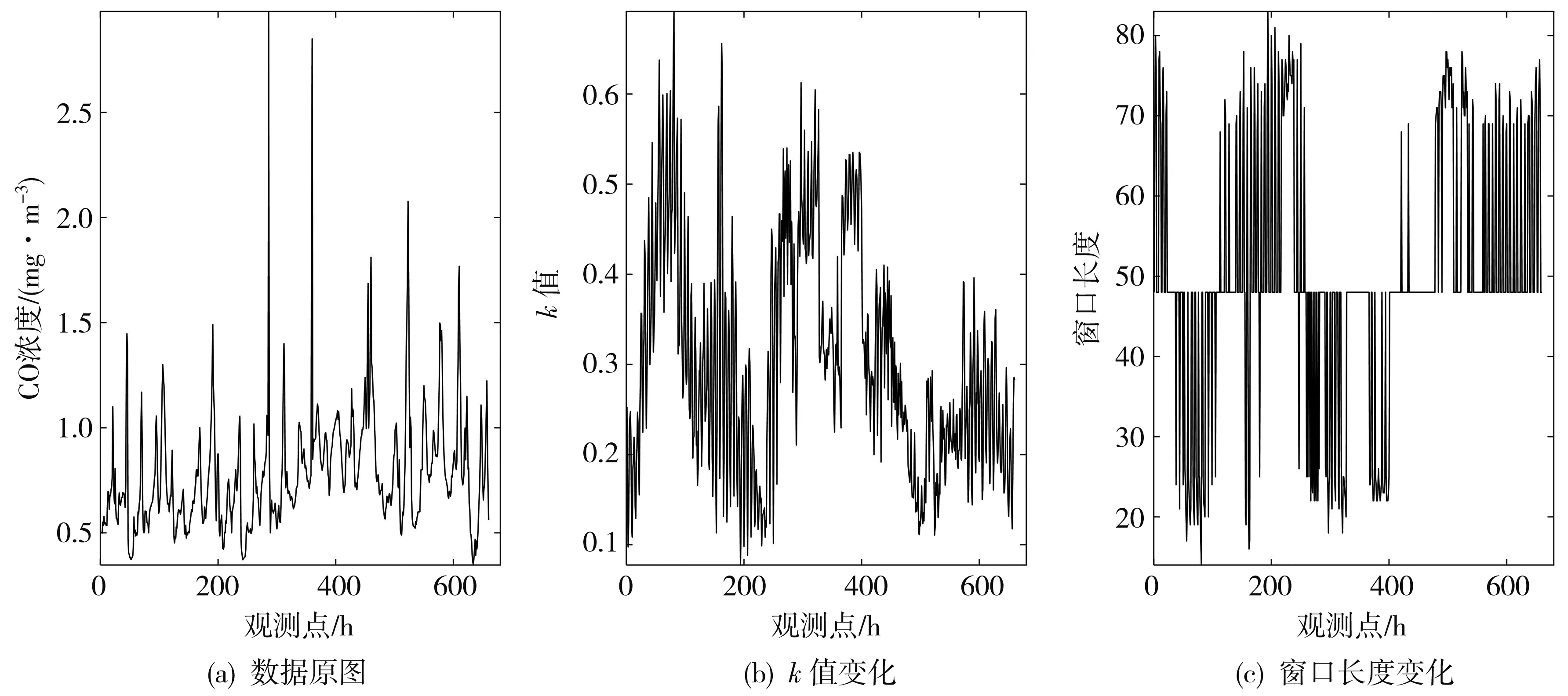
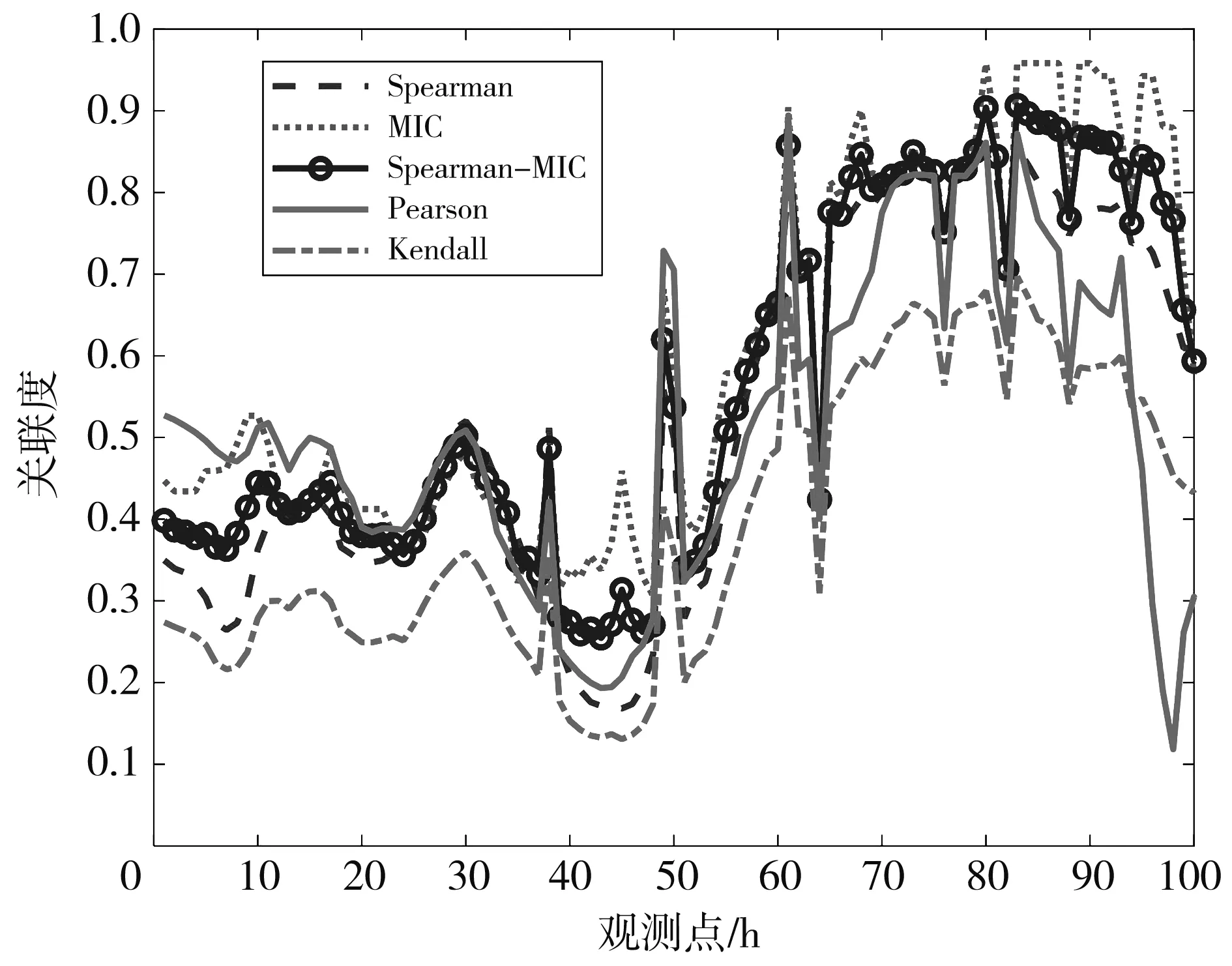
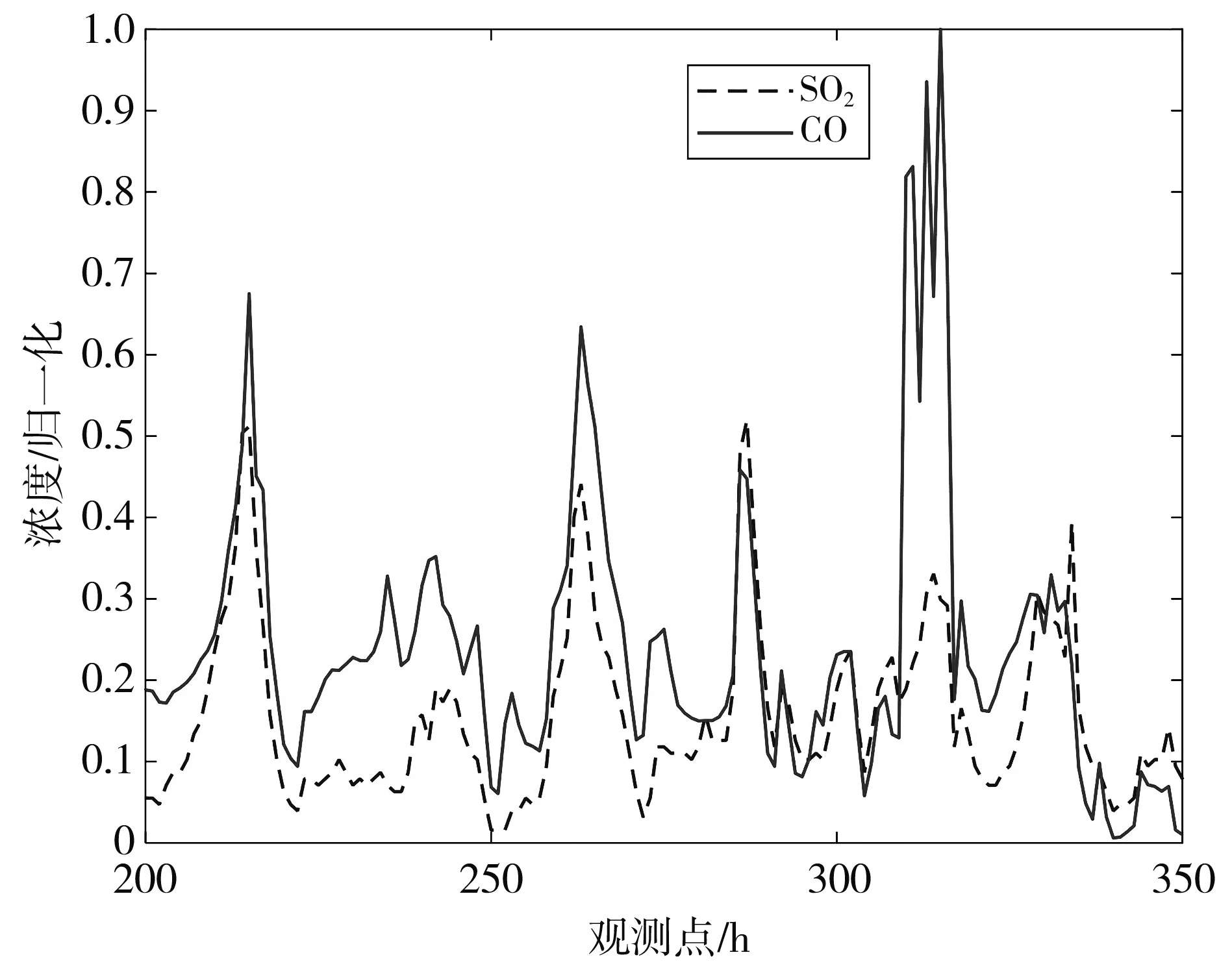
式中:fg 2.2.3 Spearman相关系数和MIC加权 Spearman相关系数和最大信息系数可以衡量数据变量之间的线性关系和非线性关系, 但是最大信息系数只能表现出两变量的某种函数关联度, 无法表征出负相关的程度, 而Spearman相关系数具备这一点, 但是Spearman相关系数的鲁棒性没有最大信息系数的高. 所以鉴于两种系数的优点, 采用Spearman相关系数和最大信息系数加权的方式作为相关方法: 当Spearman相关系数和最大信息系数都为正值时, 取两者的平均值; 当Spearman相关系数为负值时, 取两者的绝对值的平均值, 然后均值再加负号. 动态关联分析方法是一种能对时序数据在时间维度上进行动态关联分析的算法, 依靠含变异系数的动态滑窗设计, 根据数据的波动情况, 实时调整窗口的长度, 配合Spearman相关系数和最大信息系数的加权相关法, 将研究对象的长期关联度切割成若干个瞬时关联度, 反应出数据的动态特性, 工业园区污染废气动态关联分析算法流程如图 2 所示. 大致流程如下: Step 1: 获取异常污染物浓度数据和其他污染物浓度数据. 图 2 工业园区污染废气动态关联分析算法流程Fig.2 Dynamic correlation analysis algorithm flow ofindustrial park pollution exhaust gas Step 2: 截取T时刻及以前一定长度L0异常污染物历史数据,L0为初期调研实验后得出的最佳值. Step3: 通过变异系数及其变化率判断数据是否稳定, 具体判断规则如2.1节所示,kmax,kmin为初期调研实验后得出的最佳值. Step 4: 如果数据稳定, 使用Spearman相关系数和MIC加权相关方法进行关联分析; 若数据不稳定, 则通过调整规则调整滑窗长度, 然后再进行关联分析. Step 5: 判断所有数据是否全部完成动态关联分析, 没有的话, 截取T+1时刻重复step 2到step 4的步骤. Step 6: 如果数据已全部完成动态关联分析, 输出动态关联结果. 以某工业园区CO浓度数据作为本文的主要研究对象, 以2017年4月到6月的数据(时均值)作为实验数据, 其中包括SO2, NO2, CO, O3、 温度、 湿度等指标(因为示例数据是非化工园区采集的数据, 所以污染物主要以碳硫化物、 氮氧化物为主). 本文共设置3组实验, 实验1: 取2017年5月和6月的CO数据进行含变异系数的自适应滑窗实验, 数据长度为660 h, 观察数据波动情况与窗长的变化. 实验2: 取2017年6月的CO数据分别与NO2和SO2数据进行含滑窗的动态关联实验, 数据长度为 660 h, 用不同的相关方法(皮尔逊相关系数(Pearson)、 Spearman相关系数、 最大信息系数、 肯德尔系数(Kendall)、 本文中的加权相关方法)进行比较. 实验3: 以2017年4月的CO数据为研究对象, NO2, SO2为关联对象进行本文中的动态关联分析实验, 数据长度为660 h(时间尺度约为1个月), 初始窗长L0均设置为48 h,kmax设置为0.45,kmin设置为0.2,s设置为 8 h. 取2017年5月和6月的CO数据进行含变异系数的动态滑窗实验, 观察数据波动情况与窗长的变化. 2017年5月的CO数据定义为数据1, 2017年6月的CO数据定义为数据2. 图 3 为数据1数据波动情况和窗口长度变化情况, 图 4 为数据2数据波动情况和窗口长度变化情况. 图 3 窗口变化情况(数据1) 图 4 窗口变化情况(数据2)Fig.4 Window changes (data 2) 图 3(a)和图4(a)为CO数据原图, 图3(b)和图4(b)为2.1节介绍的滑动窗口调整比例k值的变化, 图3(c)和图4(c)为更新后窗口长度的变化. 由图可知在数据波动较大的区域, 窗口可以及时地变小, 在数据相对平稳的区域, 窗口可以适当的变大. 数据1相较于数据2比较平稳, 数据2中CO浓度最高峰值达到3 mg/m3, 相应的数据1的窗口长度加长的时刻比较多, 数据2的窗口长度缩短的时刻比较多. 取2017年6月的CO浓度数据分别与NO2和SO2浓度数据进行含滑窗的动态关联实验, 为了方便观察只截取前100 h, 用不同的相关方法(Pearson系数、 Spearman相关系数、 MIC、 Kendall系数、 本文中的加权相关方法(Spearman-MIC))进行比较. 图 5 为CO浓度与NO2浓度的动态关联分析, 图 6 为CO浓度与SO2浓度的动态关联分析, 从图中可以看出Pearson系数忽高忽低, Kendall系数普遍偏低, 本文中的Spearman相关系数和MIC加权的相关方法始终处于中间的位置, 更能准确地表征两变量的关联特征. 图 5 CO-NO2关联度Fig.5 CO-NO2 correlation degree 图 6 CO-SO2关联度Fig.6 CO-SO2 correlation degree 以2017年4月的CO数据为研究对象, NO2, SO2为关联对象进行本文中的动态关联分析实验. 图 7、 图 9 分别展示了CO与NO2, SO2的动态关联分析结果. 并且展示了CO与这两种不同污染物的长期静态关联度. 两个不同的指标都有较为突出的高关联时间段, 说明此时此刻该指标对于CO浓度有着较大的影响. 图7中大约有7个以上峰值超过0.8, 观测点550往后有着较高的关联度, 说明这些时刻CO和NO2关系密切, 在图9中大部分的区域都在长期关联度以上, 说明CO浓度和SO2有着很大的关系. 图 8、 图10分别展示了高关联度时间段内, CO与NO2, SO2的波形变化图(因不同污染物数据量纲不同, 为了方便观察故作归一化处理). 通过波形图可以看出, 当NO2浓度和SO2浓度升高后, CO浓度也随之升高. 根据这些信息进行污染的专项防治, 为CO浓度异常提供了关键信息. 图 7 CO与NO2动态关联度Fig.7 Dynamic correlation degree between CO and NO2 图 8 CO与NO2高关联度区间波形变化Fig.8 Variation of high correlation interval waveformbetween CO and NO2 图 9 CO与SO2动态关联度Fig.9 Dynamic correlation degree between CO and SO2 图 10 CO与SO2高关联度区间波形变化Fig.10 Variation of high correlation interval waveformbetween CO and SO 针对工业园区废气污染治理问题, 本文基于变异系数的动态滑窗提出了一种动态关联分析方法. 该方法使用变异系数及其变化率判断数据段波动性自适应地调整窗口大小, 借助Spearman相关系数和最大信息系数加权来反映关联特征, 最后使用某工业园区的实际监测数据中的CO浓度与其他污染气体浓度进行动态关联分析实验. 结果表明, 该方法可以有效提取数据的动态关联特性, 能够很好地反应出CO浓度异常的其他影响因子和时间信息, 为工业园区废气污染溯源提供了重要的参考信息. 文中选用的CO气体类型是示例, 也可以用于其他气体以及其他影响因素的计算. 未来可以分析多站点之间动态关联度, 在空间维度上将多个站点联系起来, 提取数据的时空特征, 推理污染路线.2.3 动态关联分析算法
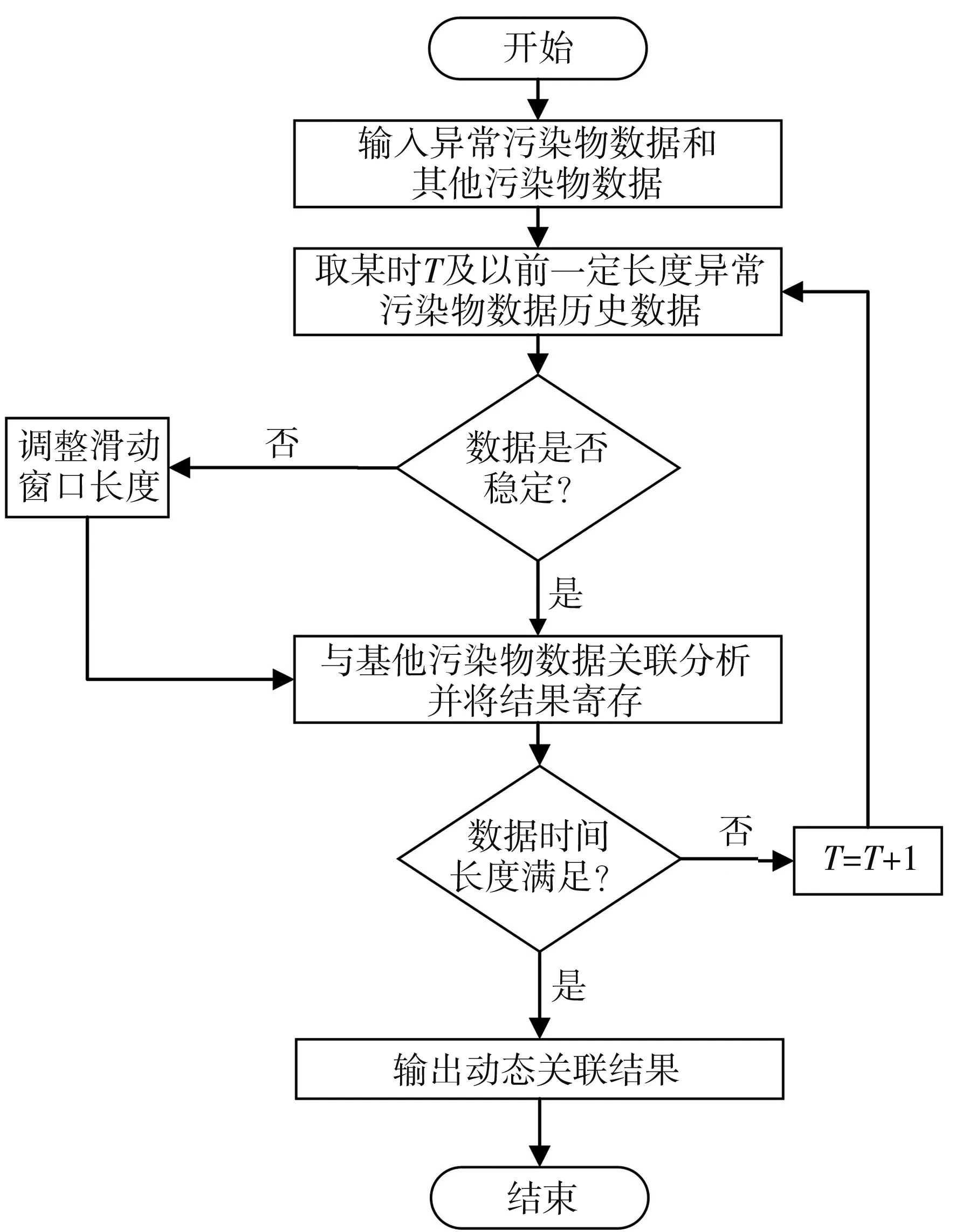
3 实验及结果
3.1 实验数据及实验设置
3.2 实验1

3.3 实验2

3.4 实验3



4 结束语

