考虑死区与延时影响的LCL型并网逆变器谐波特性分析
班国邦,曾华荣,张露松,朱雯清,李建文
(1.贵州电网有限公司 电力科学研究院,贵州 贵阳 550002;2.防冰减灾重点实验室(南方电网公司),贵州 贵阳 550002;3.华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引言
逆变器作为新能源发电和电网之间的能量转换和传输接口,多用于风电光伏并网、城际动车组并网系统中。多样化的电力电子设备与电网间存在强耦合。大规模新能源接入电网易引起宽频带振荡等问题[1-3]。谐波超标会影响电力设备的安全运行,严重时会导致系统失稳;因此展开并网逆变器的谐波特性分析是推进“双高”电力系统发展的基础[4-6]。
脉冲宽度调制技术(pulse width modulation,PWM)在并网逆变器中应用广泛,但其应用会产生载波频率及整数倍载波频率及其附近的谐波[7]。在逆变器的运行中,为防止桥臂出现直通现象,需在开关器件的控制信号中加入一定的延时;但死区效应会引入死区电压,使输出波形出现畸变,使含有的低次谐波成分进一步影响并网逆变器的电流质量[8-10]。
针对PWM引起的高次谐波,通常在逆变器和电网之间加入滤波环节。LCL型滤波器体积小、成本低,因而得到了广泛应用;但其频率响应存在谐振尖峰,若不对谐振尖峰加以有效阻尼会威胁系统的稳定运行[11]。通常,并网系统控制侧采用离散采样,PWM调制信号会引入数字延时。实际系统中,通过改变延时影响虚拟阻尼的抑制作用[12-15]。
本文首先从理论角度分析逆变器输出 PWM方波电压的谐波特性,进而考虑死区效应分析逆变器输出波形中出现低次谐波分量的机理;然后考虑控制延时对LCL型滤波器固有谐振频率点的影响;最后在仿真平台搭建系统模型,进行相关的仿真验证。
1 典型三相LCL型并网逆变器拓扑
典型三相LCL型并网逆变器拓扑如图1所示。

图1 三相LCL型并网逆变器拓扑Fig.1 Circuit topology of three phase LCL gird-connected inverter
图 1中,ud为直流母线电压;id为直流侧电流;Ta、Tb、Tc为逆变电路三相电路上桥臂;Ta′、Tb′、Tc′为逆变电路三相电路下桥臂;L1、L2、C分别为LCL型滤波器逆变器侧电感、网侧电感及滤波电容;Lg为电网等效电感;iL1、iL2、iC分别为逆变器侧电感电流、网侧电感电流及滤波电容电流;uinv为逆变器输出电压;uC为滤波电容电压;uPCC为逆变电路并网点电压;ug为电网电压。
2 逆变器谐波特性分析
2.1 PWM调制引起的谐波分析
图2给出了某一时刻下,在一个完整的开关周期内,载波与调制波控制功率管开通与关断的过程。
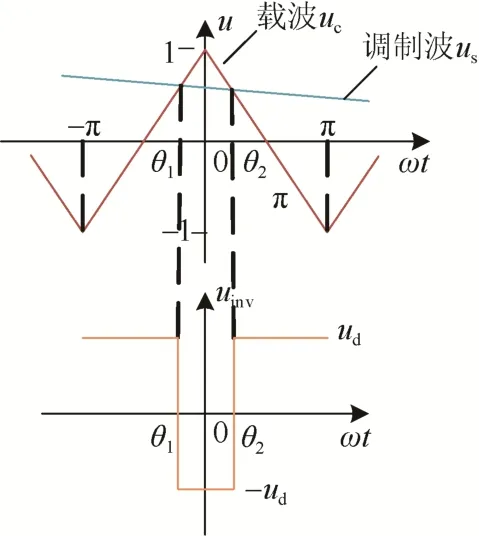
图2 功率管开通与关断的过程示意图Fig.2 Schematic diagram of the process of turning on and turning off the power tube
观察图2,将逆变电路输出电压uinv表示为:

式中:ωc为载波频率;θ1为导通角;θ2为关断角。将逆变电路输出电压uinv与直流母线电压ud做比,并用傅里叶级数展开得到:

式中:第一项为PWM输出波形中基波分量;第二项为谐波部分;a为调制度,其大小为调制波幅值与载波幅值之比,0≤a≤1;ωτ为基波频率。
逆变器通常采用远大于电网频率的开关频率。通过分析 PWM 逆变电路的数学模型,易得逆变器输出的谐波分量主要集中在载波频率ωc、2ωc、3ωc等高次谐波及其附近处。
2.2 逆变器死区效应分析
理想情况下,逆变器同一桥臂上、下功率管开通和关断状态互补;但由于开关器件的非理想特性,器件的开关信号与理想信号间有一定的时间差,且 IGBT的关断时间通常大于开通时间,如图3所示。

图3 IGBT开关过程示意图Fig.3 Schematic diagram of IGBT switching process
图 3中,ugem、icm分别表示栅极电压幅值与集电极电流幅值,Ton和Toff分别表示IGBT开通与关断过程时间。
为防止同一桥臂上、下开关管出现直通现象,通常在其控制信号中加入死区时间,使其提前关断或延时开通,如图4所示。

图4 添加死区时间前后开关信号波形Fig.4 Switch signal waveform before and after adding dead time
图4中,Ba1表示a相上桥臂;Ba2表示a相下桥臂;Td为死区时间。
设置死区时间会引入死区电压,进而影响输出电压波形造成波形畸变。死区时间造成的影响称为死区效应。
死区时间内,同一桥臂上、下功率管均处于关断状态,通过二极管续流。实际工况中,开关器件的开通和关断的驱动信号存在延时,令其分别为To′n和To′ff,则误差时间Tdm为:

式中:ia为a相电流;sgn为符号函数。a相的死区效应产生的误差电压幅值udm为:
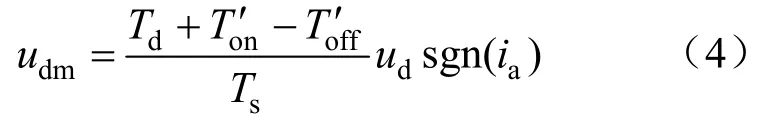
式中:Ts为一个开关周期时间。
将三相误差电压转换至αβ坐标系下,得到:

式中:ud,α、ud,β分别为死区效应在α轴和β轴引起的电压;ia、ib、ic分别为A相、B相、C相电流。进一步将αβ坐标系下的两相电压转换至dq坐标系下,并对符号函数sgn(i)进行傅里叶分解,得到:
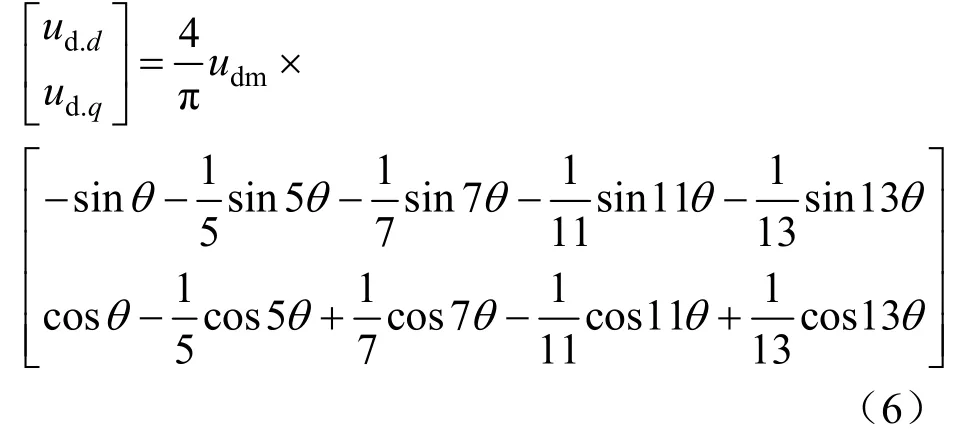
式中:ud.d、ud.q分别为死区效应在d轴和q轴引起的电压;θ表示α轴和A相的夹角。误差电压包括基波和奇次谐波,其主要受5次和7次谐波影响,并且低次谐波含量随死区时间的增加而增加。本文假设三相对称,故输出线电压中没有3次谐波及3的整数倍谐波分量。
2.3 LCL滤波器及控制延时的影响
LCL型逆变器存在固有谐振尖峰。抑制谐振尖峰的方法主要有无源阻尼和有源阻尼2种[11]。无源阻尼方法通过在滤波器支路串联(或并联)电阻来抑制谐振峰。有源阻尼方法通过在控制侧加入虚拟电阻以抑制谐振峰[11],其控制框图如图5所示。图5中,kc为有源阻尼系数。

图5 加入有源阻尼后的控制框图Fig.5 Control block diagram after adding active damping
化简图5,得到逆变器输出电压uinv到网侧电感电流iL2的传递函数:
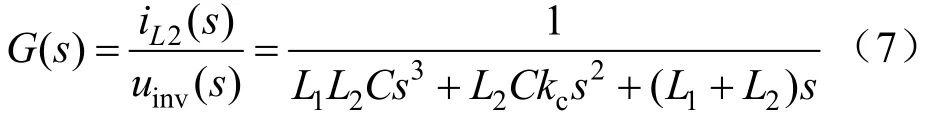
并网逆变器的完整控制框图如图6所示。

图6 未考虑延时影响的并网逆变器控制框图Fig.6 Control block diagram of grid-connected inverter without considering the effect of time delay
图 6中,iref为电流参考值;H(s)为网侧电感电流采样系数;Gi(s)为外环并网电流比例积分控制器,其表达式为;kPWM为逆变器的放大系数,通常取1。
由于在滤波电容两端并联电阻不影响系统低频段与高频段的幅频特性[16],故对上述这一加入有源阻尼的控制框图作等效变换,将其等效为一并联在滤波电容两端的虚拟电阻R,如图7所示。

图7 并网逆变器控制侧等效滤波电容并联虚拟电阻示意图Fig.7 Schematic diagram of the equivalent parallel virtual resistance of the filter capacitor on the control side of the grid-connected inverter
推导得到虚拟电阻R的表达式为:

考虑数字控制调制过程会引入计算延时和调制延时,故在控制回路加入延时环节。加入延时后的系统控制框图如图8所示。
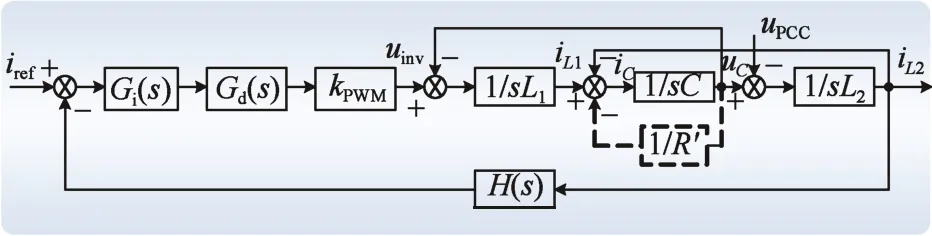
图8 考虑延时影响的并网逆变器控制框图Fig.8 Control block diagram of grid-connected inverter considering the effect of time delay
图8中,Gd(s)为延时等效传递函数,其表达式为Gd(s) = e-1.5sTs。对考虑延时影响的系统控制框图作等效变换,推导得到虚拟电阻R′的表达式为:

根据图6和图8所示的逆变器并网系统控制框图,绘制未考虑延时与考虑延时下系统的传递函数Bode图,如图9所示。
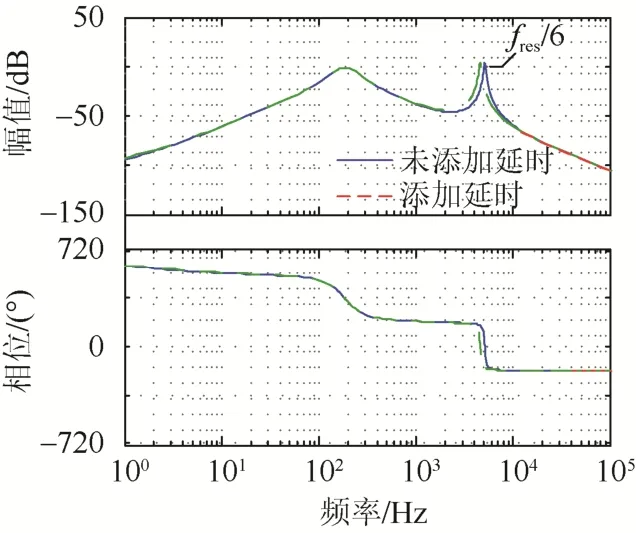
图9 添加延时前后系统谐振频率的偏移Fig.9 Shift of system resonance frequency before and after adding delay

3 仿真验证
根据图1所示的三相LCL型并网逆变器电路拓扑,在 MATLAB/SIMULINK平台搭建仿真模型,参数设置见表1。
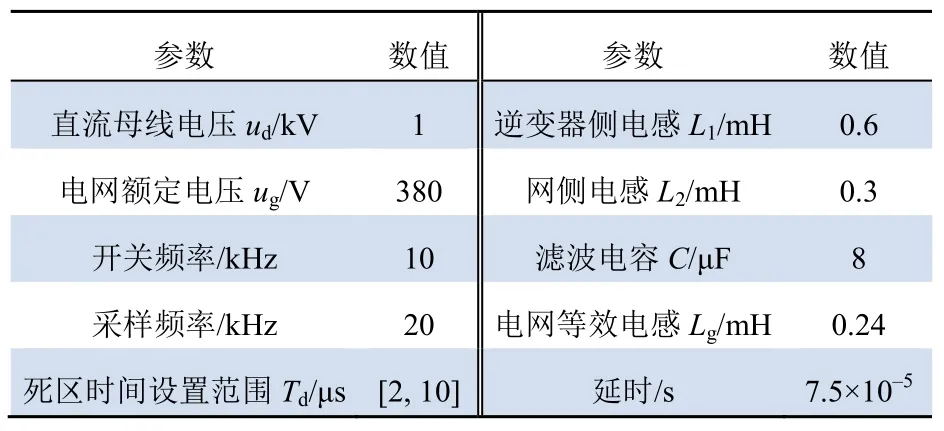
表1 并网逆变器参数设置Tab.1 Parameter setting of the grid-connected inverter
3.1 PWM调制谐波特性分析
基于 PWM 控制的三相全桥逆变器输出电压uinv波形在进行傅里叶分解后,结果如图10所示。

图10 未添加延时情况下逆变器输出电压uinv傅里叶分解结果Fig.10 Fourier decomposition result of the inverter output voltage uinv with no delay added
图10中,逆变器输出电压uinv谐波总含量为116.46%。除去基波外,结果中还含有200次、400次及600次谐波,均在载波频率附近,近似关于载波频率对称;低次谐波含量较少,其中5次谐波含量为0.83%,7次谐波含量为0.41%。
3.2 死区时间影响分析
依次添加死区时间 2 μs、4 μs、6 μs、8 μs及10 μs。死区时间为2 μs时逆变器输出电压uinv波形如图11所示。

图11 死区时间为2 μs时逆变器输出电压uinv傅里叶分解结果Fig.11 Fourier decomposition result of the inverter output voltage uinv when the dead time is 2 μs
观察图11发现,加入死区时间后,逆变器输出电压uinv中低次谐波含量增加,但不含3次及3的整数倍次谐波。
随着死区时间增加,低次谐波含量增大,基波幅值减小,总谐波畸变率增大。利用傅里叶分解不同死区时间下逆变器输出电压uinv的各次谐波含量,结果见表2(其中un表示n次谐波)。
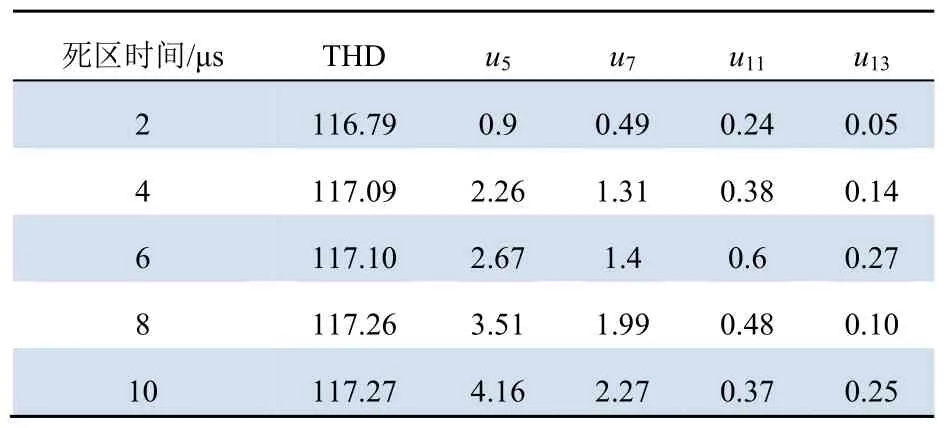
表2 傅里叶分解不同死区时间下逆变器输出电压uinv的总畸变率及各次谐波含量结果Tab.2 Fourier decomposition results of the total distortion rate and the content of each harmonic of the inverter output voltage uinv under different dead time %
由表2可知,5次、7次谐波随死区时间增加而增加,11次和13次谐波没有明显变化。死区时间为2 μs时,5次谐波含量为0.9%,大于无死区时5次谐波的含量0.83%;7次谐波含量为0.49%,大于无死区时7次谐波的含量0.41%。以上结果证明,在功率器件中加入死区时间直接影响低次谐波含量,从而验证了2.2节中死区效应影响谐波含量的结论。
3.3 延时对谐振频率的影响分析
LCL滤波器的固有谐振点会使输出波形含一定谐振频率附近的谐波分量。强电网工况下,电网等效电感Lg近似为0,逆变器固有谐振频率为3.98 kHz(79 p.u.)。仿真中,对逆变器网侧电感电流iL2利用傅里叶级数展开,发现在79次和 83次谐波处存在较丰富的谐波分量,如图12所示。

图12 强电网工况下未加延时情况下逆变器谐振频率附近的谐波Fig.12 Harmonics near the resonance frequency of the inverter with no delay added under strong grid
添加1.5Ts延时后,由仿真结果可得,79次谐波含量为0.13%,83次谐波含量为0.12%。谐波含量变化较小,即延时对强电网谐波谐振影响较小。
弱电网工况下,电网等效电感Lg=0.24 mH,谐振频率为3.34 kHz(66 p.u.)。仿真结果显示,在60次谐波处附近出现明显的谐振频率带,59次和 61次谐波含量较丰富,其值分别为 0.26%和0.25%,如图13所示。
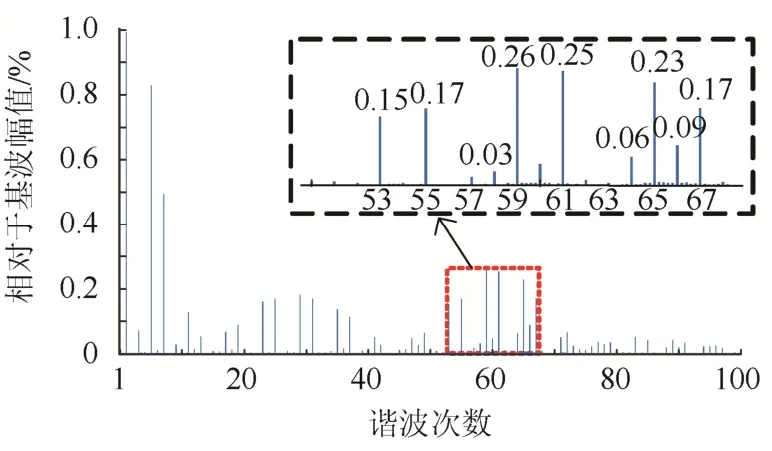
图13 弱电网工况下未加延时情况下逆变器谐振频率附近的谐波Fig.13 Harmonics near the resonance frequency of the inverter with no delay added under a weak grid
添加1.5Ts延时后,由仿真结果可得,谐振峰偏移至65次谐波附近,这与谐振频率理论值相符;同时,各谐振频率附近的谐波含量增加明显。59次谐波含量由0.26%增加到0.3%,61次谐波含量由0.25%增加到0.36%,65次谐波含量由0.09%增加到0.46%。具体仿真结果如图14所示。

图14 弱电网工况下添加1.5Ts延时后逆变器谐振频率附近的谐波Fig.14 Harmonics near the resonance frequency of the inverter after adding a 1.5Ts delay under a weak grid
弱电网且未添加延时情况下,谐振频率附近的谐波含量见表3。

表3 弱电网工况下未添加延时情况下谐振频率附近的谐波含量Tab.3 Harmonic content near the resonance frequency with no delay under a weak grid
弱电网下,添加1.5Ts延时后,谐振频率附近的谐波含量见表4。

表4 弱电网工况下添加1.5Ts延时后谐振频率附近的谐波含量Tab.4 Harmonic content near resonance frequency with 1.5Ts delay added under a weak grid
表3与表4深色表示数据分别为未加延时与添加延时后的谐振频率数据。添加1.5Ts延时后,改变虚拟阻尼的大小,谐振频率处的谐波含量有所增加。
由仿真结果可得,在LCL滤波器固有谐振频率处会出现谐振频率带。实际系统中,可通过改变延时来改变虚拟阻尼的抑制能力。强电网中,延时对谐振影响较小;弱电网中,延时对谐振影响较大。谐振频率附近的谐波含量有明显增大,并且谐振峰偏移至理论计算的谐振频率附近。虚拟阻尼能更准确地抑制谐振频率附近的谐波,增强系统的鲁棒性。
4 结论
本文基于三相LCL型并网逆变器,在仿真平台搭建系统模型,实现了逆变器谐波特性的复现,结果表明:
(1)PWM调制技术产生载波频率及其整数倍附近的高次谐波。
(2)考虑功率器件的死区效应后,逆变器输出波形的低次谐波增加,主要为 5次、7次、11次、13次等。随着死区时间增加,总谐波含量增加,5次和7次谐波含量增加明显。
(3)弱电网工况,逆变器固有谐振频率处出现谐振频率带。控制延时间接改变虚拟阻尼值,改变LCL逆变器的谐振频率,适当的添加延时,可使谐振峰处于理论计算的谐振频率处。

