偏心荷载对盘扣式支撑架动力性能的影响

张德波， 张宗富

(1.海南建设安装工程有限公司， 海口 570100； 2.海南建设工程股份有限公司， 海口 570100)

0 引 言

模板支撑架是重大伤亡事故的多发领域，坍塌引发的事故频繁发生。何芳东等[1]研究了2011～2016年，模板支撑架事故数据和资料，总结了坍塌事故发生的基本规律。宋世军等[2]统计分析了高支模工程事故原因，提出了一种高支模工程远程坍塌监测算法。张学智[3]指出高支模整体动力特征认识不足是导致高支撑体系倒塌的重要原因。马利[4]分析了阶跃荷载作用下模板支撑架体系的动力稳定性，发现模板支撑架结构动力稳定性临界荷载值小于静力稳定临界荷载值。

支撑架在实际施工过程中荷载变化较大，浇筑前模板支架上大量材料不均匀堆放、预制构件的局部布置等使支撑架受荷载分布不均匀，对架体带来偏心、侧力、扭转、冲砸等荷载作用，然而支撑架的计算往往忽视或简化了偏心荷载和动力作用[5-6]。陆征然[7-8]提出了考虑偏心荷载作用下的满堂脚手架数值计算模型，参数化分析了偏心荷载对不同脚手架搭设参数承载性能的影响规律，研究了混凝土不同浇筑阶段与浇筑路径对支撑架自振频率的影响，发现混凝土浇筑过程中支撑架受到偏心荷载作用，自振频率逐渐减小。为研究偏心荷载对支撑架动力性能的影响规律，笔者以盘扣式支撑架为研究对象，动力测试支撑架纵向和横向不同荷载布置工况下支撑架自振频率的变化规律，建立支撑架有限元模型，分析不同荷载布置下支撑架的模态，对比计算得到频率与实验测试结果，研究偏心荷载作用下支撑架的振型变化规律，采用响应面法拟合偏心荷载作用时频率与偏载尺寸的变化响应面模型，为支撑架堆载方式与施工顺序优化提供计算依据。

1 实 验

1.1 实验模型

实验模型依据《建筑施工承插型盘扣式钢管支架安全技术规程》JGJ231—2010[9]要求进行设计，实际搭设图和结构设计图分别见图1和2。支撑架使用周转次数均超过7次的构件搭设，立杆钢管外径为48.3 mm，壁厚3.2 mm，水平杆外径48.3 mm，壁厚2.5 mm；主楞和次楞采用截面尺寸为85 mm×35 mm方木。采用动态信号采集仪和2个加速度传感器同时记录支撑架纵向和横向的加速度信号，加速度传感器布置示意见图2。

图1 盘扣式支撑架实验模型搭设Fig. 1 Erection of experimental model of disk lock steel tubular scaffold

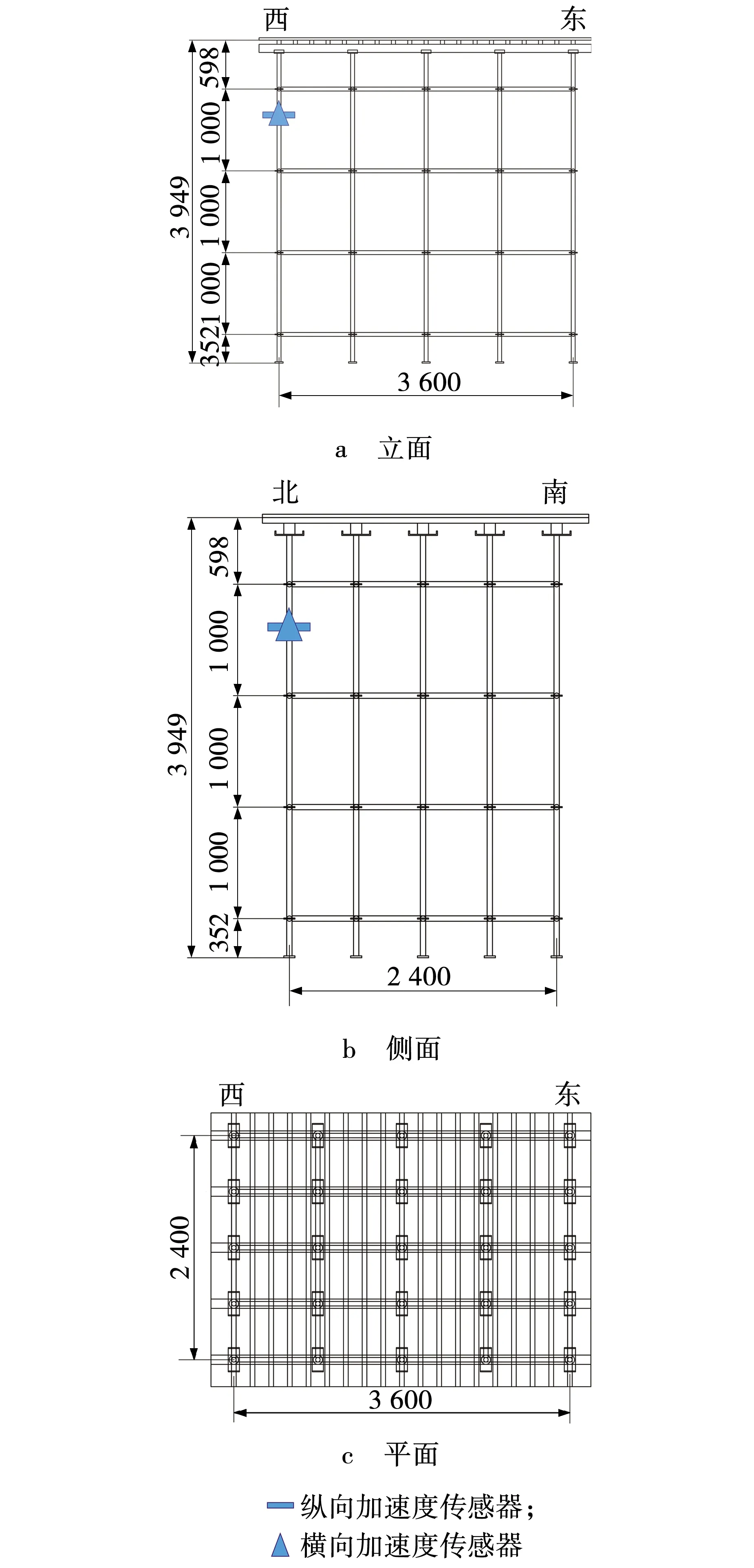
图2 盘扣式支撑架实验设计模型Fig. 2 Experimental design model of disk lock steel tubular scaffold

1.2 加载方法

将模板平面用木方条分隔成若干区域，实验过程中根据工况要求将砂袋均匀堆放至指定区域内，每次加载的砂袋总质量均为500 kg，每次堆放后静置10 min，接着用长绳侧向拉动支撑架上部立杆，使支撑架发生纵向和横向振动，停止拉动后记录加速度信号。

1.3 测试结果与分析

各工况、砂袋堆放区域，以及支撑架前5阶测试结果见表1，表中，fm1、fm2、fm3、fm4、fm5分别表示支撑架前5阶频率实测值。其中，砂袋堆放区域A1～A9，如图3所示。为研究偏心荷载(简称偏载)对支撑架动力性能影响，表1中G9工况给出满布荷载时的频率值，以便与其他偏载情况进行对比。G1～G4工况是偏载尺寸沿纵向变化，G5～G8工况是偏载尺寸沿横向变化。另外，表1中，G2工况与G6工况砂袋的堆放面积相同，G2是纵向尺寸变化过程，G6是横向尺寸变化过程，两者分别进行了动力测试。分别计算G1～G4、G5～G8加载工况各阶频率值与满布荷载G9工况频率值的差值(Δf1、Δf2)，绘制频率差值图见图4。

图3 盘扣式支撑架实验砂袋堆放区域示意Fig. 3 Schematic of stacking area of experimental sand bags of turnbuckle support frame

从表1和图4可知，偏载作用下，第1阶频率值均小于G9工况对应的频率值，最小值较G9工况频率值减小8.89%；第2阶频率值均小于G9工况对应的频率值，最小值较G9工况频率值减小7.18%；第3阶频率值均大于G9工况对应的频率值，最大值较G9工况频率值增加22.79%；第4阶频率值在G9工况第4阶频率值附近出现一定波动，变化值为G9工况频率值的-1.07%～0.51%之间；第5阶频率值在G9工况第5阶频率值附近波动，变化值为G9工况频率值的-3.04%～1.65%之间。可见偏载的存在对各阶频率均有一定影响，且对各阶频率的影响各不相同，其中，对第3阶频率值影响最大，其次是第1阶和第2阶频率值，对第4阶和第5阶频率值影响较小。

表1 各工况砂袋堆放区域与各工况前5阶频率实测值

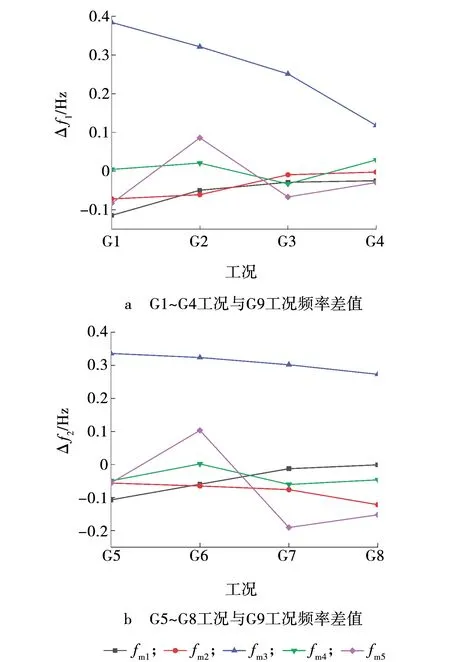
图4 纵向和横向堆载面积变化与满布时频率差值Fig. 4 Difference between change of longitudinal and transverse stacking area and frequency of full distribution

对比图4a和4b可以看出，第1阶频率在偏载分布尺寸分别沿纵向和横向增大时均逐渐增大，并趋近于G9工况第1阶频率值；第2阶频率在偏载分布尺寸分别沿纵向和横向增大时变化规律截然相反，偏载分布尺寸沿纵向增大时第2阶频率值逐渐增大并趋于G9工况第2阶频率值，而沿横向增大时第2阶频率值逐渐减小并远离G9工况第2阶频率值；第3阶频率受偏载分布纵向尺寸影响较大，在偏载分布尺寸分别沿纵向和横向增大时虽然均逐渐减小并趋于G9工况第3阶频率值，但沿纵向频率值变化较大，沿横向频率值变化较小；第4阶频率值在偏载分布尺寸分别沿纵向和横向增大时均在G9工况频率值附近出现较小的波动；第5阶频率值在偏载分布尺寸分别沿纵向和横向增大时均在G9工况频率值附近出现一定波动。说明了偏载分布尺寸对各阶频率有一定影响，且偏载尺寸沿纵向和横向尺寸变化对各阶频率影响规律不相同。

综上所述，偏载对各阶频率均有一定影响，其中，对第3阶频率值影响最大，其次是第1阶和第2阶频率值，对第4阶和第5阶频率值影响较小。此外，偏载分布尺寸沿纵向和横向变化时各阶频率的变化规律各不相同，因此，考虑偏载对支撑架振动频率影响时不仅要考虑偏心荷载的大小，还应考虑偏心荷载的分布尺寸。

2 不同偏载工况的动力性能

2.1 有限元模型的建立

盘扣式支撑架为承插型钢管支架，主要由立杆、水平杆、斜杆、底座和可调顶托组成。支撑架搭设时立杆与立杆之间为承插对接，考虑水平杆和自重作用下，立杆在承插处不发生转动和相对移动，支撑架整体性较好，数值模拟时立杆与立杆为刚性连接，水平杆和立杆采用BEAM188进行模拟。模板结构通过次楞和主楞传递荷载，次楞直接钉在模板底部，主楞直接横跨在可调顶托上，数值模拟时不建立次楞模型，将次楞重量等效到模板上，主楞用BEAM188模拟，模板用SHELL181模拟，主楞与模板单元共享节点，立杆与主楞之间假定为铰接。支撑架节点为半刚性节点，数值模拟时不考虑节点的非线性特性，以线性弹簧单元COMBIN14模拟，节点模拟方法可参考文献[10-11]。另外，支撑架数值模拟时不考虑构件材料的初始缺陷。

采用有限元分析软件ANSYS建立有限元模型，支撑架构件和结构尺寸与实验架体构件和结构尺寸一致，盘扣式支撑架有限元模型见图5。其中，立杆和水平杆的弹性模量均为2.06×105N/mm2，泊松比为0.3，密度为7.85 kg/m3。主楞密度取114.92 kg/m3，泊松比为0.3。模板密度为556.73 kg/m3，泊松比为0.3。节点弹簧刚度的取值8.6×107N·mm/rad[8]。

图5 盘扣式支撑架有限元模型Fig. 5 Finite element model of disk lock steel tubular scaffold

2.2 有限元计算结果与分析

有限元计算时，工况Y1～Y9荷载布置方式分别对应测试实验时的工况G1～G9荷载堆放布置。采用模态分析计算支撑架各个工况下前5阶频率值，见表2，其中：fe1、fe2、fe3、fe4、fe5分别表示支撑架前5阶频率有限元计算值；e1、e2、e3、e4、e5分别表示有限元计算结果fe1、fe2、fe3、fe4、fe5与实测结果fm1、fm2、fm3、fm4、fm5之间的误差值。分别计算Y1～Y4、Y5～Y8加载工况各阶频率与Y9加载工况对应频率的差值绘制频率差值(Δf3、Δf4)如图6所示。

由表2可知，有限元计算结果与实测支撑架频率基本吻合，误差在1.75%～8.27%之间。此外，从表2还可以看出，各工况实测支撑架频率均比有限元计算结果小，这主要是因为支撑架建模时采用的假定与简化方法一定程度上提高了模型的整体刚度，使频率值计算结果偏大。

由表2和图6可知，偏载作用下，第1阶频率值均小于Y9工况对应的频率值，最小值较Y9工况频率值减小10.49%；第2阶频率值均小于Y9工况对应的频率值，最小值较Y9工况频率值减小8.45%；第3阶频率值均大于Y9工况第3阶频率值，最大值较Y9工况频率值增加24.86%；第4阶频率值变化很小，仅为Y9工况值的-0.001 7%～0.240 0%之间；第5阶频率值的变化相对较小，为Y9工况值的-0.001 5%～-1.160 0%之间。由此可见，偏载对第3阶频率值影响最大，其次是第1阶和第2阶频率值，对第4阶和第5阶频率值影响较小，这与实测结果偏载对频率值的影响规律基本一致。

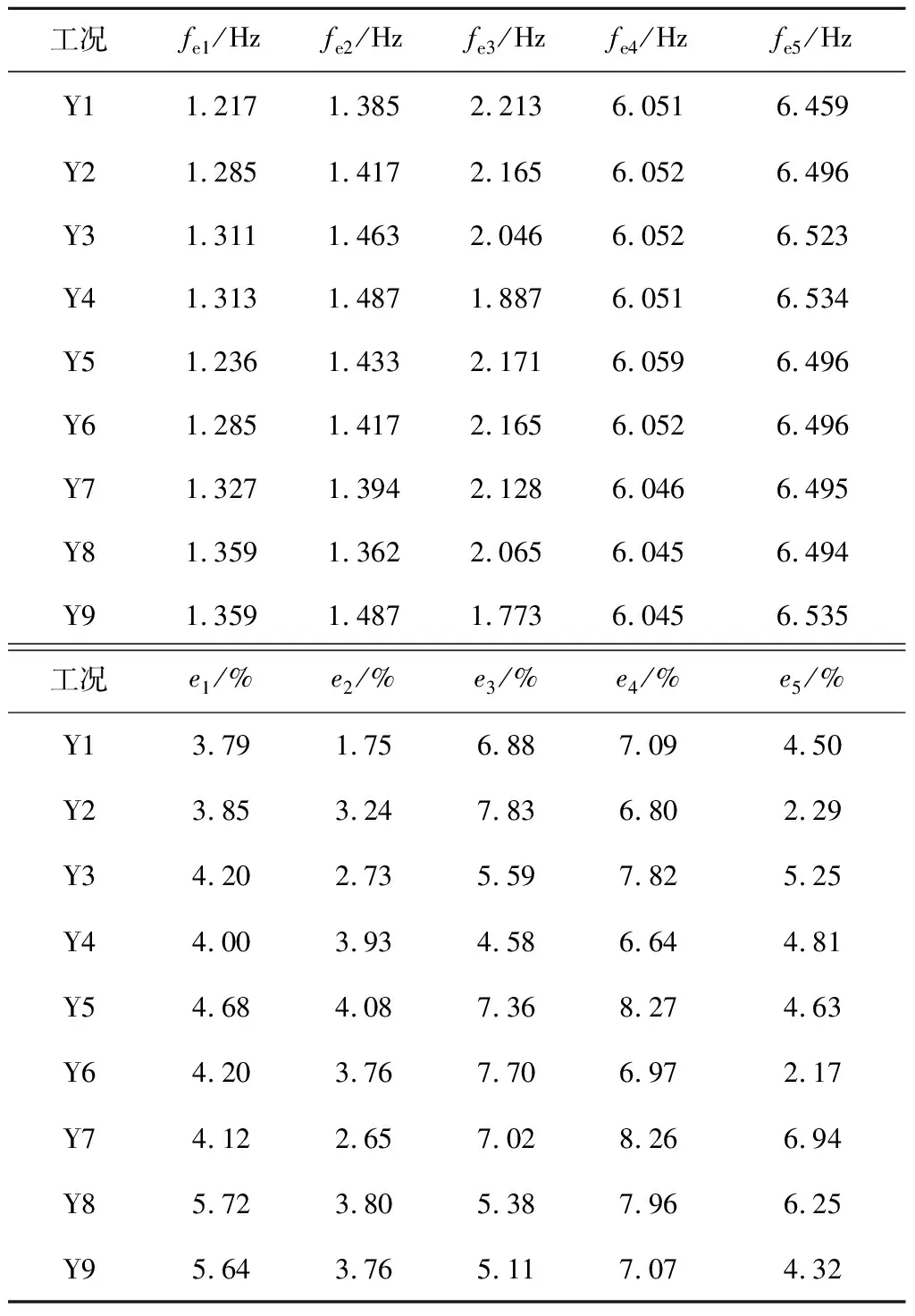
表2 支撑架各工况前5阶频率值计算结果

对比分析图4和6可知，偏载分布尺寸分别沿纵向和横向变化时有限元结果与实测结果前4阶频率的变化规律基本一致。第5阶频率值在偏载分布尺寸沿纵向增大时逐渐增大并趋近于Y9工况频率值，沿横向增大时基本没有变化，未出现波动。这与实测结果中第5阶频率值在G9工况对应频率值附近出现波动规律不太一致，实测结果出现较小的波动主要是由测试误差引起的。

综上所述，有限元计算结果与实测结果基本吻合，偏载分布尺寸沿纵向和横向变化时各阶频率值变化规律基本一致，因此，基本上可证明该有限元模型的准确性。

有限元模态分析得到Y9和Y1加载工况前5阶振型见图7。由图7a可看出，Y9加载工况支撑架第1阶、第2阶振型分别是纵向和横向平动；第3阶振型为扭转；第4阶、第5阶振型分别是纵向和横向立杆弯曲振动。由图7b可看出，Y1加载工况支撑架第1阶、第2阶振型分别是纵向和横向平动，同时伴有扭转；第3阶振型为扭转；第4阶、第5阶振型分别是立杆纵向和横向弯曲振动，同时伴有扭转。对比图7a和图7b可见，支撑架在偏载作用下发生振动时平动和弯曲振型均伴有一定扭转振动。

图6 纵向和横向堆载面积变化与满布时频率差值Fig. 6 Difference between change of longitudinal and transverse stacking area and frequency at full load

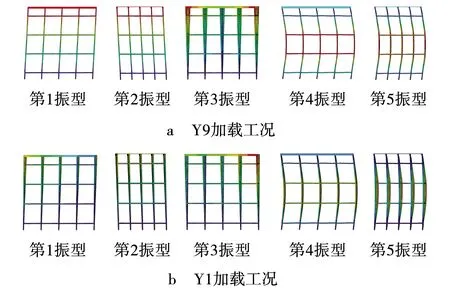
图7 Y9和Y1加载工况前5阶振型Fig. 7 First five modes of Y9 and Y1 loading conditions

3 动力性能的响应面模型

3.1 实验设计

采用响应面法[12-13]拟合支撑架各阶频率与偏载纵向和横向尺寸之间的数值关系。选取堆载面纵向长度L1和横向长度L2为设计参数，见图8。L1和L2的取值范围见表3。考虑偏载对支撑架第4阶、第5阶有限元模型频率计算结果影响不大，仅选取支撑架前3阶频率作为目标输出。利用响应面分析软件Design Expert进行实验设计，实验设计方法运用D-最优设计方法，一共进行20次实验。

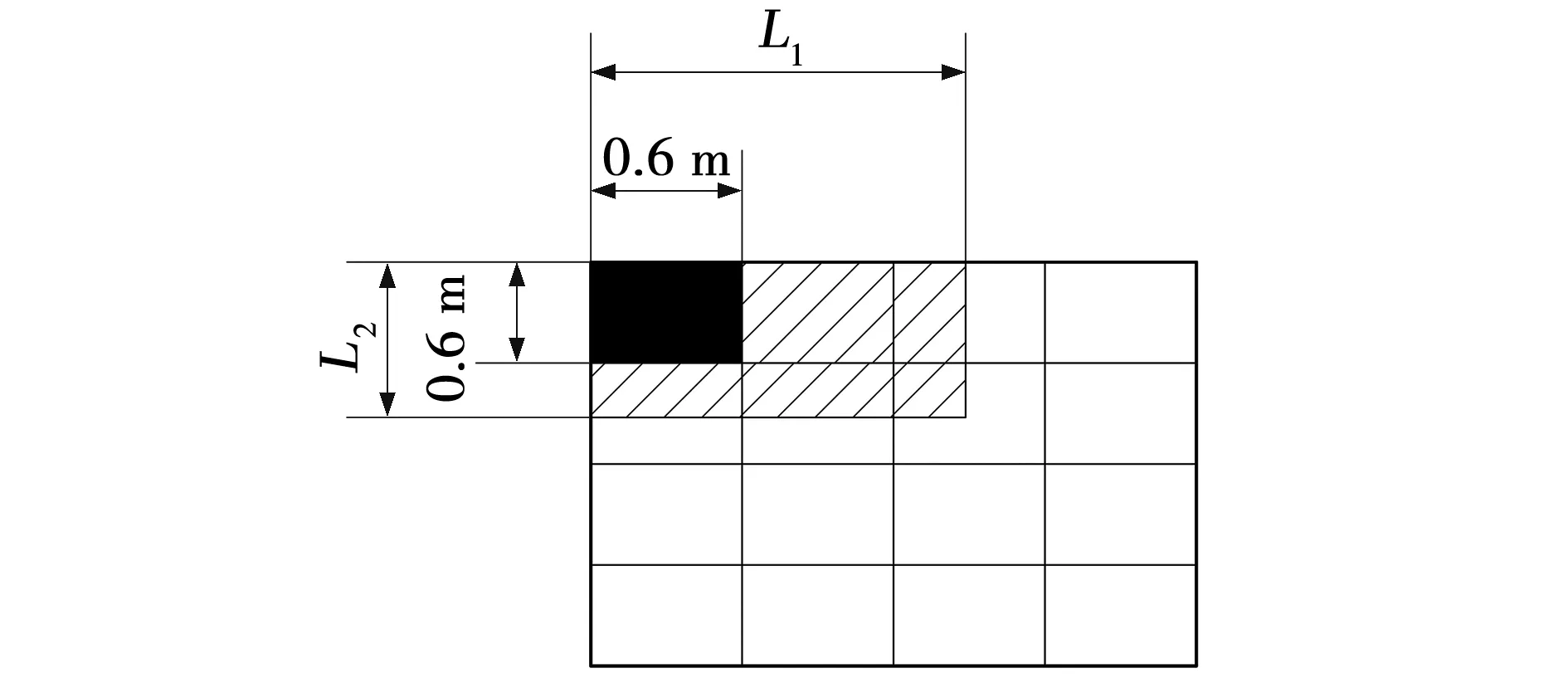
图8 堆载面尺寸变化示意Fig. 8 Schematic of size change of stacking surface

表3 盘扣式支撑架实验参数初始值

3.2 响应面模型拟合及分析

基于P值法[12]选取显著变量，采用三次多项式拟合并得到响应面方程见式(1)～(3)，其中，f1、f2、f3分别表示前3阶频率。采用R2值法[12]对前3阶频率拟合精度进行检验，计算得到R2值见表4。选定三组偏载面积尺寸，分别比较有限元模型和响应面模型计算的频率值，见表5，其中：ft1、ft2、ft3分别表示前3阶频率有限元计算值；fs1、fs2、fs3分别表示前3阶频率响应面计算值；er1、er2、er3分别表示前3阶频率有限元计算值与响应面计算值之间的误差。

(1)

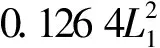
(2)

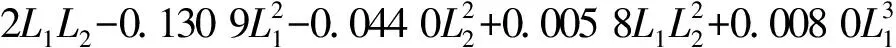
(3)

表4 各阶频率回归判定系数

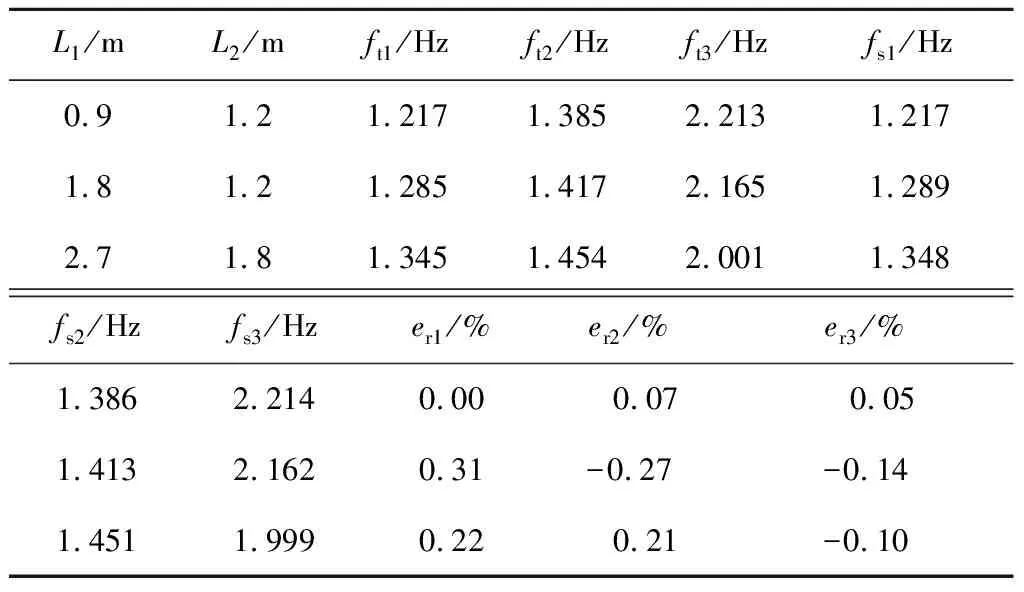
表5 三组偏载尺寸有限元计算及响应面计算结果

由表4可见,前3阶频率响应面模型R2值接近1，说明拟合精度较高。由表5可见,响应面模型式(1)～(3)计算结果与有限元结果误差较小，基本可以替代有限元模型进行计算。实际应用时如装配式叠合板布置顺序、混凝土浇筑顺序时，可根据支撑架的平面尺寸，计算拟合出频率与堆载面尺寸的响应面模型，为支撑架堆载方式和施工顺序优化提供计算依据。

4 结 论

(1)实测结果表明，偏载对支撑架各阶频率均有一定影响。偏载影响下，支撑架第1阶、第2阶和第3阶频率值变化较大，第4阶和第5阶频率值变化较小。此外，偏载分布尺寸沿纵向和横向变化时各阶频率的变化规律各不相同。因此，考虑偏载对支撑架振动频率影响时不仅要考虑偏心荷载的大小，还应考虑偏心荷载的分布尺寸。

(2)偏载对支撑架各阶频率和振型有一定影响，支撑架在偏载作用下发生振动时平动和弯曲振型均伴有一定扭转振动。

(3)支撑架各阶频率与偏载尺寸的响应面模型拟合精度较高，与有限元计算结果之间误差较小，基本可以替代有限元模型进行计算，具有一定的实用价值。