阻尼器特性对力修正迭代混合实验收敛性的影响

王 涛， 浩杰敦， 孟丽岩， 郑 欢， 王 贞， 许国山

(1.黑龙江科技大学 建筑工程学院， 哈尔滨 150022； 2.武汉理工大学 土木与建筑学院， 武汉 430070； 3.哈尔滨工业大学 土木工程学院， 哈尔滨 150090)

0 引 言

Nakashima等[1]于1992年提出的实时混合实验，将结构非线性强、关键复杂部位分离出来作为试验子结构(Experimental substructure，ES)进行加载，其余部位作为数值子结构(Numerical substructure，NS)进行模拟实验，构建高速数据交换系统使得两者数据实时传递。由于计算与加载要求同步进行，时滞问题便成了影响实时混合实验精度的主要问题。针对这一问题，国内外学者开展了一系列研究，提出一系列时滞补偿方法[2-4]。郭进等[5-6]于2016年提出了迭代混合实验(Iterative hybrid test，IHT)，该方法将ES与NS分成了两个独立的部分，只在实验开始与结束时进行一次数据交互，避开了时滞问题。由此一些学者对IHT方法开展了一系列研究[7-8]，验证了该方法对于结构的适用性，其中郑欢[9]针对该方法在数值计算时恢复力存在轮次不一致的问题，提出了力修正迭代混合实验方法(Force correction iterative hybrid test，FC-IHT)，并对该方法进行了验证。该方法相较于IHT方法有更好的收敛性。然而，该方法在对恢复力进行修正时将ES等效为线性模型，在实验过程中ES非线性往往较强，于是，对该方法收敛性的影响，尚需要开展进一步研究。

文中首先介绍了FC-IHT方法的原理及流程，将具有黏滞阻尼器的单层框架结构作为研究对象，再以黏滞阻尼器作为ES，其余部位作为NS，分别开展了不同黏滞阻尼器速度指数、阻尼系数下FC-IHT方法的数值模拟；比较了不同工况下速度指数与阻尼系数对于FC-IHT方法的收敛性，探究了黏滞阻尼器速度指数的非线性变化规律以及对于FC-IHT方法的收敛步数、迭代误差、位移时程的影响规律；研究了阻尼大小对于FC-IHT方法的收敛步数、迭代误差的影响规律。

1 实验方法与原理

IHT方法的运动方程为

(1)

式中：MN、KN、CN——NS的质量矩阵、刚度矩阵、阻尼矩阵；

i——计算积分步数。

FC-IHT方法解决了IHT方法ES恢复力在进行运动方程求解时，存在轮次不一致的问题。由式(1)可得，第j轮次的恢复力是由第j-1轮次所得，为使得采集的恢复力更加准确，FC-IHT方法利用相邻两迭代轮次ES位移、速度差值与等效ES数值模型对恢复力进行修正。FC-IHT方法运动方程为

(2)

(3)

式中：γ——等效ES数值模型精度系数；

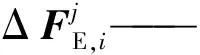
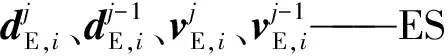
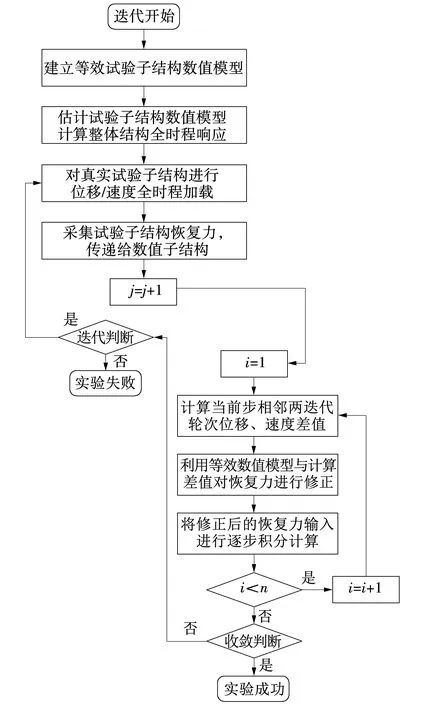
图1 FC-IHT方法原理Fig. 1 Principle of force correction iterative hybrid test

FC-IHT方法的具体流程如下：

(1)前期准备。针对真实的ES开展前期实验，根据实验结果所得到的恢复力、位移、速度计算出等效ES数值模型刚度和阻尼，建立等效ES数值模型。

(2)首轮迭代。设定结构参数，外部激励，初速度与初位移。估计ES数值模型，计算整体结构全时程响应。采集位移、速度响应对真实的ES进行加载，采集加载得到的恢复力，并传递给NS。

(3)恢复力修正。计算出相邻两迭代轮次的位移、速度差值并与等效ES数值模型对恢复力进行修正，并计算出修正后的恢复力。

(4)多轮迭代。将修正后的恢复力参与运动方程求解，进行下一轮结构的逐步积分计算，得到相应的结构响应。

(5)收敛判断。定义评价指标，根据计算所得到的结构响应进行收敛性判断，若收敛则实验成功，若不收敛则进行迭代判断。

(6)迭代判断。由于实验不可能一直进行迭代加载，所以会有一个轮次限定。若当前轮次小于规定值则返回到第(2)步继续迭代，若当前迭代轮次大于规定值，则实验失败。

由原理流程可以得出：ES不同的特性会影响FC-IHT方法等效ES数值模型的刚度和阻尼的计算结果，即会影响式(3)中等效ES数值模型的建立，从而影响式(2)中恢复力的修正，对于不同特性的ES则会有不一样的收敛特性。文中将通过数值模拟进一步讨论黏滞阻尼器非线性程度与阻尼大小对迭代收敛性的影响。

2 数值模拟

2.1 工程概述

为了研究黏滞阻尼器的非线性程度与阻尼大小对于FC-IHT方法的影响规律，开展了整体结构为具有黏滞阻尼器的单层框架FC-IHT数值模拟。该方法将黏滞阻尼器从单层框架结构中分离出来作为ES，其余部位作为NS，通过计算机进行模拟。单层框架黏滞阻尼器FC-IHT的原理如图2所示。在实验开始前会开展前期实验计算出等效ES数值模型的阻尼，建立等效ES数值模型。

在迭代第1轮采用假定的ES数值模型，计算出整体结构全时程响应，采集ES加载命令，对ES进行加载，将加载得到的ES恢复力输入到下一轮次，参与运动方程求解相应的结构响应，同时通过相邻两迭代轮次的速度差值与等效ES数值模型对上一轮次加载得到的ES恢复力进行修正，计算出修正后的恢复力并作为ES本身进行全时程数值计算。通过计算得出作动器全时程的加载命令，再将命令传递给ES进行加载。依次循环，直到实验求解结果收敛，获取相应的结构响应后实验结束。

图2 单层框架力修正迭代混合实验原理Fig. 2 Principle of force correction iterative hybrid test of single layer frame

文中采用的框架质量mN=3.6×105kg，结构刚度KN=1.42×107N/m。结构初始速度与初始位移定义为0，阻尼系数cE=1.81×105(N·s)/m。将一段时长20 s的EL centro(NS，1940)地震波作为输入，积分步长0.01 s，积分步数2 000步。ES为黏滞阻尼器，其力学模型为

FE=cEsgn(vE)|vE|α，

(4)

式中：FE——ES阻尼力向量；

cE——阻尼系数，(N·s)/m；

vE——ES速度向量；

α——黏滞阻尼器速度指数。

逐步积分算法选用翟方法[10]。该方法是一种显式积分方法，可以将位移、速度、加速度进行两步预测。其具体的积分格式为

(5)

式中：aN,i、dN,i+1、vN,i+1——NS计算的加速度向量、位移向量、速度向量；

FE,i——ES加载得到的恢复力向量；

Fi——结构输入的外力向量；

Δt——计算积分步长；

ψ、φ——翟方法引入的参数。

在迭代第一步定义ψ=φ=0，从而使该方法具有积分“自开始”的特性。在后续逐步积分中，定义ψ=φ=0.5。

2.2 评价指标

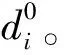
为了定量分析迭代收敛速度，定义迭代收敛步数的评价性指标如式(6)所示，即为该轮次的位移时程与理想状态下该轮次位移时程的位移差值小于规定值G，即认为收敛了δ步。当收敛步数为2 000步时，即认为该工况下迭代完全收敛。该指标能反应在每一轮次下的迭代收敛步数，能够通过图形直观看出收敛的速度。其中规定值G的取值依据实际情况而定，一般设定为小于理想状态下位移幅值的1%。

(6)

为了定量分析迭代收敛精度，定义绝对误差指标如式(7)所示，即每一轮次下位移时程与理想状态位移时程差值的最大值。该指标能够直观的通过图形得出该轮次下局部的误差大小。当局部误差趋近于0时，即认为该工况下迭代收敛。

(7)

2.3 工况设计

为探究黏滞阻尼器非线性程度与阻尼大小对于FC-IHT方法的收敛性，以黏滞阻尼器的速度指数与阻尼系数为研究变量，即通过不同的速度指数与不同的阻尼系数来研究对于FC-IHT的收敛性。速度指数α分别选择0.3、0.4、0.5、0.6、0.7，阻尼系数cE定义放大系数k值即kcE，放大系数k分别选择0.6、0.8、1.0、1.2、1.4。具体模拟工况如表1所示，cEE为等效模型阻尼系数；工况1～5为当放大系数k不变时，不同速度指数α下的FC-IHT模拟；工况6～10为当速度指数α不变时，不同放大系数k下的FC-IHT模拟，并在不同工况下开展前期实验计算出等效ES数值模型阻尼，建立等效ES数值模型。

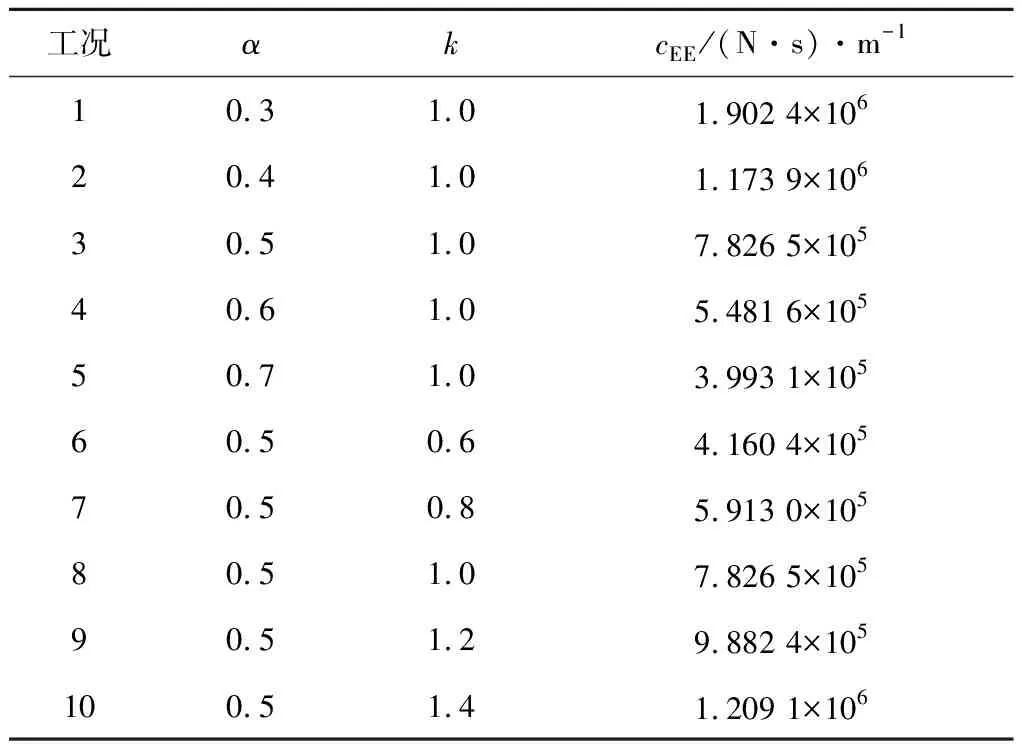
表1 模拟工况

由表1可知，当放大系数k不变，即当黏滞阻尼器的阻尼大小不变时，随着速度指数α的增加，等效ES数值模型阻尼不断减小；当黏滞阻尼器的速度指数α不变，随着放大系数k的增加，即当黏滞阻尼器的阻尼大小变大时，等效ES数值模型阻尼不断增加。

2.4 实验结果分析

工况1～5在不同评价指标下，实验结果如图3～6所示；工况6～10在不同评价指标下，实验结果如图7、8所示。

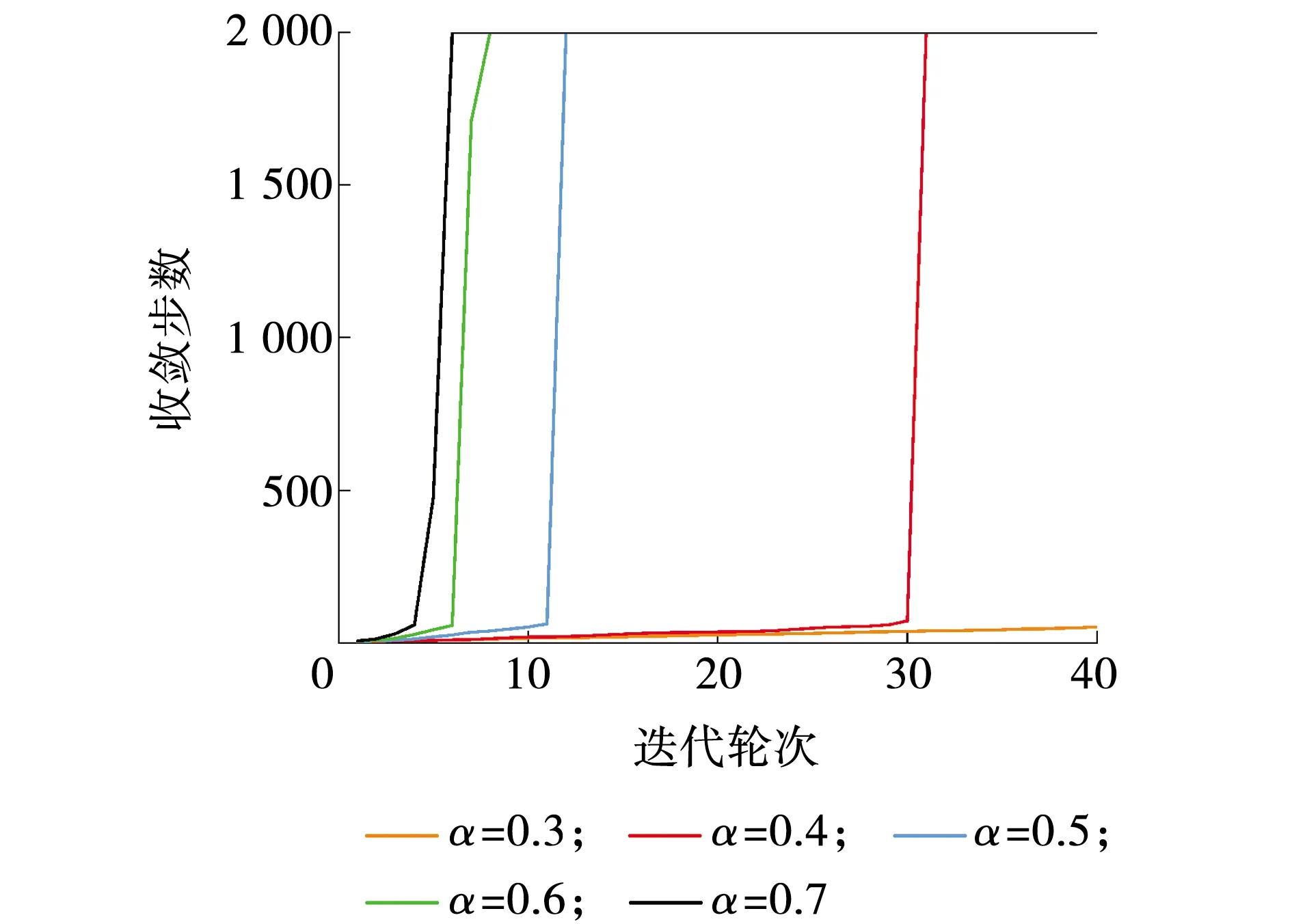
图3 不同速度指数下迭代收敛速度Fig. 3 Iteration convergence speed of different velocity index

不同黏滞阻尼器速度指数下迭代收敛速度如图3所示。由图3可见，在相同迭代轮次下，随着速度指数的增加，迭代收敛步数变多。当速度指数分别取0.4、0.5、0.6、0.7时，迭代完全收敛分别需要31轮、12轮、8轮、6轮，即随着速度指数的增加，迭代完全收敛所需要的轮次变少，迭代收敛速度加快。当速度指数取0.3时，在迭代40轮内不完全收敛。通常开展FC-IHT，迭代轮数不超过20轮。由此可以认为，在该工况下速度指数取0.5～0.7能更好的开展FC-IHT。

不同黏滞阻尼器速度指数下迭代收敛精度如图4所示。当速度指数取0.3时，在前20轮次迭代局部误差e值不趋于收敛；当速度指数分别取0.4、0.5、0.6、0.7时，在相同迭代轮次下，迭代局部误差值逐渐降低，迭代收敛精度提高。不同黏滞阻尼器速度指数下迭代收敛位移s时程响应如图5所示。由图5可见，随着速度指数的增加，在同一时间位移响应的幅值增大，速度变大。

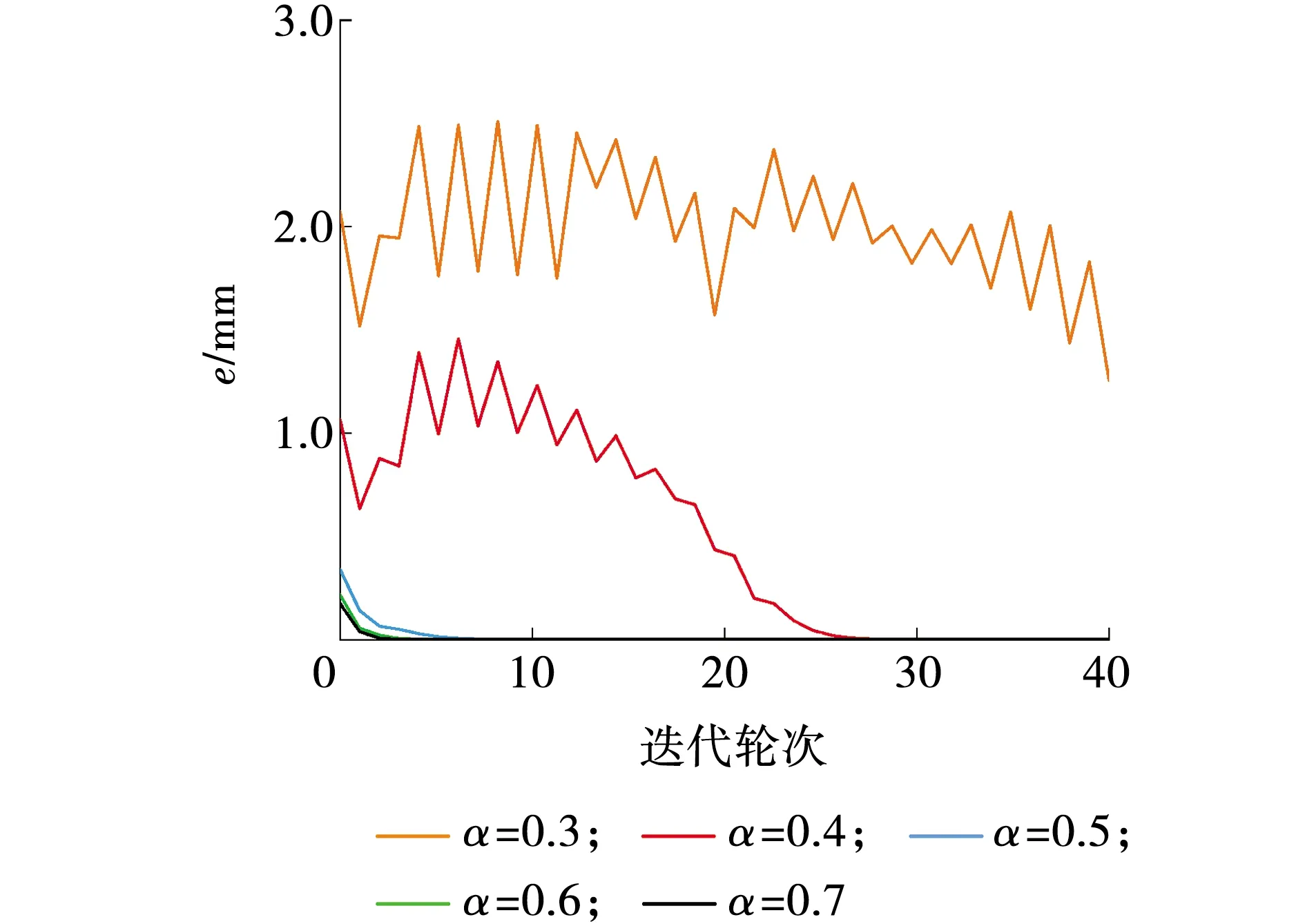
图4 不同速度指数下迭代收敛精度Fig. 4 Iterative convergence accuracy of different velocity index

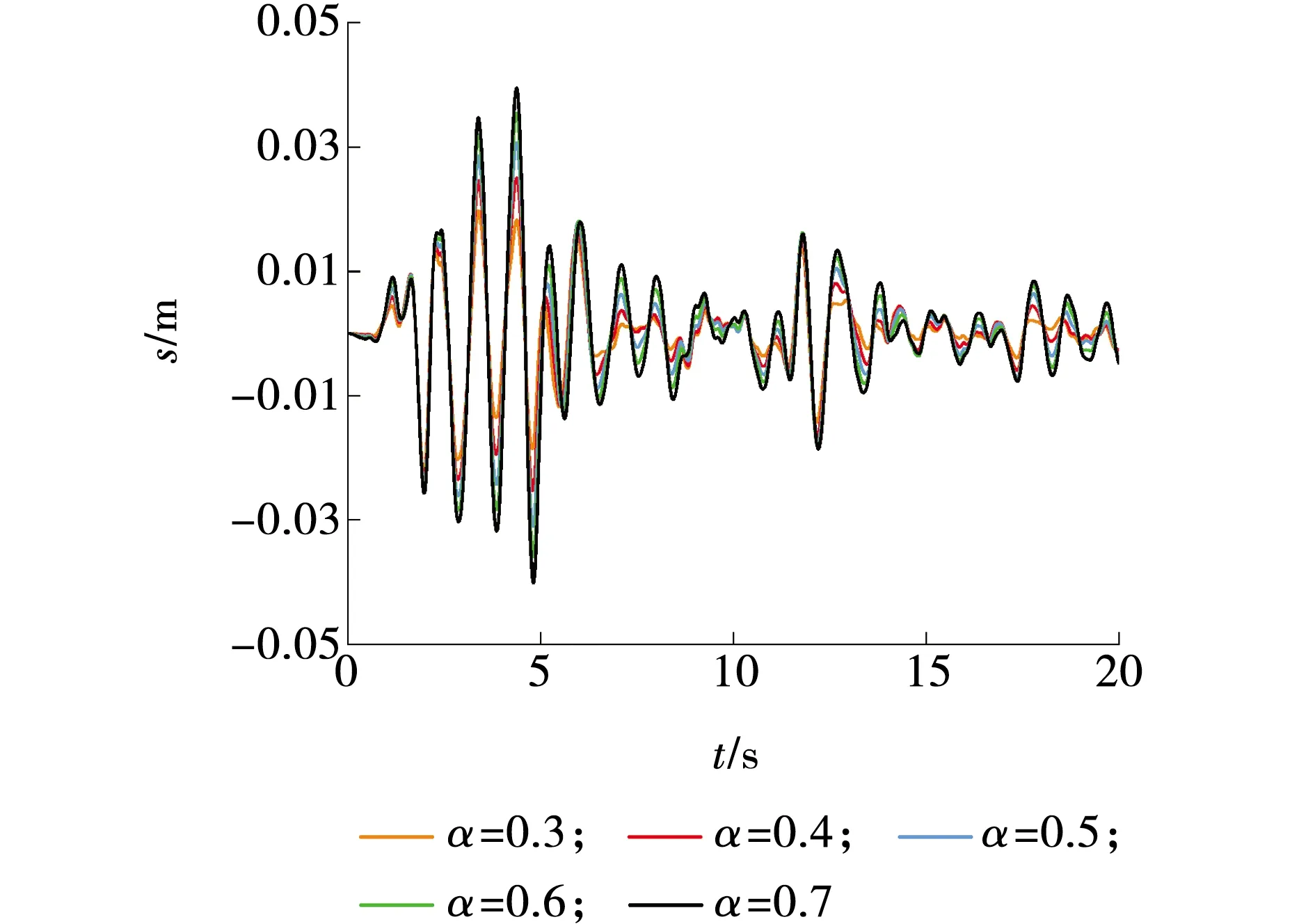
图5 不同速度指数下阻尼器的位移响应Fig. 5 Damper displacement response of different velocity index

不同黏滞阻尼器速度指数下阻尼器阻尼力F与速度曲线如图6所示。当速度指数分别取0.3、0.4、0.5、0.6、0.7时，黏滞阻尼器阻尼力与速度关系处于非线性状态。当速度指数取0.7时，阻尼力与速度曲线趋近于直线，非线性程度比较弱，随着速度指数的减小，阻尼力与速度曲线非线性程度逐渐变强。这表明随着黏滞阻尼器速度指数的增加，黏滞阻尼器非线性程度变弱。

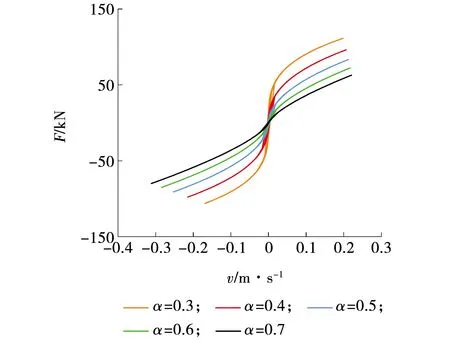
图6 不同速度指数下阻尼器阻尼力与速度曲线Fig. 6 Dampers damping force and velocity curves of different velocity index

不同黏滞阻尼器阻尼系数下迭代收敛速度如图7所示。在相同迭代轮次下，随着k的变大，迭代收敛步数逐渐变少。当k分别取0.6、0.8、1.0、1.2、1.4时，迭代完全收敛分别需要5轮、6轮、8轮、11轮、14轮，即随着k的变大，迭代完全收敛所需要的轮次变多。由此可以认为，在该工况下，FC-IHT方法对于黏滞阻尼器阻尼较小的情况，迭代收敛速度较快。

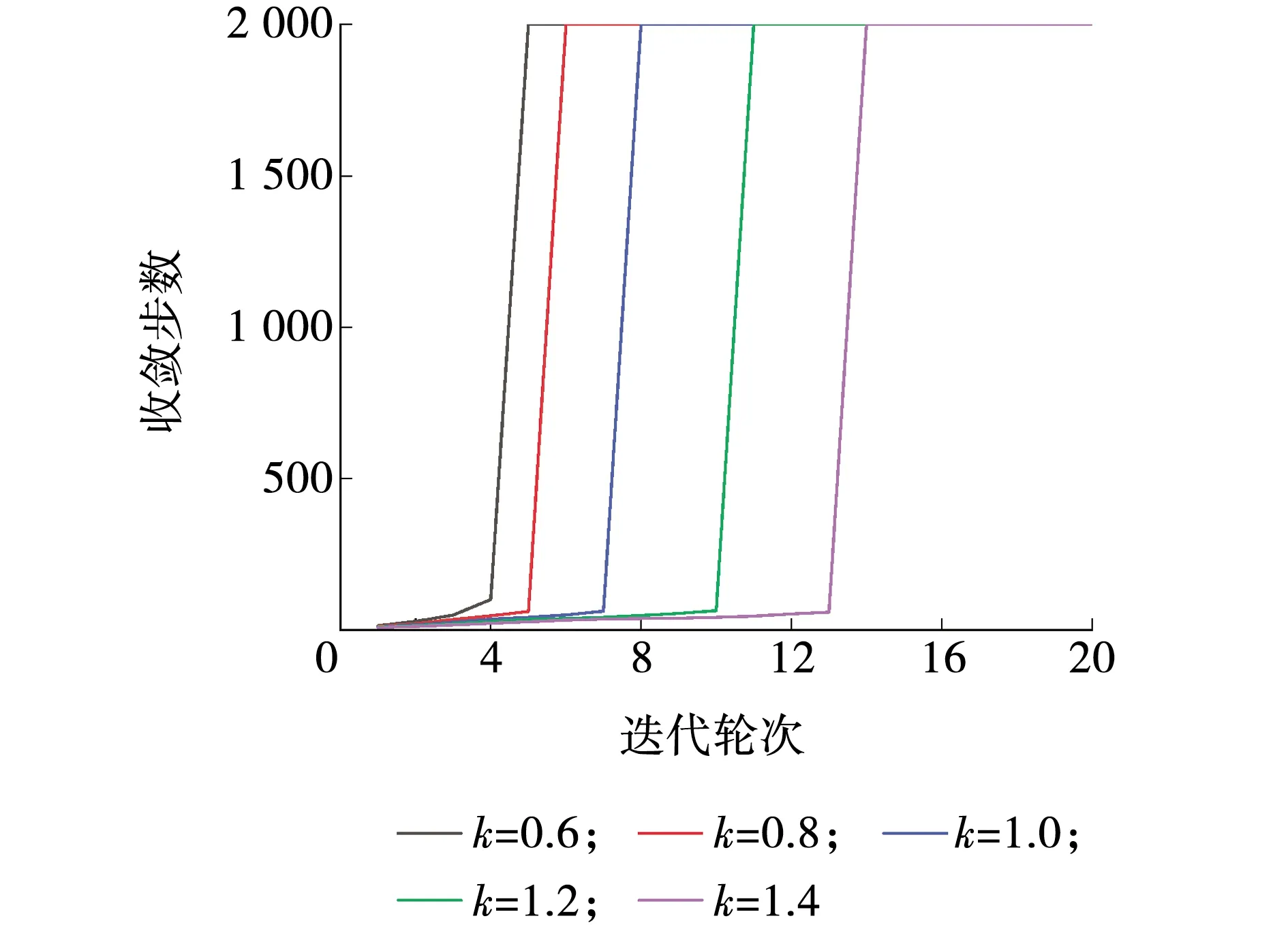
图7 不同阻尼系数下迭代收敛速度Fig. 7 Iterative convergence speed of different damping coefficients

不同黏滞阻尼器阻尼系数下迭代收敛精度如图8所示。随着迭代轮次的增加，当k分别取0.6、0.8、1.0、1.2时，在迭代前两轮，迭代局部误差值迅速降低，迭代两轮后迭代局部误差值逐渐降低；当k取1.4时，在迭代前四轮，迭代局部误差值不稳定，迭代四轮后迭代局部误差值逐渐降低。当k分别取0.6、0.8、1.0、1.2、1.4时，在迭代第一轮，迭代局部误差值与阻尼大小的关系规律不明显，迭代一轮后，在相同迭代轮次下，随着k的增加，迭代局部误差值逐渐增大，迭代收敛精度降低。

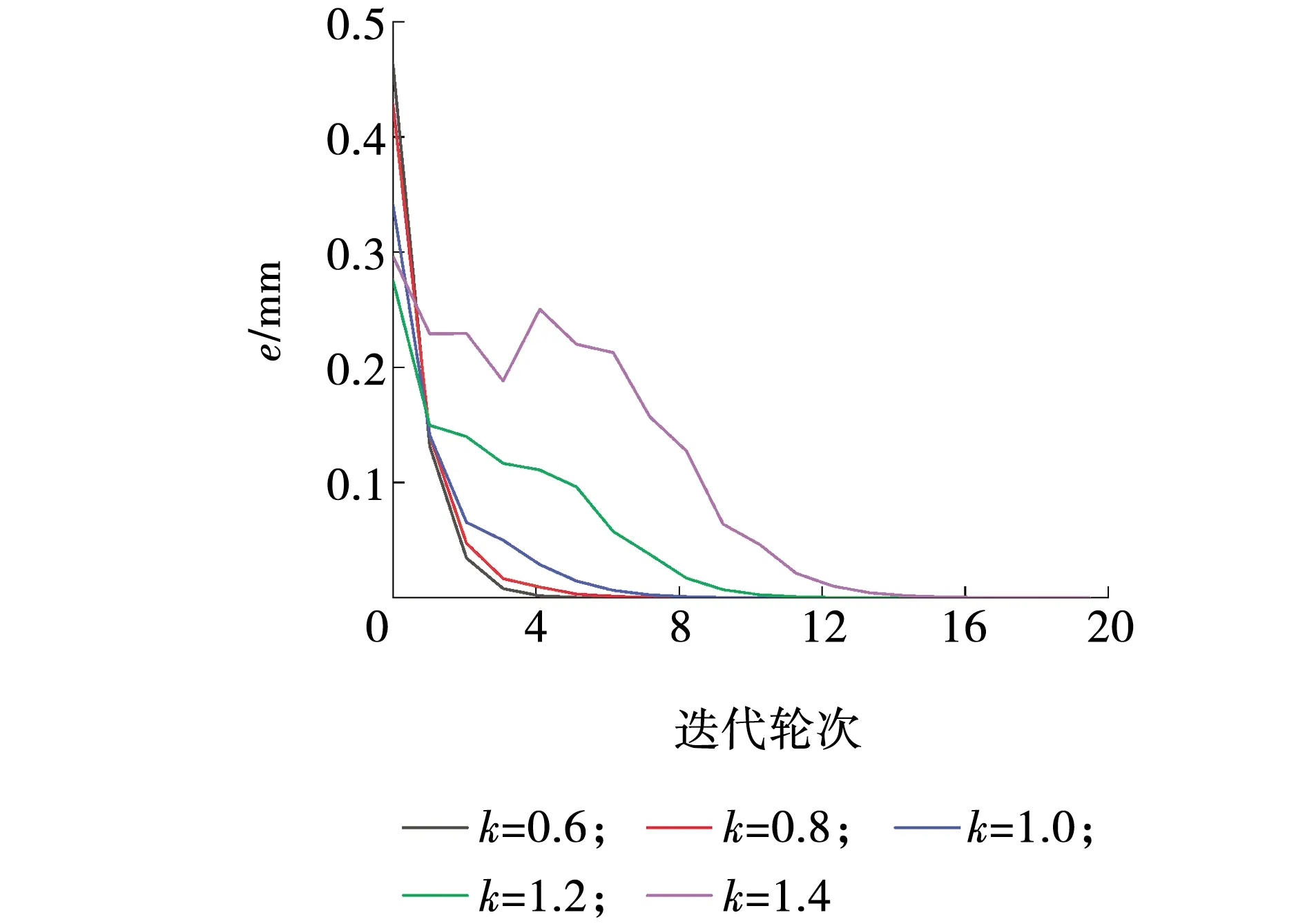
图8 不同阻尼系数的迭代收敛精度Fig. 8 Iteration convergence accuracy of different damping coefficients

3 结 论

(1)黏滞阻尼器非线性越弱，力修正迭代混合实验收敛性越强。根据文中模拟工况，当速度指数分别取0.3、0.4、0.5、0.6、0.7时，阻尼器非线性程度逐渐变弱，迭代完全收敛所需要的轮次逐渐变少，迭代局部误差值逐渐降低，位移幅值逐渐变大，速度逐渐变大。为避免速度过大而导致阻尼器超载，在文中工况下，当速度指数取0.5～0.7时，满足力修正迭代混合实验收敛性要求。

(2)黏滞阻尼器阻尼越大，力修正迭代混合实验收敛性越弱。根据文中模拟工况，当阻尼系数的放大系数k分别取0.6，0.8，1.0，1.2，1.4时，迭代完全收敛所需要的轮次逐渐变多，经过一轮迭代后，迭代局部误差值逐渐增大。在文中工况下，力修正迭代混合实验对于黏滞阻尼器阻尼较小的情况收敛性较强。