考虑倍率的平流层飞艇储能电池建模与分析

刘松松，孙康文

（1.北京航空航天大学 航空科学与工程学院，北京 100083；2.北京航空航天大学云南创新研究院，昆明 650233；3.北京航空航天大学 无人系统研究院，北京 100083）

平流层飞艇因其在科学观测、地面监测和长期通信任务等方面具有良好的应用前景，多年来一直受到国内外技术发达国家的高度重视［1］。为实现平流层飞艇高空长航时的飞行目标，能够获得持续不断的能量无疑是一个至关重要的因素。平流层飞艇所需的能量全部来源于太阳能电池吸收转化的太阳能源，但由于太阳能电池转换效率低且受时空影响输出变化明显、储能电池能量密度低［2］及在飞行器苛刻的质量限制等约束下，平流层飞艇的能量供给能力非常有限，这严重制约了该类飞行器的长航时能力［3-4］。因此，如想实现跨昼夜、甚至长达数月的连续飞行，则必须提高能源系统的容量裕度（存在增重的不利影响），或实现对能源系统的准确监测和有效评估。

储能电池属于能源系统的一部分，随着飞行试验的开展，一些研究者对平流层飞艇的能源系统进行了研究。梁高铭［5］设计了双余度供配电网络，在MATLAB环境中实现了平流层飞艇能源管理系统的全系统仿真。Shan等［6］提出通过调整空速来实现平流层飞艇的能源平衡和区域驻空。Zhang等［7］通过规划飞行姿态，分析了能量平衡问题。以上研究主要集中在平流层飞艇能源系统的总消耗能量与总获取能量的平衡，而没有结合储能电池在飞行条件下的工作特性进行分析。

为表征储能电池的性能，定义以下主要参数，包括：荷电状态（SOC），表示储能电池当前剩余电量占总容量的百分比，是电池剩余供电能力的直观反映；剩余放电时间（RDT），表示按照当前电流放电，储能电池还能持续放电的时间；剩余充电时间（RCT），表示按照当前电流充电，储能电池充满电还需要的时间。对于平流层飞艇，RDT与RCT可直接反映储能电池能否保证飞艇实现跨昼夜飞行所需的航时，对优化能源利用具有指导意义。因此，实时掌握储能电池的SOC、RDT和RCT，可为制定飞行策略、优化能源利用、降低能源系统规模、提高载荷能力提供量化支撑。

在电池的SOC、RDT和RCT量化计算方面，国内外开展了大量的研究。Dai等［8］采用基于等效电路的“平均电池”模型，得到了电池组的平均SOC，再通过“平均单元”与单个单元之间的性能差异，估计所有单元的SOC。Ouyang等［9］提出了一种基于单粒子电化学模型的扩展等效电路模型，提高了低SOC状态下的SOC估算精度。Zhang等［10］进行了不同温度（-20℃、-10℃、0℃、10℃、25℃）和不同电流倍率（0.5C、1C、1.5C）下的测试，并建立了电池动态特性的物理等效电路模型，结果表明，温度和电流对电池参数的影响明显。Yu等［11］将放电过程分为3个阶段，采用粒子群优化算法和粒子滤波算法进行参数辨识、参数更新和RDT预测。文献［12］中还提出了一种狄利克雷过程混合模型和粒子滤波相结合的方法来预测RDT。Dong等［13］以过去电流信息为根据，预测未来电流，进一步结合等效电路模型预测RDT。程树英等［14］提出了一种基于模糊信息粒化的支持向量回归方法，用于预测锂电池RCT。国内外针对电池的研究已经取得了很多成果，但结合平流层飞艇的实际工况对电池进行研究还鲜见相关文献资料。特别是充电过程，通常情况下充电过程是恒流或恒压条件，而平流层飞艇的充电过程受到太阳辐照、飞行姿态等因素的影响，电流是不断变化的。

本文先建立了平流层飞艇能源系统模型。然后，进行了锂电池的充放电测试，采用多项式拟合测试数据，建立了量化计算SOC、RDT和RCT的储能电池模型。最后，通过模拟飞行试验验证了储能电池模型的计算精度，可为制定飞行策略提供量化支撑。

1 能源系统模型

平流层飞艇的能量传递过程如图1所示，包括能量输入、能量消耗、能量存储3部分。能量输入部分即太阳辐照抵达太阳能电池阵列表面后，辐照能量被转化为电能输出；能量消耗部分包括推进电机和其他耗电设备的能量消耗；能量存储部分即储能电池存储和释放能量。当太阳能电池阵列输出功率大于飞艇总消耗功率时，多余的电能将被存储在储能电池中，当太阳能电池阵列输出功率小于飞艇总消耗功率时，储能电池将释放电能，使能量供需平衡［15］。

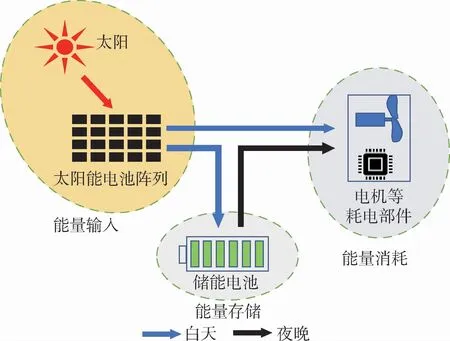
图1 平流层飞艇能量传递示意图Fig.1 Schematic diagram of energy transfer in a stratospheric airship

1.1 能量输入模型

太阳辐照包括直射、反射和散射。由于平流层在云层之上，且太阳能电池阵列布置在飞艇顶部，因此，平流层飞艇太阳能电池阵列接收到的辐照强度F由散射辐照强度Fh和直射辐照强度F0构成［16］：

根据文献［6］，考虑到飞艇外形为椭球型，不同位置太阳辐照的入射角不同，辐照强度也不同，因此，将太阳能电池阵列分割成n0×m0个微元，所有微元接收的辐照强度总和即为电池阵列接收的辐照强度。每个微元接收的辐照功率Pnm可表示为

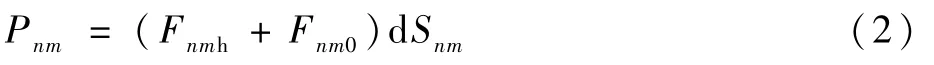
式中：n为周向坐标；m为轴向坐标；Fnmh为微元散射辐照强度；Fnm0为微元直射辐照强度；d Snm为微元面积。微元散射辐照强度可表示为

式中：βnm为微元平面与水平面之间的夹角。微元直射辐照强度可表示为

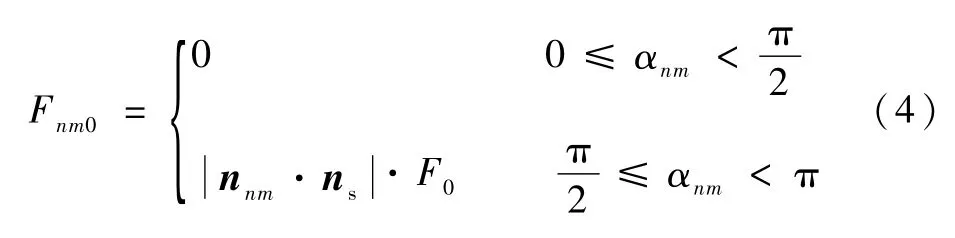
式中：nnm为微元单位法向量；ns为单位辐照强度矢量；αnm为nnm和ns的夹角。

单晶硅太阳能电池效率与温度之间的经验公式为［17］

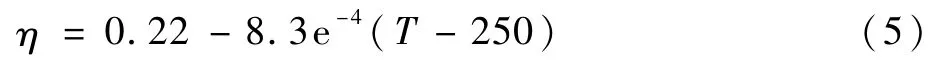
式中：T为温度。

1.2 能量消耗模型

飞艇总消耗功率由推进功率和其他功率组成：

式中：Pelse为推进系统之外的其他系统消耗的功率，其值比较稳定，受飞行速度、飞行姿态等影响小；Pprop为推进系统消耗的功率，可表示为

式中：ηprop为螺旋桨效率；ηmot为推进电机效率；vair为飞艇空速；FT为飞艇推力。

2 储能电池模型

长航时平流层飞艇通过储能电池不断进行充放电循环来实现夜间飞行状态的维持，因此，实时掌握电池的SOC、RDT和RCT是制定飞行策略和优化能源利用的关键。电池充放电过程是复杂的电化学过程，电池在使用过程中，SOC、RDT和RCT受到诸多因素的影响，其中受电流倍率和温度的影响较大［18］。平流层飞艇通常会对储能电池采取控温措施，使电池温度恒定在一定范围内，因此本文未考虑温度的影响。

2.1 试验设置

本文以松下NCR18650B型锂电池为测试对象，具体参数如表1所示，进行了不同电流倍率下的充放电测试，对测试数据进行了分析和多项式拟合，分别建立了充放电状态下的SOC、RDT和RCT量化计算模型。

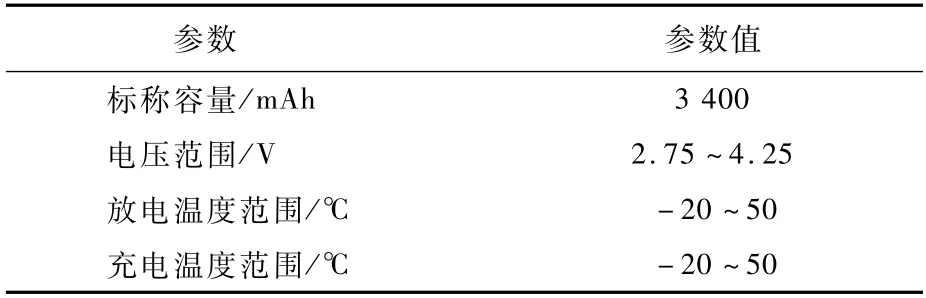
表1 测试电池的基本参数Table 1 Basic parameters of test batteries

试验中所用松下NCR18650B型锂电池的标称容量并非实际容量，实际容量会因电流倍率不同而变化。试验平台如图2所示。充电时，电池正负极分别与稳压直流电源的正负极接通；放电时，电池正负极分别与电子负载的正负极接通。电压采集模块的采集频率为60 Hz。监控PC用于显示和保存采集数据。电池放置在温度环境试验箱内，测试过程中温度设置为25℃，实际温度范围为24.7～25.3℃。

图2 充放电测试示意图Fig.2 Schematic diagram of charging and discharging test

充电和放电测试均采用恒流模式，放电采用9种不同倍率的电流（0.05C、0.1C、0.15C、0.2C、0.25C、0.3C、0.35C、0.4C、0.5C），截止电压为2.75 V。充电采用6种不同倍率的电流（0.05C、0.1C、0.15C、0.2C、0.25C、0.3C），最大电压为4.25 V，截止电流为0.01C。

2.2 数据分析与建模

2.2.1 放电数据分析与建模

1）放电SOC量化计算模型

放电时端电压与SOC的关系如图3所示。同一电流倍率下，不同SOC对应不同端电压；不同电流倍率的曲线不重合，电流倍率越大，曲线越靠下。当电流倍率和端电压确定后，即可确定此时的SOC，可以根据这一方法实现对SOC的实时计算。

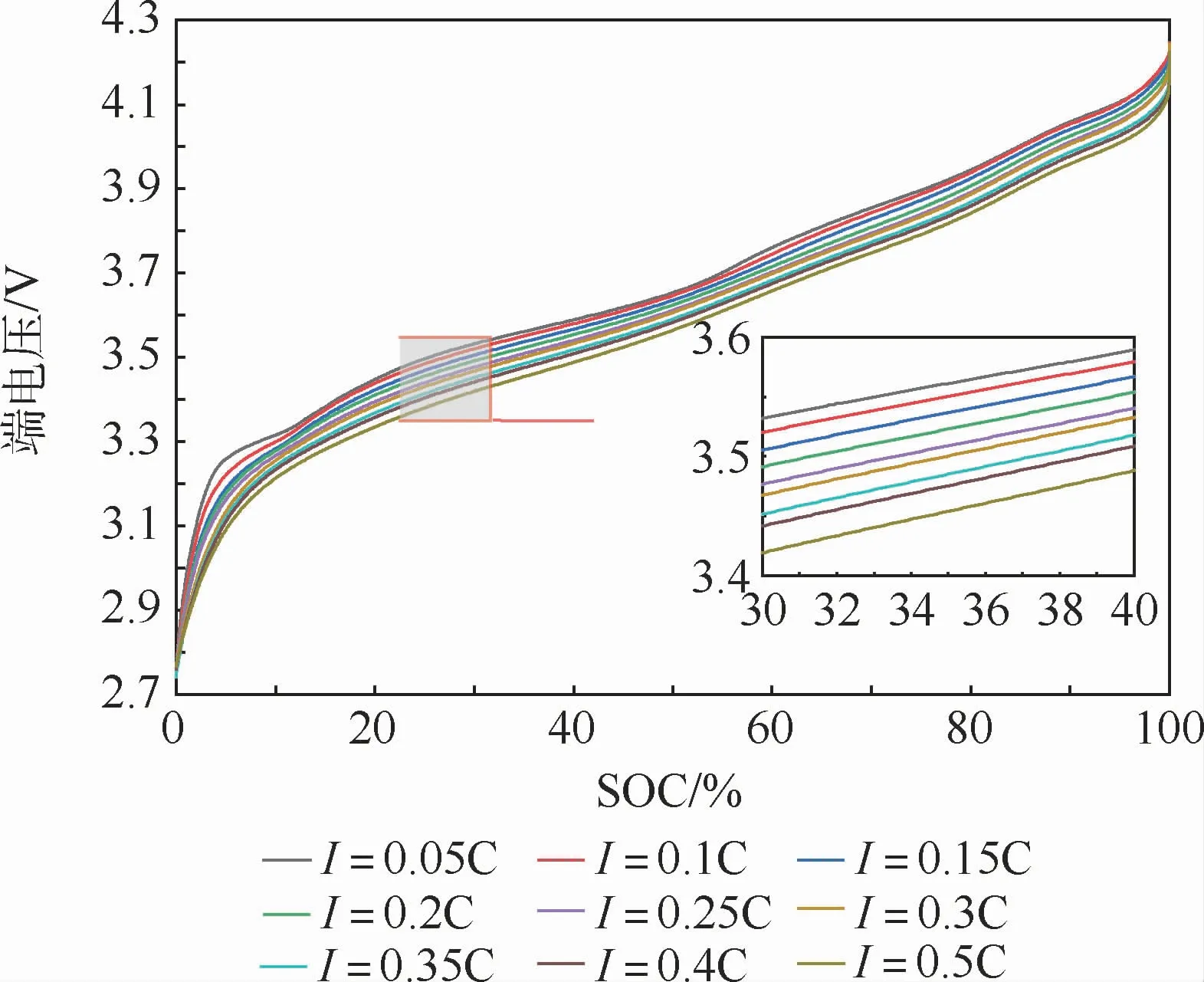
图3 不同电流倍率放电时端电压与SOC的关系Fig.3 Relationship between terminal voltage and SOC at different discharging rates

具体方法如下：按5%SOC为步长，从100%～5%中取20个值，5%以下取3%、2%、1%、0%四个值，因为SOC接近0%时，电池端电压变化十分剧烈，减小步长可以减小拟合误差。每一电流倍率一共有24组数据（包括SOC和端电压），以端电压为自变量，SOC为因变量，进行多项式拟合。经过多次对比，发现按8次多项式拟合可得到最佳的拟合曲线为

式中：Aji表示电流倍率为i时，j次项的系数；Vi为i对应的端电压。拟合结果如图4所示。

图4 SOC与端电压的8次多项式拟合Fig.4 Fitting of eighth-degree polynomial between SOC and terminal voltage

将系数Aji与电流倍率按式（9）进行拟合，拟合所得一次项系数Bj1和常数项Bj0的结果如表2所示。

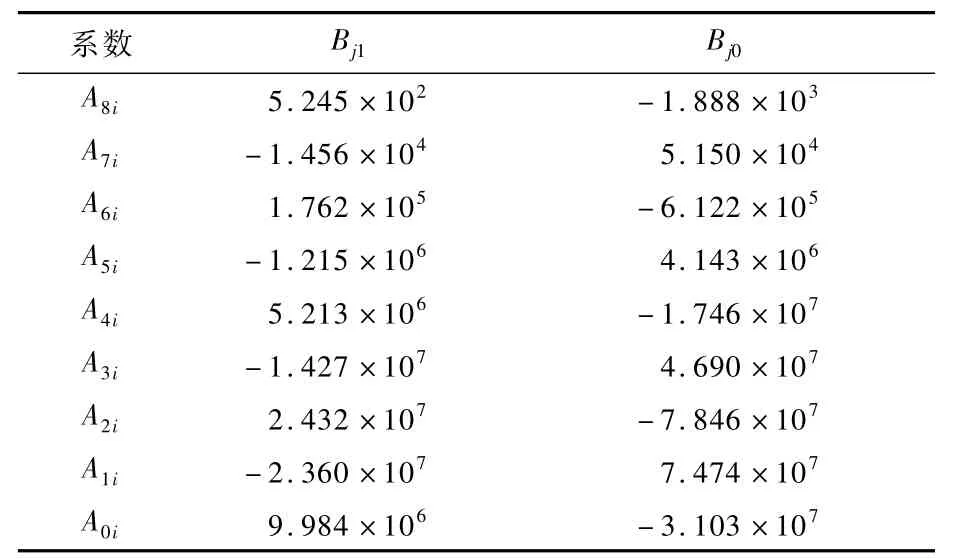
表2 线性拟合8次多项式系数与电流倍率的结果Table 2 Results of linear fitting of eighth-degree polynomial coefficients and discharging rate

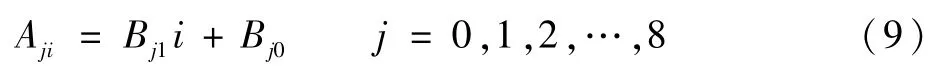
通过如上分析，当电池放电时，已知电流倍率和端电压，即可通过式（8）和式（9）求得当前条件下准确的SOC值。

2）放电RDT量化计算模型

电池放电容量与电流倍率相关，如图5中测试数据点所示。因此，当电流倍率变化时，要准确反应电池的放电特性，则必须要考虑不同电流倍率对电池容量的影响，而不能用标称容量或某个常数。线性拟合放电容量与电流倍率，其相关系数为0.983，说明放电容量与电流倍率之间具有很强的线性关系：

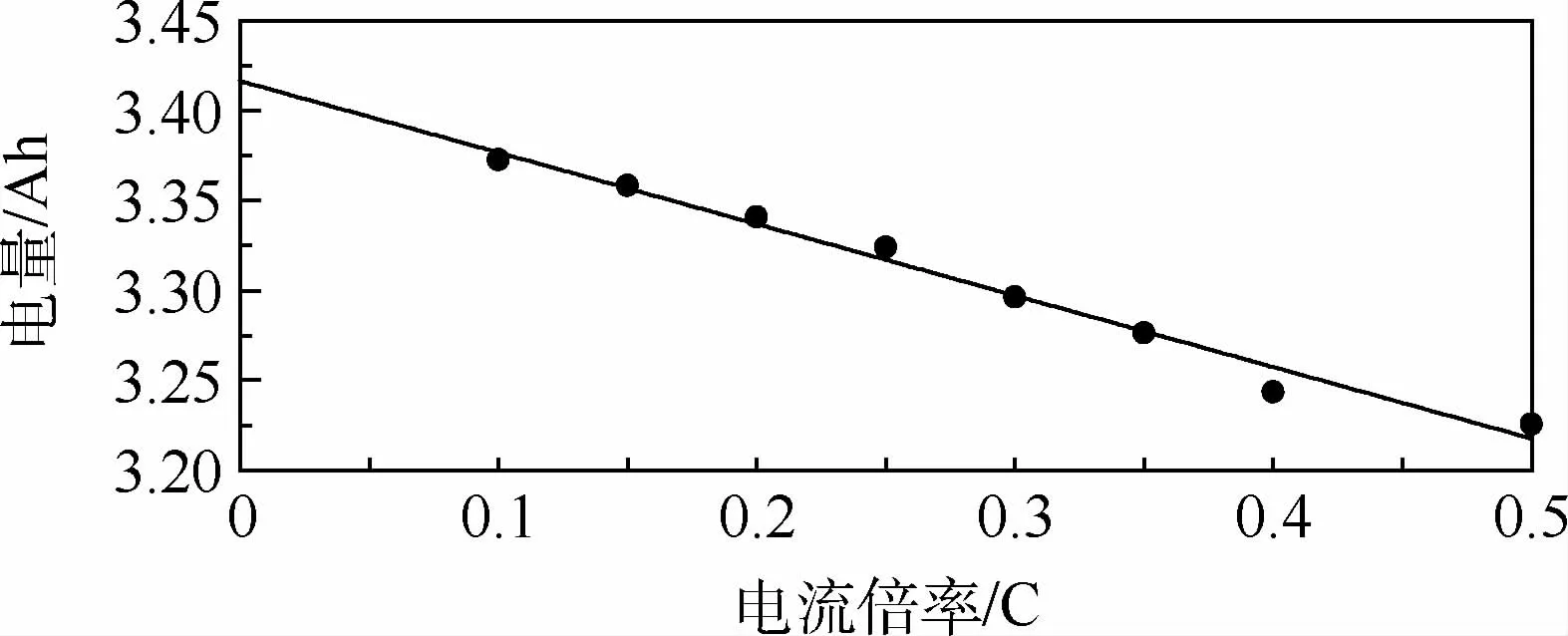
图5 放电容量与电流倍率线性拟合Fig.5 Linear fitting between discharging capacity and discharging rate

式中：Q0i为电流倍率i对应的放电容量；k=-0.397 5；b=3.416。

如图6所示，电流倍率越大，总放电时间越短。对于恒流放电，放电容量、电流倍率、总放电时间之间满足如下关系：

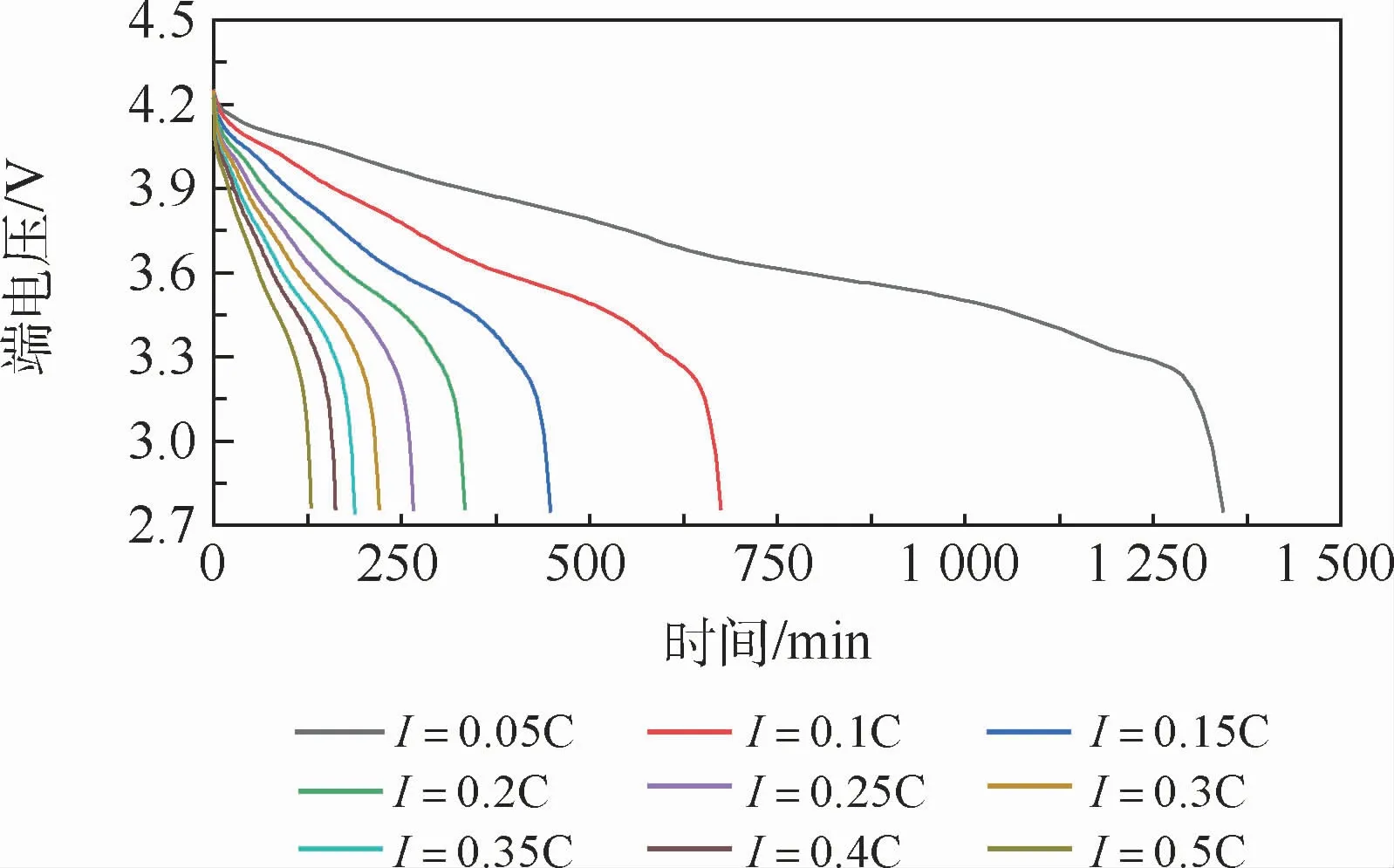
图6 不同电流倍率端电压与放电时间的关系Fig.6 Relationship between terminal voltage and discharging time at different discharging rates

式中：T0i为电流倍率i对应的总放电时间；I为电流；Cm为标称容量。结合式（10）和式（11）可得

按式（12）拟合总放电时间T0i与电流倍率i得k=-0.382 5，b=3.414。如图7所示，T0i与1/i具有很强的线性关系，且k值和b值与按式（10）拟合所得值非常接近（k相差3.8%，b相差0.6%），说明2次拟合是准确的。

图7 放电时间与电流倍率拟合Fig.7 Fitting between discharging time and discharging rate

对于恒流放电，电流倍率始终恒定，以电流I放电，则t时刻RDT可表示为

式中：Qti为t时刻电池剩余电量；Q0i是电池的总放电容量；SOCt为t时刻的SOC；不同电流倍率恒流放电的总放电时间T0i如表3所示。

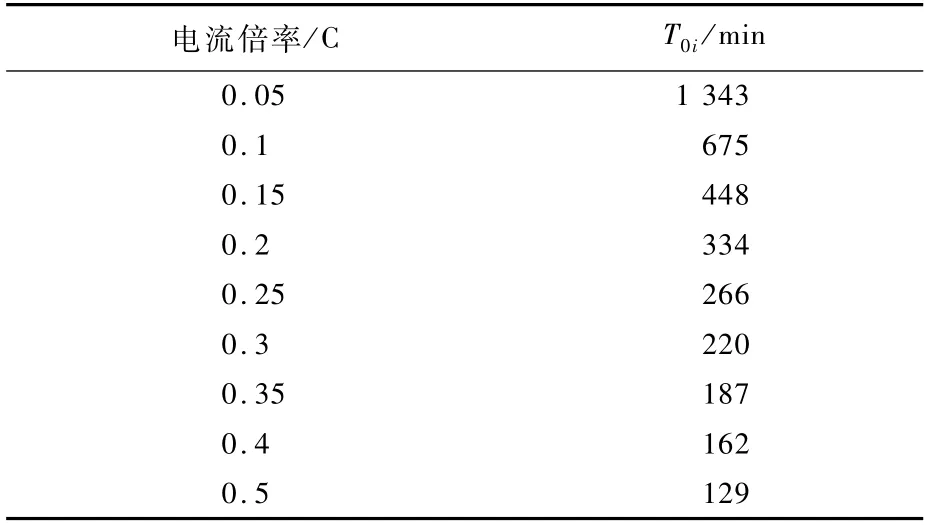
表3 不同电流倍率恒流放电的总放电时间Table 3 Total duration of constant-current discharging at different discharging rates

2.2.2 充电数据分析与建模

充电过程在电化学反应上是放电过程的逆过程，但是具体参数的变化规律却与放电过程有很大不同。本文将充电过程分为3个阶段进行研究，即快速升压段、缓慢升压段和恒压段。图8为恒流充电时端电压与SOC的关系。当电池电压很低时，电池端电压会迅速上升，直至某一电压值后，端电压开始缓慢地上升，定义电压上升速率的转变点为临界电压，电流倍率不同，临界电压也不同；当端电压上升至电池最大电压（4.25 V）后，则转为恒压充电，电流倍率会逐渐减小，减小至0.01C时，视为电池充满电，SOC=100%。

图8 不同电流倍率充电时端电压与SOC的关系Fig.8 Relationship between terminal voltage and SOC at different charging rates

临界电压前称为快速升压段，端电压达到最大电压后称为恒压段，介于2段中间称为缓慢升压段。本小节将对这3个阶段分别进行分析与建模。

1）快速升压段

快速升压段的持续时间和充电容量占整个充电过程的比例很小，如表4所示。电池处于快速升压段时，离充电结束还有很长时间，此时电池的SOC和RCT对能源系统的参考意义较弱。综合以上因素，本文对快速升压段的模型进行简化，即SOC=0，RCT为无穷大。

表4 快速升压段充电时间与充电容量所占百分比Table 4 Percentage of charging time and charging capacity at the stage of voltage rising rapidly

2）缓慢升压段

缓慢升压段持续时间最长的，如图8缓慢升压段所示，同一电流倍率下，不同SOC对应不同端电压；不同电流倍率的曲线不重合，电流倍率越大，曲线越靠上。当电流倍率和端电压确定后，即可确定此时的SOC，可以根据这一方法实现对SOC的实时计算。根据端电压变化的特点，本文采用二次多项式（式（14））对SOC和端电压进行拟合，拟合结果如图9所示。

图9 缓慢升压段SOC与端电压的拟合Fig.9 Fitting between SOC and terminal voltage at the stage of voltage rising slowly

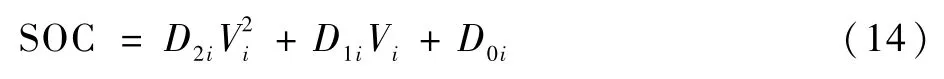
式中：D2i、D1i和D0i分别为二次项系数、一次项系数和常数项。

将系数D2i、D1i、D0i分别与电流倍率进行拟合：

拟合结果如表5所示。

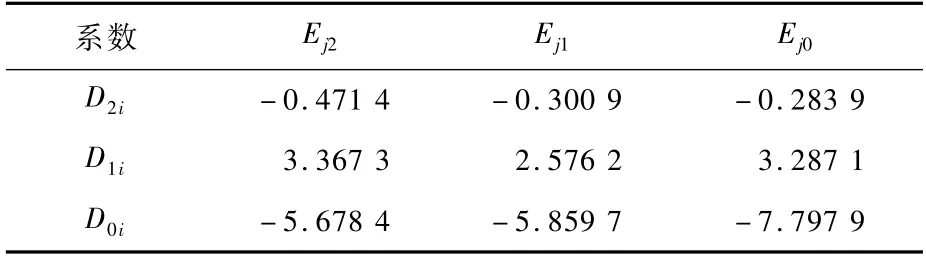
表5 缓慢升压段多项式系数与电流倍率拟合的结果Table 5 Fitting results of polynomial coefficients and charging rates at the stage of voltage r ising slowly

综上，对于充电过程的缓慢升压段，已知电流倍率和端电压，根据式（14）和式（15）即可求得当前条件下的SOC。

对缓慢升压的RCT和端电压测试数据按式（16）进行拟合，如图10所示，电流倍率越大，RCT的斜率越大，不同电流倍率的曲线不重合，因此，与计算缓慢升压段的SOC类似，也可以通过电流倍率和端电压确定当前条件下的RCT。

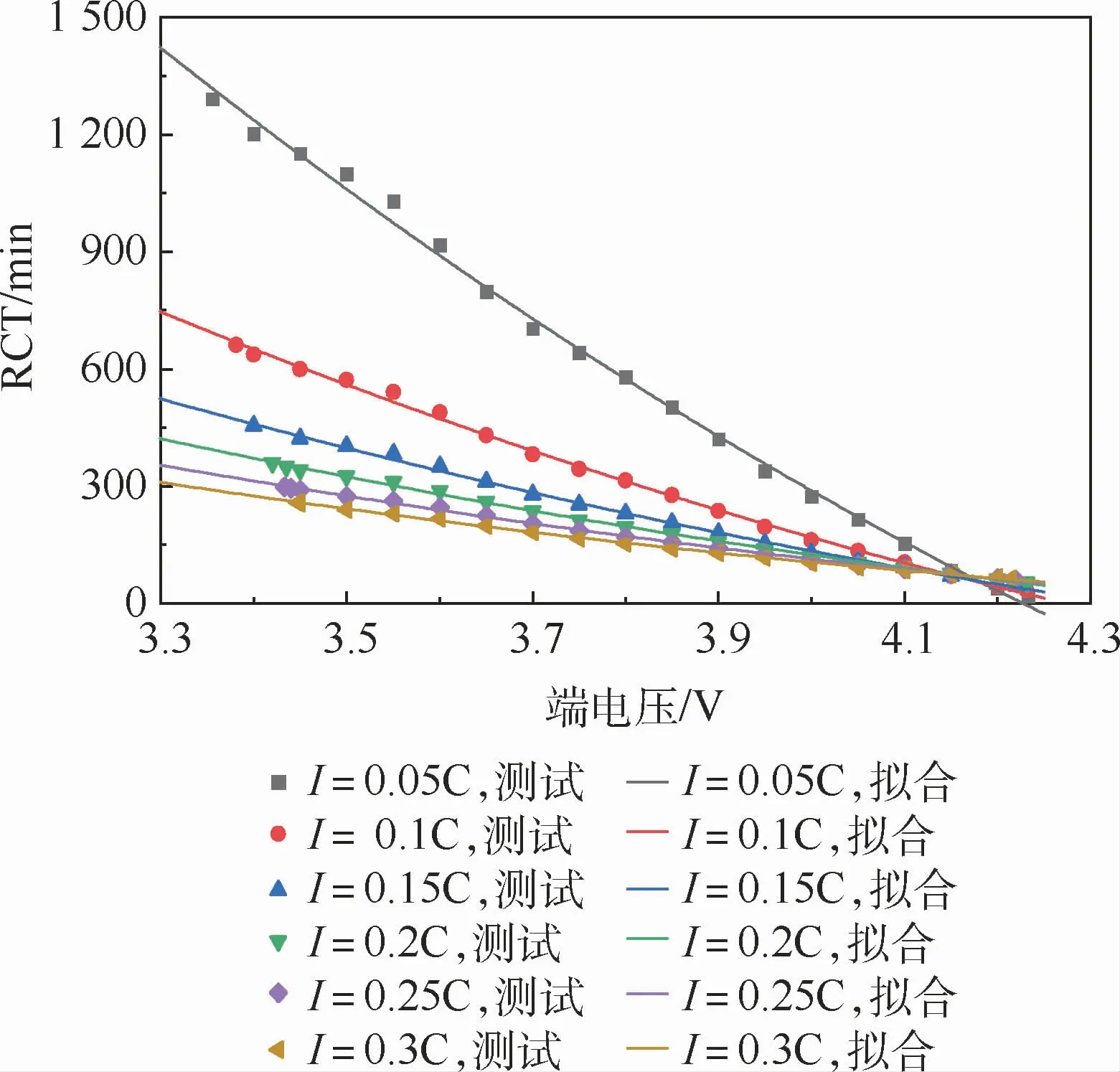
图10 缓慢升压段RCT与端电压的拟合Fig.10 Fitting between RCT and terminal voltage at the stage of voltage rising slowly

式中：Vi为电流i对应的端电压；G2i、G1i和G0i分别为二次项系数、一次项系数和常数项。

将系数G2i、G1i、G0i分别与电流倍率进行拟合，拟合公式为

拟合结果见表6。对于充电过程的缓慢升压段，已知电流倍率和端电压，根据式（16）和式（17）即可求得当前条件下的RCT。

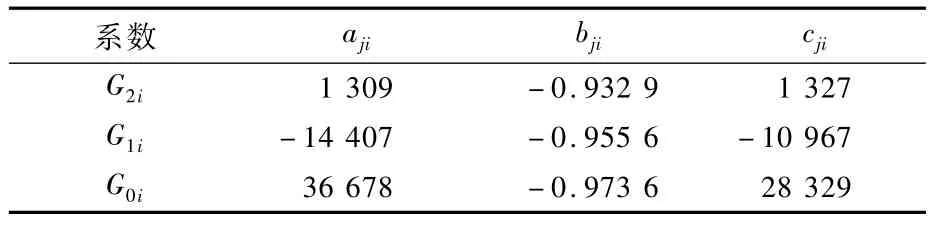
表6 缓慢升压段系数pjI与电流倍率拟合结果Table 6 Fitting results of coefficient pjI and charging rates at the stage of voltage rising slowly

3）恒压段

当充电过程进入恒压段以后，电池端电压基本保持恒定，但是电流倍率会越来越小，恒压段的充电容量和持续时间与缓慢升压段的电流倍率有关，如图11和图12所示。恒压段充电量虽然不多，但是处于充电末期，此时的SOC和RCT对能源系统具有很强的参考意义。恒压段的各条SOC曲线、RCT曲线之间重合度很高，为简化模型，本文取0.3C恒流充电的SOC曲线和RCT曲线作为典型曲线，替代其他电流下的曲线。拟合后得到

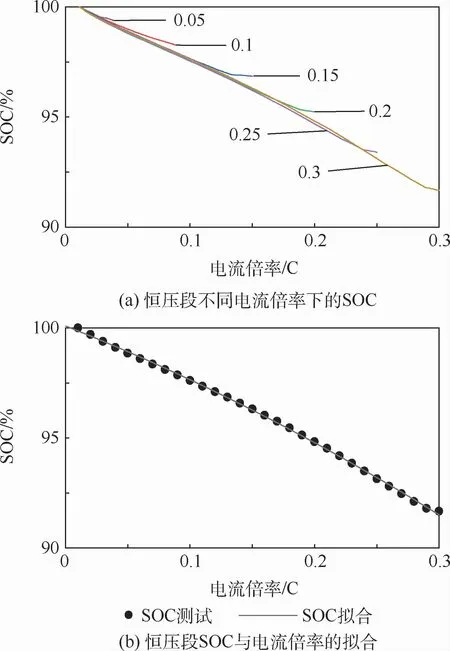
图11 恒压段SOC与电流倍率的关系Fig.11 Relationship between SOC and charging rates at constant voltage stage

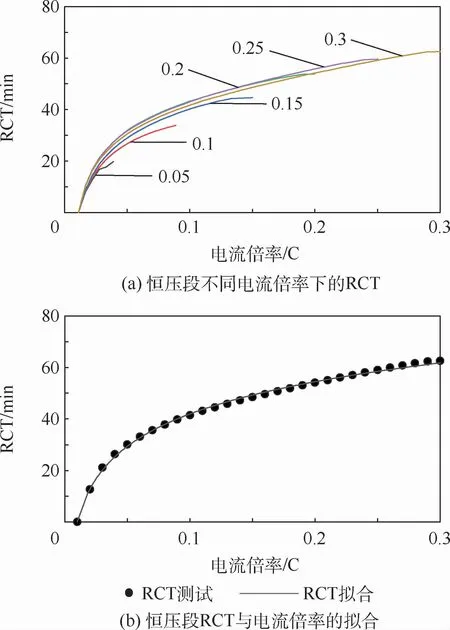
图12 恒压段RCT与电流倍率的关系Fig.12 Relationship between RCT and charging rates at constant voltage stage

对于恒压段，可通过当前电流倍率计算SOC和RCT。

综上所述，每采集一组电压、电流数据，即可通过储能锂电池模型对SOC、RDT、RCT进行更新，且计算结果与历史采集数据和历史计算结果无关，因此，该模型对历史数据和SOC、RDT、RCT初值不具有依赖性，任意设定初始值，该模型经过一步计算即可收敛至参考值。

3 模型验证

为了验证本文所建立的储能电池模型的准确性，开展了模拟飞行试验。

3.1 参数和方案

本文根据平流层飞艇的实际飞行环境和飞行任务，利用能量输入模型和能量消耗模型对平流层飞艇的能量输入和消耗情况进行了仿真和分析，将仿真结果转化为单体电池的充放电过程，利用本文建立的储能电池模型计算电池的SOC、RCT和RDT。平流层飞艇的主要参数根据参考文献［6］和文献［19］确定，具体参数如表7所示。

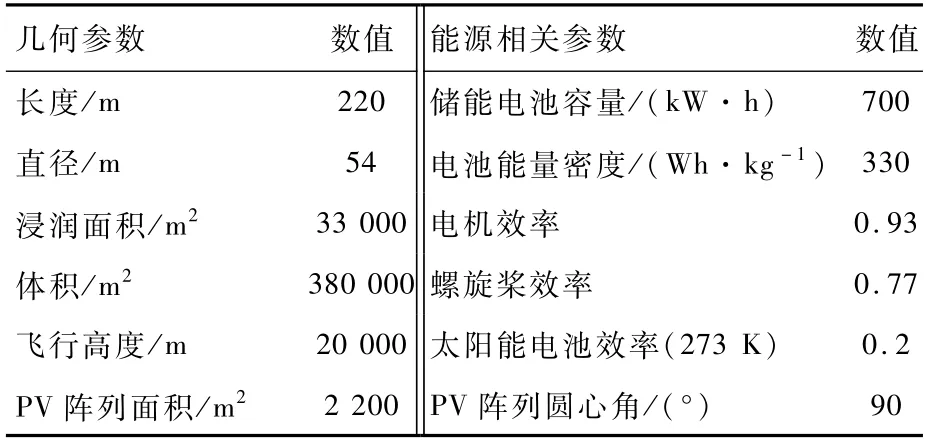
表7 飞艇参数Table 7 Airship parameters

由于目前太阳能电池的转化效率和储能电池的比能量都较低，为了保证平流层飞艇有足够的能量，选定仿真日期为辐照强度最高的夏至日，仿真地点为三亚地区。本文对2个飞行方案进行了仿真，方案参数设置如表8所示。

表8 两个飞行方案的参数设置Table 8 Parameter setting for two flight schemes

在长航时飞行过程中，能源系统以24 h为周期不断循环，为方便试验操作，以电池充满电后由静置状态转为放电状态时为试验起点，根据能源系统模型仿真结果（见图13），初始时刻为18：00。

图13 飞艇各部分能量情况（方案A）Fig.13 Energy conditions of each part of airship（Plan A）

3.2 试验结果分析

本节对方案A进行仿真和分析。通过能量输入和能量消耗模型对方案A进行仿真，得到飞艇的平均辐照强度、总消耗功率、太阳能电池阵输出功率和剩余功率，如图13所示。当剩余功率大于0时，剩余功率为储能电池的充电功率，当剩余功率小于0时，剩余功率为储能电池的放电功率。

实际飞行过程中，太阳辐照随时间连续变化，剩余功率也连续变化。试验所用设备不具备输出连续变化电流的功能，所以将电池的充放电过程按能量守恒原则，即以10 min为步长，将充放电电流倍率离散，离散后单体电池充放电功率和电流倍率如图14所示。

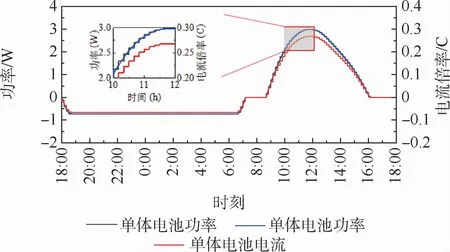
图14 充放电功率和电流（方案A）Fig.14 Charging and discharging power and current（Plan A）

按照图14所示的电流曲线，对电池进行模拟飞行充放电试验，图15展示了方案A的电池端电压、电流倍率、SOC、RDT和RCT随时间变化的曲线。每个循环（24 h）可按表9所示分为7个阶段：

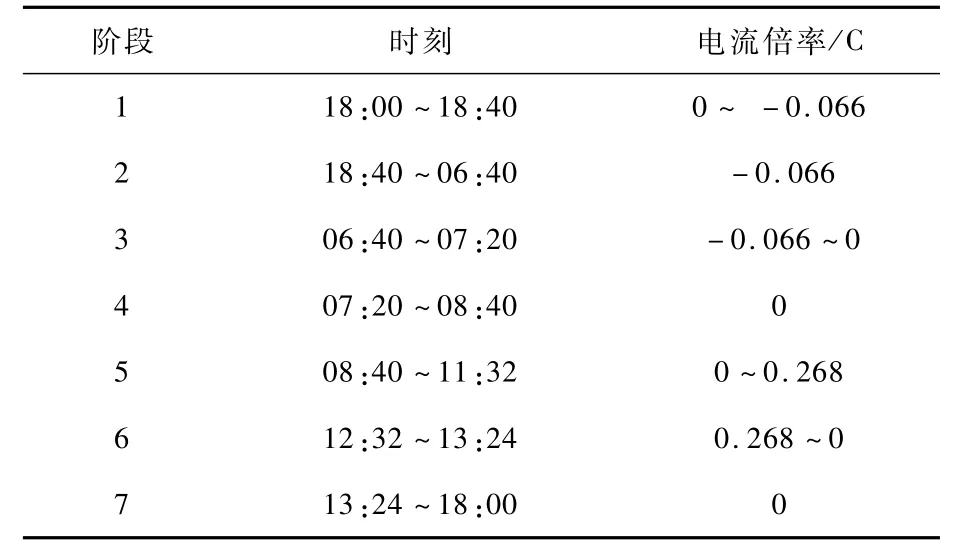
表9 储能电池工作阶段划分（方案A）Table 9 Work stage division of energy stor age battery（Plan A）

图15 模拟飞行试验结果（方案A）Fig.15 Simulated flight test results（Plan A）

第1阶段，电池变电流放电，电流倍率从0逐渐变到-0.066C，端电压、SOC和RDT都在减小。每10 min电流改变一次，RDT也随之发生较大改变，因为RDT表示按照当前电流放电的剩余放电时间，因此，放电电流变大，剩余放电时间会随之变小。

第2阶段，电池恒流放电，端电压、SOC和RDT都在稳定地减小。SOC和RDT都近似匀速减小，说明该储能电池模型在估算SOC和RDT时是稳定且准确的。

第3阶段，电池放电电流逐渐减小至0，SOC仍然在继续减小，而端电压先减小后回升，这是因为当放电电流接近0时，电池欧姆内阻电压和极化电阻电压减小明显，使端电压升高。RDT则随着每次电流减小而变大，其原因同第1阶段中所述。

第4阶段，电池电流倍率为0，电池静置。静置的初始阶段，端电压仍在缓慢上升，这是电池的极化效应所致；电流减至0后，极化电阻电压需要一定时间才能降为0，而电池端电压会随着极化电阻电压降低而缓慢升高。

第5阶段，电池充电，电流倍率从0逐渐增加。端电压开始上升，至本阶段末端时达到最大电压。RCT不断减小，表示剩余充电时间减小，并且随着充电电流的减小，RCT的斜率也不断减小。

第6阶段，电池恒压充电，电流减小至0.01C，由于电流迅速减小，SOC上升斜率也迅速减小，最后达到100%，RCT最终降为0。

第7阶段，电池处于满电状态，静置至下一个循环开始。

一个完整的循环过程中，SOC误差小于3%，RDT误差小于1.5%，RCT误差在充电初始时刻略大，但很快降低并维持在1.5%以内。充电初始时刻距离充满电还有很长时间，短时间出现稍大一点的误差对整个循环过程的估算精度没有明显影响，对制定飞行策略也没有明显影响。在1～3放电阶段，SOC计算误差在3%以内波动；在5～6充电阶段，SOC误差在波动中逐渐减小；在充满电后，校准SOC，误差为0。

方案B的结果如表10和图16所示，各阶段的参数变化规律与方案A大同小异，本文不再赘述。方案B的SOC误差小于3%，RDT误差小于1.5%，RCT误差在充电初始时刻为2.5%，但迅速降低并维持在1.5%以内。2个方案的仿真和试验结果均表明该储能电池模型具有很好的计算精度，满足平流层飞艇实际应用需求。

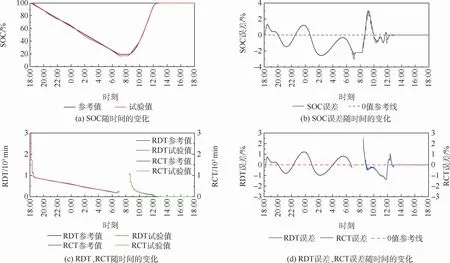
图16 模拟飞行试验结果（方案B）Fig.16 Simulated flight test results（Plan B）

表10 储能电池工作阶段划分（方案B）Table 10 Wor k stage division of energy storage batter y（Plan B）

4 结论

本文根据电池充放电试验数据，采用多项式拟合的方法建立了储能电池模型，并进行了模拟飞行试验分析，结果表明：

1）能源系统模型可对平流层飞艇的能量输入和消耗进行仿真分析，并能输出储能电池的功率曲线，可为模拟飞行试验提供依据。

2）本文所构建储能电池模型可同时对SOC、RDT、RCT进行在线计算，为制定飞行策略和优化能源利用提供量化支撑。

3）本文所构建储能电池模型的SOC计算误差小于3%，RDT计算误差小于1.5%，RCT计算误差除充电初始时刻略大，稳定后维持在1.5%以内。

4）本文所构建储能电池模型对历史数据和初始值不具有依赖性，任意设定初始值，该模型经过一步计算即可收敛至参考值。