基于信息融合和广义循环互相关熵的电机轴承故障诊断
李 辉, 郝如江
(1.天津职业技术师范大学 机械工程学院,天津 300222; 2.石家庄铁道大学 机械工程学院,石家庄 050043)
滚动轴承广泛应用于各种类型电机中,其健康状态对保证电机的正常运转具有重要作用[1]。在电机轴承故障检测与诊断中,常常采用基于振动信号处理的方法[2]。但在采集得到的振动信号中,不仅包含大量的高斯和非高斯噪声,而且还呈现一定的非线性[3]。为得到可靠的诊断效果,往往需要对传感器采集的信号进行降噪处理,如卡尔曼滤波、共振稀疏分解[4]、最大相关峭度解卷积[5]和经验模态分解[6]等,而这些方法在处理非线性、非高斯噪声信号时,会造成性能衰退甚至失效[7]。基于信号高阶统计量的方法[8-9],虽然对高斯噪声具有免疫能力,但也难以有效抑制强脉冲噪声,而且高阶统计量计算方法复杂且计算量大,限制了高阶统计量的实际应用和推广。近年来,在通信领域,基于信号分数低阶统计量[10-12]( fractional lower-order statistics, FLOS)和相关熵[13-15](Correntropy)的方法得到了广泛应用,在非高斯、非线性信号处理方面取得了较好的效果。相关熵是处理脉冲噪声的有效方法,已在雷达和通信信号检测、信号滤波、波达方向估计和时延估计等方面得到应用和验证,取得了良好效果[16-18],其性能优于FLOS。相关熵采用高斯核函数,高斯核函数只有一个核长调整参数,只能调整高斯概率密度曲线的方差,而不能调整其“钟形”形态,因而自适应性较差。为改善相关熵的性能,2016年,Chen等[19]以广义高斯分布函数作为核函数,提出了广义相关熵的概念,广义高斯分布函数具有形状和核长两个参数,因而具有更好的适应性,已在通信信号自适应滤波方面取得了良好效果[20-21],但还未在机电设备故障诊断领域得到应用。本文将多传感器信息融合[22]、广义相关熵与循环平稳信号处理方法相结合,提出了基于信息融合和广义循环互相关熵的轴承故障诊断方法,并用仿真信号和电机轴承内圈、外圈局部裂纹故障试验信号对提出方法进行了验证,信号仿真和试验结果表明:本文提出的方法具有很强的降噪能力,为电机轴承故障检测和诊断提供了一种有效方法。
1 广义循环互相关熵
1.1 广义高斯分布
广义高斯分布(generalized gaussian distribution, GGD)函数定义为[23]
(1)
式中,Γ(·)是Γ函数,即

(2)
(3)
式中,σ为方差。
GGD共有两个参数:p是形状指数(p>0),控制着概率密度函数的“形状”,即衰减的速度;σ为方差(核长,σ>0)。
1.2 广义互相关熵
对于任意两个实随机变量x和y(x,y∈R),它们的广义互相关熵可定义为
Vp,σ(x,y)=E[κp,σ(x,y)]
(4)
式中:E[·]为期望算子;κp,σ(·)为由式(1)定义的广义高斯核函数,即
(5)
式中,‖·‖为范数算子。

(6)
实随机过程x(t)和y(t)(t∈R)的时变广义互相关熵(cross correntropy)可表示为
(7)
式中,τ为时间滞后量。
1.3 广义循环互相关熵和谱密度

(8)
(9)
在式(9)中,当α=0时,广义循环互相关熵谱密度退化为传统的功率谱密度。
2 基于信息融合的广义循环互相关熵轴承诊断方法
利用两个传感器,采集两路振动信号x(t)和y(t),并对两路信号进行解卷积,以消除传递路径的影响,然后计算两路解卷积后振动信号的广义循环互相关熵谱密度,最后根据互相关熵谱识别轴承故障。其方法步骤如下:
步骤1采集两路振动信号x和y;
步骤2对振动信号x和y进行解卷积预处理;


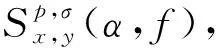
3 信号仿真
滚动轴承点蚀故障振动响应信号模型可以表示为[24-25]
(10)
式中:Ai为瞬态脉冲幅值;T为脉冲周期;τi为第i次冲击相对于脉冲周期T的微小波动;n(t)为平稳随机噪声。
对于式(10)所示的滚动轴承点蚀故障振动响应信号模型,瞬态冲击s(t)是以系统的固有频率fb为频率的振荡衰减信号。假定模拟轴承外圈故障振动响应信号,此时Ai为常数,式(10)可具体描述为
(11)
x(t)=x1(t)+n1(t)+n2(t)
(12)
式中:Ai为瞬态脉冲幅值;Ci为阻尼衰减因子;ti为冲击持续的时间;θbi为初始相位;fbi为电动机系统的共振频率;n1(t)为零均值高斯噪声;n2(t)为脉冲噪声。
函数Θ(t-ti)用来指定冲击发生的时间,可用式(13)定义
(13)
设轴承外圈故障特征频率为fo=110 Hz,电动机系统的固有振动频率fb=1 000 Hz,瞬态冲击振幅Ai=5,采样频率fs=6 000 Hz。
信号仿真的目的主要有2个方面,首先通过式(11)表示的未加任何噪声的轴承外圈仿真信号,验证广义循环互相关熵的频谱特征,为轴承故障诊断奠定基础;其次通过式(12)的仿真信号,验证广义循环互相关熵的降噪性能。
3.1 广义循环相关熵频谱特征仿真
图1(a)是式(11)表示的仿真信号的时域波形,图1(b)是其FFT,从图1(b)中可以看出,以系统的固有频率1 000 Hz为中心,两边分布着以轴承外圈故障特征频率fo=110 Hz为间隔的边频带。
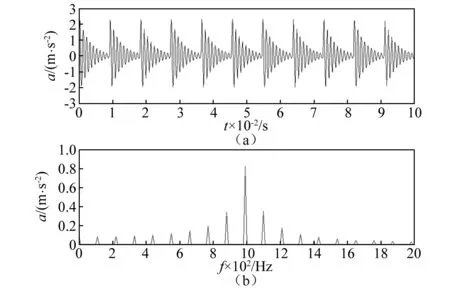
图1 轴承外圈故障仿真信号Fig.1 Simulative signal for bearing with outer race fault
图2、图3分别为轴承外圈故障仿真信号广义循环相关熵函数的二维和三维图,从图2和图3中可以清楚地观察到信号的循环频率信息分布在循环频率域的低、高两个不同的频率段,低频段的循环频率对应轴承外圈故障频率fo及其倍频;高频段的循环频率是以二倍的载波频率(α=2 000 Hz)为中心、以轴承外圈故障特征频率fo为间隔的边频带。因此,根据广义循环相关熵函数可以准确识别轴承故障。

图2 广义循环相关熵(Contour图)Fig.2 Generalized cyclic correntropy of simulative signal (Contour plot)

图3 广义循环相关熵(三维图)Fig.3 Generalized cyclic correntropy of simulative signal (3D plot)
图4和图5分别为仿真信号广义循环相关熵谱密度函数的二维和三维图,在图4中存在着许多独立的谱峰,这些谱峰主要分布在f=0.5α和f=-0.5α两条频谱线及其平行线上;在频谱中心(0,0)和2倍共振频率处(±2 000,±1 000),这些平行线构成菱形,菱形在水平方向的对角线长度等于2fo,在垂直方向的对角线长度等于fo,这种频谱结构,清晰表达了轴承外圈故障频谱特征,因此,根据这些频谱特征可准确识别轴承故障。

图4 广义循环相关熵谱密度(Contour图)Fig.4 Generalized cyclic correntropy spectral density of simulative signal (Contour plot)

图5 广义循环相关熵谱密度(三维图)Fig.5 Generalized cyclic correntropy spectral density of simulative signal (3D plot)
3.2 广义循环相关熵降噪性能仿真
首先在轴承外圈故障仿真信号x1(t)中加入零均值高斯噪声n1(t),信噪比为SNR=-3 dB,之后再随机加入几个幅值不同的脉冲信号,以模拟脉冲噪声。图6(a)为式(12)表示的仿真信号时域波形,从图6(a)可以看出,仿真信号完全被噪声淹没,因此从图6(a)已完全看不出信号幅值的变化规律。图6(b)为其FFT,在图6(b)中也不能有效识别信号的频率成分。
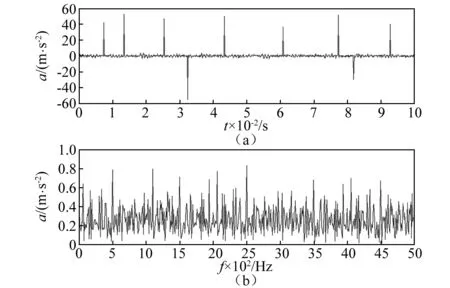
图6 轴承外圈故障仿真信号Fig.6 Simulative signal for bearing with outer race fault
含噪声仿真信号的广义循环相关熵谱密度(p=3,σ=0.6),如图7(为清晰看出频谱结构,仅画出了频谱中心部分)和图8所示。在图7和图8中可以清晰看出:在循环频率σ和谱频率f构成的双频平面内,含噪声仿真信号的能量主要分布在f=0.5α和f=-0.5α等两条频谱线上,谱峰幅值较大;由于噪声的存在,在f=0.5α±1 000和f=-0.5α±1 000等四条谱线上也存在谱峰,但幅值较小,由这四条谱线形成较大的菱形,大菱形在水平方向的对角线长度等于2fb,在垂直方向的对角线长度等于fb,这种频谱准确表达了系统的共振频率fb。通过上述分析表明:广义循环相关熵谱具有很强的能量聚集性,能准确表示强噪声中信号的频率成分,能有效抑制高斯噪声和非高斯脉冲噪声。
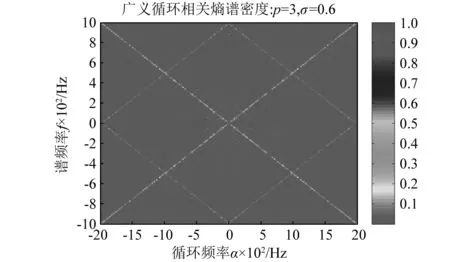
图7 广义循环相关熵谱密度(Contour图)Fig.7 Generalized cyclic correntropy spectral density of simulative signal (Contour plot)

图8 广义循环相关熵谱密度(三维图)Fig.8 Generalized cyclic correntropy spectral density of simulative signal (3D plot)
为凸显广义循环相关熵的降噪能力,将广义循环相关熵谱密度与传统基于二阶统计量的谱相关密度进行对比,图9和图10给出了含噪声仿真信号x(t)的谱相关密度图[26],可以看出信号的能量分散在整个双频平面内,谱相关密度的能量聚集性很差,轴承外圈特征频率和系统共振频率已完全被噪声掩盖,难以有效识别。

图9 仿真信号谱相关密度(Contour图)Fig.9 Spectral correlation density of simulative signal (Contour plot)
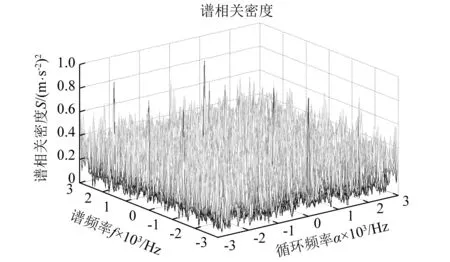
图10 仿真信号谱相关密度(三维图)Fig.10 Spectral correlation density of simulative signal (3D plot)
通过上述仿真信号可以得出以下结论:广义循环相关熵具有很强的从强高斯噪声和非高斯噪声中提取信号特征的能力,基于广义高斯核函数的广义循环相关熵为高斯、非高斯噪声的处理提供了一种崭新的解决方法,其性能优于传统基于二阶统计量的谱相关分析。
4 电机轴承故障诊断
采用美国凯斯西储大学(Case Western Reserve University)轴承数据中心(Bearing Data Center)的网站上公布的试验数据[27]:试验轴承型号为:深沟球轴承6205-2RS JEM SKF,采样频率fs=12 000 Hz,电机负载为空载,电机转速1 797 r/min(fr=29.95 Hz)。两路信号为同一精度的两个传感器对同一目标的不同部位进行测量拾取的振动信号。电机轴承内圈故障振动信号数据记录号为105DE 和125DE,轴承外圈故障振动信号数据记录号为130DE和144DE,构成两路传感器信号,将两路传感器采集的振动信号(以下分别用x和y表示)进行信息融合,计算其广义循环互相关熵谱。计算得到滚动轴承内圈、外圈故障特征频率为[28]
fi=162.185 Hz,fo=107.365 Hz
4.1 轴承内圈故障诊断
图11为滚动轴承内圈故障振动信号x及其FFT。图12为滚动轴承内圈故障振动信号y及其FFT。在图11(a)和图12(a)中存在明显的幅值调制现象,但根据时域波形及其FFT还不能识别轴承故障。
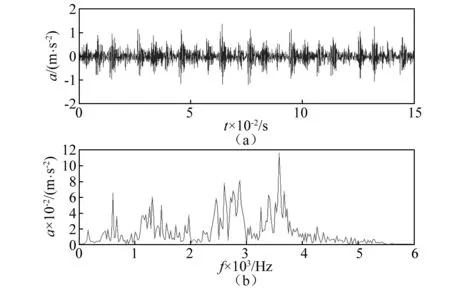
图11 轴承内圈故障振动信号x及其FFTFig.11 Vibration signal x and its FFT with inner race fault
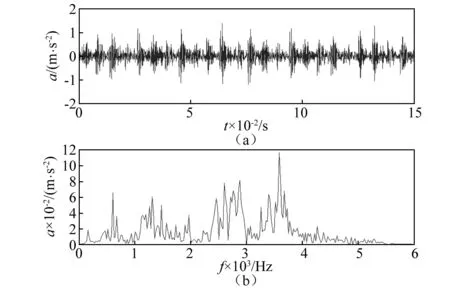
图12 轴承内圈故障振动信号y及其FFTFig.12 Vibration signal y and its FFT with inner race fault
为了验证广义循环互相关熵在轴承故障诊断中的有效性,图13给出了轴承内圈故障振动信号的广义循环互相关熵谱的轮廓图(p=4,σ=1,为清晰显示频谱结构,仅画出了频谱中心部分)。在图13和图14中可以清楚地看到:轴承内圈故障特征fi频率及其倍频,主要沿频谱直线f=±0.5α分布,逐渐由频谱中心向外扩展张成整个频谱平面;以轴承内圈故障特征频率fi的谱峰构成菱形,菱形对角线在水平方向上的长度是2fi,在垂直方向上的长度是fi,这种频谱结构,清晰表达了轴承内圈故障特征频率fi。图14给出了轴承内圈故障振动信号的广义循环互相关熵谱的三维图,从图14中,能更清晰地看到轴承内圈故障特征频率fi的频谱特征及其分布规律。
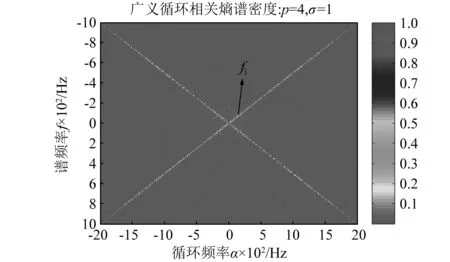
图13 轴承内圈故障振动信号广义循环互相关熵谱Fig.13 Generalized cyclic cross correntropy spectral density of vibration signal with inner race fault (Contour plot)

图14 轴承内圈故障振动信号广义循环互相关熵谱(三维图)Fig.14 Generalized cyclic cross correntropy spectral density of vibration signal with inner race fault (3D plot)
将广义循环互相关熵谱密度与传统基于二阶统计量的谱相关密度进行对比,图15和图16给出了轴承内圈故障振动信号的谱相关密度图,可以看出传统谱相关密度的能量聚集性很差,分辨率较低,不能有效识别轴承内圈故障特征频率fi。
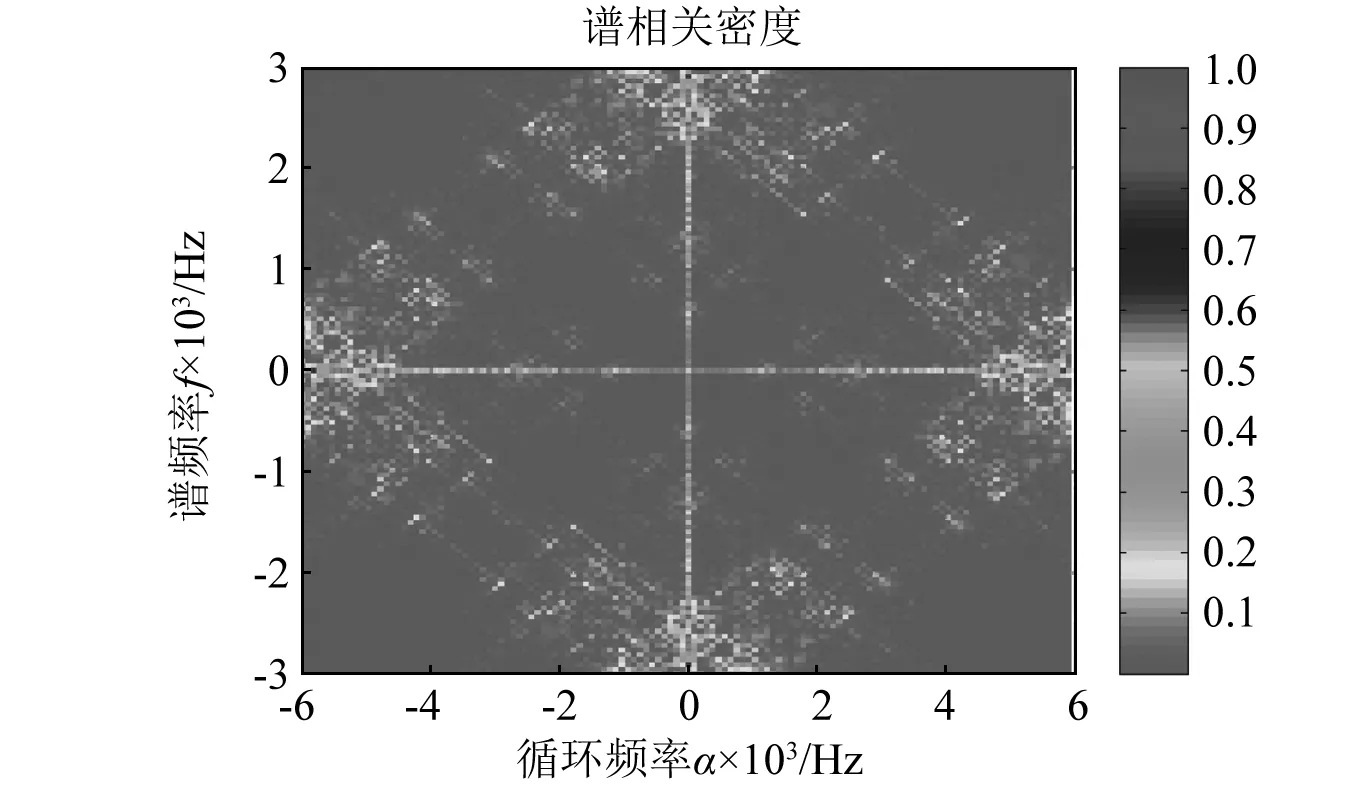
图15 轴承内圈故障振动信号谱相关密度(Contour图)Fig.15 Spectral correlation density of vibration signal with inner race fault (Contour plot)

图16 轴承内圈故障振动信号谱相关密度(三维图)Fig.16 Spectral correlation density of vibration signal with inner race fault (3D plot)
4.2 轴承外圈故障诊断
图17为滚动轴承外圈故障振动信号x及其FFT。图18为滚动轴承外圈故障振动信号y及其FFT。图19为其广义循环互相关熵谱的轮廓图、图20为其广义循环互相关熵谱的三维图(p=4,σ=2)。从图19和图20可以清楚地看到:轴承外圈故障特征频率fo及其倍频,主要沿频谱直线f=±0.5α分布,逐渐由频谱中心向外扩展张成整个频谱平面;轴承外圈故障特征频率fo及其倍频的谱峰构成菱形,菱形对角线在水平方向上的长度是2fo,在垂直方向上的长度是fo,这种频谱结构,清晰表达了轴承外圈故障特征频率fo的分布特征。

图17 轴承外圈故障振动信号x及其FFTFig.17 Vibration signal x and its FFT with outer race fault

图18 轴承外圈故障振动信号y及其FFTFig.18 Vibration signal y and its FFT with outer race fault
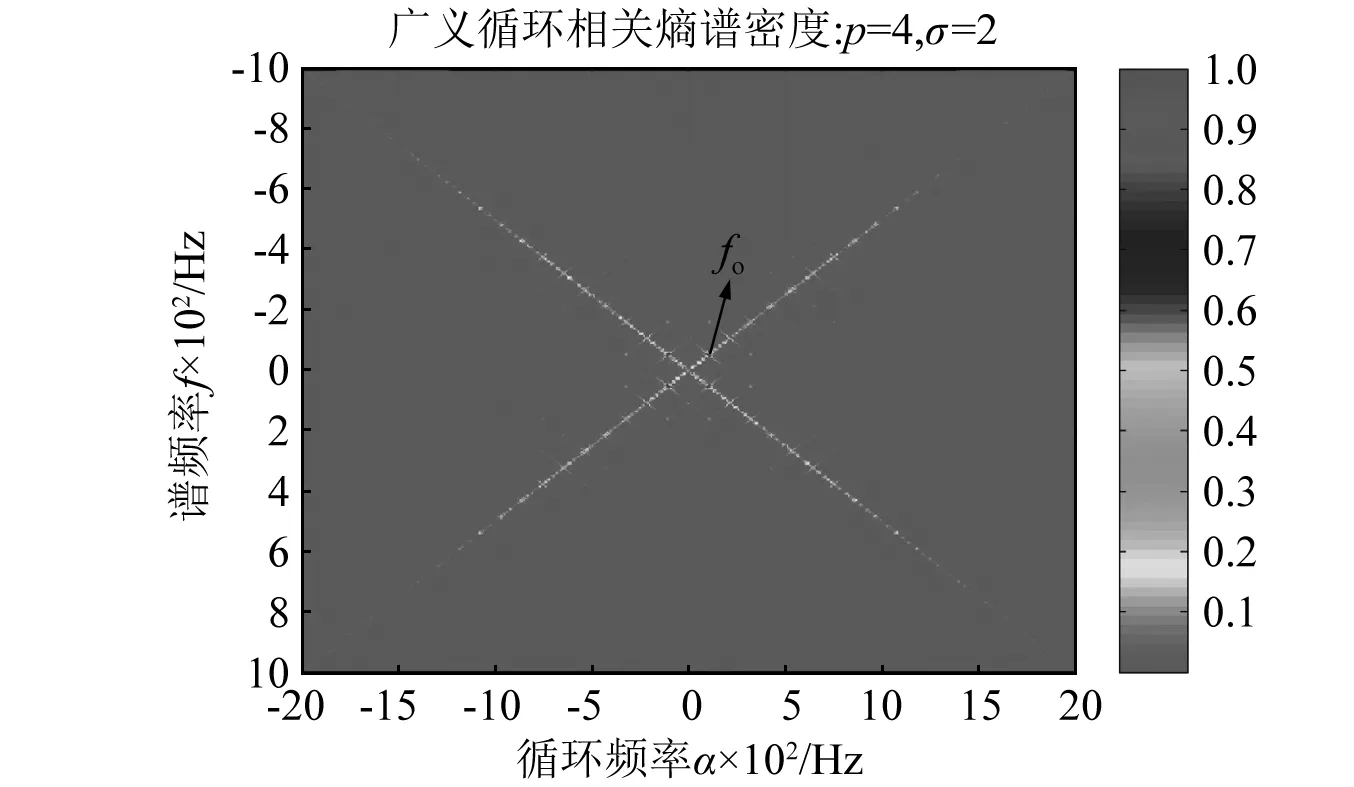
图19 轴承外圈故障振动信号广义循环互相关熵谱Fig.19 Generalized cyclic correntropy spectral density of vibration signal with outer race fault (Contour plot)

图20 轴承外圈故障振动信号广义循环互相关熵谱Fig.20 Generalized cyclic cross correntropy spectral density of vibration signal with outer race fault (3D plot)
图21和图22给出了轴承外圈故障振动信号的谱相关密度图,从图21和图22可以看出传统谱相关密度也不能有效识别轴承外圈故障特征频率。
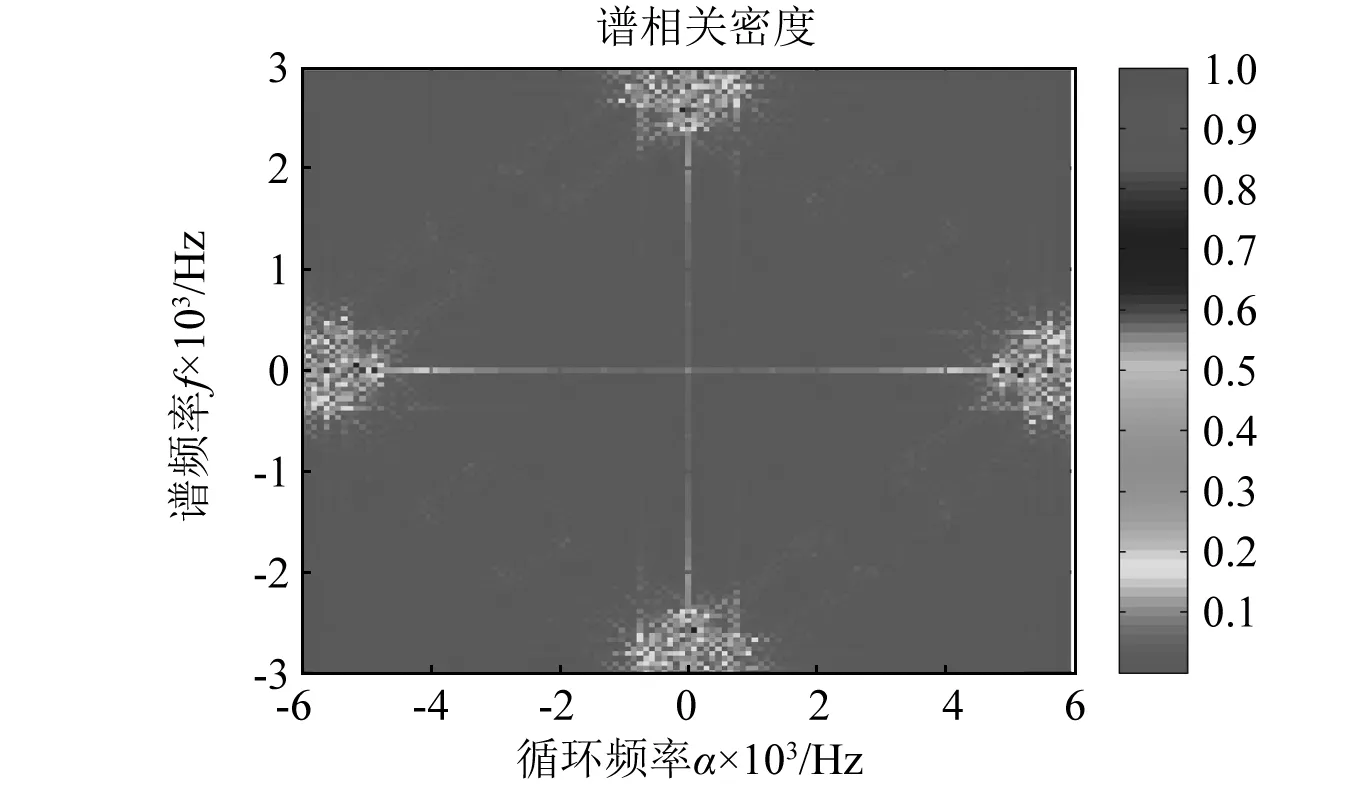
图21 轴承外圈故障振动信号谱相关密度(Contour图)Fig.21 Spectral correlation density of vibration signal with outer race fault (Contour plot)
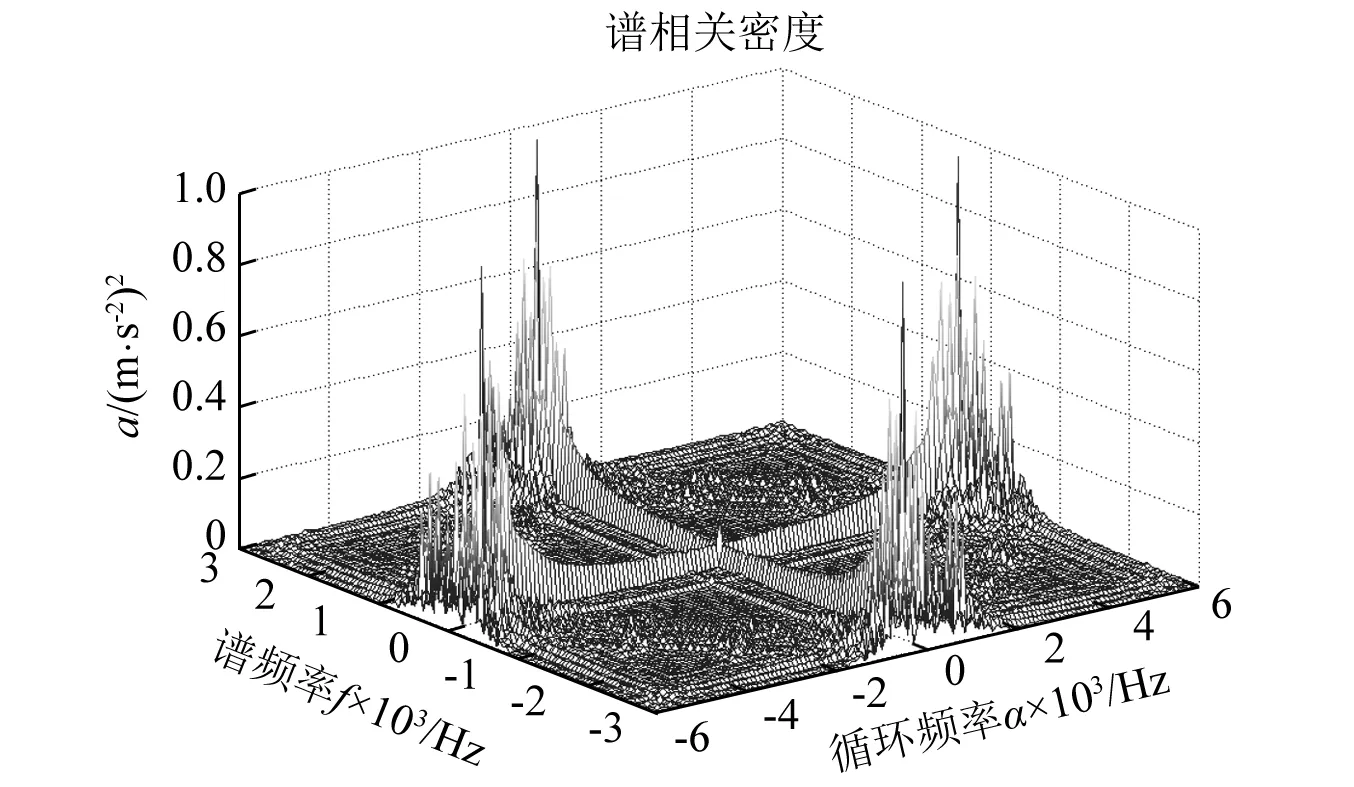
图22 轴承外圈故障振动信号谱相关密度(三维图)Fig.22 Spectral correlation density of vibration signal with outer race fault (3D plot)
通过上述分析可以看出:基于两路传感器振动信号的广义循环互相关熵具有信号解调功能,在由循环频率α和谱频率f构成的双频平面内,能够很清晰地刻画轴承内圈、外圈的故障特征,提高了轴承故障诊断的准确性和可靠性,为从噪声环境中提取轴承故障特征的有效方法,其性能优于传统的基于二阶统计量的谱相关方法。
5 结 论
为提高电机轴承故障诊断的准确性和可靠性,基于循环平稳信号处理、相关熵理论和广义高斯分布,提出了一种基于多传感器信息融合的广义循环互相关熵轴承故障诊断方法。先从广义高斯分布入手,推导了广义相关熵、广义循环互相关熵和广义循环互相关熵谱密度的计算公式;并利用轴承外圈故障仿真信号分析了轴承故障的广义循环互相关熵谱的频谱结构及其特征,并利用该信号对广义循环互相关熵谱的降噪性能进行了验证,表明广义循环互相关熵能够有效处理高斯和非高斯噪声,具有从强噪声环境中提取信号频谱特征的能力。最后将广义循环互相关熵应用于电机滚动轴承内圈、外圈故障诊断,试验结果表明:基于多传感器信息融合的广义循环互相关熵谱能有效提取轴承内圈、外圈故障特征,其性能优于传统基于二阶统计量的谱相关方法。

