一种基于局部回归的多尺度碳市场价格预测模型研究

秦全德， 黄兆荣， 黄凯珊

(1.深圳大学 管理学院,广东 深圳 518060; 2.深圳大学 大湾区国际创新学院,广东 深圳 518060)

0 引言

碳排放权交易是一种控制温室气体排放、推动绿色低碳发展的一种重要市场机制，具有成本有效性和政治可行性[1]。碳排放权交易环境下，碳排放权成为企业的一种新的资产，可以在碳市场中自由买卖。准确可靠的碳市场价格预测是宏观调控碳市场和制定相关的政策，以保证碳市场正常运行的重要支撑基础[2]。

碳市场是一个典型的非线性社会经济复杂系统，与外界具有错综复杂的联系[3]。研究表明碳市场价格序列在本质上是一个高噪声、非线性、非平稳的混沌时间序列[4]。碳市场价格的预测是能源经济与气候变化领域亟待解决的一个关键问题。在已有的文献中大致可以分多元因素模型和时间序列模型。多元因素模型旨在找出与碳市场价格有关的影响因素，通过刻画碳市场价格与影响因素之间的关系，从而实现碳市场价格的预测[5～7]。时间序列预测方法主要包括传统的计量经济学方法和人工智能方法。时间序列预测方法专注于对碳市场价格序列的本身进行建模，不依赖于其他影响因素，通过时间序列来探讨其内在的动力系统特性。凭借便于建模的优点，近年来时间序列预测模型得到学术界广泛关注[8～11]。

捕捉碳市场的多尺度特性有利于处理碳市场价格的不确定性和短期波动性[12]，从而提高碳市场价格预测的性能。基于“分而治之”的思想，多尺度分析首先将复杂的碳市场价格序列分解成多个具有相对结构简单和波动平稳的分量，再分别对分量进行预测，然后对这些分量预测结果进行集成从而得到最终的预测结果[13]。鉴于多尺度方法能够捕捉各个尺度所隐藏的规律与本质特征，近年来，学者们基于经验模态分解(Empirical Mode Decomposition, EMD)的思路提出了一系列适合于非线性、非平稳的经济系统建模的多尺度预测模型。高杨和李健[14]提出了基于EMD和支持向量机的误差修正模型对碳排放核证减排量期货和欧盟碳配额期货价格进行预测。张晨和杨仙子[15]运用极点对称EMD将碳价格时间序列分解为互不耦合的分量，根据不同频率选择各个分量的预测方法，采用支持向量机方法集成预测结果。Zhu等[16]提出了基于集成经验模态分解(Ensemble EMD，EEMD)的多尺度预测模型，该模型运用自回归积分滑动平均模型(ARIMA)和最小二乘支持向量机(LSSVM)分别预测分解后的高频和低频分量。Sun等[17]提出了修正EMD高频分量的二次分解预测框架，并用基于遗传算法优化的BP神经网络预测各个分量。结果表明这些多尺度模型比单一模型具有更好的性能。

EMD方法假定一个复杂的时间序列由许多简单模式的不同尺度组成，其根据序列中的局部极值点使用三次样条插值来平均包络从而分离出不同的模态[18]。作为一种完全局部自适应的方法，EMD可以将非平稳和非线性时间序列的局部特征分解为不同时间尺度的多个波动和趋势项[19]。然而在EMD分解过程中，易出现模式混合现象。EEMD通过引入白噪声克服了模态混叠问题[20]。启发于EMD分解的特点，本文提出一种基于EEMD的碳市场价格预测的多尺度局部回归模型。

在提出的模型中，利用EEMD对原始时间序列进行分解，得到相应的本征模态函数(Intrinsic Mode Function, IMF)和剩余量。利用由Farmer和Sidorowich提出的局部线性预测(Local linear prediction, LLP)方法[21]来预测每个IMF和剩余量。LLP是在非线性动力学框架下应用于混沌时间序列的预测，在处理低维度和平滑问题时表现出良好的预测性能。LLP实施相对简单，不需要长时间序列来训练预测模型，可以用较少的样本进行建模。与人工智能模型相比训练速度快，LLP显著减少了建模时间和难度。迄今，LLP方法和局部多项式预测(Local Polynomial Prediction, LPP)在脑电定量分析诊断[22]、实时语音浊音处理[23]、水文[24]、气温[24]、风速[26]和能源价格[27]等时间序列领域得到较广泛的应用。

本文聚焦分析EEMD框架下LLP的预测能力，进一步探究多种由LLP扩展所得到的正则化局部回归模型，包括对状态向量进行多项式特征处理的LPP、向LLP中引入正则化技术的局部主成分回归、局部偏最小二乘回归和局部岭回归，以及同时具有正则化和自变量选择效果的局部套索回归。在提出的模型中，EEMD-LLP具有简单、有效且易实施的特点，进一步对EEMD-LLP的参数适应性进行分析。

1 多尺度局部回归的预测模型构建

对于具有复杂特性的碳市场价格时间序列，提出一种新颖的基于局部回归的多尺度预测模型。在提出的模型中，根据“先分解后集成”的思想，运用EEMD将原始碳价格序列分解为多个IMF及剩余量，分解后的IMF和剩余量均具有较高的信噪比和较为简单、平稳的模式。基于非线性混沌系统具有自相互作用特征的物理原理，将分解得到的模式通过相空间重构成多变量系统，在拓扑等价的意义下实现当前状态向量与未来状态向量的动力学信息传递[28]。再根据当前状态向量与状态空间中其他向量的距离，进行线性回归(LLP)或多项式回归(LPP)的局部预测。而局部正则化模型模型是分别运用四种正则化思路拟合LLP中当前状态向量的k个最近邻向量xj1,xj2,…,xjk及其对应的未来值，可以得到局部岭回归预测(LRR)模型、局部主成分回归(LPCR)、局部偏最小二乘回归(LPLSR)和局部套索回归(LLASSO)。综上，提出的多尺度局部回归碳市场价格预测模型具体过程描述如下：

(1)将原始的非线性、非平稳的碳市场价格时间序列用EEMD方法分解成n个IMF和一个剩余量。

(2)对提取到的各IMF和剩余量采用超参数搜索方法通过选择该适用于该分量的嵌入维数m和延迟时间τ，然后使用确定参数后的局部回归模型对相应分量进行建模及预测。

(3)加和集成被证明是一种简单有效的方法[29,30]。因此，将所有IMF和剩余量的预测结果相加，得到最终预测结果。

2 实验研究

2.1 数据与模型设置

为了验证所提出的模型框架的有效性，使用欧洲气候交易所(ECX)中欧盟排放配额(EUA)期货价格作为研究数据。由于EUA期货的交易量最大，对EUA期货价格的预测可以较好反映碳交易市场的总体态势。表1中阐述了Dec14和Dec15各个子集范围，交易日期范围中不包括公共节假日。

表1 碳期货价格样本范围

参考EEMD的常用参数设定，白噪声数量和标准差分别设置为100和0.2[16]。本文采用斜率匹配波形延拓法处理端点效应[31]。提出模型涉及的参数包括嵌入维m，延迟时间t，最近邻数量k，以及正则化模型需要设定的参数包括主成分回归和偏最小二乘回归中的主成分个数v，岭回归、套索回归中的约束参数b。采用超参数搜索方法确定每个分量的最优参数，其中m、t、v和b由格搜索确定，k采用随机搜索[32]。将实验数据分为三个子集：训练集，验证集和测试集，其中训练集占序列长度的70%，验证集合测试集皆占15%。为了验证提出模型的有效性，选取基于EEMD的支持向量回归(SVR)和人工神经网络(ANN)作为基准模型。对于SVR的核函数选择，选择常用的高斯核函数，通过格搜索方法设置参数S2和g；ANN模型的隐藏节点设置为7，输入神经元由验证集决定[10]。

2.2 实验结果

在使用的建模方法中，EEMD分解使用Matlab 2012b软件进行程序编写，局部回归预测模型皆采用Python 2.7的Scikit-Learn程序库[33]。为了验证所提出的基于EEMD分解的局部回归模型的预测能力，使用均方根误差(RMSE)和方向统计量Dstat对模型的水平预测和方向预测的性能进行评估。各模型预测的RMSE和Dstat值分别见表2和表3。DM检验和RT检验的结果如表4和表5所示。

根据RMSE的结果，EEMD-LLP在对Dec14和Dec15的碳市场价格预测中均优于其它模型。相比于基准模型EEMD-SVR和EEMD-ANN，除表现不稳定的EEMD-LLASSO模型外，其余的五种局部回归模型的效果皆好于基准模型。相较于SVR、ANN这类全局非线性模型，局部线性回归模型在EEMD框架下更能模拟具有相对简单、平稳特征的IMF和剩余量的动态演变。对于方向指标Dstat，除EEMD-LLASSO外提出的局部回归模型的预测效果皆好于基准模型，其中EEMD-LLP和EEMD-LPP的性能更为突出。

在表4的DM检验和表5的RT检验中，目标模型排列顺序根据表2和表3的预测指标RMSE和Dstat的排名确定，预测性能较弱的模型排列在前。在表4中，DM检验值为负表明目标模型的水平预测能力强于基准模型；反之，弱于基准模型[34]。对于RT检验，RT检验值的正负所代表的含义与DM检验相反。表4和表5中括号数值内表示显著性水平。在对Dec14的水平预测中，DM检验结果表明EEMD-LLP在5%的显著性水平上优于EEMD-LPCR，EEMD-LPLSR，EEMD-SVR和EEMD-ANN。对于Dec15序列，EEMD-LLP在5%的显著性水平上优于EEMD-LPP，EEMD-LASSO、EEMD-SVR和EEMD-ANN。对于Dec14的方向预测，RT检验结果表明提出的局部回归模型的准确性皆在5%的显著性水平上优于EEMD-ANN。在Dec15的方向预测中，除EEMD-LASSO外，提出的其他局部回归模型的方向准确性皆在5%的显著性水平上优于EEMD-ANN。

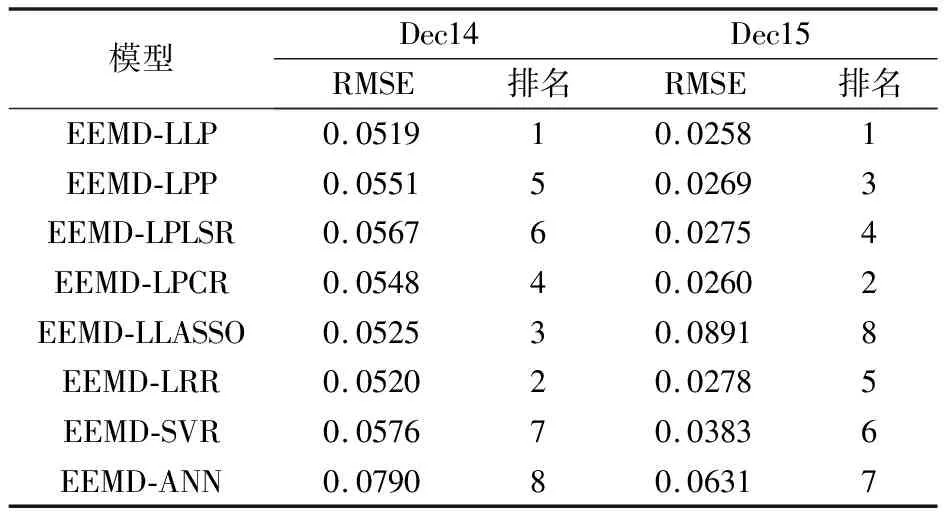
表2 模型预测的DstatRMSE值比较

表3 模型预测的Dstat值比较

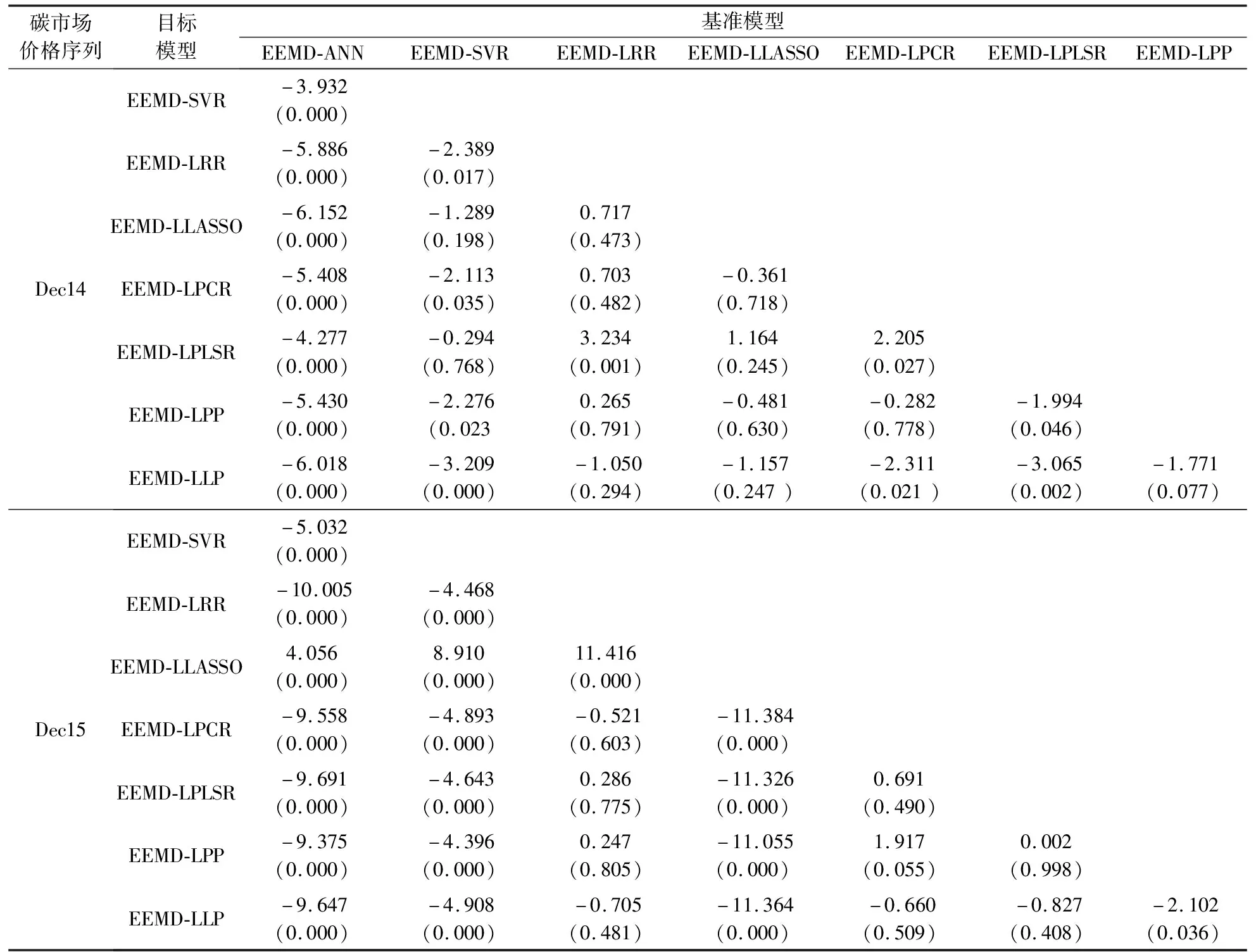
表4 DM检验的结果

表5 RT检验的结果

在Dec14和Dec15上，EEMD-LLP和EEMD-LPP的方向准确性皆在5%的显著性水平上优于EEMD-SVR。EEMD-LLP仅在DEC14数据集的预测方向精度略次于EEMD-LPP，但二者的差异并不显著。在对Dec14的水平预测中，DM检验结果表明EEMD-LLP在5%的显著性水平上优于EEMD-LPCR，EEMD-LPLSR，EEMD-SVR和EEMD-ANN。对于Dec15的水平预测，EEMD-LLP在5%的显著性水平上优于EEMD-LPP，EEMD-LASSO、EEMD-SVR和EEMD-ANN。因此，可以发现在碳期货价格时间序列预测上，LLP模型相对于其他基于正则化和成分提取的扩展的局部回归模型在EEMD框架下泛化能力更强，在水平预测和方向预测都表现出了较好的预测效果。此外，相对于其他局部回归模型，LLP需要人工调节的参数较少，降低了建模难度和计算时间。

2.3 结果讨论

由以上实验结果可以发现，除了EEMD-LLASSO外，提出的其他局部回归模型皆优于基准模型，表明相较于SVR、ANN这类全局非线性模型，局部回归模型在EEMD框架下对碳市场价格预测具有更好的性能。

EEMD-LLP在RMSE和的综合预测性能，说明了EEMD-LLP具有优秀的碳市场价格预测能力和稳定性，表明LLP相对更适合于EEMD框架下各分量的预测。本文发现其他局部回归预测方法中，EEMD-LPP，EEMD-LPCR，EEMD-PLSR，EEMD-LRR模型的差异较小。相较于原始的LLP方法，其他局部回归策略虽然提高了拟合测试集复杂非线性的能力，但增加了陷入过拟合的可能性。对于LPSLR和LPCR算法中提取主成分操作具有一定的去噪效果，但也使其预测某些分量时丢失自变量的部分信息。带有绝对值正则项的EEMD-LLASSO模型不稳定，原因在于绝对值正则项的引入使得模型具有自变量子集选择的效果，在回归拟合中使得某些模型认为不重要的自变量的系数为0，其丢失信息的可能性则比EEMD-LPCR，EEMD-PLSR要大。LPP算法引入了二次项和LRR算法引入的平方正则项，相当于对预测模型添加更多的先验知识，但对参数引入先验分布也可能增加了模型的误差，在寻找最优参数时，趋向于选择小的正则化参数。另外，可能在只考虑收盘价格的情况下不存在多因素信息冗余，采用降维和正则化策略容易丢失信息，降低了模型的泛化能力。

在时间序列预测中，相空间重构后状态向量各嵌入维皆含有对模型预测有用的信息。一旦在使用训练集和验证集进行正则项参数的选择时出现了一定程度的过拟合从而在使得某些嵌入维变量的系数为0，模型的预测效果将会受到较大的影响。除了EEMD-LLASSO外，提出的其他局部回归模型皆优于基准模型。相较于SVR、ANN这类全局非线性模型，局部回归模型在EEMD框架下具有更好的预测能力。

2.4 参数适应性分析

提出的基于局部回归的多尺度预测模型包含多个需要人工指定的参数，如嵌入维m，延迟时间τ以及最近邻数量k等，在对每个IMF及剩余量建模时需要对这些参数进行搜索确定，较大增加了建模难度和计算时间。鉴于EEMD-LLP简单、有效和易用性，对EEMD-LLP参数的适应性进行分析，试图确定适用于所有IMF及剩余量的参数组合。

为研究EEMD-LLP参数的影响，以Dec15为例，所有分解后的分量都采用相同参数的LLP进行预测。为便于和前述实验做比较，使用与之前实验相同的测试集划分。将总训练集的长度记为N。图2展示了固定最近邻参数k，嵌入维m和延迟时间τ的改变对RMSE和Dstat的影响，其中m和τ的设置与前述实验一致，k固定为前述实验中通过随机搜索寻找到的所有分量的最近邻参数的平均值。由图3可看出延迟时间τ的选择对模型的预测能力影响较大，当τ=1时，EEMD-LLP在RMSE和Dstat上的表现都远好于其他值，且随着τ的增大，模型的RMSE越来越大。当τ∈[2,4]时，模型在Dstat指标上的性能受到嵌入维的影响因而最优值差异不大。由此可知，若将EEMD分解的所有分量都使用同一参数τ，则τ=1为最优的选择。在τ为最优值的情况下，m∈[3,5]时LLP在RMSE和Dstat上皆取得较好的结果，差异较小。随着m的增大，RMSE以比较缓的趋势逐渐增大，Dstat亦有下降的趋势，可以得出m∈[3,5]为所有分量设置相同的嵌入维时最佳的参数范围。图3展示了将延迟时间τ固定为1，嵌入维m的范围设置为[3,6],最近邻参数k的范围从总训练集长度N的10%到100%变化对EEMD-LLP模型性能的影响。从RMSE的结果可以发现在m不同的嵌入维参数下，k的最优值出现在0.2N到0.7N之间。由此可以看出，相比于全局建模，局部建模能够带来预测效果的提升。在各个嵌入维参数的实验结果中，当k=0.1N时，RMSE结果相比于其他参数性能较差，表明了当使用局部回归模型时，若最近邻状态空间向量的数量太少时，模型无法获得足够多的信息，从而降低了模型的预测能力。可以发现Dstat的波动对k的取值不敏感，说明k的取值主要影响模型在水平预测上的效果。

从RMSE和Dstat的数值可知，当所有分量使用同一个参数的EEMD-LLP的预测效果与前面实验中通过验证集搜索最优参数的效果相近。这是在于验证集搜索最优参数可能造成了一定的过拟合。各分量皆使用同一组参数使得整个EEMD-LLP框架的更为简单，提高了整体模型的泛化能力。根据上面的实验结果及分析，可以得出EEMD-LLP的一组最优参数：m=5，τ=1和k=0.5N。

在EEMD-LLP模型中，最佳参数延迟时间τ=1，嵌入维度m=5，预测的滑动窗口仅考虑预测点的前5天可以达到最高的预测精度，这预示着碳期货价格可能受到周线的影响较大。从LLP的参数k中可以观察到国际碳期货市场的局部周期尺度属性。当最近邻数量取得362.5天(k=0.5N)左右时，是局部回归算法所确定的较佳训练集长度。由于波动的厚尾分布和长程相关性，碳市场价格序列存在多重分形特征，尺度行为特征会随时间变化[35]。如果进行全局建模，难以有效地刻画具有碳期货价格时、频两域的局部特征。通过LLP方法中参数k的调整，可以较好把握多分形序列多样的局部尺度特性。

2.5 新近研究比较

进一步研究和证明所提出的EEMD-LLP的预测能力，将EEMD-LLP与Zhu等[16]提出的一种自适应多尺度集成学习范式进行了比较。为比较公平，选择了与原始文献中相同的观测样本、训练集及测试集，其中LLP的参数设置使用了上文实验中提出的最优参数组合。实验对比结果如中表6所示，其他模型的结果直接来源于原始文献。从表6可知，无论是水平预测还是方向预测，EEMD-LLP都优于EEMD-LSSVM, EEMD-ARIMA, LSSVM和ARIMA方法。将EEMD-LLP与文献[16]提出的EEMD-HLT-Σ模型相比，水平预测的效果优于该模型，但在方向预测上稍差。表明EEMD-LLP在碳市场价格时间序列上的具有优越的水平预测和方向预测能力。可以看出EEMD-LLP具有简单易实施和预测性能优异的特点，是一种具有潜力的碳市场价格预测方法。

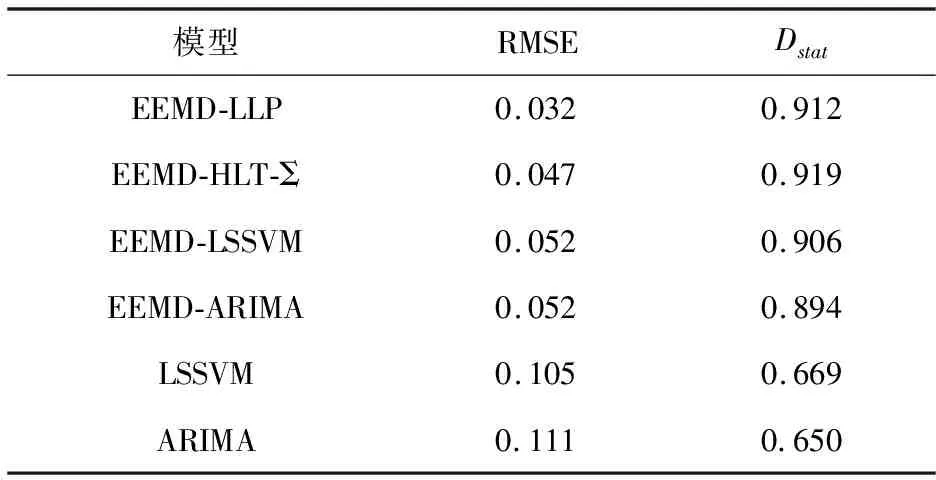
表6 与新近研究模型的比较

3 结论

为了提高碳市场价格时间序列的预测精度，基于“分而治之”的思想，本文提出了基于局部回归的多尺度碳市场价格预测模型。构建的模型采用EEMD将原非线性、非平稳的碳市场价格时间序列自适应分解成多个具有简单模式的IMF和剩余量。根据EEMD局部特征分解的特点，运用局部回归模型对各个分量进行预测，然后将各分量预测的结果加总集成作为最终的预测结果。选择了欧洲气候交易所的两个碳市场期货价格作为研究对象，研究结果表明提出的基于局部回归的多尺度模型在水平预测和方向预测都具有较好的性能。研究表明在多尺度框架下，运用局部回归方法能够有效提升碳市场价格预测的性能。在提出的模型中所有的分量都使用同一种局部回归的预测方法，这对于每个分量的预测而言可能并非最优的选择。