煤炭码头船货匹配下泊位动态分配多目标优化模型及算法

邰世文， 商剑平， 饶卫振

(1.中交水运规划设计院有限公司,北京 100007; 2.山东科技大学 经济管理学院,山东 青岛 266590)

0 引言

我国煤炭运输形成了“北煤南运”、“西煤东运”的基本格局[1]，输出型煤炭码头是我国煤运输体系的关键枢纽。输出型煤炭码头的运营模式是：列车运输煤炭到港口，翻堆作业系统卸车并将煤炭堆存到堆场；船舶靠泊后，取装作业系统从堆场取煤并传送到泊位装船，装船完成后离港。输出型煤炭码头输入(卸车)的目的是输出(装船)，泊位分配是码头煤炭输出调度计划的起点，其重要性不言而喻。输出型煤炭码头泊位分配问题不仅仅是单纯考虑泊位规格和装船设备下的船舶匹配泊位，还应考虑船舶票货及装船方案、煤种在堆场中的垛位分布及堆存量、取装作业系统、装船作业过程以及靠离泊规则等，即船货匹配下的泊位分配问题。较优的泊位分配，可以最大限度的避免泊位资源浪费，提高堆场煤源的利用情况，减少设备冲突，缩短船舶在港时间。

当前，关于码头泊位分配问题研究越来越多的与船舶靠泊后的实际生产挂钩，并考虑其关联的影响因素，如泊位分配与岸桥调度相互影响方面的研究[2～5]，泊位分配与堆场相互影响的研究[6,7]，泊位分配与燃油消耗相互影响的研究[8]。大规模泊位分配问题求解方面，流行的算法主要有遗传算法[2,4,9,10]、粒子群算法[11]、模拟退火算法[12]等。煤炭码头卸车调度方面，刘文远等[13]着重研究了煤炭码头列车等待和作业总时间最短的列车-翻车机-堆场联合调度优化问题；邰世文[14]研究了煤炭码头考虑列车-翻堆线-堆场的卸车生产调度问题多约束多目标优化模型及其遗传算法。目前关于煤炭码头泊位分配问题的研究文献非常有限：有Robenek等[15]从战术层面上研究了散货港口的泊位分配和堆场分配问题，但其前提假设是所有船舶都是单一货种，优化目标单一；宓为建等[16]针对出口型煤码头泊位分配问题，以岸线、机械利用率最大和船舶总在港时间最短为目标建立泊位与机械联合调度模型并用遗传算法求解，但仅区分块煤和末煤，而且未考虑场存、工艺可达等边界条件，船舶在泊时间估算粗略。实际应用层面，国内煤炭码头泊位分配严重依赖于人脑经验，由于影响因素众多，工作人员很难站在全局角度分配泊位。

综上，输出型煤炭码头泊位分配问题不仅仅是单纯的船舶匹配泊位，然而当前大多研究仅单一考虑堆场或设备因素且过于理想化，实用性较低。因此，本文针对输出型煤炭码头船货匹配下的泊位分配问题，考虑船舶票货及装船方案、煤种在堆场中的垛位分布及堆存量、垛位与取料机的可达性、取装线、装船机与泊位的可达性、泊位规格限制、航道开放时间和装船作业规则等边界条件，建立了多约束多目标数学模型，并设计了采用仿真推演策略解码的遗传算法求解。本研究旨在为解决具有船货匹配、动态调度、多约束、多目标等特点的复杂、大型输出型煤炭码头泊位分配问题提供新的解决途径。

1 问题的描述

船舶在码头接受服务的整个过程是：船舶抵锚→在航道开放进港时间进港靠泊→第一轮装船作业并同时排压舱水→第二轮装船作业→第三轮装船作业(调水尺)→在航道开放出港时间离泊，装船作业过程需要按照船方配载步骤依次进行取装作业。煤炭流经取装线的关键节点是：堆垛→取料机(或给料机)及其相连的皮带→转接皮带→装船机→船舱，取装线设备节点会存在交叉的情况。一般来说，船舶装船需求可能是多票货，每票货可以是多个装船方案，每个装船方案可以是单个煤种(如神混1单装)或者两个煤种按一定比例配煤(如神混1:神优1=2:1)，多条船舶可能存在共用一个装船方案或装船煤种情况。

输出型煤炭码头典型布局如图1所示，整个堆场由露天堆场和封闭筒仓构成(取料机移动到相应垛位取料，给料机固定在筒仓底端供料)，受取装线限制，不同的堆场可达不同的泊位，如筒仓排A和B均可达泊位201和202。

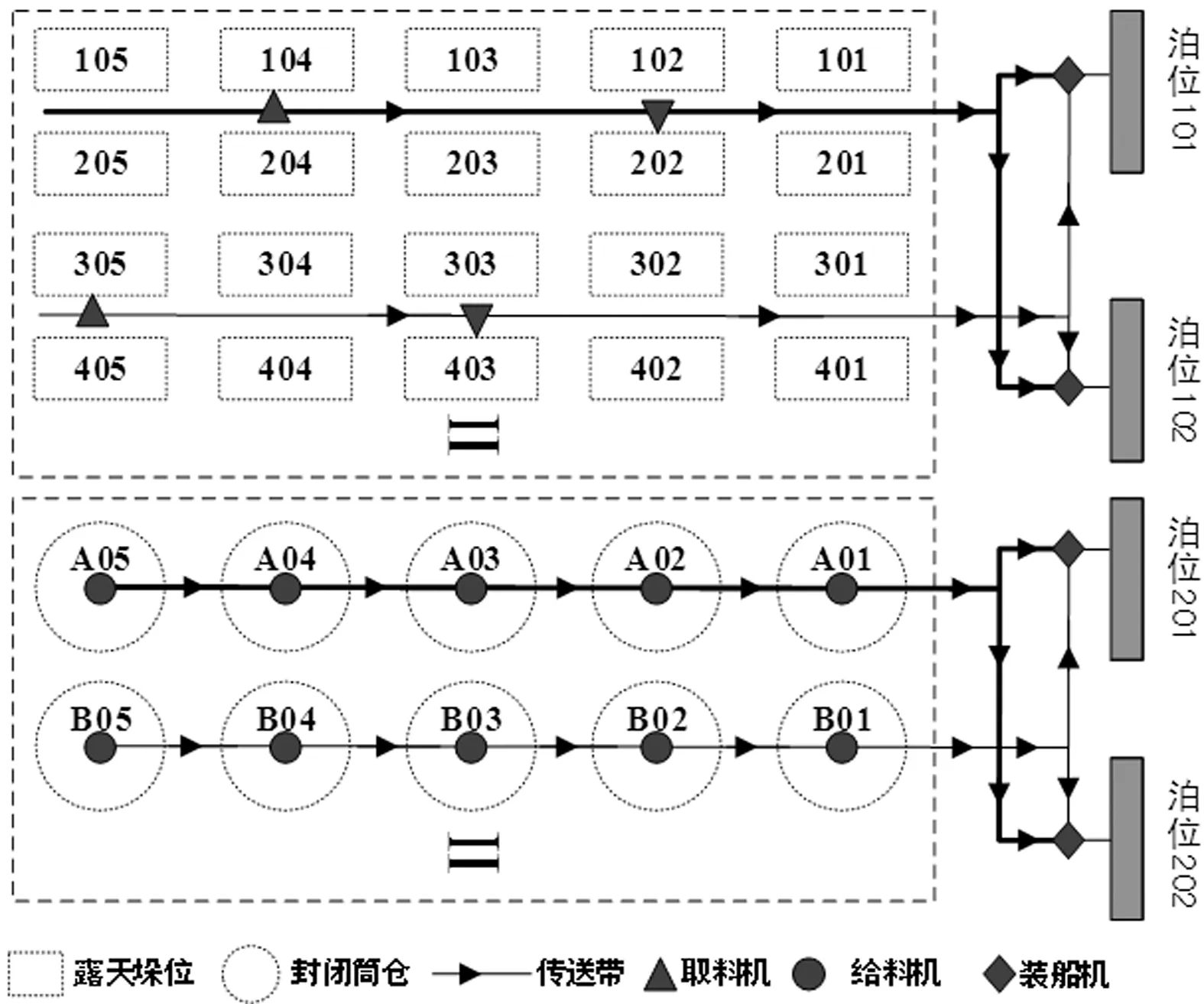
图1 输出型煤炭码头典型布局

本研究问题可以描述为：有s个不同的垛位(垛位位置、类型、堆存煤种等不同)、e条取料线(包括取料机或给料机及其相连的传送皮带，取料线与垛位的可达性关系为一对多)、l台装船机(受取装工艺限制，取料线与装船机的可达性关系为多对多)、m个不同规格的泊位(装船机与泊位的可达性关系为多对多)；有n条抵锚或预到船舶，每条船舶可以配载1～3票货(票货量固定)，每票货对应装船方案为1～3个，每个装船方案可以是一个堆存煤种单装或由两个堆存煤种按一定比例配煤(同一取装线上的垛位才能配煤)；按照船舶具备排船条件的时间顺序，将n条船分配到m个泊位上，并给出装船方案计划装载量、垛位和船舶的计划靠离泊时间，使得码头作业效率最大和船舶在港时间最短。

为便于建模及求解，在符合其实用性的前提下，本文设定以下前提条件：

①待排船舶包括抵锚和预到船舶(动态调度)，船舶具备排船条件时间滚动变化。

②一条船舶只能停靠一个泊位，不考虑移泊。

③航道开放进港、离港时间点固定，船舶从锚地到泊位以及从泊位离港的时长固定。

④船舶装船作业分三轮，靠泊后开始排水和第一轮作业，排水和第一轮作业均完成后方可进行第二轮作业，第一、二轮作业效率取历史平均值，第三轮(调水尺)作业时长取历史平均值。

⑤转接皮带充足，一条取装线由取料线(取料机或给料机及其相连的传送皮带)和装船机唯一确定。

⑥取装线一次装船作业准备时长取平均值。

⑦泊位、垛位及取装设备等抽象为中心点。

⑧煤源充足，忽略设备故障、天气等情况导致的延迟。

本文使用的符号说明如表1所示。

表1 符号说明表

2 模型的构建

2.1 目标函数

本文问题模型的目标函数为港口生产效率最大和船舶在港时间最短，表示如下:

(1)

(2)

(3)

(4)

(5)

(6)

2.2 约束条件

本模型的约束条件主要包括泊位规格限制、作业唯一性约束、进出港时间限制、装船煤种场存充足及取值范围限制等约束条件，表示如下:

(7)

(8)

(9)

(10)

(11)

(12)

(13)

∀j∈B,∀i∈V,∀i′∈V,i≠i′,xij=1,xi′j=1

(14)

(15)

(16)

(17)

(18)

(19)

3 遗传算法设计

泊位分配问题是已经被证明了的NP-Hard问题，遗传算法是应用最广泛的智能求解算法之一[2,4,9,10,16]，而仿真能够用一个虚拟的系统描述真实系统的运行、演变及其发展过程[14,17]。为更好地接近煤炭码头船舶系统运行情况，提高结果精确性，本文将遗传算法与仿真推演结合求解本研究问题。

3.1 编码设计

编码的目的是将问题的可行解从其解空间转换为求解算法的搜索空间中，其设计质量对求解效果有较大影响。基于本问题模型的特点，本文提出了一种组合式编码方法，介绍如下：

(1)编码

在本研究问题中，编码需要描述的解空间包括船舶停靠的泊位、在泊位上的作业顺序、采用的装船方案垛位及装船量、接受服务的时间点。其中，一条船舶仅且仅能对应一个泊位，船舶在泊位上的服务顺序按照船舶具备排船条件时间排序，采用的装船方案可以通过设定装船方案优先级的方式来解决，实际采用的装船方案的垛位、装船量和作业时间可以根据船舶作业时选择启用的取装线、票货量、垛位实时堆存量以及作业效率等计算得到。为了减少编码长度，缩小解空间的规模，本文染色体编码仅考虑船舶作业泊位和装船方案优先级，而装船方案垛位、装船量和作业时间在仿真推演装船作业过程中计算。因此，本文设计的染色体由泊位序列和装船方案优先级序列构成，如图2所示。

图2 染色体编码示意图

①泊位序列Berth={b1,b2,…,bn-1,bn}。如bi=j，表示第i条船作业的泊位为j。

于是，本模型的任意一种方案可由(Berth，Order)唯一表示。所有船舶根据Berth序列分配到相应泊位上，根据船舶具备排船条件时间确定船舶在泊位上的靠泊顺序；然后根据Order序列确定方案的优先级，综合航道开放时间、装船工艺可达性、场存量、票货量、船舶轮次配载量、作业效率以及装船作业启发式优化规则等进行仿真推演计算，可以得到装船方案仿真装载量、取料垛位、装船作业时间和船舶的计划靠离泊时间。

(2)初始种群生成

由于船舶可分配的泊位除了需要满足船舶与泊位的吨级、长度、宽度和吃水深度匹配情况外，还应考虑装船方案煤种的堆存位置与泊位的可达性以及堆存量与配载量关系等约束。因此，在生成染色体时需要确保染色体的合法性，本文设计的染色体生成规则如下：

①从船舶队列取出i船，根据公式(7)～(10)初步筛选符合限制的可用泊位集合Bi；

②根据公式(15)(19)计算货源情况，删除掉集合Bi中不满足约束的泊位；

③从集合Bi中随机选择一个泊位赋值基因位bi，生成Berth序列；

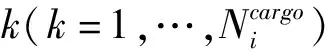
⑤返回到①生成下一染色体。

3.2 仿真推演解码设计

由于本问题牵扯到的变量较多、船舶作业过程顺序严格、作业工艺约束较多，仅仅通过简单的编码和解码较难反应作业的真实情况。这就需要染色体解码时，利用仿真技术来推演各调度方案的运行情况，并统计分析相应的目标函数值作为各染色体的适应值，最终求得较优的解。首先，介绍仿真推演过程中船舶作业各个节点的开始和结束时间的计算方法，如下：

令i′和i船是先后靠j泊位作业的两条船，i′船离开j泊位后，i船在第w个进港时间点到j泊位作业，则i船的进港靠泊各时间节点及泊位状态如下:

(20)

(21)

(22)

(23)

(24)

其中，式(20)表示i船的进港靠泊开始时间为第w个进港时间点，该时间点要晚于i船到港时间和i′船的离泊时间；式(21)表示j泊位从i船开始进港靠泊的时刻起就为被占用状态；式(22)表示i船的靠泊完成时间，该时间也是船舶开始排水时间，见式(23)，若i船靠泊完成后即装船作业，则该时间也是船舶开始作业时间(第一轮装船作业开始时间)；式(24)表示船舶排水完成时间。

令在t0时刻a取料线及相连的z装船机开始空闲，在t1时刻i船舶具备进行第g轮装船作业，且i船舶能使用该取装线从u垛位取料进行装船作业，则应满足如下约束条件:

(25)

(26)

(27)

(28)

(29)

(30)

同时，在作业期间取装线被占用，表示如下:

(31)

其次，令第一轮完成作业时间为t4，则i船舶具备第二轮开始作业的条件的时间t5为:

(32)

重复公式(25)～(32)过程可以计算i船舶第一、二轮装船作业开始和结束过程中的装船垛位、取装量及时间节点。令第三轮装船作业开始时间为t6，则第三轮装船作业完成时间t7和船舶作业完成时间表示如下:

(33)

(34)

最后，完成装船作业后船舶在航道开放船舶出港的第w个时间点离泊出港，离港时间为:

(35)

本文采用事件调度法进行仿真推演解码，详细步骤如下：

①初始化仿真时钟以及泊位、设备、堆场和取装线(取料线和装船机)状态。

②处理船舶：将未到港船舶的到港事件加入事件列表；将已抵锚未靠泊船舶放入到等待靠泊列表；对于正在装船作业船舶，根据装船进度(第几轮作业、装船作业记录、已完成票货量、正在装船作业的取装线和垛位信息)计算流本次装船作业量及完成时间，将一次装船作业完成事件加入事件列表；对于在泊等待作业的船舶，加入等待作业列表。

③推进仿真时钟，处理事件列表直到空为止：船舶到港事件发生时，将船舶加入到等待靠泊列表；船舶具备靠泊条件或泊位空闲事件发生时执行④；船舶具备作业条件或一次装船作业完成时执行⑤。

④针对空闲的泊位，从等待靠泊列表取出i船，若bi与该泊位相同，则根据船舶配载量、装船方案、场存情况，按照公式(15)(19)计算船货匹配情况，选择第一艘船货匹配的船舶，根据公式(20)～(24)更新船舶进港靠泊各时间节点及状态。

⑤针对空闲的取装流程，根据在泊船舶靠泊顺序及装船方案优先级模拟装船作业，根据公式(25)～(35)计算船舶的作业时间和垛位剩余堆存量、并更新船舶状态和设备状态，若完成作业则计算船舶离泊时间，将一次装船作业完成事件或泊位空闲事件加入事件列表。

3.3 适应值函数设计

本算法适应值函数的设计是在式(4)的基础上作如下变换:

(36)

3.4 遗传操作设计

遗传算法针对由多个可行染色体构成的种群，通过选择、交叉和变异进行迭代寻优。目前，常用的选择方法有轮盘赌法、随机遍历抽样法、局部选择和锦标赛选择等，常用的交叉方法有单点交叉、多点交叉、算术交叉、顺序交叉、部分映射交叉和循环交叉等，常用的变异方法有实值变异、替换变异、互换式变异等。基于前述编码方式，本算法的遗传操作设计如下：

①选择操作：采用最流行的轮盘赌法和保优策略结合的方法。选择时，首先采用轮盘赌法，从父代中选出一定比例的染色体，以进行后续的交叉和变异操作产生子代个体；然后采取保优策略，从子代个体和父代个体中选择适应值、目标1和目标2较大的个体进入下一轮的遗传操作，使进化过程中的优秀个体全部保留下来。

②交叉操作：交叉操作是遗传造作中最重要的一环，本文为了增加交叉的多样性，设计了三种交叉策略，以不同的概率进行相应的交叉操作。第一种是以船舶为单位同时分别两点交叉染色体的两个序列；第二种是保持Berth序列不变，对Order序列内每条船以票货为单位进行单点交叉；第三种是Berth序列保持不变，对Order序列内的每条船舶的每票货的基因片段进行部分映射交叉。

③变异操作：变异操作包括两种，染色体变异时，以一定的概率选择一种或两种策略进行相应的变异操作。第一种是仅对Berth序列的交换变异，合法范围内随机选取2个基因位交换泊位；第二种是对Order序列变异，随机选取一条船内的任一票货，随机交换该票货内装船方案的顺序。

4 研究应用情况

4.1 实例概况

本文算法用JAVA编程实现，开发了黄骅港煤炭码头泊位计划智能排产系统，以黄骅港煤炭码头实际数据为例验证模型及算法的有效性。黄骅港煤炭码头是国内煤炭出口大港，有17个煤炭泊位，3个露天堆场共计122个垛位，1个筒仓堆场共计48个筒仓，堆存煤种38个，取料线14条，装船机13台，取装线46条，2018年煤炭量下水量超过2亿吨。

4.2 算例分析

本文取黄骅港煤炭码头某一时点的实际数据(在泊船舶14条，正在进港船舶2条，锚地船舶29条，预到船舶1条)，在配置为CPU Intel 4核1.6GHz、内存8G的计算机上测试。

经统计，程序计算时长约257.39秒。适应值函数及目标函数收敛曲线如图3所示，可以看出算法从约84代开始收敛，算法收敛性和执行效率较高。

图3 适应值函数及目标函数收敛曲线

泊位分配结果如图4所示，30条待排船舶的总在港时间3775小时(单船平均在港5.2天)，计划开始时间2019-01-07 13:00:00，船舶最晚离泊时间2019-01-10 10:00:00，计划时长69小时。图4主界面X轴为时间轴，Y轴为泊位号，2019-01-07 13:00:00处的竖线为计划开始时间截线，与其相交的有14条在泊船舶和2条正在进港船舶，图中一个图形代表一条船，图形内数据分别表示船号、船名、配载吨和装船进度，如泊位100后的第二个图形表示：船舶号为19858，船名为长旺门，配载为17300吨，计划在船舶中汇22离泊后靠泊，计划靠泊时间是2019-01-07 20:00:00，计划离泊时间是2019-01-08 14:00:00。

图4 程序计算的泊位分配方案

有经验的计划人员一次制定本实例30条船舶的泊位方案平均约耗时120分钟，本文用计算机模拟人工方案的结果如图5所示，30条待排船舶总在港时间4207小时(单船平均在港5.8天)，计划开始时间2019-01-07 13:00:00，船舶最晚离泊时间2019-01-10 14:00:00，计划时长73小时。

图5 计划人员制定的泊位分配方案

通过对比可知，人工制定的泊位分配方案在耗费工时、船舶总在港时间和计划时长方面分别是系统计算结果的28倍、1.1倍和1.1倍。本文算法可以更加科学、迅速、精确地制定新的调度计划，执行效率高，优化效果好，结果展示清晰。

5 结论

本文主要研究输出型煤炭码头船货匹配下泊位动态分配问题多目标优化模型及遗传算法。在模型方面，本文综合船舶、泊位、堆场、取装线、煤种、航道开放时间和装船作业规则等要素，构建了堆场-取装线-泊位-船舶联合分配优化数学模型；在算法方面，本文给出了遗传算法的详细设计，包括组合式编码、采用仿真推演策略的解码方法，追加了合法性检查的染色体生成算法，适应值函数设计，以及采用多种策略的遗传操作等。最后，针对黄骅港煤炭码头实例测试结果表明：模型实用性强，算法求解效率高，优化效果好且适用。本研究成果为解决具有船货匹配、动态调度、多约束、多目标等特点的复杂、大型输出型煤炭码头泊位动态分配问题提供了新的解决途径。