开放式多中心需求可拆分VRP及混沌遗传模拟退火算法

范厚明， 徐振林， 李 阳， 杨 翔

(大连海事大学 交通运输工程学院，辽宁 大连 116026)

0 引言

开放式多中心需求可拆分车辆路径问题(Open Multi-Depot Split Delivery VRP，OMDSDVRP)允许车辆从任意配送中心出发，完成配送任务后就近返回配送中心，同一个客户允许被多辆车进行访问。

Gulczynski等[1]首次提出多中心需求可拆分车辆路径问题(Multi-Depot Split Delivery VRP，MDSDVRP)问题，利用文献[2]的方法建立数学模型，然后采用文献[3]中的巡回算法优化路径。Soeanu等[4]设计了启发式算法对MDSDVRP问题进行求解。Ray等[5]的研究与文献[1]不同的是，在文献[5]中同一客户既可以由不同配送中心也可以由同一配送中心的不同车辆进行配送。Wang等[6]研究了MDSDVRP问题，设计三阶段启发式算法进行求解。

综上，以上参考文献还有以下几点未考虑：

(1)多配送中心车辆路径问题，先将客户进行分组，然后进行路径规划，易导致客户划分不合理，配送中心资源不能合理利用等情况。

(2)需求可拆分的车辆路径问题，不应限制每次访问客户的车辆来源，即来自不同配送中心的车辆也可对同一客户进行多次访问。

(3)多中心车辆路径问题，不应限制车辆完成配送任务后返回的配送中心，就近返回既能降低配送成本，又能实现资源共享。

(4)载重对于油耗的影响至关重要，忽略载重的变化，不能切实反映实际能源消耗。此外，针对需求可拆分的车辆路径问题，应考虑理货成本对总成本的影响。

结合以上未考虑的因素，对开放式多中心需求可拆分车辆路径问题(OMDSDVRP)展开研究。

1 OMDSDVRP的提出

图1(a)为传统VRP问题示意图，当车辆载重不足，则返回配送中心进行补货；图1(b)为需求可拆分VRP问题示意图，当车辆载重不足，可先服务客户的部分需求，剩余需求由下一辆车进行服务；图1(c)为MDSDVRP问题的示意图，允许来自不同配送中心的车辆对同一客户进行服务，车辆服务完成后，返回原配送中心；图1(d)为本文研究的OMDSDVRP问题示意图，允许来自不同配送中心的车辆对同一客户进行服务，车辆服务完成后，返回就近的配送中心。

2 问题描述及模型建立

2.1 问题描述

假设配送网络有完备的有向图：配送网络中所有节点集合V=D∪C∪0={0,1,…,m,m+1,…,m+n}，其中D={1,2,…,m}代表配送中心集合，C={m+1,m+2,…,m+n}代表客户集合，K={1,2,…,k,…|K|}代表配送车辆集合。0为虚拟配送中心，其与其他配送中心的距离为0。E={(i,j)|i,j∈V}代表配送网络中所有边的集合。di代表客户i点的配货需求量，Q代表配送车辆的额定装载量，dij代表两点之间的直线距离，ω代表道路迂回系数。tj代表客户j被配送车辆访问的次数，sjk代表配送车辆k配送给客户j的货物数量。Ci代表配送中心的日均建设成本，Ck代表配送车辆的固定成本，Ci代表配送车辆服务一次客户的理货成本。xijk表示配送车辆k是否从点i到点j。yij表示服务客户j的车辆是否来自配送中心i。

2.2 油耗成本分析

油耗成本受配送车辆服务客户的方向影响较大，其主要原因是配送装载量的变化。图2展示了配送方向对油耗的影响。

(1)

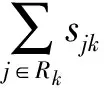
由于配送车辆油耗率受路况的影响，则油耗率可用式(2)表示。

(2)

φij代表节点i到节点j的道路状况系数，φij=1，表示道路通畅；φij>1，表示道路拥堵。

综上，配送车辆的油耗成本为:

Cijk=c·rijk·dij

(3)

其中c为油价。

2.3 模型建立

综上分析，本文建立的模型如下:

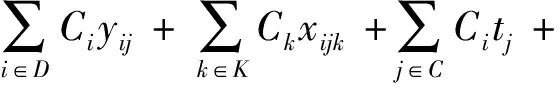
(4)

(18)

式(4)以配送中心日均建设成本、车辆固定成本、理货成本和油耗成本之和最小为目标；式(5)表示每个客户最少被配送车辆访问一次，最多被配送车辆访问两次；式(6)表示对于任一个客户，最少有来自一个配送中心的车辆对其进行服务；式(7)表示进入该点的车辆数量等于离开该点的车辆数量；式(8)表示每条配送路径的起止点都是虚拟中心0；式(9)表示从配送中心派出的车辆数限制；式(10)表示车辆的载重限制；式(11)表示两个配送中心之间没有路径连接；式(12)表示每辆车最多从一个配送中心出发，且只有一条服务路径；式(13)为子回路消除约束；式(14)表示有路径连接客户与配送车辆出发时的配送中心；式(15)表示任一配送中心都能满足客户的配货需求；式(16)表示车辆对客户的配货量应大于0；式(17)、(18)定义决策变量取值。

2.4 最优解理论

Dror等给出关于SDVRP的最优解定理，结合文献[3]中的定理，给出以下定理及证明。

定理若客户点之间的距离符合三角形不等式规则，则任意两条配送路径最多有一个拆分点。

证明如图3(a)所示，d1和d2为客户点C1、C2的配货量，配送路径Ra和Rb对C1、C2的配货量是d1a、d1b、d2a、d2b。

图3(b)中将Ra路径上的d2b转至Rb，同时将Rb上的配货量d2b转至Ra。图3(c)为各路径的配送方案，可以看出C1由Ra和Rb共同服务，C2只由Ra服务。

3 混沌遗传模拟退火算法

本文设计混沌遗传模拟退火算法对OMDSDVRP问题进行求解。

在初始解生成过程中引入混沌系统，以增加解的多样性、遍历性，式(19)为Logistic映射方程:

xn+1=rxn(1-xn),n=1,2,…

(19)

其中r∈(3.57,4]，xi∈[0,1]。

本文采用整数编码方式，算法流程见3.1节。

3.1 算法具体描述

步骤1参数设置。

步骤2路径编码。包括全路径编码和子路径编码。

步骤3初始化种群。

步骤3.1用式(19)生成Logistic映射初值。

步骤3.2产生初始种群。

步骤4令gen=1，把初始种群视为当代种群。

步骤5取第一条染色体生成配送方案。

步骤6计算各子路径上车辆访问的第一个和最后一个客户到各配送中心的距离，根据就近原则返回配送中心。

步骤7计算该染色体的总行驶距离。

步骤8重复执行步骤5～7，得到每条染色体的总行驶距离。

步骤9若当代最优染色体的总行驶距离小于历史最优总行驶距离，则接受该染色体；否则，拒绝。

步骤10解的扰动。本文采用三种变邻域操作，并设计自适应进化压力和邻域半径搜索策略提高搜索效率：

(2)引入邻域半径搜索策略，提高求解效率，具体流程见3.2节。

步骤11更新解。采用Metropolis准则接受较差的解。

步骤12重复步骤4～11，直到gen>MAXGEN。

3.2 解的扰动策略

(1)0-1 Exchange。随机选择2个客户，把第二个客户插入到第一个客户的前面。

(2)1-1 Exchange。随机选择2个客户并互相交换位置。

(3)2-opt。随机先选择2个作用弧，交换每个作用弧上其中一个客户的位置。

(4)邻域半径搜索策略[7]。

步骤1设置range为客户o的邻域搜索半径，其中range=3～8；

步骤2计算dij；

步骤3range个与客户i最近的客户被挑选出，组成搜索范围。

4 算例验证及结果分析

本文设置参数pop_size=200～1000，MAXGEN=50～1000，r=4。

实验1取文献[8,9]中的算例进行求解，表1给出了求解结果，就总行驶距离而言，本文算法比文献[8]改进了7.09%，比文献[9]改进了1.23%。实验结果表明本文使用网络化联合配送方式，具有较好的求解效果。

表1 实验1结果分析

采用文献[8]中的算例，用本文设计的算法与其他几种启发式算法进行比较，实验结果如表2所示。实验结果表明：本文设计的算法具有较强的求解性能、稳定性较好。

表2 实验1结果对比

实验2对文献[10]中客户规模为30～50的算例进行求解，与文献[10]的对比结果如表3所示。实验结果表明：本文设计的混沌遗传模拟退火算法能找到9个算例的已知最优解，文献[10]中的两种算法均未找到已知最优解。本文设计的混沌遗传模拟退火算法的平均偏差为0.67%，均小于其他两种算法，再次证明算法的稳定性。

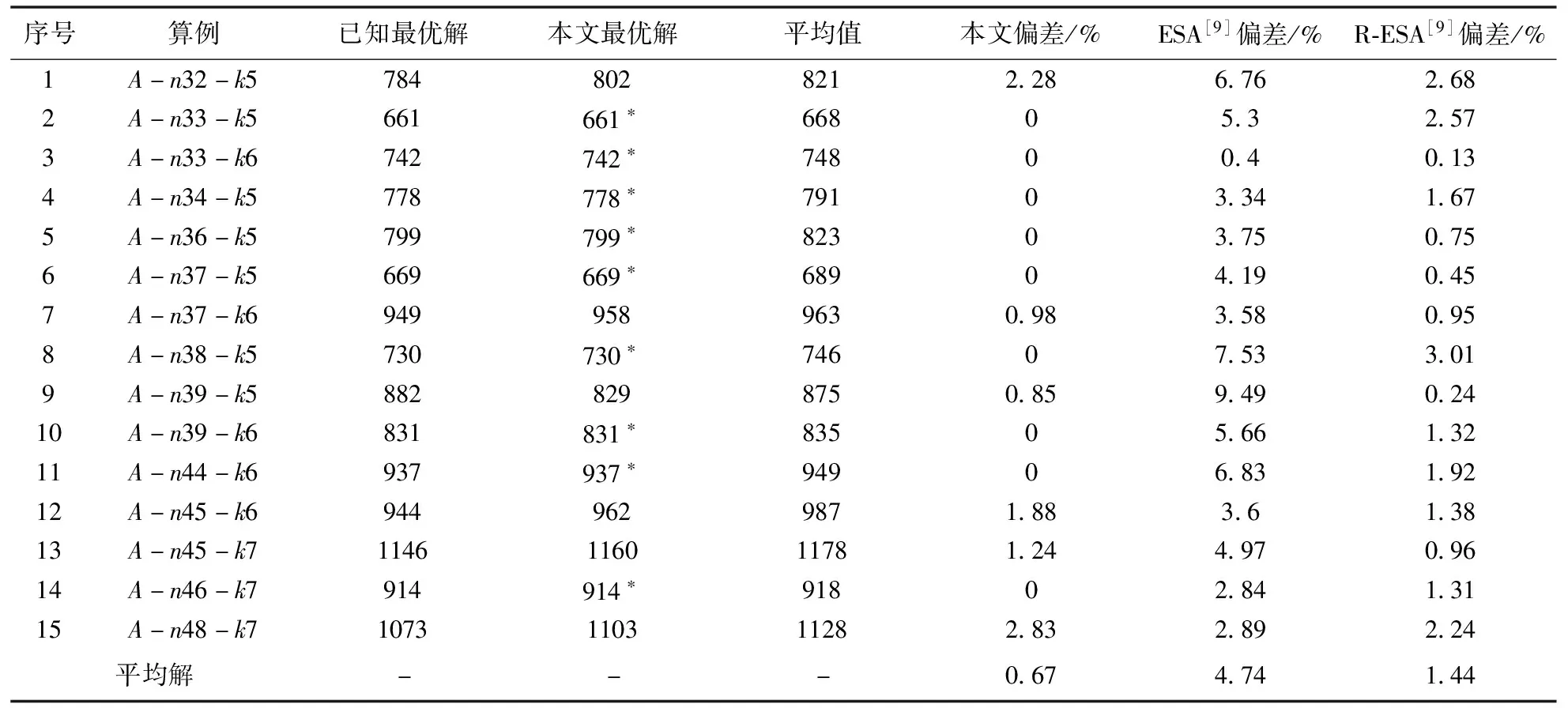
表3 实验2结果对比

实验3对MDVRP标准算例进行测试，与文献[11]的对比结果如表4所示。实验结果表明：本文设计的混沌遗传模拟退火算法的平均偏差为0.26%，小于GRASP/VND，证明了本文算法的稳定性。

表4 实验3结果对比

算例p01、p02最优行驶路径以及最短路径变化趋势如图4所示，其中1～4代表配送中心，5～54代表客户。

实验4用文献[8,9]中算例文献[10]和本文设计的算法进行分析，对比结果如表5所示。实验结果表明：文献[10]设计的算法与本文算法的求解质量相差不多，但本文算法的自适应进化压力和邻域半径搜索策略提高了求解效率。

表5 实验4不同算法求解结果统计表

表6展示了以下四种算法的求解结果。图5为收敛迭代图。

表6 四种算法运行结果比较

实验5对文献[12]中算例SQ1进行修改，修改如下：Q=10t，客户需求量也相应修改，u1=0.15L/km,u2=0.4L/km,c=6,ω=1.2,Ci=20,Ck=5,Ct=2.5,φij∈[1,1.25]。

表7展示了本文算法对以下三种模式的求解结果。实验结果表明：OMDSDVRP模式的总配送成本最低，MDVRP模式的总配送成本最高。OMDSDVRP模式实现了车辆资源和客户资源的整合，再次验证了本文模型的有效性。

表7 实验5结果对比

5 结论

本文针对OMDSDVRP进行了研究，主要结论如下：

(1)OMDSDVRP模型充分利用各配送中心的资源，实现了资源共享。

(2)混沌遗传模拟退火算法引入混沌系统增加初始解的多样性，自适应进化压力和邻域半径搜索策略提高求解效率。

(3)通过对多组不同规模不同类型的算例进行求解，验证了本文算法具有较强的搜索性能。