一种改进的人工电场算法*

李晓瑜

（安康学院电子与信息工程学院 安康 725000）

1 引言

元启法式算法是通过一些定义规则和随机性来模拟自然现象或生物进化的过程进行优化的算法［1］。由于元启法式在解决复杂非线性，多模，杂交和组合等问题时具有较优的性能，因此吸引了许多的研究者对其进行研究，各种基于种群的元启发式算法不断被提出例如，遗传算法（GA）［2］，差分算法（DE）［3］，人 工蜂 群 算 法（ABC）［4］，蚁 群 算法（ACO）［5］，粒子群算法（PSO）［6］，万有引力算法（GSA）［7］和布谷鸟算法（CCS）［8］等。不同的算法有不同的优势，“天下没有免费的午餐”［9］，一些作者提出了一些杂交的算法［10～11］。

人工电场算法是受库仑定律和运动定律启发，由Anita 和Anupam Yadav 等在2019 年首次提出来的一种基于种群的元启发式优化算法［13］。人工电场算法将种群中的每个个体看作一个电的粒子，每个粒子所处的位置代表问题的一个候选解，这些粒子在电场力的作用下不断改变其位置，来寻找个体的最优位置也就是问题的最优解。人工电场算法的性能主要受粒子间电场力的影响，粒子间的电场力决定粒子的速度和加速度，从而影响粒子移动的速度和方向。

电场力越大，粒子位置改变的幅度越大，算法探索新的可行域的范围越广，算法的勘探能力就越强。电场力越小，粒子位置改变的幅度越小，算法可以开采邻域区域，有利于算法的开采能力。在AEFA 算法中粒子间的电场力的大小除了受到粒子间距离和带电量的影响外还受到引力常数的影响。引力常数的取值越大，粒子间的电场力越大，引力常数越小，粒子间的电场力也越小。基于种群的元启发式算法的健壮性和有效性是由在算法的探索和开采能力之间平衡的能力来决定的［14］。在算法的初始阶段搜索空间中的解一般离最优解的距离比较远所以个体需要较大的移动步长，也就是需要加强个体的探索能力；在算法后期最优解一般位于当前的个体的临近区域，所以需要减小个体的移动步长，来增强个体的局部开采能力，避免错过最优解［15］。在最初的AEFA 算法中采用一个递减的指数函数来计算引力常数，这种计算方法会使引力常数的取值快速的减小，从而使得算法探索的时间不足，容易使算法陷入局部最优，本文在通过对引力常数的计算方法进行改进，初始阶段使得引力常数K 有一个较大的值，然后使其缓慢的减小，使得算法有充足的时间在搜索空间中进行探索，在算法的后期引力常数取一个较小的值，使得算法能够进行局部开采功能，获取最优解。

2 人工电场算法（AEFA）

库伦定律规定两个带电粒子间的电场力与粒子所带的电量成正比，与粒子间的距离成反比。假如两个粒子的带电量分别为Q1和Q2，引力常数用K 来表示，粒子间的欧氏距离用D 来表示，则粒子间的电场力F可用公式表示为

在牛顿定律中，物体的加速度与它所受的合力成正比，与它的质量成反比。如果加速度用a 表示，粒子的质量用m 表示，粒子间的合力用F 表示，则加速度计算公式为

人工电场算法（AEFA）是一种基于种群的元启法式优化算法，通过模拟库仑定律的特点来解决优化问题。在AEFA 中每个个体是一个带电的粒子，每个粒子的位置代表问题的一个解，这些带电的粒子在它们之间的电场力的引导下，逐步的向种群中最优的位置靠近，这个最优的位置就是我们要找的最优解。在AEFA 算法中电量较小的粒子在电量较大的粒子的引力下，向带电量较大的粒子移动。在引力的不断作用下，整个种群逐渐向电量较大的个体方向逼近，最终搜索到问题的最优解，并且个体的运动遵循牛顿第二定律。

其中，K0是库伦常数的初始值，α是一个常数值，it表示当前代数，maxit表示最大迭代次数。在AEFA 算法中粒子的带电量越大，它所在的位置代表的解越优。第i个个体所具有的电量的可使用如下公式计算：

粒子i在第d 维所受到的合力以及所具有的加速度可分别表示如式（11）和式（12）：

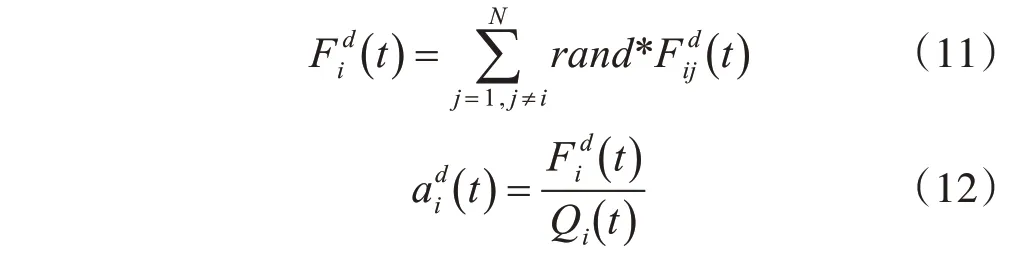
其中，rand 是一个取值范围在0～1 之间的服从均匀分布的随机数。

粒子在电场力的作用下不断的更新位置，逐渐向最优解靠近。

3 改进的引力常数

为了平衡AEFA 算法的探索和开采能力，使得库仑常数在算法初期有一个较大的数值，使得粒子在搜索空间的移动步长足够大，这样可以提升算法的探索能力，使得算法在较大的空间搜索最优解，而且使得库仑常数以相对缓慢的速度递减，这样可以使得算法充分的探索搜索空间。在迭代的后期库仑常数取一个较小的值，粒子以较小的步长在搜索空间进行移动，这样可以使得算法增强算法的局部开采能力，避免错过最优解。新的库仑常数计算公式如下：

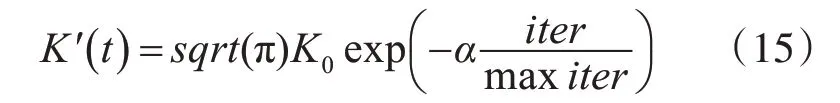
K′(t)和K(t)的对比图如图1 所示。其中黄色曲线代表的是K(t)，蓝色曲线代表的是K′(t)。

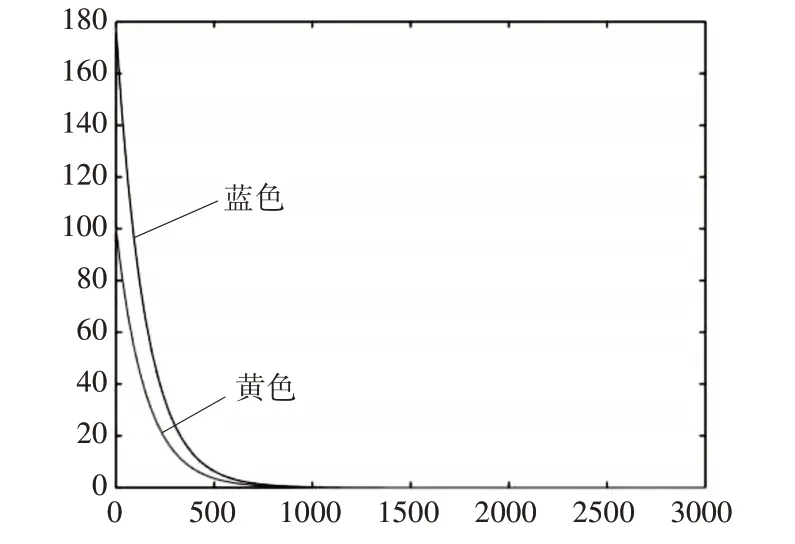
图1 库仑常数对比图

4 实验结果分析

为了证明改进后算法的有效性，将IAEFA 与AEFA 在三个基准测试函数，包括两个单模函数（F1-F2）和一个多模函数（F3）上进行对比，我们采用表示解的精度的平均值和表示解的稳定性的方差来对算法结果进行评估。实验设置如下：种群规模为50，问题的维度为30，最大迭代次数为1000，为了算法的公平性每个算法在每个函数上独立运行25次。F1，F2和F3的3D图像如图2～4所示。

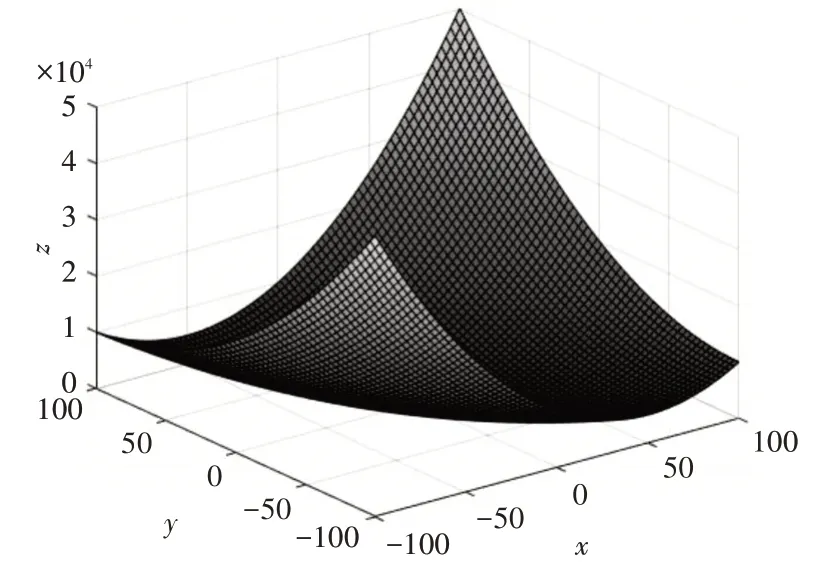
图2 F1 Schwefel's 函数

AEFA和IAEFA的实验结果如表2所示。

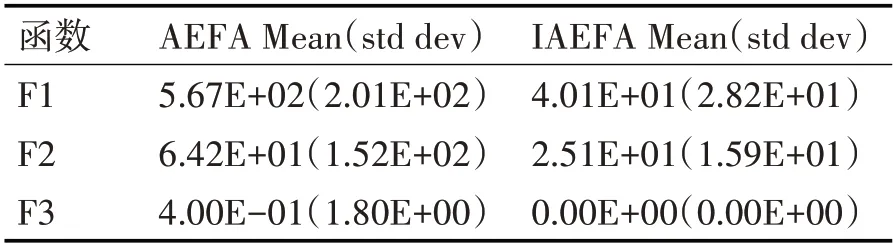
表2 解的对比结果

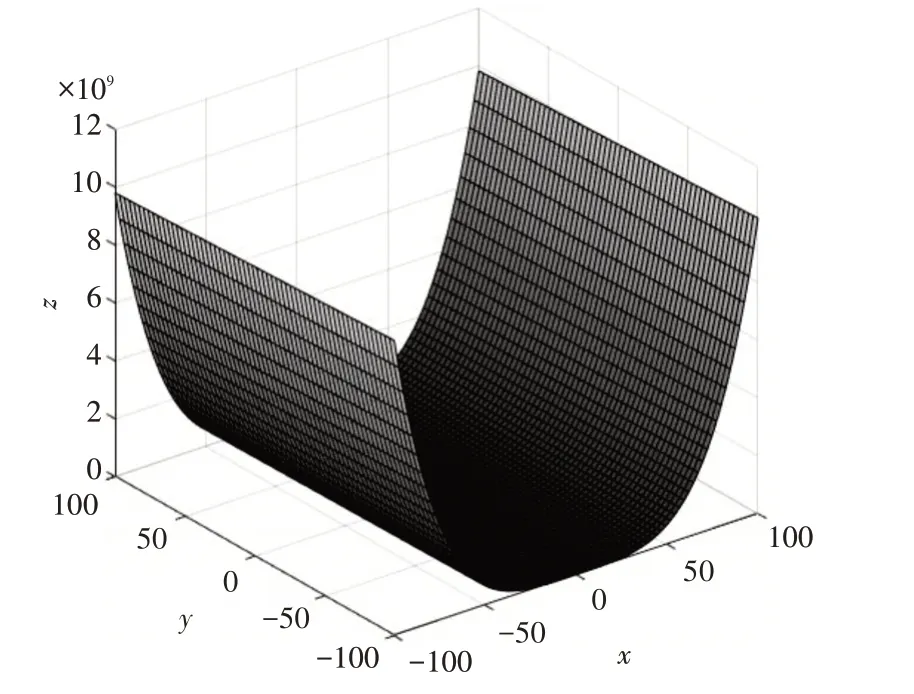
图3 F2 Rosenbrock函数

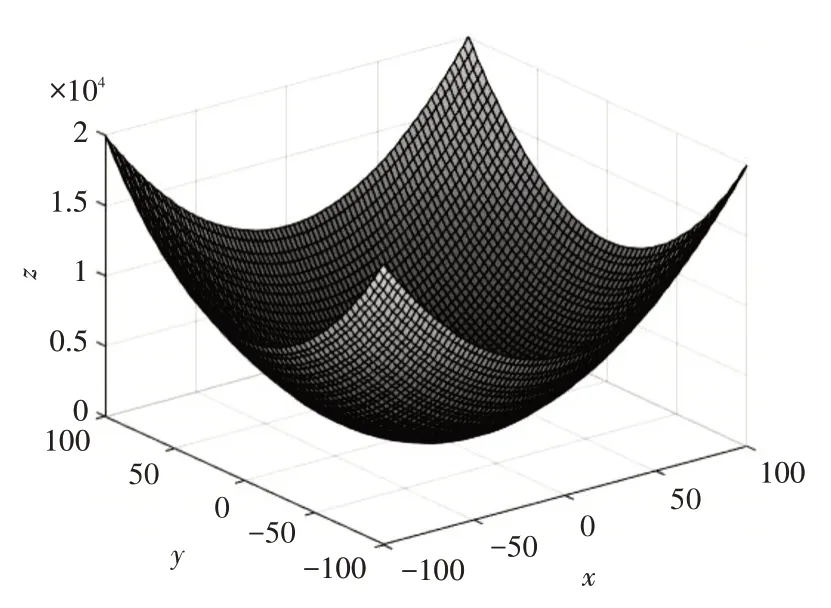
图4 Set Function 函数

由表1 中结果可以看出，IAEFA 在所有测试函数上的结果都优于AEFA。为了进一步验证改进后算法的有效性，我们对IAEFA 和AEFA 两种算法的收敛性进行对比分析。其对比结果如图5所示。

表1 基准测试函数

通过对比发现改进后的算法无论在求解精度和收敛速度上均有提高。

5 结语

本文通过分析AFEA 算法的工作原理，对影响其性能的引力常数进行改进，通过减缓引力常数变化的速度来延长算法勘探的过程，延长算法勘探新的可行区域的时间，提升算法的勘探能力，促进算法寻找到更多的可行解。并将改进后的算法和原始的AFEA 算法在三个经典测试函数上进行性能对比，对比结果显示改进后的算法在收敛速度和解的精度方面都有很大的提高，这表明本文提出的改进算法是有效的。