关注知识本质 巧用转化思想
李燕华

“平面图形的认识(二)”是在“平面图形的认识(一)”的基础上,对平行线和角的关系的进一步研究,介绍了图形的平移特征及三角形、多边形的基本知识。善于关注知识的本质,巧妙运用转化思想,能帮助我们轻松找到解决问题的线索。
一、抓住平行线的本质
1.如图1,将一块含有60°角的直角三角板放置在两条平行线上,若∠1=45°,则∠2为( )。
A.15° B.25° C.35° D.45°
【解析】正确作出辅助线,熟练运用“两直线平行,内错角相等” 是关键。如图2,我们观察发现,60°的角在两条平行线之间,并与∠1、∠2是异侧关系,于是,过三角形的60°角的顶点F作EF∥AB,先根据平行线的性质推出∠EFG=∠1=45°,进而求出∠EFH=15°,再求出∠2=15°。
2.如图3,一束光线AB先后经平面镜OM、ON反射后,反射光线CD与AB平行,当∠ABM=40°时,∠DCN的度数为( )。
A.40° B.50° C.60° D.80°
【解析】此题考查了平行线的性质及物理中的“入射角等于反射角”,熟记“两直线平行,同旁内角互补”是解题的基础。平面镜反射时,由“入射角等于反射角”,得∠OBC=∠ABM=40°,从而得∠ABC=180°-∠ABM-∠OBC
=100°。根据“两直线平行,同旁内角互补”,得∠BCD=180°-∠ABC=80°,从而得∠BCO=∠DCN=[12](180°-∠BCD)=50°。
二、理解三角形基本概念
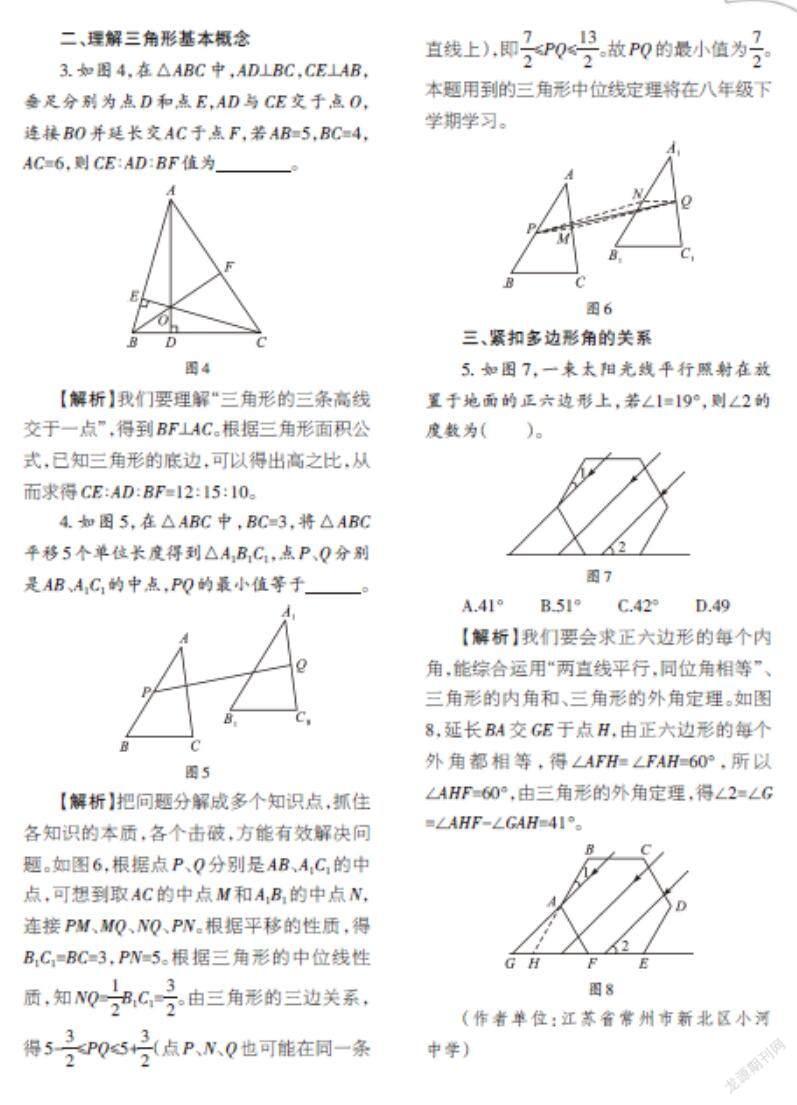
3.如图4,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D和点E,AD与CE交于点O,连接BO并延长交AC于点F,若AB=5,BC=4,AC=6,则CE∶AD∶BF值为 。
【解析】我们要理解“三角形的三条高线交于一点”,得到BF⊥AC。根据三角形面积公式,已知三角形的底边,可以得出高之比,从而求得CE∶AD∶BF=12∶15∶10。
4.如图5,在△ABC中,BC=3,将△ABC平移5个单位长度得到△A1B1C1,点P、Q分别是AB、A1C1的中点,PQ的最小值等于 。
【解析】把问题分解成多个知识点,抓住各知识的本质,各个击破,方能有效解决问题。如图6,根据点P、Q分别是AB、A1C1的中点,可想到取AC的中点M和A1B1的中点N,连接PM、MQ、NQ、PN。根据平移的性质,得B1C1=BC=3,PN=5。根据三角形的中位線性质,知NQ=[12]B1C1=[32]。由三角形的三边关系,得5-[32]≤PQ≤5+[32](点P、N、Q也可能在同一条直线上),即[72]≤PQ≤[132]。故PQ的最小值为[72]。本题用到的三角形中位线定理将在八年级下学期学习。
三、紧扣多边形角的关系
5. 如图7,一束太阳光线平行照射在放置于地面的正六边形上,若∠1=19°,则∠2的度数为( )。
A.41° B.51° C.42° D.49
【解析】我们要会求正六边形的每个内角,能综合运用“两直线平行,同位角相等”、三角形的内角和、三角形的外角定理。如图8,延长BA交GE于点H,由正六边形的每个外角都相等,得∠AFH=∠FAH=60°,所以∠AHF=60°,由三角形的外角定理,得∠2=∠G=∠AHF-∠GAH=41°。
(作者单位:江苏省常州市新北区小河中学)

