改进的粒子群算法求解函数极值研究

钱泽钜

（西藏民族大学 陕西 咸阳 712082）

0 引言

在求解函数极值的问题中，当函数比较简单时，可以通过直接求解求得极值。但是，大部分函数是无法通过直接求解求得极值。这时就需要用到智能算法，在一个解空间中寻找最优极值解。

传统的智能算法包括遗传算法、粒子群、鱼群算法等。其中，粒子群算法有简单易行、收敛速度快、设置参数少等优点。所以，本文采用粒子群算法来解决函数求极值的问题。

1 标准粒子群算法

粒子群算法的思想来源于对鸟类捕食行为的研究，模拟大的鸟群落通过协同合作的捕食行为。行为基础就是共享自身与种群信息，根据此基础来判断食物所在。

1.1 粒子群算法简介

鸟群中有很多只鸟，而每一只鸟都是一个问题，称为“粒子”。每个粒子在一个空间内进行搜索。其所在位置的好坏是由适应度函数决定的，也就是fitnessfunction。而且，每个粒子需要有记忆性和速度以决定飞行的位置与方向。这就需要粒子根据自身的经验与群体的经验来决定[1-2]。

1.2 粒子群算法的实现步骤

（1）初始化种群。初始化，包括要达到的群体规模N。每一只鸟，也就是每一个粒子随机初始化位置向量Xi，随机初始化速度向量Vi。

其中Xi=（xi1，xi2，…，xiD），Vi=（vi1，vi2，…，viD）。

（2）将初始生成的随机位置向量中每一个xi代入所要求极值的函数f（xi），所求的函数极值就是适应度值Fitness（i）。

（3）计算初始化的粒子的适应度值，将最开始计算的每个初始化粒子的适应度值储存为个体极值Pbest，将所有初始化粒子的个体极值Pbest进行比较，选择最优的作为当前全局最优，存入全局极值Gbest。

（4）算法开始迭代，每迭代一次，对于每一个粒子，用其适应度值Fitness（i）和与上一次迭代的个体极值Pbest作对比，如果Fitness（i）优于个体极值Pbest，就用适应度值Fitness（i）替代个体极值Pbest。如果Fitness（i）并不优于个体极值Pbest，则保留个体极值Pbest[3-4]。

（5）对于每一个粒子，用其适应度值Fitness（i）与上一次迭代的全局极值Gbest作对比，如果Fitness（i）优于全局极值Gbest，就用Fitness（i）替代全局极值Gbest。如果Fitness（i）并不优于全局极值Gbest，则保留全局极值Gbest。

（6）更新粒子的位置Xi与速度Vi

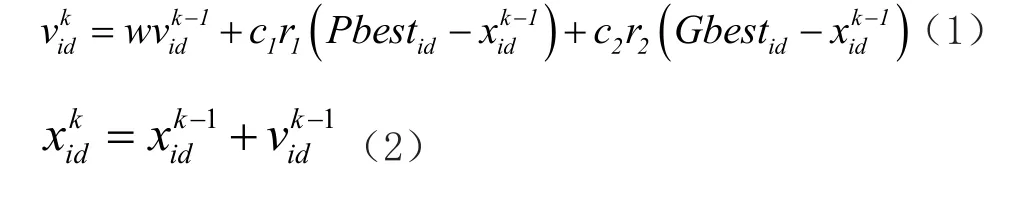
其中，ω为惯性因子，较大的ω拥有较强的全局搜索能力，较小的ω拥有较强的局部搜索能力。c1与c2为学习因子，也称为加速常数，其中c1是个体部分，如果c1过小，则容易陷入局部最优。c2集体部分，如果c2过小，会导致算法收敛速度变慢。r1，r2为[0,1]范围内的均匀随机数。为上一次迭代的粒子位置，为上一次迭代的粒子速度。为本次迭代的粒子位置，为本次迭代的粒子速度。

（7）如果满足最大循环次数的条件，则停止循环，如果不满足，则返回步骤（4）。

算法框如图1所示：

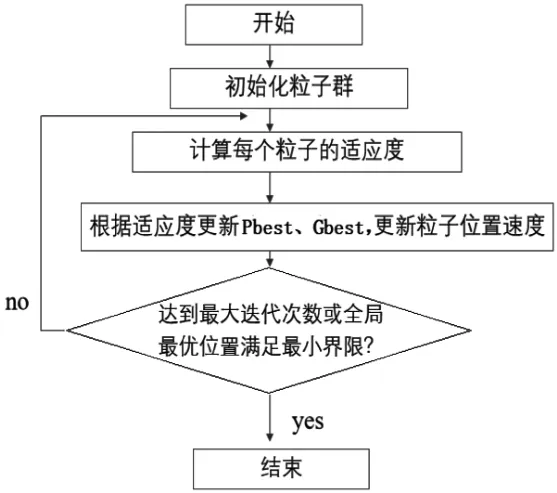
图1 传统粒子群算法流程

2 改进粒子群算法解决函数求极值问题

2.1 算法的改进

将算法进行分层，分为两层，第一层负责算法前期，并且混合遗传算法，用来扩大搜索范围；第二层负责算法后期，主要用作精准搜索，加速收敛。这样做，就可以将一个矛盾复杂的要求，分解成两个小的部分，各司其职，来完成算法的搜索[5]。混合粒子群算法，就是将其他优化算法的一些技术应用到粒子群算法之中，用于提升粒子的多样性，使其可以跳出局部最优，增强全局寻优的能力，本文采用遗传算法中的杂交概念，混合入粒子群算法。针对传统的固定惯性因子ω，无法兼顾算法前期与后期不同的要求，改为线性递减的惯性因子ω。其公式为：

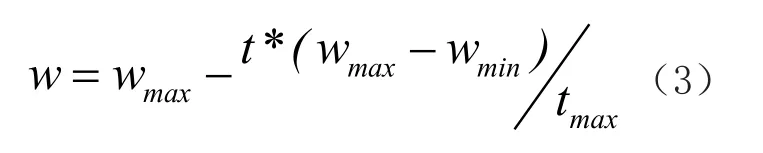
其中，wmax为惯性因子的最大值，wmin为惯性因子的最小值，t为迭代次数，tmax为最大迭代次数。

2.2 基于杂交的粒子群算法

该算法是借鉴了遗传算法中的杂交概念[6]，在每次的迭代之中，根据杂交的概率[7-8]，首先选择一定量的粒子作为父代粒子放入到杂交池子中，让池子中的粒子进行杂交操作，产生与父代粒子个数相同的子代粒子，并用产生的子代粒子替换父代粒子。

分层混合粒子群算法的实现步骤：

（1）在规定的范围之内，随机设置初始化粒子的位置与速度。

（2）计算初始化的粒子的适应度值，将最开始计算的每个初始化粒子的适应度值储存为个体极值Pbest，将所有初始化粒子的个体极值Pbest进行比较，选择最优的作为当前全局最优，存入全局极值Gbest。

（3）设置参数T，T小于最大循环次数。当算法循环次数小于T时，进入步骤（4），当算法循环次数大于T时，进入步骤（5）。

（4）对每个粒子的速度与位置进行更新。进入步骤（6）。

（5）对每个粒子的速度与位置进行更新。进入步骤（6）。

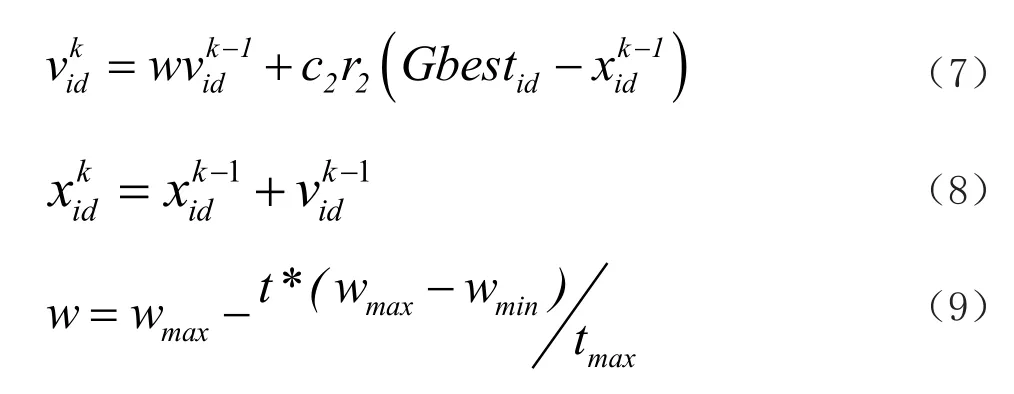
（6）计算每一个更新后的粒子的适应度值，将适应度值与粒子最好位置比较。更新全局极值Gbest。

（7）根据一定的杂交概率选取指定数量的粒子，并将选取的指定数量的粒子放入杂交池。将两个父代个体的部分进行替换重组构成新的个体，并用子代粒子替代父代粒子，子代的位置与速度为：

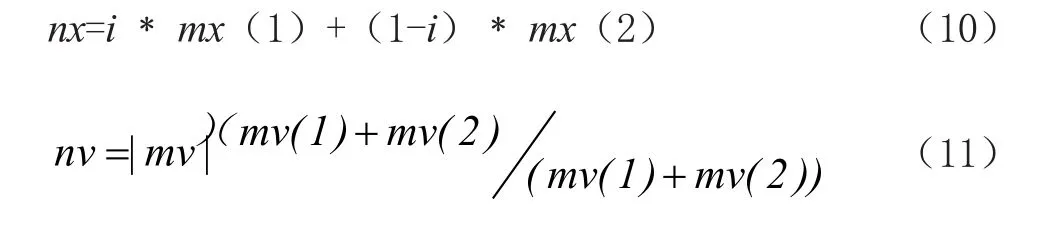
其中，保持Pbest和Gbest不变。mx（1），mx（2）为两个不同的父代粒子，nx为交叉操作后的子代粒子的位置，nv为交叉操作后的子代粒子速度，i是0到1之间的随机数。

（8）当如果满足结束条件（循环次数满足最大循环要求），则停止循环，如果不满足，则返回步骤（3）。

3 算法仿真测试

3.1 测试函数介绍

为了验证所提出算法是否有效，选取两个类型不同的函数，作为测试函数进行测试验证。

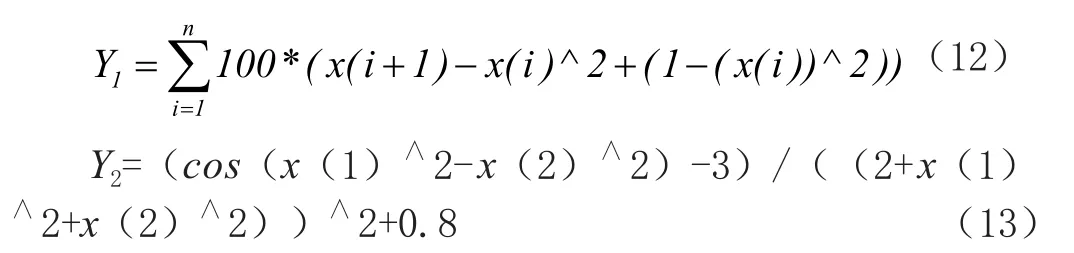
其中，Y1是一个多维函数，Y2是一个复杂的多模函数。通过传统的PSO算法与改进的PSO算法对两个不同类型函数的对比，来验证算法是否有效。

3.2 算法仿真

对出传统的PSO算法，初试种群选择为50，c1与c2学习因子设置为2，ω惯性权重设置为0.8。改进PSO算法，Y1中设置T为10，Y2中设置T为100，除了w惯性权重设置不同外，其余设置与传统PSO算法设置相同，其中，惯性权重w设置为区间[0.6,0.8]。在测试函数时，式（1）取最大迭代次数为100，式（2）取最大迭代次数为1 000，对两个函数各优化10次。算法是否可以快速稳定的收敛，是否可以跳出局部最优得到全局最优，可以衡量一个算法是否优秀。越快收敛，且能跳出局部最优，说明快速有效的求解函数极值。通过对比收敛结果与收敛速度，来展示改进算法的有效性，结论如表1和图2所示：

图2 测试函数适应度值变化

表1 测试函数优化结果

通过以表1、图2可以看出，改进PSO算法对比传统PSO算法在收敛速度与收敛结果这两个方面，新算法收敛速度更快。在收敛结果上，新算法也拥有更好的稳定收敛结果。

3.3 仿真结果

从上图可以看出，改进的粒子群算法与传统粒子群算法相比，有比较明显的优势。对于测试函数Y1改进的算法收敛速度更快，基本在10步左右就可以收敛，收敛速度快，说明算法求解函数极值的速度快。即便算法前期陷入局部最优解，也可以很快地跳出局部最优。而传统算法侧需要35次左右才能收敛，对比改进的算法，收敛速度慢一些，说明算法求解函数极值慢一些，而且，陷入局部最优解时，跳出局部最优比较慢。而收敛结果，改进算法可以稳定收敛到0.3。但传统算法却无法稳定收敛，在0.3附近波动。对于测试函数Y2，改进算法在100步左右就可以收敛，收敛速度快，且稳定收敛。而传统算法则需要250步左右才能收敛，收敛速度不如改进算法，收敛缓慢，且陷入局部最优。

4 结语

本文提出的改进粒子群算法，是先通过对算法进行分层，再局部融合其他智能算法，同时采取自适应权重的方法实现的。在算法前期，扩大搜索范围，避免陷入局部最优；在算法后期，加速算法的收敛，并用于解决函数求极值的问题。实验结果表明，改进的粒子群算法整体性能良好，可用于求解其他函数求极值的问题。