基于CSI的日常行为识别方法

周 祥，常 俊，武 浩

(云南大学 信息学院，云南 昆明 650091)

0 引 言

传统的基于传感器[1-5]的行为识别方法，需使用者佩戴各种传感器设备，使得使用者感到不便，而基于如视频图像[6]、雷达[7]等无设备的方式，前者由于不利于保护隐私同时对环境光照的要求较高，后者成本较高不利于广泛使用。而现如今基于WiFi信号的行为识别方法则有着成本低、识别精度高等特点。其中基于WiFi信号的接收信号强度(RSSI)[8]的行为感知，因其不能表征细粒度的信息，所以对人体行为的识别效果并不理想。而CSI信号[9]相比RSSI信号，其是细粒度的信号特征信息，每个CSI值代表正交频分复用(OFDM)系统[10]中子载波的幅度和相位，所以其含有更高的数据分辨率。如Thomas等[11]对CSI信号提取基于语音信号的梅尔频率倒谱系数(MFCC)特征[12]，再结合采用CNN[13]用于CSI时间序列分类，实现了95%的平均识别率，Akhtar等[14]从经过处理后的CSI信号无线电图像的判别分量中提取特征用于识别驾驶员行为，实现了94.1%的平均识别精度。还有Yao等[15]采用小波变换[16]提取CSI信号时频域特征用于行为识别，得到了93.1%的平均识别精度,可见对于CSI用作行为识别具有很好的应用价值。

现如今基于信道状态信息的行为识别工作中，由于硬件限制，所以很少关注CSI信号测量中普遍存在的线性相位误差，从而忽略了信息有用的非线性特性，以及对信号进行预处理难免会滤除一些有用信息，从而影响识别的精度。针对这一问题，提出一种基于WiFi信道状态信息的行为识别方法，通过从原始CSI信号中提取代表信号非线性特性的三阶累积量[17]作为特征，并采用一种基于互信息的特征选择技术(MIFS)[18]对原始特征进行筛选提取考虑到非高斯信号分布的高鲁棒性特征子集，最后将提取到的特征子集输入到经过了粒子群优化算法(PSO)[19]优化过参数的SVM分类模型[20]中。该方法有着较低的系统复杂度，能实现较高的识别精度和鲁棒性。

1 系统原理

1.1 CSI模型原理

无线信号在传输过程中由于其信道状况并不稳定，会根据环境因素而发生衍射、反射、散射等变化，这些变化会反映到接收端接收的子载波的波动中，无线信号在空气中的传播如图1所示。而现如今引入正交频分复用(OFDM)的无线技术的最新发展实现了具有最小误码率(BER)的更高数据包传输速率。符合IEEE 802.11n OFDM标准的商用Wi-Fi设备还实现了多输入多输出(MIMO)概念。在Linux 802.11n CSI工具中，符合OFDM的设备可以将信道频率响应(CFR)读取为CSI信号，其主要反映了子载波的信号幅度和相位的变化。Wi-Fi的信道模型可以表示为

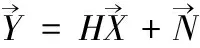
(1)

H=(hijk)NT×NR×30

(2)

其中，i∈[1,NT]，j∈[1,NR]，k∈[1,30]。 而hijk表示第i根发射天线到第j根接收天线之间的数据流中的第k个子载波的值。其具体还可以表示如下

hijk=|hijk|ej∠hijk

(3)

其中， |hijk| 表示幅度响应， ∠hijk表示相位响应。

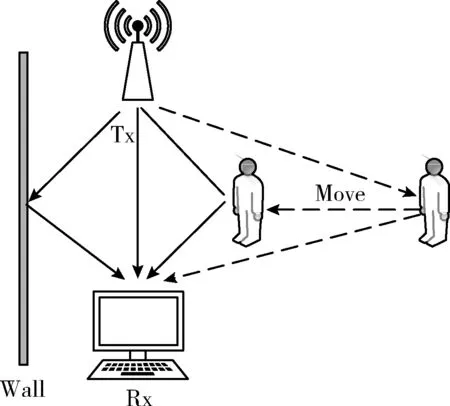
图1 无线信号传播

1.2 三阶累计量

首先高阶累积量对高斯噪声不敏感，所以在处理带有高斯有色加性噪声的非高斯信号时，可对其求高阶累计量，使得输出噪声部分的高阶累积量为零，只留下非高斯信号部分，从侧面增强了有用信号的信噪比，可见采用高阶累积量的特征可以免除信号预处理阶段，降低系统复杂度。而优选使用三阶累积量来从原始CSI信号中提取特征，是因为其相比一、二阶累积量其能揭示更丰富信号特征信息，四阶的累积量及其以上，因其建立了高度复杂的矩阵，需要大量的计算成本，所以在当前工作中不考虑它。而三阶累积量的具体推算过程如下：对于一个变量X存在一个距生成函数mkx(t)， 且当统计期望E{etX} 存在，t∈R。 此时可以得到函数高阶距表达式

mkx(τ1,…,τk-1)=E{X(t)X(t+τ1)…X(t+τk-1)}

(4)

其中，τ1…τk-1为时滞参数，由式(4)可推出三阶距的表示为

m3x(τ1,τ2)=E{X(t)X(t+τ1)X(t+τ2)}

(5)

而相对应的非零累积量Ckx， 可以计算为相应矩的非线性组合

Ckx(τ1,…,τk-1)=mkx(τ1,…,τk-1)-mkxG(τ1,…,τk-1)

(6)

其中，mkx(τ1,…,τk-1) 为k阶距，mkxG(τ1,…,τk-1) 为相应高斯过程的k阶矩，而特别的，若X(t) 具有零均值，三阶累积量可以表示为

C3x(τ1,τ2)=m3x(τ1,τ2)

(7)

1.3 MIFS算法原理

MIFS是一种基于互信息的特征选择算法，其使用互信息度量候选特征与类别之间的相关性，以及与已选特征集合的冗余性，再以贪心策略选择与类别相关性强且已选特征冗余度低的特征集合。从而可以减少计算时间，提高计算精度。而互信息定义如下

(8)

式(8)表示变量X和Y之间的互信息，其中p(x)、p(y)、p(x,y) 分别表示X的概率分布，Y的概率分布以及X和Y的联合概率分布。两变量之间互信息越大，之间相关性越强。依据互信息的定义，MIFS算法对应的算法流程如图2所示，具体步骤如下：

(1)初始化：将原始输入特征空间FR赋值给F，S置空；

(2)对F中每个输入特征fi， 根据式(8)计算互信息I(Fi;C)；

(3)选择使I(Fi;C)； 最大的那个fi， 将fi加入到S中，记为{fi}→S， 同时从F去掉fi记为F(〗fi}；

(4)重复以下过程，直到选够K个特征：

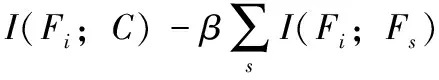
(5)输出包含选定特征的特征子集S。

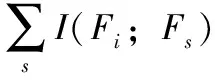
图2 MIFS算法流程

1.4 粒子群优化算法原理

当分类模型的参数属于最优时，相应的模型的分类精度最高，而粒子群优化算法(PSO)属于基于群体的智能优化搜索算法，可以用其优化支持向量机的分类模型(SVM)参数使其获得最高的识别准确率。首先生成初始化例子群，计算其适应值，并寻找个体极值pid和全局最优解pgd， 最终来更新粒子的速度和位置。而每个粒子根据下面的式(9)、式(10)来进行更新其速度和位置

(9)

(10)

其中，vid和xid分别代表速度和位置，r1和r2是0到1之间的随机数，c1为学习因子，c2为社会因子，而当社会因子大于学习因子时，有助于粒子向着全局最搜索，因此，取c1=1.6，c2=2。 而ω是权重，其取值范围为 [ωmin,ωmax]， 其中最大迭代次数为itermax， 由上可得到以下公式

(11)

由于本文选择的核函数是高斯核函数，所以将粒子群算法应用于支持向量机分类模型的参数寻优时，粒子就是惩罚因子C和核参数γ， 采用PSO调参就是寻找使SVM分类精度最大的参数，具体通过粒子群优化算法优化SVM分类模型的参数的流程如图3所示。

图3 PSO优化SVM参数流程

2 整体系统设计

系统整体设计包含4个模块：由数据采集模块、特征提取模块、特征选择模块、分类模型4部分组成，具体系统结构如图4所示，实验最初采集到不同环境下的不同动作的CSI原始数据，然后对数据提取其三阶累计量特征，再采用MIFS算法对原始特征进行筛选鲁棒性强的特征子集，将其输入到已经别粒子群优化算法优化过参数的支持向量机分类模型中采用10倍交叉验证，得出识别准确率。

图4 系统结构

2.1 原始数据采集

本次数据采集分别在长4 m，宽5 m的实验室和长4 m，宽6 m的会议室两种不同环境下采集，具体实验场景如图5所示，可见办公室场景环境相对复杂，而实验室场景的环境较为空旷。实验通过两台外置了Intell 5300网卡的台式机作为CSI信号的收发端，其中Tx表示信号发射端，Rx表示信号接收端，而发送端采用1根发送天线用以发送信号，而接收端采用3根接收天线用以接收信号，且设置了工作频率为2.4 GHz，带宽设置为20 MHz。而收发端距离地面高度为75 cm同时之间相距2 m。

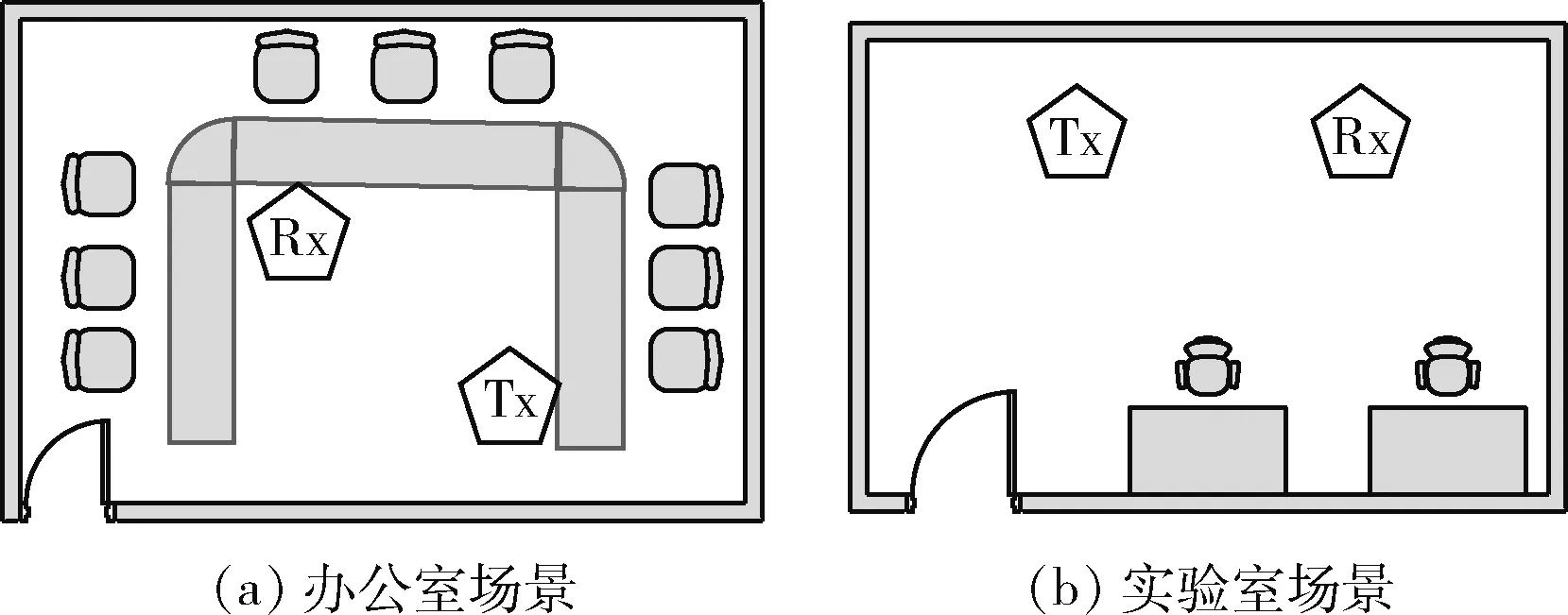
图5 实验场景

2.2 特征提取

本文采用了Matlab自带的高阶光谱分析工具箱(HOS)从信道中每个子载波中提取9个三阶累积量特征。为了降低计算工作量，只采用一根接收天线所接收到的数据，由于信道有30个子载波。因此提取出270个累积特征的特征向量。而图6中的等高线显示了不同动作的第一延迟量和第二延迟量之间估计的三阶累积量的二维等高线图。通过“坐下”、“刷牙”的图可发现其具有基本对称性。

图6 三阶累积量的2D等高线

2.3 特征筛选

本文中采用了基于互信息的特征筛选方法(MIFS)对原始特征进行筛选，并且设置β=0.75， 通过实验选择不同实验环境下筛选后的特征指数K(10、20、25、30、40维累积量特征)用于分类模型测试系统效果。

2.4 分 类

最终将得到的筛选后的特征子集输入到采用高斯核的经过粒子群算法优化过参数的支持向量机分类模型中进行分类，并且为了保证实验结果的精准性，采用10倍交叉验证来得出实验结果。

3 实验结果分析

实验所选的实验对象总共有10人。该10人含4名女6名男的本科生与研究生，年龄在19岁到25岁之间，身高在155 cm到183 cm之间，最终采集到实验室环境下2000个数据，会议室环境下3000个数据。并将其用于验证本方法的识别精度，最终得出表1与表2分别表示在不同场景下关于不同动作识别率的混淆矩阵，由表1看出实验室由于较为空旷受到的多径影响较小所以平均识别率达到97.4%，而会议室环境复杂，信号受到的多径影响较大但其平均识别率也达到了94.8%，而以上两种环境下本方法的平均识别率达到了96.1%。

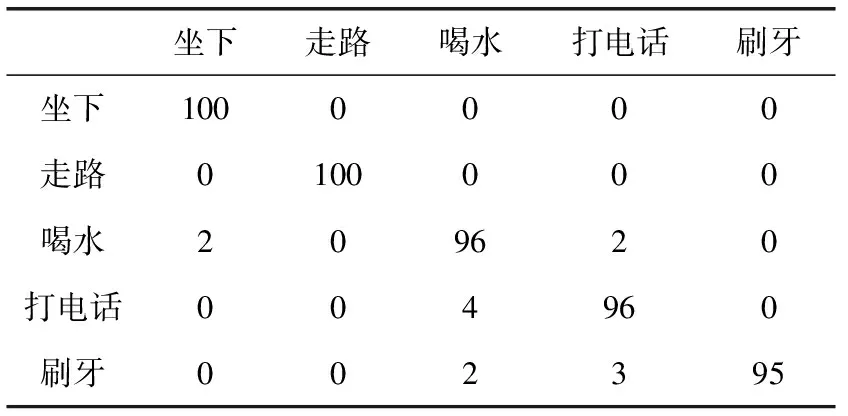
表1 实验室场景识别率/%

表2 会议室场景识别率/%

3.1 发包速率对识别率影响

为验证不同发包率对动作识别精度的影响，尝试了在不同的发包速率(50,100,200,500,1000) Hz下采集了不同人体日常行为的CSI原始数据，并采用10倍交叉验证，得出在不同速率下两种场景中的平均识别精度，由图7发包速率对识别率的影响图可以发现发包速率与实验的平均识别率成正比关系，但是当发包率到达500 Hz时，实验已经能取得较好的结果，而当发包率超过500 Hz时，准确率的提升并不明显，且越高的发包速率也带来了更高的丢包风险和计算时间。

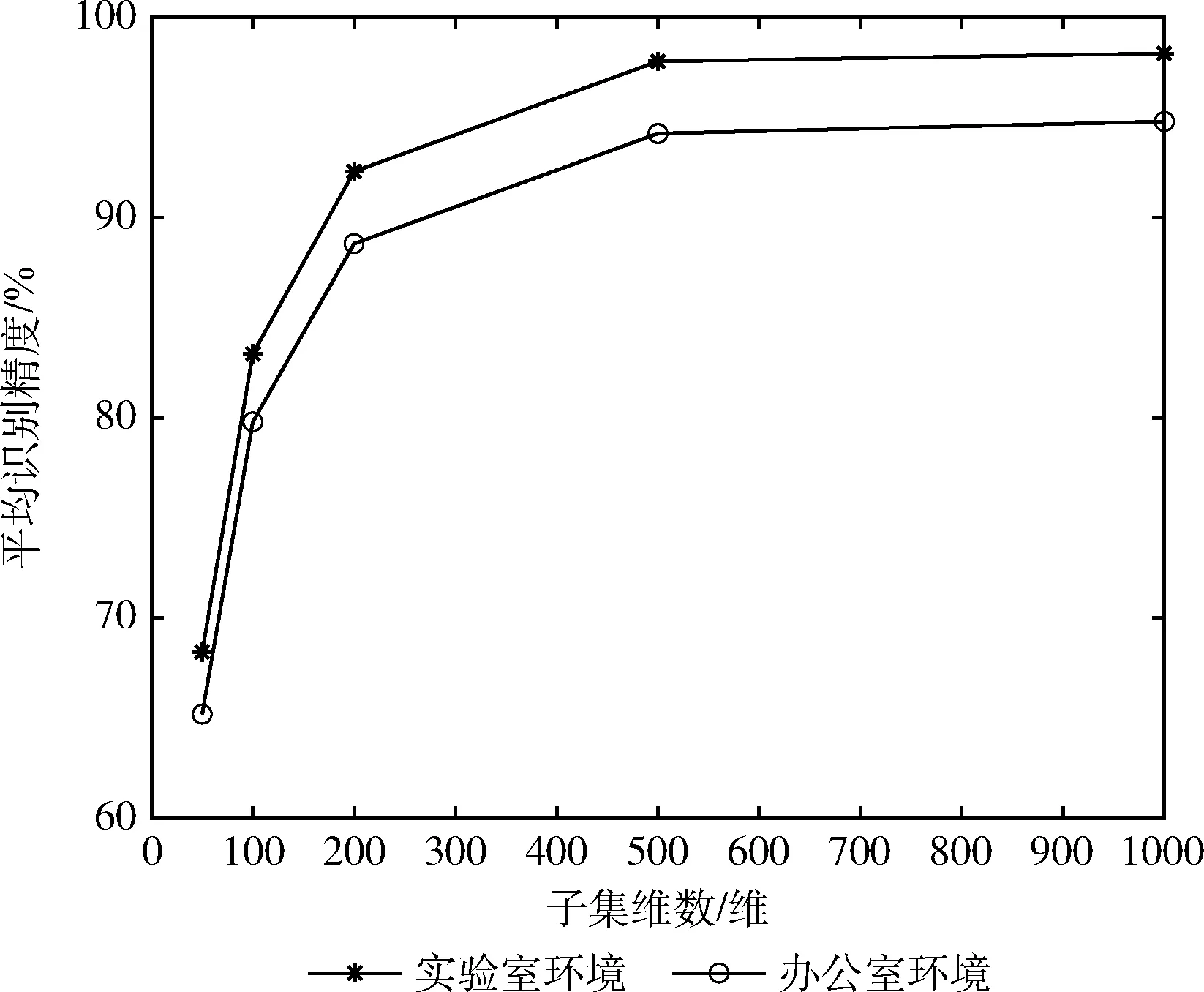
图7 发包速率影响

3.2 不同维度特征子集对识别率影响

为了验证不同维度的特征子集对识别率的影响，通过将提取到的原始特征向量，并通过MIFS降维算法将其降维成10、20、25、30、40维的特征子集，然后输入到优化好参数的SVM分类模型中，通过图8子集维度对识别率影响图可以发现，当K=30时，能获得较好的平均识别率，验证了当K=30时的特征子集已经能表达原信号绝大部分的信息，而当K超过30时对识别率的提升并不明显，而且更高的子集维度还会带来更大的冗余量和更高的过拟合风险。

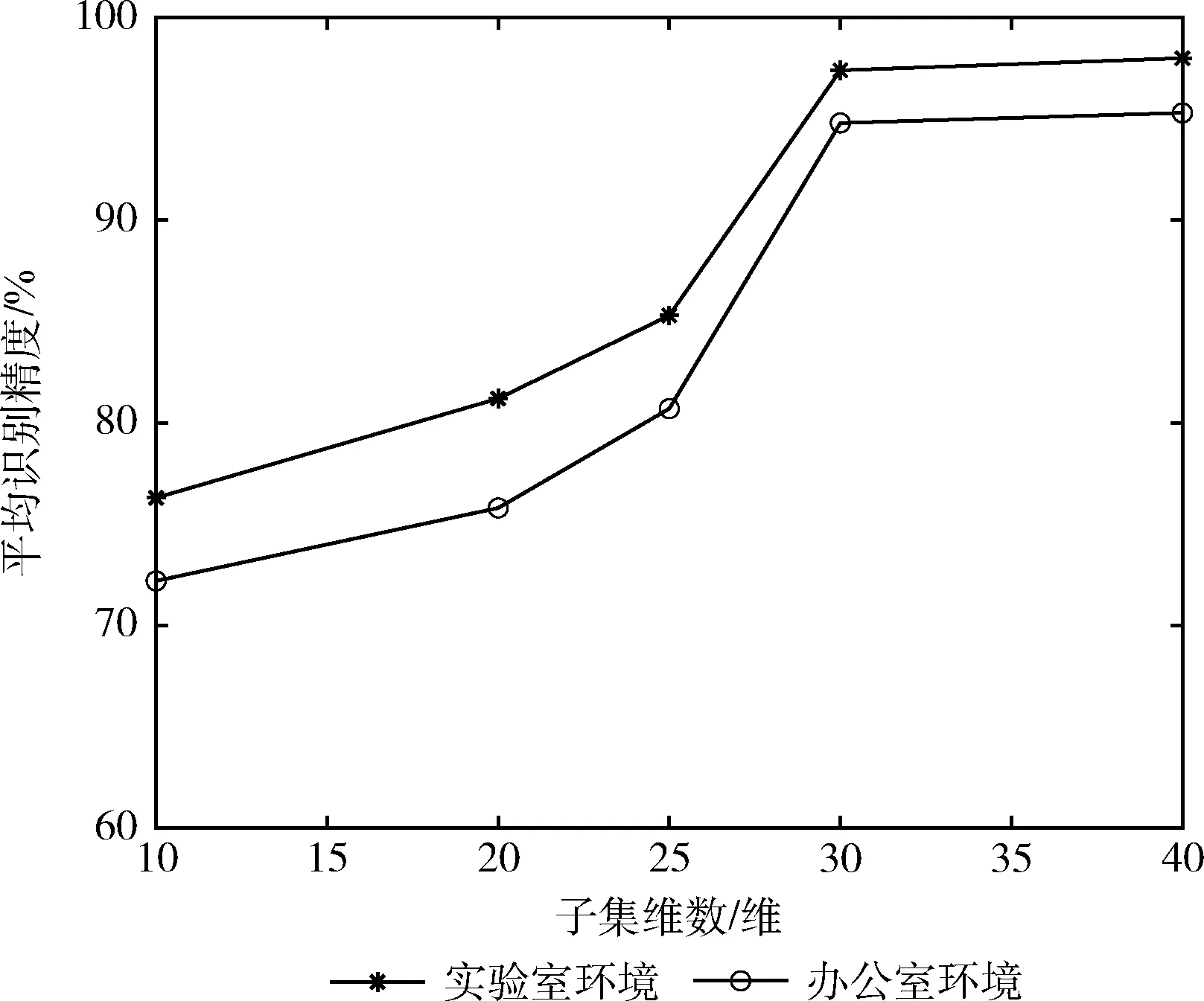
图8 子集维度影响

3.3 不同方法平均识别率对比

本文之前提及了3种现有的人体行为识别的方法，与其它方法相比，本方法省略了复杂的信号预处理阶段，但从表3可以看出本方法虽然降低了系统复杂度，但各动作的平均识别精度依然高于别的方法，可见本方法所提取的CSI信号的三阶累计量特征，保存了大部分原始信号的有用信息。对鲁棒性和识别精度的提升非常明显。

表3 各方法平均识别率对比

4 结束语

本文提出了一种基于信道状态信息的无设备的日常行为识别方法，首先通过两台连接上Intel 5300网卡的台式机做信号收发端采集原始CSI信号，随后在未进行去噪预处理的情况下提取信号的三阶累积量特征，再用基于互信息的特征选择方法构造出具有高鲁棒性的特征子集，最后将特征子集输入到经过了粒子群优化算法优化过参数的SVM分类器中进行分类。最终实现了不同场景下不同动作96.1%的平均识别率，验证该方法提取的三阶累积量作为特征在拥有较强鲁棒性的同时对提高识别精度有着显著作用。不过该方法目前仅实现了对单人单个动作的识别，且更换场景后还需要进行大量的训练，但鉴于现实生活需要，以后单人连续动作、多人多动作的识别以及跨场景动作识别将会是未来重要的研究方向。