小净距平行地铁隧道下卧土体长期沉降规律研究

刘羽航,徐国元,黎 伟

(华南理工大学土木与交通学院,广州 510641)

随着城市公共交通需求的增长，地铁成为各大城市的主要通行方式，地铁线路不断修建，同时因地质条件、地下空间规划的制约，致使新规划地铁线路与既有地铁隧道净距较小。目前，国内外学者对单线地铁隧道运营期沉降问题已进行较多研究，但针对小净距平行地铁隧道运营期沉降的研究相对较少，因此，分析小净距平行地铁隧道运营期沉降规律，对指导盾构地铁隧道施工及运营期的维护有重要指导意义。

赵春彦[1]认为，地铁隧道总的长期沉降可为附加静载引起的土体蠕变沉降及运营期列车循环荷载作用下的长期沉降之和，附加静载引起的土体蠕变沉降仅占总的长期沉降很小一部分，隧道运营期长期沉降是研究计算中的重点，目前，隧道运营期沉降的计算方法通常为以下3种。

(1)基于复杂土体动力本构关系建立三维仿真模型，并加载几十万次列车荷载，得出隧道长期沉降计算结果，但需要精确的数值建模及大量计算资源。

(2)基于大量隧道沉降监测数据，通过蚁群算法[2]及灰色理论[3]预测隧道运营期沉降，其预测精度较高，但人力物力成本较高，且在隧道结构施工前，甚至隧道施工阶段时，均不能对隧道长期沉降进行预测。

(3)结合室内土体动三轴实验，确定施加土体荷载次数-土体累计变形经验公式参数，建立列车荷载循环次数-隧道底部长期沉降的指数模型。其中，黄茂松[4]基于临界土力学，通过室内饱和软黏土循环荷载下总累积变形实验，建立了荷载循环次数-隧道总累计沉降模型；姚兆明[5]考虑土体受等压及偏压的影响，将土体围压归一化，同时考虑了土体主应力轴旋转的影响，进一步优化了黄茂松等[4]提出的列车循环荷载下隧道长期沉降模型参数；周建等[6]基于实验提出考虑土体先期固结情况及门槛循环应力的隧道运营期沉降预测模型；丁智等[7]探究了不同固结度饱和软黏土对隧道运营期沉降的影响；冯怀平等[8]探讨了不同饱和度对土体固结规律的影响；何绍衡等[9]通过海相软土动力试验，探究了时间间歇效应对土体动力特性的影响。

上述方法3中提到的经验公式法又分为两类：第一类CHAI[10]从土体应变状态出发，计算列车循环荷载作用下土体应变，进而建立反映基于应变的隧道长期沉降模型；第二类MONISMITH[11]从土体应力状态出发，计算列车循环荷载作用下土体应力，并计算土体动应力水平，进而建立反映动应力水平影响的隧道长期沉降计算模型。高广运[12]经过对比计算两类算法，得出基于应力状态计算得到的隧道长期沉降值较大，在实际工程上更趋于保守。

有关学者对上海地铁隧道沉降监测及土体实验做的比较完备[4-5，12]，因此以上海地铁1号线区段隧道为背景，采用第二类中地铁隧道运营期沉降预测模型[5]，运用ABAQUS软件建立有限元仿真模型，预测小净距平行隧道及对称轴处土体运营期沉降值，并分析运营速度及衬砌刚度对隧道沉降的影响规律。

1 建模参数及模型建立

1.1 模型本构及材料参数

上海市地铁1号线起始于上海新客站，向南延伸至萃庄，线路全长约13.5 km。隧道全线基本位于第④层淤泥质黏土中，隧道拱顶平均埋深10 m，采用预制钢筋混凝土装配式结构，通缝拼装，隧道外径6.2 m，内径5.5 m。

以上海地铁1号线人民广场站—新闸路区间单线隧道为工程背景，建立平行隧道仿真模型。考虑边界效应的影响，土体边界距隧道衬砌的距离均超隧道外径的5倍，故模型尺寸取X(150 m)×Y(120 m)×Z(80 m)，取隧道中心高程13.1 m，钢轨间距1.44 m[13-14]。模型中隧道衬砌、道床、轨道板及钢轨采用弹性本构，土体采用摩尔库伦本构。各结构接触及结构与土体接触采用绑定约束，隧道结构各材料参数见表1。隧道空间位置及典型断面工程土层分布情况如图1、图2所示。

表1 隧道结构材料参数

图1 隧道有限元模型

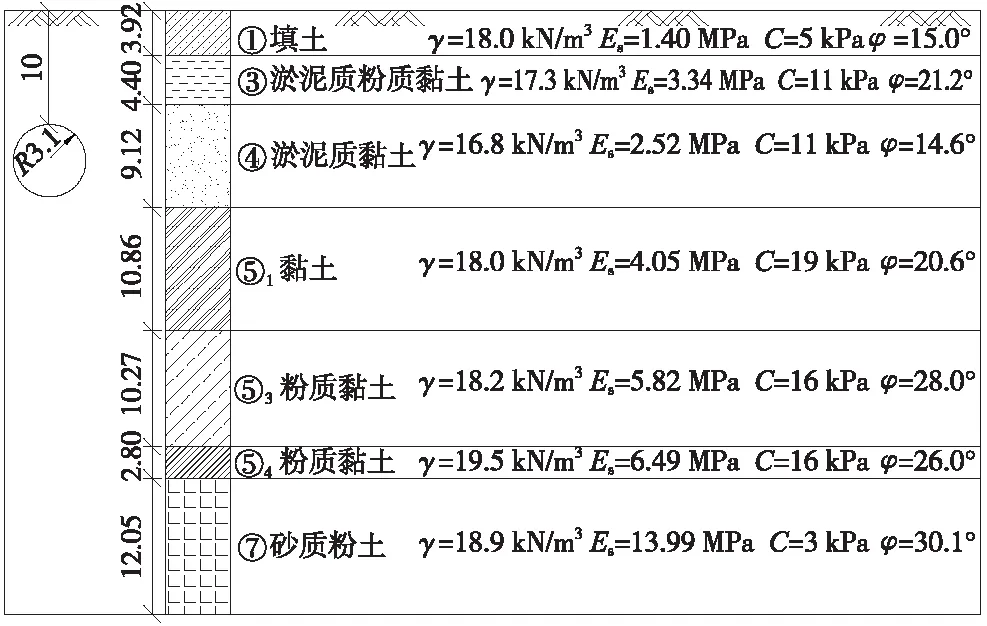
图2 典型区段断面土层分布(单位：m)

地铁运行过程为内源震动，且2个隧道共4个振动源，难以确定人工黏弹性边界中等效半径参数，故对于外行散射波，采用人工无限元边界优于人工黏弹性边界[15]。因此，在模型中两侧土体及底部土体均采用人工无限元边界，同时模型上表面不设约束。有限元模型细部如图3所示。

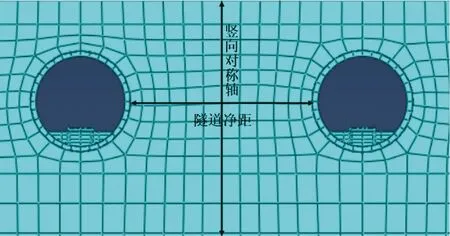
图3 隧道细部有限元模型

1.2 列车循环荷载的模拟

在地铁列车运行过程中，因轮轨不平顺[16]会产生竖向激振力及横向激振力，而和振兴[17]指出列车运行过程中产生的竖向激振力远大于横向激振力，在仿真模拟过程中，施加竖向激振力就能够满足仿真计算的精度要求，同时能简化模拟过程。参考英国铁路技术中心[18]对列车荷载的一系列研究，采用人工激励函数模拟列车运行过程中产生的激振力。

列车荷载人工激励函数为

F(t)=k[P0+P1sin(ω1t)+P2sin(ω2t)+

P3sin(ω3t)]

(1)

图4 列车单车轮荷载时程

以上述计算得到的激振力作为轮轨动力接触力输入值，利用VDLOAD子程序施加在轨道结构上，实现仿真模型中列车荷载的移动。

1.3 沉降计算模型

为反映等向、偏压固结不排水循环加载轴向塑性累积应变及超孔隙水压发展规律，基于塑性累积应变计算模型及不排水累积孔压模型，结合分层总和法，将饱和软黏土地基总累积沉降分为不排水循环累积变形引起的沉降与不排水循环累积孔压消散引起的固结沉降两部分计算。计算超孔隙水压力时，采用一维太沙基固结方程求解，长期来看，可认为超孔隙水压完全消散，因此，取固结度为100%，计算结果更趋于保守。

不排水循环累积变形计算模型为

(2)

不排水循环累积孔压计算模型为

(3)

结合式(2)与式(3)，分别求得土体不排水循环累积变形引起的沉降及土体不排水循环累积孔压消散引起的固结沉降，二者求和即得到隧道处及对称轴处土体运营期沉降。

2 仿真模型验证

提取施加单辆列车循环荷载过程中，隧道道床水平加速度时程曲线及距隧道底正下方1 m处土体动应力时程曲线，分别如图5、图6所示。

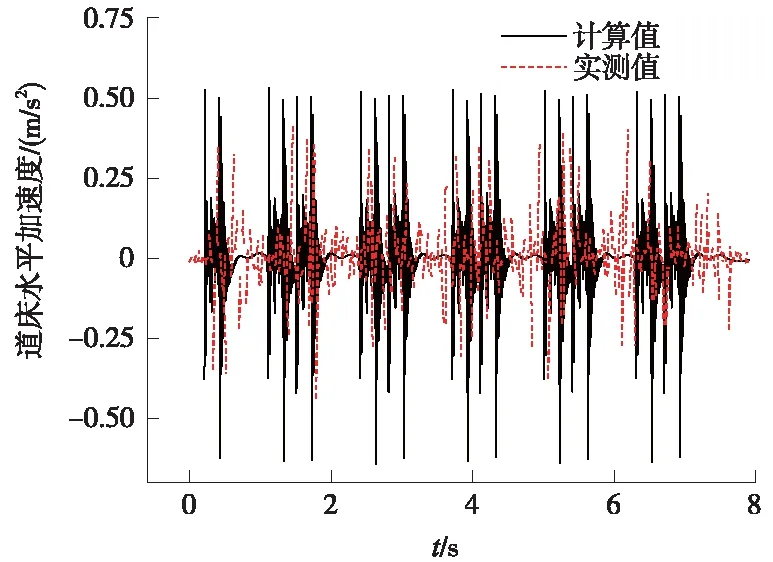
图5 隧道道床水平加速度时程曲线

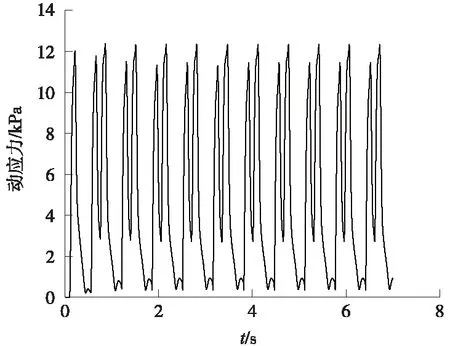
图6 距隧道底1 m处土体动应力时程曲线

仿真计算得到的隧道道床加速度及土体动应力均出现12个峰值，对应上海1号线列车12个转向架处轮轨运行中荷载循环过程，道床水平峰值约为0.5 m/s2，隧道底正下方1 m处土体动应力峰值约为12 kPa，南京地铁列车[19]与上海地铁1号线均为国产A型列车，其运行时隧道道床水平加速度实测峰值约为0.38 m/s2，土体动应力最大值约为10 kPa，本次仿真计算中隧道道床水平加速度与南京地铁运营时实测数据变化趋势一致，数值接近。

取地铁列车车速为72 km/h，按地铁列车每年运行20万次计算隧道运营期沉降。计算动应力水平及土体孔压值时，采用单层土中心应力代表该层土体应力状态。从保守角度考虑，即认为孔压完全消散，则可得单辆地铁列车运营20年内，隧道运营期沉降，如图7所示。

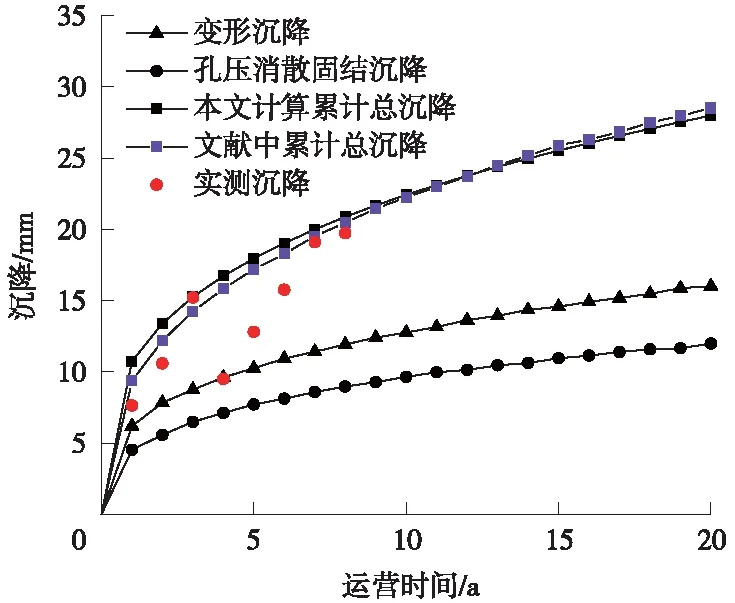
图7 隧道沉降随运营时间变化曲线

在运营时间达到1，2，5，10，20年后，隧道累计沉降值分别为10.73，13.39，17.95，22.41，27.98 mm，高广运[12]文中计算得到的相应运营时间对应累计沉降为9.35，12.18，17.1，22.1，28.87 mm，本文计算得到的隧道运营期沉降值与其计算得到的隧道运营期沉降值及沉降变化趋势近似一致，也与地铁1号线人民广场站—新闸路站区间隧道实测累计沉降值[20]及累计沉降增长趋势较为一致。

上海地铁隧道多处于砂、粉性土层及软土层，埋深10～40 m，不同线路所处的工程环境因隧道渗漏水，外部工程施工等众多因素影响而各异，隧道平均长期沉降从20～200 mm皆有分布，但隧道长期沉降规律较为一致，均随时间变化呈指数增长，部分隧道累计沉降值如图8所示[20-23]。

图8 上海部分地铁线路累计沉降曲线

由图8可知，隧道长期沉降随时间增加而近似呈指数增长，同时增长速率逐年减小。隧道沉降拟合结果及相关性见表2。其中，Y为隧道沉降，t为时间(以月计)。

表2 隧道沉降拟合结果

3 平行隧道沉降计算结果分析

目前，对小净距地铁隧道暂无明确定义，借鉴JTG 3370.1—2018《公路隧道设计规范》中根据不同围岩等级，以净距小于隧道开挖断面宽度一定倍数的分离式独立双洞隧道为小净距隧道的方法，上海地铁1号线地铁隧道所处地层多为软黏土，地质条件较差，因而围岩等级取Ⅵ，可认为当平行隧道净距小于4倍隧道直径时，为小净距工况。

城市地铁隧道建设时，邻近2条地铁盾构隧道管片的净距一般大于2 m，因而在数值模拟中以0.3D(D为盾构隧道外径值)即1.86 m，作为选取的最小净距，取4.2D为平行隧道模拟选取的最大净距。净距每隔0.3D计算一次，分别建立净距为0.3D～4.2D等14个仿真模型。按最不利工况即列车交汇运营工况，计算隧道运营期总沉降值及模型对称轴线处土体运营期总沉降值，结果如图9、图10所示，同时可得运营20年时，隧道及对称轴处土体沉降随隧道间净距变化情况，如图11所示。

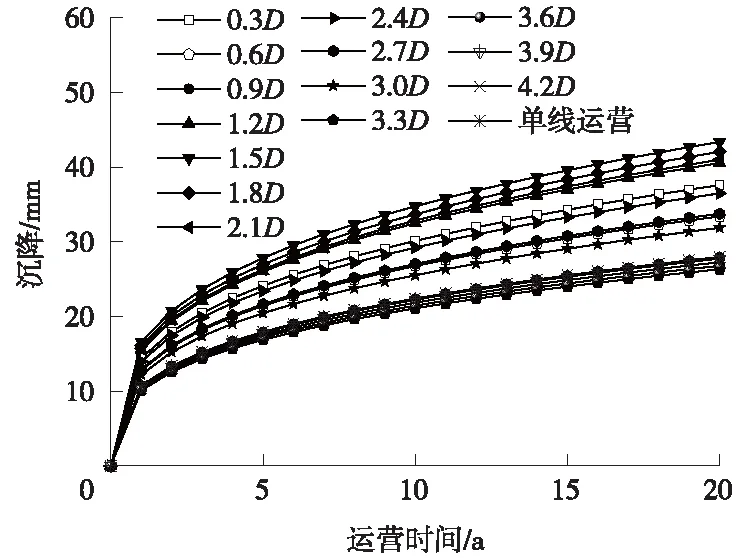
图9 不同净距隧道总沉降随运营时间变化

图10 不同净距轴线处总沉降随运营时间变化

图11 运营20年时隧道及轴线处沉降随净距变化

3.1 隧道总累计沉降分析

首先，对交汇运营工况隧道总累计沉降进行分析，由图9可知，当地铁列车交汇运营时，隧道总累计沉降随时间增长规律与单线运营时一致，隧道总累计沉降均随运营时间的增加而呈指数增大趋势，并且在运营到第10年时，隧道总累计沉降完成超过最终沉降的80%；地铁列车交汇运营到第20年时，隧道总累计沉降该年内增长不到1 mm，可认为隧道沉降已经完成。隧道总累计沉降并非简单地随着隧道间净距的增大而减小，而是随着隧道间净距的不同呈现不同的规律。

由图9及图11可知，当平行隧道间净距为0.3D～0.9D时，隧道总累计沉降分别为37.60，33.41，28.01 mm，随着净距的增大，隧道总累计沉降逐渐减小，但仍大于单线运营时隧道总累计沉降；当平行隧道间净距为1.2D～1.5D时，隧道总累计沉降分别为40.56，43.39 mm，隧道总累计沉降较大；当平行隧道间净距为1.8D～3.0D时，随着平行隧道间净距的增大，隧道总累计沉降总体呈减小趋势；当平行隧道间净距为3.3D～4.2D时，隧道总累计沉降变化幅度很小，且逐渐逼近地铁单线运营时隧道总累计沉降，此时平行隧道间净距的变化对隧道总累计沉降影响不大，表明净距超过3.3D后，隧道总累计沉降几乎不受交汇运营工况的影响。

当平行隧道间净距为0.3D～0.9D时，交汇运营时列车循环荷载产生对称的双重应力波，土体应力波相互叠加，致使土体的塑性累计变形及土体内超孔隙水压力较单线运营时进一步增加，因而隧道总累计沉降大于单线运营时的隧道总累计沉降；当隧道间净距为1.5D时，隧道总累计沉降达到最大值43.39 mm，相较于净距为0.9D时的隧道总累计沉降值28.01 mm，增长了近50%，表明距离隧道为0.9D～1.5D处的土体响应变化剧烈；当平行隧道间净距为1.2D～3.0D时，隧道总累计沉降大于净距为0.9D时的隧道总累计沉降。这是由于隧道正下方土体不仅受到本隧道上方列车循环荷载的动力作用，同时恰好处于另一条隧道内列车循环荷载导致的土体振动放大效应区内，此隧道正下方的土体所受动力进一步增大，导致隧道总累计沉降进一步增大。通过计算可知，距离隧道1.2D～3D处的土体，其响应出现振动放大，与高广运[24]提出的距离隧道1D～3D时出现此种效应几乎一致。

3.2 对称轴线处土体总累计沉降分析

对模型对称轴线处土体总累计沉降进行讨论分析，由图10及图11可知，平行隧道地铁列车交汇运营工况下，平行隧道间净距相同时，轴线处总累计沉降小于隧道总累计沉降。轴线处总累计沉降随运营时间增长规律与隧道总累计沉降随运营时间发展规律一致，故不予赘述。轴线处总累计沉降随平行隧道间净距变化规律与隧道总累计沉降随平行隧道间净距变化规律并不相同，随着平行隧道间净距的增大，轴线处总累计沉降随净距增加近似呈指数减小趋势。

当隧道间净距为0.3D时，轴线处总累计沉降为最大值，其值为32.87 mm，仅此净距时大于单线地铁运营时隧道总累计沉降。当平行隧道净距为3.9D、4.2D时，轴线处总累计沉降分别为4.30，2.38 mm，此时净距增大1.86 m而轴线处总累计沉降仅减小1.82 mm。可以认为，隧道净距>4D后，轴线处总累计沉降变化较小，且其值趋近于零。轴线处于不同净距的位置时其沉降均小于隧道处总沉降，说明隧道处总沉降为空间上土体沉降最大处。

轴线处土体并未出现振动放大效应，这是由于在对称轴位置处，对称波源产生的对称应力波部分相互抵消，导致土体实际所受应力减小，进而土体塑性累计沉降及固结累计沉降也相应减小，最终致使该处土体总累计沉降减少。从上文的振动放大效应的角度来看，可将2条隧道及周围土体视作一个整体的“大隧道”，此时其轴线处土体并未处于振动放大区，因此沉降值不大。

3.3 平行隧道下卧土体长期沉降函数

以上文计算得到的单线运营时隧道总累计沉降值作为基准值，考虑平行隧道间净距带来的影响，提出分别建立适用于软土地区净距>0.3D的平行隧道总累计沉降函数

(5)

以及对称轴线处土体长期沉降函数如

(6)

式(5)及式(6)中，Ss、Spu、Spm分别为运营至某年时，单线隧道总沉降值，双线隧道总累计沉降，双线隧道对称轴线处土体总累计沉降；s为隧道间净距倍数。

3.4 其他因素对平行隧道沉降的影响

取隧道间净距为1.8D作为基准工况，计算分析列车速度及衬砌刚度对沉降的影响，计算结果如图12及图13所示。

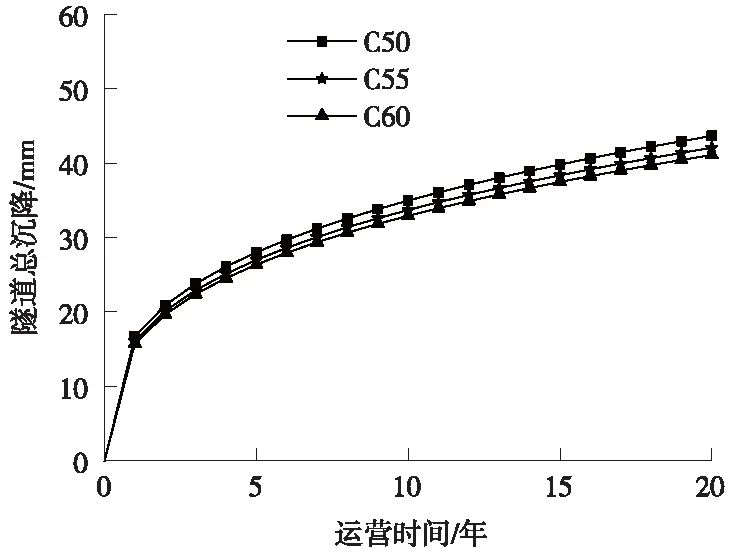
图12 不同衬砌刚度隧道沉降随运营时间变化

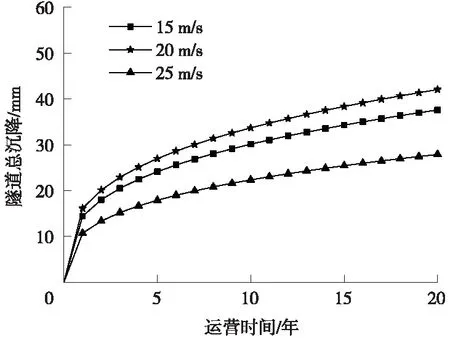
图13 不同列车速度隧道沉降随运营时间变化

从图12可以看出，列车速度越大，隧道沉降越小，列车速度的影响较大，这是因为速度增大后，列车荷载虽然增大，但其作用时间较短，土体所受动应力较小，因而对土体扰动更小[25]。

隧道刚度越大，隧道沉降越小，但刚度对沉降影响较小。在实际工程中增大管片刚度对沉降影响不大，可考虑在软弱地基区段内提高列车运行速度，减少隧道沉降。

综合考虑上述因素，在实际工程中，为减小平行隧道长期沉降，设计上尽可能避免使隧道净距为0.3D～1.8D，有条件时尽量使隧道净距大于3D，不能满足时，可考虑对隧道土体进行加固处理，转换软土性质，减小土体循环累计沉降值；运营时可提高列车运营速度，减少对土体的扰动。另外对软弱路基段，车站与隧道过渡段，也应进行加固处理，避免产生较大的差异沉降。

4 结论

(1)平行隧道下卧土体运营期总累计沉降增长规律与单线隧道下卧土体运营期总累计沉降增长规律一致，隧道累计沉降均随列车运营时间增长而呈指数增大，超过20年后沉降基本稳定。

(2)平行隧道长期沉降随净距增加呈不同规律。随着净距的增加，隧道运营期总累计沉降先减小再增大，最后减小至趋于单线运营时沉降，净距为1.2D～1.8D时，隧道总累计沉降有最大值；模型对称轴线处土体的总累计沉降随净距的增大近似呈指数减小。

(3)列车运行速度、衬砌刚度与土体沉降正相关。列车运行速度越快，土体沉降越小；隧道刚度越大，土体沉降越小。

(4)相较于衬砌刚度，隧道净距、运行速度对土体沉降的影响更大。在实际工程中，增大隧道间净距、提高列车运行速度、加固隧道周围土体，可有效降低隧道长期沉降，并减小隧道变形，维护列车安全运行。