温度梯度作用下既有离缝无砟轨道结构层间损伤扩展及变形分析

林士财

(1.中铁第一勘察设计院集团有限公司,西安 710043； 2.陕西省铁道及地下交通工程重点实验室(中铁一院),西安 710043)

CRTSⅡ型板式无砟轨道结构作为纵连结构，与无缝线路相似，轨道结构的稳定性对温度荷载较为敏感。轨道板内正温度梯度、负温度梯度荷载的周期性循环作用，导致轨道板与砂浆层之间的黏结力逐渐失效，进一步放大温度荷载的作用效果，从而导致轨道板底部形成离缝，离缝区域扩展及持续性增大诱发轨道板上拱，极易引起轨道板高温环境下失稳[1-3]。

国内外诸多学者对轨道板离缝及上拱问题进行了大量研究。朱永见等[4]研究了CRTSⅡ型板式无砟轨道层间离缝产生的原因，并推导了离缝产生的临界温度；刘浩等[5]分析了纵连式无砟轨道端刺区轨道结构的稳定性；刘付山等[6]研究了施工过程中CRTSⅡ型板式无砟轨道的上拱特性；刘笑凯等[7-10]推导出温度荷载作用下，轨道板上拱波形表达式，从而得到了上拱矢度与波长的对应关系；陈龙等[11]分析了推板条件下轨道板与砂浆层之间的传递规律，探讨了不同滑移参数对层间应力的影响；赵春发等[12]在内聚力模型的基础上，分析了循环温度荷载对不同黏结状况下的层间伤损扩展规律；ZHONG Y等[13-14]分析了温度梯度作用下，未纵连的CRTSⅡ型板式无砟轨道的变形与界面应力，研究了界面损伤演化规律和疲劳性能；冯青松等[15]研究了不同CA砂浆离缝位置对轨道几何形位及对无缝线路受力变形的影响；张向民等[16]确定了CRTSⅡ型板式无砟轨道上拱变形的全过程平衡路径及临界失稳条件；高亮等[17]分析了不同层间黏结状态与不同板间接缝状态下轨道板的上拱变形。

现有研究多考虑温度荷载作用下纵连板式无砟轨道稳定性及层间界面损伤的发展规律，鲜见分析温度荷载对既有离缝无砟轨道结构的影响。为此，基于有限单元法及界面损伤内聚力模型，建立路基上既有离缝无砟轨道有限元分析模型，旨在探讨温度荷载作用下既有离缝无砟轨道结构受力、变形发展规律和界面损伤扩展机制，以期为高速铁路养护维修提供理论参考。

1 板式无砟轨道-路基有限元模型

1.1 有限元模型建立

路基上CRTSⅡ型板式无砟轨道主要由钢轨、扣件系统、轨道板、砂浆层和底座板等组成。钢轨类型选取为我国高速铁路采用的标准60 kg/m型钢轨，以空间点支承梁进行模拟，弹性模量E=210 GPa；以连接器单元来模拟扣件的支承和约束作用，扣件横向、纵向和竖向刚度分别为60，50，60 kN/mm；轨道板、砂浆层、底座板和路基均采用实体单元模拟。所建立的有限元模型如图1所示。各结构层材料参数见表1。

图1 CRTSⅡ型板式无砟轨道有限元分析模型

表1 板式无砟轨道各结构层材料参数

1.2 内聚力模型

内聚力模型是将复杂的破坏过程用两个面之间的“相对分离位移-力”关系表达的一种宏观物理概念，能较好地描述界面损伤规律和破坏机理。采用双线性“张力-位移”关系模拟层间黏结作用，如图2所示。

图2 双线性“张力-位移”关系

双线性内聚力模型“张力-位移”关系表达式如下

(1)

临界断裂能公式如下

(2)

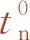
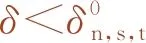
损伤萌生判定准则采用二次名义应力准则，如式(3)所示，而界面损伤演法采用能量准则。

(3)

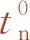
1.3 模型及工况说明

受太阳辐射强度、气温及风速等因素影响，轨道板上、下表面产生温差(即温度梯度)。现有研究表明，温度梯度为复杂随机变量，但随着轨道结构深度增加波动逐渐减小，当深度达到轨道板厚度(0.20 m)时已基本趋于稳定。为此，温度梯度荷载仅施加于轨道板。

为分析不同温度梯度对界面损伤和离缝发展的影响，同时考虑极端温度荷载，本文正温度梯度取值从0 ℃/m增长至100 ℃/m，负温度梯度取值从0 ℃/m降低至-80 ℃/m。

荷载施加的方法如下：

(1)施加轨道板、砂浆层和底座板重力荷载；

(2)初始化温度荷载；

(3)施加温度荷载；

(4)扣除初始重力效应，得到温度和重力共同作用下轨道板受力及变形特性。

1.4 采样节点说明

图3为轨道板各采样节点的相对位置，以此准确反映层间界面损伤发展趋势，共设13个采样节点，节点1位于轨道板正中心，节点2位于轨道板离缝横向中心线边缘，节点3位于离缝边缘线中心，节点4位于离缝边缘线板边。既有离缝长度取一块板长，即l0=6.50 m。

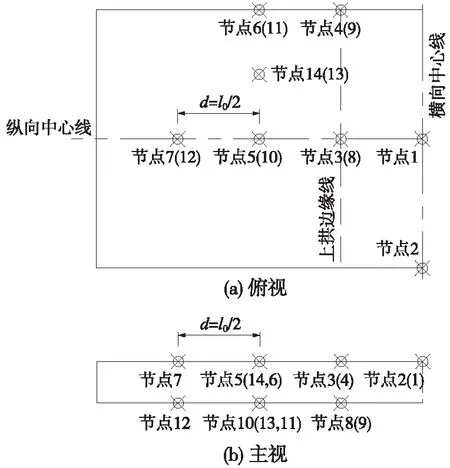
图3 各采样节点的相对位置

2 界面损伤与离缝扩展分析

2.1 正温度梯度作用

图4、图5列举了正温度梯度荷载作用下，轨道板各采样节点损伤因子随温度梯度变化曲线及界面损伤云图。

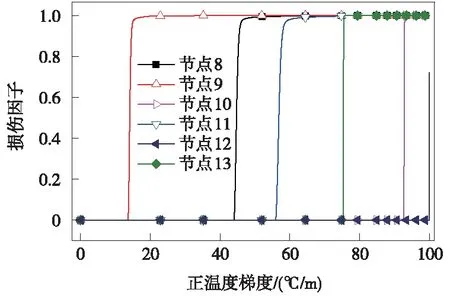
图4 各采样节点正温度梯度-损伤因子曲线

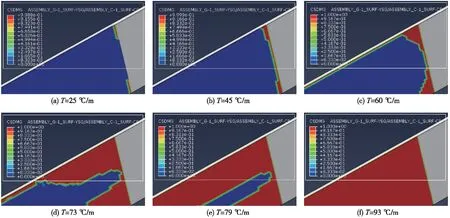
图5 正温度梯度作用下的界面损伤云图

由图4、图5可以得到以下规律。

(1)各采样节点的损伤因子随温度梯度的增大表现出相似的变化趋势，损伤因子均由0逐渐增大至1，即轨道板与砂浆层间黏结逐渐失效。

(2)层间损伤萌生所对应的温度梯度存在明显差异，板角位置(节点9)最先形成损伤，所对应的损伤正温度梯度为13.64 ℃/m；离缝边缘(节点8)及板边(节点11)损伤相对滞后。

结合界面损伤云图总结界面损伤萌生及发展示意如图6所示。可见，正温度梯度作用下界面损伤主要表现如下。

图6 伤损萌生及发展示意

(1)轨道板与砂浆层间损伤萌生于离缝板角处，即DS位置，且随着正温度梯度的增大，界面损伤逐渐扩展。原因在于离缝区层间连接薄弱，正温度梯度作用下离缝区自由变形导致板角位置处界面内应力过大，超过界面黏结强度所致。

(2)随着正温度梯度的增加，界面损伤由萌生位置沿上拱边缘线和轨道板板边线呈直角形扩展，表现为明显的斜向撕裂特征。

(3)纵向中心线两侧一定宽度(Ⅳ位置)界面损伤滞后明显，其余位置界面黏结均已失效，如图5(e)所示；但随着正温度梯度的逐渐增大，Ⅳ位置处损伤区域逐步扩大，且从中心向端部传递，最终将导致整板脱黏，如图5(f)所示。

界面损伤扩展势必导致轨道结构空间几何状态发生改变，换言之，轨道结构位移变化一定程度上亦能反映出界面损伤的发展规律。图7给出了初始离缝长度为6.5 m时，正温度梯度作用下轨道板各采样节点的竖向、横向位移随温度梯度变化曲线，可以得到以下规律。

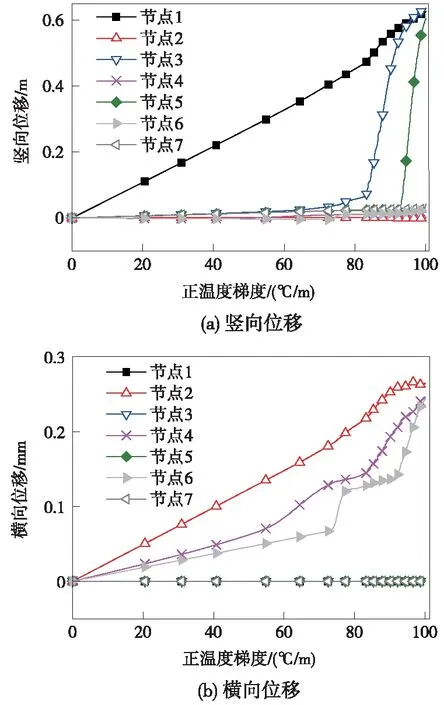
图7 轨道板节点位移-正温度梯度变化曲线

(1)既有离缝区内节点1，轨道板竖向位移随正温度梯度的增大逐渐增大，并存在转折点，温度梯度为100 ℃/m时，轨道板竖向位移为0.63 mm；离缝区板边节点2的竖向位移基本为0。

(2)黏结区内板边节点4和节点6的竖向位移基本为0；而节点3和节点5的竖向位移随正温度梯度的增加，起初呈缓慢增加的变化趋势，而后出现明显突变，增长速度加快。主要原因在于轨道板横向贯通脱黏所致。

(3)板中节点1、3、5、7横向位移无明显变化；板边节点2、4、6的横向位移随正温度梯度的增大逐渐增大。

2.2 负温度梯度作用

图8、图9列举了负温度梯度荷载作用下，轨道板各采样节点损伤因子随温度梯度变化曲线及界面损伤云图。由图8、图9可以得到以下规律。

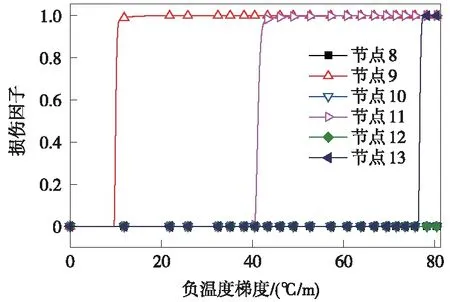
图8 各采样节点正温度梯度-损伤因子曲线

图9 负温度梯度作用下的界面损伤云图

(1)与正温度梯度荷载作用相似，各采样节点的损伤因子随温度梯度的增大表现出相似的变化趋势，损伤因子均由0逐渐增大至1。

(2)层间损伤萌生所对应的温度梯度存在明显差异。板角位置(节点9)最先形成损伤，所对应的损伤负温度梯度为-9.56 ℃/m；离缝边缘(节点11)及板边(节点13)损伤相对滞后，其余节点未表现损伤。负温度梯度荷载作用下，界面损伤发展趋势与前述发展趋势相似，板角仍是界面损伤萌生位置；随着负温度梯度的持续增大，界面损伤由板角逐渐向板中发展；负温度梯度达-80 ℃/m时，轨道板与砂浆层间仍存在未脱黏纵向区域。

图10给出了初始离缝长度为6.5 m时，负温度梯度作用下轨道板各采样节点的竖向、横向位移随温度梯度变化曲线，可以得到以下规律。

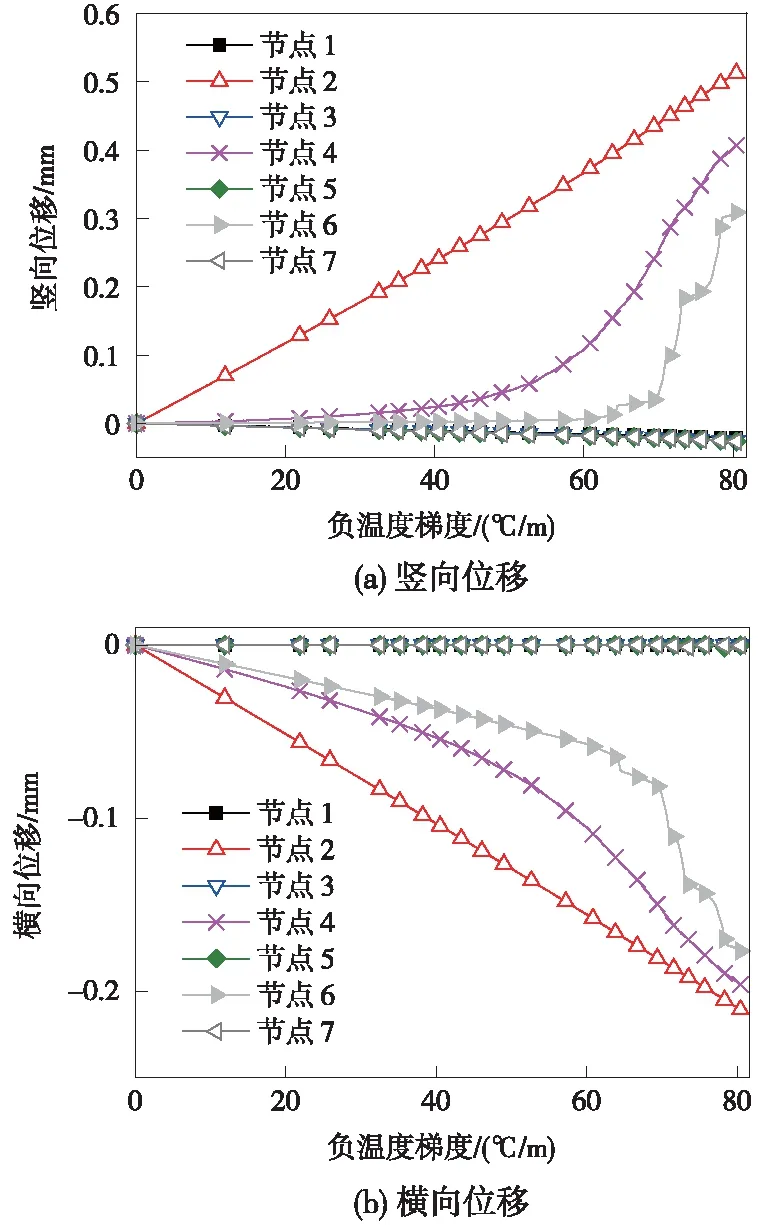
图10 各采样节点负温度梯度-损伤因子曲线

(1)随负温度梯度增加，板中节点1、3、5、7竖向位移有轻微下降趋势，但量值基本保持在0 mm左右，这从变形角度侧面论证了轨道板中部未脱黏，轨道板与砂浆层仍具有可靠黏结。

(2)离缝区板边节点2的竖向位移随负温度梯度的增大呈线性增大，原因在于其竖向无约束；而黏结区板边节点4、6的竖向位移随负温度梯度的增大呈现明显的非线性增长趋势，界面黏结力破坏后，增长速度逐渐加快。

(3)纵向中心线上的节点1、3、5、7，横向位移无明显变化；板边节点2、4、6的横向位移随负温度梯度的增大逐渐增大。

综上分析，总结如下。

(1)既有离缝无砟轨道在梯度荷载作用下，轨道板在空间上表现为“板中上拱，四角下沉，横向鼓胀”(正温度梯度)和“板中下凹，四角上翘，横向缩进”(负温度梯度)的变形特点。

(2)黏结区轨道板与砂浆层间的黏结一旦破坏，温度梯度荷载作用下，轨道板与砂浆层间的离缝长度逐渐扩展，黏结区损伤横向贯通后，轨道板竖向位移存在明显突变。

(3)正、负温度梯度作用下，损伤均萌生于离缝区与黏结区衔接处板角位置，并随温度梯度的增加呈斜向发展趋势。

(4)温度梯度较大时，轨道板中部仍存在部分黏结区，且正温度梯度作用下层间损伤发展速度明显高于负温度梯度作用。

3 轨道板上拱对结构受力的影响

如前文所述，温度梯度荷载作用加剧既有离缝扩展，而轨道板与砂浆层间离缝是诱发纵连轨道板上拱的主要因素之一。

上拱区域由于轨道板与砂浆层黏结力损失，二者之间设置为摩擦约束，而上拱区域两侧轨道板与砂浆层界面黏结良好，考虑二者之间的黏结强度。以单波余弦型曲线描述轨道板的上拱波形曲线，其表达式如下

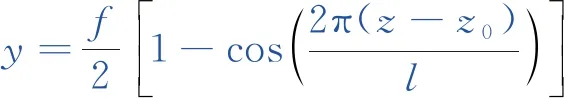
(4)

式中，l为轨道板初始波长；z0为上拱起始位置；z为上拱发生位置；f为轨道板上拱幅值。

上拱波长取值从6.5 m变化至39 m，增幅6.5 m，上拱幅值为5，10，15，20 mm，共计24种工况。

当l≤19.5 m时，上拱端部轨道板与砂浆层间形成一定损伤，表2罗列了不同上拱波长和上拱幅值条件下的损伤情况，表中，Dmax为损伤因子最大值。可以得到以下规律。

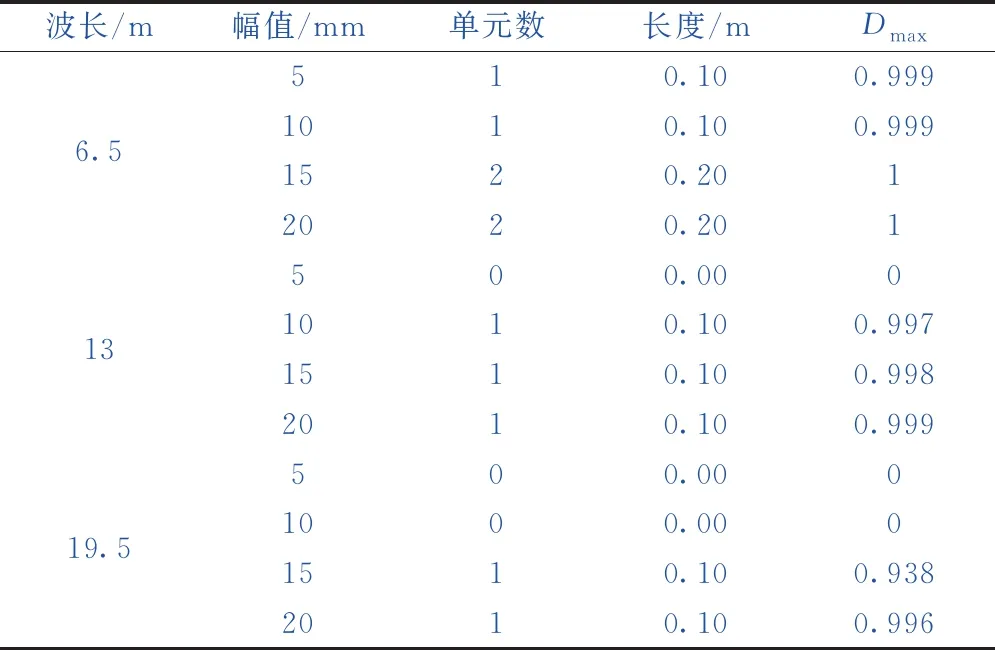
表2 伤损情况统计

(1)轨道板上拱对其端部0.1～0.2 m内界面黏结强度存在不利影响，当Dmax=1时，表明界面黏结已完全失效。

(2)上拱波长一定时，随上拱幅值的增加，损伤因子逐渐增大；上拱幅值一定时，随上拱波长的增加，损伤因子逐渐减小。

图11为上拱形式为10 mm/19.5 m时，轨道板上表面中线和下表面中线的纵向应力分布曲线。可以得到以下规律。

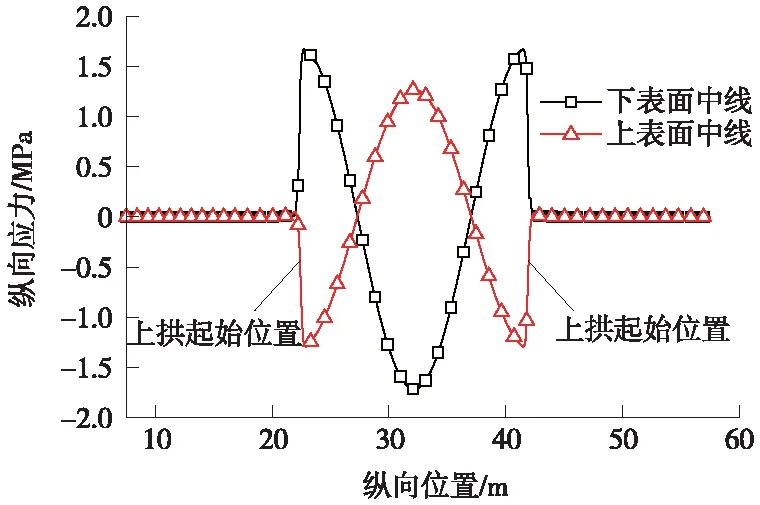
图11 轨道板上、下表面中线的纵向应力分布曲线

(1)轨道板的纵向应力分布具有明显的规律性。主要表现为：由端部向上拱幅值处过渡，轨道板上表面的纵向应力由零应力状态逐渐转为受压状态，而后逐渐转为受拉状态；下表面的纵向应力分布则相反。

(2)轨道板上拱发生后，轨道板的纵向最大拉应力位置主要有两处，其一是上拱幅值所对应的轨道板上表面位置，其二是上拱端部所对应的轨道板下表面位置；而纵向压应力则相反，最大拉应力位置处的相对位置产生最大压应力。

表3统计了24种工况条件下，轨道板上、下表面的纵向最大拉应力，可以得到以下规律。

表3 纵向应力与幅值和波长的对应关系 MPa

(1)上拱波长恒定时，轨道板的上表面、下表面的纵向最大拉应力随上拱幅值的增大而线性增大。

(2)上拱幅值恒定时，轨道板纵向最大拉应力随着波长的增加逐渐减小，随上拱波长增加，轨道板纵向最大拉应力由轨道板上表面转移至下表面。

(3)上拱幅值的增加明显加剧了轨道板的纵向应力水平，混凝土开裂风险加大，尤其在波长较小时，其影响极为显著；上拱波长的增加可减缓轨道板的纵向应力水平，降低混凝土开裂概率。

4 结论

(1)初步揭示了温度梯度荷载作用下既有离缝无砟轨道层间损伤发展、变形规律及不同上拱条件下轨道板的受力特性。

(2)温度梯度荷载作用下，层间损伤萌生于离缝区与黏结区衔接处板角位置，并随温度梯度的持续增大斜向发展；轨道板中部存在明显黏结区。

(3)与负温度梯度荷载作用相比，正温度梯度荷载作用下，轨道板底部更易发生整板离缝脱黏。

(4)轨道板上拱导致端部0.1～0.2 m存在明显黏结弱化区。

(5)小波长、大幅值形式的轨道板上拱更易引起轨道板开裂。