高速铁路三维轮轨瞬态滚动接触-冲击模型参数研究

王攀杰,刘建利,李 博,,安博洋

(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031； 2.西南交通大学土木工程学院,成都 610031； 3.西安市轨道交通集团有限公司,西安 710000)

车轮在钢轨上的滚动接触是解决许多轮轨相关问题的关键，如磨损、塑性变形、滚动接触疲劳(RCF)、车辆动力学和车辆-轨道相互作用。然而，目前缺乏精确测量滚动接触问题(如接触应力和应变状态)的实验方法，特别是在动态条件下[1]。因此，重点应放在分析和基于计算机的数值模拟方法上。

轮轨接触研究始于19世纪，HERTZ[2]是最早用半空间假设提供弹性体之间无摩擦法向接触解析解的研究者之一；MINDLIN[3]发展了赫兹接触理论，推导出竖向或水平向荷载作用在半无限弹性体内部时体内任一点的应力与应变的数学解，从而来处理在摩擦极限内切向力引起的接触体位移；CARTER[4]对轮轨摩擦滚动接触进行了研究，利用二维分析模型计算了滚动方向上的黏着蠕滑现象；VERMEULEN和JOHNSON[5]通过假设一个椭圆的黏着面积，将CARTER的二维理论扩展到了具有纯蠕变和无旋转的三维理论；KALKER[6]用级数方法讨论了具有椭圆形接触区的三维滚动接触问题，先后提出的线性理论、精确理论和简化理论，是目前最广为接受的计算方法，其相应的数值程序FASTSIM和CONTACT至今广泛应用于车辆动力学和滚动接触力学的求解。

近年来，随着铁路网运行速度、轴重和交通密度的不断提高，轮轨滚动接触的研究越来越受到重视，但经典的接触力学理论由于本身存在的假设与局限性，已经难以满足铁路发展的需要。随着计算机性能的发展，利用显式时间积分方法进行瞬态有限元模拟，不仅可以考虑真实接触几何，也可考虑材料的非线性行为，使得有限元法更适合解决接触条件和材料特性复杂度高的轮轨滚动问题。

许多学者利用有限元法解决了轮轨滚动接触的一系列问题，诸如LI等[7-8]用显式有限元方法解决了车辆-轨道交互系统中的轮轨滚动接触问题；赵鑫团队[9-11]利用此方法对高速轮轨瞬态滚动接触行为进行了一系列研究；YANG等[12-14]通过显式有限元分析，系统地探讨了动态摩擦滚动接触建模的核心算法；西南交通大学安博洋[15-16]、刘超[17]及寇峻瑜[18]分别研究了高速车轮擦伤引起的瞬态响应、车辆曲线通过时轮轨瞬态滚动接触行为和高速车轮多边形的动态响应，以上研究均取得了令人满意的成果。上述研究在进行轮轨瞬态动力学模型计算过程中，所采用的大多为半轮对有限元模型，均没有对不同模型参数所带来的影响加以探究。显式有限元方法的计算结果与模型的网格划分、单元尺寸以及模型结构都有着密不可分的联系，因此探究不同模型参数对瞬态计算的求解影响，并引入轨面不平顺激励，明确全轮对模型的适用范围，从而为高速轮轨滚动接触问题的精细化建模提供参考。

1 三维轮轨瞬态滚动接触有限元模型

模拟我国某高速线路的车辆-轨道系统，研究不同模型参数条件下的瞬态计算模型在直线轨道上的轮轨滚动接触行为。所建立的模型将真实的车轮和钢轨几何考虑在内，车轮踏面为LMa型，轮径860 mm，钢轨廓形为CHN60，模型结构如图1所示。研究着重于高频振动，因此，模型中轮轨、轨道板均用线弹性材料模型，以便考虑车轴、车轮和轨道的弹性变形。为便于表述，建立图1所示的笛卡尔坐标系Oxyz，原点位于轮对初始位置A处轨道表面中心处，z轴和y轴分别沿纵向即滚动方向和垂向。车辆一系悬挂以上的所有部件被简化为刚体或质点MC并通过一系悬挂(KS、CS)与车轮相连。

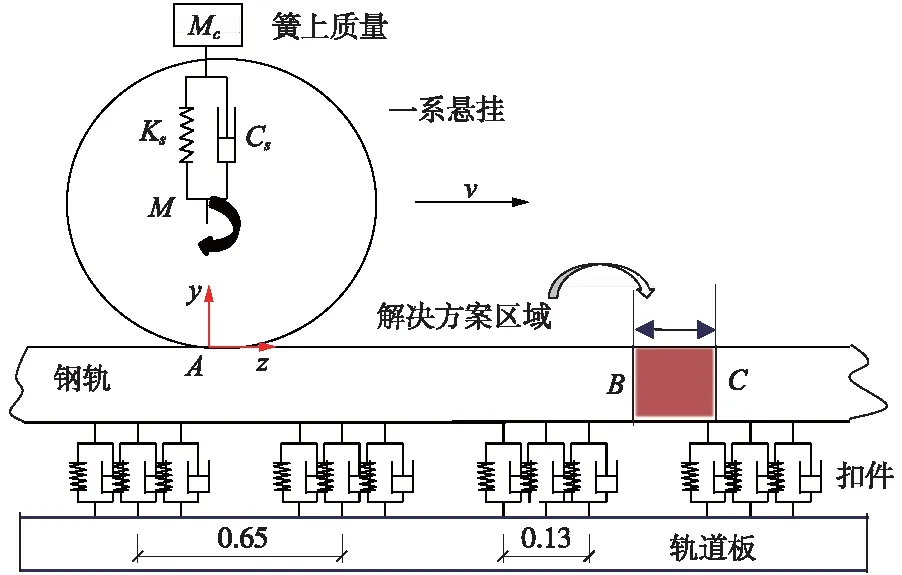
图1 模型结构示意(单位：m)

除重力荷载外，驱动扭矩是轮轨牵引摩擦接触模拟中另一个广泛使用的荷载边界条件，通常使用梁单元来获取外部施加的扭矩。如图2(a)所示，使用4个长度为L的梁单元。每个梁单元由3个节点组成：Ij(j=1，2，3，4)、J和K，其中，K节点定义方向节点。驱动节点J上施加驱动力矩M并垂直于平面S，其方向由右手定则确定，大小按照图2(b)中施加，大小随时间线性增加后保持不变。为保证结果可靠，针对轮轨系统的高速动态模拟，通常保证沙漏能量远小于系统总动能的1%，模型中沙漏系数取为0.001。具体模拟轮轨滚动接触过程时，通过在轮轴中心施加转矩M使其保持恒定的速度(“v=300 km/h”)，由图1所示的初始位置沿着钢轨向前滚动，经过动态松弛区AB后，系统基本进入稳态滚动状态，在BC段获取滚动接触解。考虑到轮轨瞬态接触是有关时间的非线性和移动载荷问题，故采用Lagrangian描述进行网格划分，其中，车轮、钢轨由8节点六面体单元离散。模型中各材料参数均参照我国某高速线路取值，见表1。

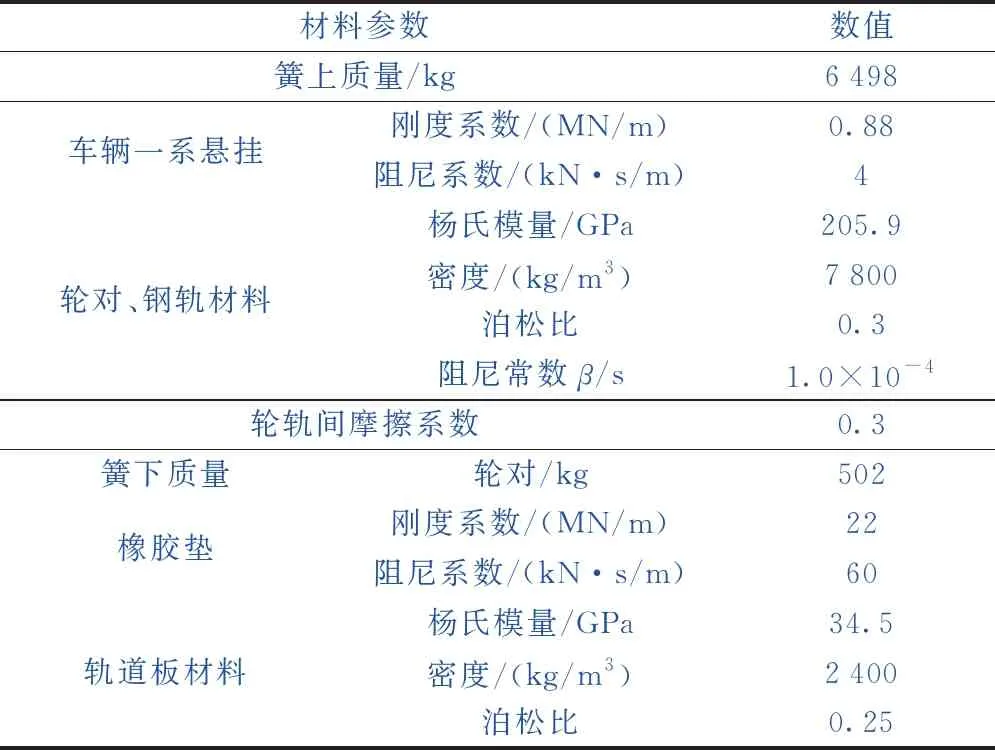
表1 有限元模型材料参数

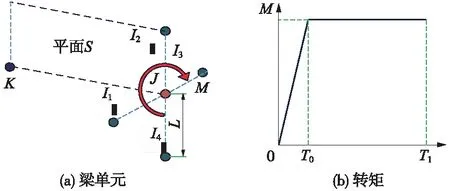
图2 施加在梁单元上的驱动力矩示意

图3为不同模型参数条件下的三维轮轨瞬态滚动接触有限元模型，分别对扣件系统、钢轨长度、轨道板及全轮对与半轮对的模型结构差异等不同参数进行可控化分析对比，从而探究不同参数条件下对模型瞬态滚动接触求解的影响。考虑到钢轨的边界条件导致数值误差，图3(a)中建立的轨道长为15.2 m，钢轨轨底坡为1∶40。图3(b)中考虑扣件系统对瞬态接触计算的影响时，建立含扣件系统钢轨长度分别为10，15.2，20，50 m的瞬态模型。此外，在考虑轨道板振动特征时，见图3(c)，其建立全扣件系统轨道长15.2 m，并在扣件下方建立轨道板材料和橡胶垫。图3(d)在图3(b)的基础上建立含扣件系统且轨道长度为15.2 m的全轮对模型，其轮对横移量为0。

图3 不同参数条件下的三维轮轨瞬态滚动接触有限元模型

2 不同参数条件下的轮轨瞬态模型求解分析

图4给出了不同参数条件下轮轨瞬态滚动接触模型以300 km/h速度稳态滚过钢轨时的轮轨垂向力随时间的变化。

由图4(a)所示，施加扣件系统的模型，车轮在进入稳态滚动区域时，其动态响应已趋于平稳，轮轨垂向力大小与轴重基本保持一致，大小为68.6 kN，总体呈现周期性波动，对比未施加扣件系统的模型求解结果可知，未添加扣件系统的模型，轮轨力虽然能够趋于稳定，但是轮轨间的激振作用明显加大，且在求解瞬态模型计算中，添加扣件系统可使滚动接触在更短时间内趋于稳定，其实质是扣件系统的阻尼起到了衰减振动的作用，提高了轮轨瞬态滚动接触的求解效率。由图4(b)中可知，钢轨长度并不能影响瞬态模型的计算结果，反而加大钢轨长度，又造成了数值计算的困难程度，因此，建议模型中钢轨长度为15 m左右为宜，即24组扣件。

图4(c)中，施加轨道板结构的模型和未施加轨道板结构的垂向力大小接近。然而存在轨道板结构的时候，其垂向力值更接近于车轮的静轮载，而且进入稳态计算时，可很好地趋于稳定状态，垂向力的浮动在5%以内。即存在轨道板结构的时候，轮轨瞬态滚动接触数值计算会更加精确，可以更好地模拟实际工况。图4(d)中展示的为半/全轮对的模型结构求解结果对比，全轮对与半轮对在瞬态滚动接触时，存在横向约束是否存在的差异，研究对比瞬态接触垂向力大小可知，右轨的轮轨接触力明显大于左轨，这是由于释放横向约束后，轮对出现一定横移量造成的偏差，全轮对模型瞬态解更加能反映出轮轨过渡时的动态响应。

图4 三维瞬态滚动接触有限元模型轮轨垂向力

3 三维轮轨瞬态滚动模型冲击分析

在高速铁路中，车轮滚动通过时所激发的频率将导致车轮及钢轨发生结构上变形，因此，在计算轮轨瞬态滚动接触之前进行模态分析是必要的。本节选取了实心轴半轮对与全轮对各自的3个典型模态分析结果，分别如图5和图6所示。

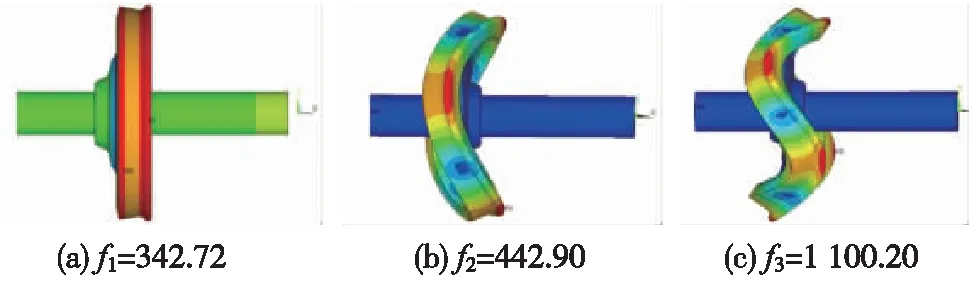
图5 施加横向约束的半轮对有限元模态分析(f为激励频率，单位:Hz)

图6 全轮对有限元模态分析(f为激励频率，单位：Hz)

钢轨轨面不平顺是激发高速铁路轮轨系统高频振动的激励源，车轮通过不平顺地段时，由于钢轨表面的不平顺，引起轮轨作用力急剧增大，使机车车辆和轨道产生剧烈振动，促使轨道和机车车辆相关部件伤损的产生和发展，从而增加维修费用[20]。基于上述模态分析的结果，对半/全轮对模型钢轨表面施加凹陷即不平顺激励，使其在轮轨瞬态滚动过程中，能够激发出对应频率下的模态变形，见式(1)

(1)

式中，f为激励频率，Hz；v为行车速度，km/h；γ为钢轨轨面不平顺长度，mm。

为方便读者理解，建立如图1模型简图中的坐标系，OZ为车轮滚动方向，钢轨表面的不平顺施加技术通过自编程序进而修改相应节点坐标值，使得钢轨缺陷的深度D在纵向和横向上分别呈余弦和抛物线分布，其对应函数[19]如下

(2)

(3)

式中，z0为钢轨纵向起始位置坐标值；x为钢轨横向坐标值；d为钢轨不平顺的最大深度，取0.1 mm；w为钢轨不平顺半宽值30 mm。

图7为轨面不平顺激励示意。

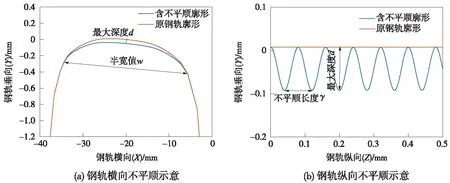
图7 短波激励示意

本节模型采用速度300 km/h，不平顺参数见表2。结合图5、图6对比分析典型半轮对与全轮对模态变形的差异，可以发现，第一组半轮对与全轮对的模态变形一样，而频率却有所差异，半轮对模态为1 100.20 Hz，全轮对模态为1 138.60 Hz；第二组半轮对与全轮对的频率在442 Hz左右，但其模态变形不一样；第三组，半轮对模态为342.72 Hz，全轮对模态为308.80 Hz，即半轮对未激发出全轮对相应频率下的模态，两者频率也不同。在实际运营中，钢轨两侧的不平顺状态几乎不一致，滚动过程中轮对两侧是相互影响的，于是为分析符合现场的全轮对两侧相互影响下与半轮对建模的瞬态求解差异，将对全轮对一侧施加轨面不平顺激励，且半轮对依照全轮对的模态频率进行施加，以此来分析对比半轮对与全轮对的瞬态求解差异。具体给出了轮轨力大小、最大接触斑等效应力的结果，如图8、图9所示。

图8 轮轨滚动接触垂向力

图9 滚动过程接触斑内最大等效应力变化趋势

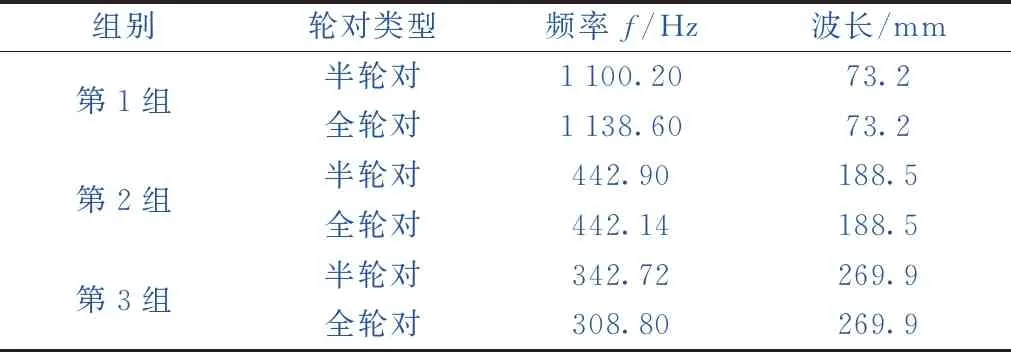
表2 不同模型的钢轨不平顺参数

图8给出了车轮以300 km/h速度滚动通过钢轨表面不平顺时的轮轨垂向力随时间的变化，从图8可以看出，半/全轮对模型在0.011 s时候，开始进入不平顺区段，此时轮轨力发生了巨大变化，呈现周期性的正弦形波动，而且峰值也是呈现出先增大后减小的趋势，相较于稳态计算过程，此时轮轨冲击作用加剧，原先维持的动态力平衡经过不平顺段已经变为更为强烈的振动响应。

通过计算可知，图8(a)中第1组工况中车轮模态变形一致，而激发的频率不一致，此时全轮对模型垂向力峰值比半轮对高出15.1%；图8(b)第2组工况两者车轮模态变形不一致，频率保持一致，全轮对左轨垂向力峰值比半轮对高出6.9%；图8(c)第3组工况半轮对模型未激发出相应的模态变形，而全轮对在此频率下进行冲击作用，此时全轮对左轨垂向力比半轮对高出5.8%左右。

上述3组工况中，全轮对模型均发生共振现象，而半轮对未激发出相应的模态，两者差异明显，可知半轮对与全轮对之间存在差异，因此在模拟轮轨冲击的工况下，需建立全轮对模型求解，以保证结果的可靠真实性。值得注意的是，在经过不平顺阶段，两种工况的垂向力峰值均呈现出先增大后减小的趋势，这是因为，此时经过了扣件系统支撑的钢轨不平顺表面，下部结构刚度增大，使得轮轨力出现了些许增加的趋势，滚过扣件系统时，此时轮轨力会逐渐减小。

图9给出了车轮滚动通过钢轨不平顺表面的轮轨接触斑内等效应力大小变化趋势，可以发现，3种工况中半轮对模型均呈现先平稳过渡然后应力增加再减小的趋势，而施加有激励一侧的全轮对轮轨间等效应力变化趋势与之接近，而未施加的则保持平稳过渡。就第1组工况而言，在半轮对车轮经过波峰时应力为628.2 MPa，全轮对车轮经过波峰时应力为717.2 MPa，两者相差14.2%，半轮对车轮经过波谷时应力为360.8 MPa，全轮对车轮经过波谷时应力为355.7 MPa，两者相差1.4%，从图9可知，轮对的冲击作用更为显著，另外两组工况与之规律保持一致。

4 结论与展望

基于三维轮轨瞬态滚动接触有限元模型，考虑不同模型参数的影响，采用ANSYS/LS-DYNA求解不同条件下车轮通过的瞬态接触解，详细对比分析了扣件系统、钢轨长度、轨道板和建模方式对轮轨瞬态接触解的影响，并结合模态分析结果，研究半轮对与全轮对的轮轨冲击效应。结论如下。

(1)扣件系统对轮轨瞬态求解的影响作用显著，添加扣件系统可使滚动接触在更短时间内趋于稳定；施加轨道板结构的模型，瞬态数值计算会更加精确，可以更好地模拟实际情况。

(2)结合模态分析结果，对半轮对与全轮对模型施加相同的钢轨顶面不平顺激励，全轮对模型均发生共振现象，而半轮对未激发出相应的模态，轮轨冲击过程中两者差异明显。因此，在模拟轮轨冲击工况下，需建立全轮对模型求解，以保证结果的可靠真实性，同时为车辆直线通过行为和模型精细化建立的有效性研究提供了必要的分析手段。

(3)轮轨冲击响应仅研究了直线段钢轨不平顺所带来的影响，未考虑到车轮磨耗对轮轨冲击所带来的不良隐患。以后的研究工作中，可进一步分析轮对单侧及双侧均存在磨耗的情况下，其瞬态轮轨动态响应和轮对间的激励和传递效果。另外，对于车轮次表层裂纹可以同时展开研究，对于实际运营车辆中的车轮璇修问题提供理论支持。