盾构下穿既有隧道位移控制施工参数多目标优化

曾铁梅,王金峰,吴贤国,田金科,陶文涛,杨 赛,陈 彬

(1.武汉地铁集团有限公司,武汉 430070； 2.华中科技大学土木工程与力学学院,武汉 430074)

引言

随着我国地下轨道交通系统的广泛兴起，盾构隧道近接施工工程越来越多，而隧道在盾构施工过程中可能出现的最大风险就是过度的地面水平位移和沉降位移。因此，为保证地铁隧道施工和运营安全，采取可靠措施将位移控制在安全合理的范围中具有重要意义。

目前，国内外大量文献从对既有构筑物沉降变形影响角度研究隧道近接施工的规律，主要有3种研究方法：理论公式[1]、数值模拟[2-4]、模型试验[5]。理论公式法研究如WANG Y等[6]基于Winkler地基模型推导了隧道开挖引起的邻近管线变形微分方程，以分析隆起或沉降变形情况；周泽林等[7]基于镜像汇源法和盾构隧道土体非等向收缩模式，建立盾构隧道引起的已建隧道变形控制方程。数值模拟研究如LI M等[8]采用FLAC3D建立三维数值模拟模型，分析了基坑分阶段施工对车站及既有地铁隧道的影响；杨成永等[9]通过数值模拟研究双线盾构近距下穿既有隧道的施工沉降规律及控制；马文辉等[10]对隧道沉降进行数值模拟并分析监测数据，对盾构下穿施工参数进行控制。模型试验法研究如李鹏等[11]利用离心模型试验模拟了新建隧道上穿越江隧道的施工过程，研究新建隧道隆起的规律；MA S等[12]进行了一系列三维离心机模型试验，研究不同深度的并列双隧道对干砂中既有埋藏管道的影响。以上方法均对盾构近接施工的沉降研究有一定价值，但理论公式法往往只适用于特定情况且精度较差，数值模拟精度一般但耗时耗力，模型试验精度较高但仪器昂贵且耗费时间。

为控制盾构施工下穿既有隧道的影响，需研究盾构施工参数优化对既有隧道变形进行控制。为此，提出一种基于GA-LSSVM与NSGA-Ⅱ算法相结合的完整智能算法框架，利用GA-LSSVM对既有隧道底部水平位移和沉降位移进行高精度非线性预测，再以GA-LSSVM得到的非线性预测关系作为适应度函数，研发NSGA-Ⅱ调用非线性预测关系适应度函数算法，从而对盾构施工参数进行智能多目标优化，获得合理可靠的参数取值。

1 理论基础

1.1 GA-LSSVM基本原理

1.1.1 最小二乘支持向量机

最小二乘支持向量机(LSSVM)对传统的SVM进行了改进，采用最小二乘线性系统作为损失函数，将SVM中优化问题的不等式约束转化等式约束[13]。设训练的样本集(xi，yi)，xi∈Rn，yi∈{-1，+1}，i=1，2，…，N。其中，N为训练样本总数；n为样本空间维数；y为样本类别标签。根据结构风险最小化原则，LSSVM分类问题的最优分类面由以下优化问题得到

(1)

式中，φ(·)为非线性映射；ω为权重；ξi为误差变量；c>0为惩罚系数。于是，LSSVM的优化问题所对应的Lagrange函数为

(2)

式中，Lagrange乘子ai>0(i=1，2，…，N)。对式(1)进行优化，使ω，b，ai，ξi的偏导数为0，再利用Mercer条件可得，φ(xj)=yiyjK(xi，xj)，其中，K(xi，xj)为核函数。用最小二乘法得到最优回归函数为

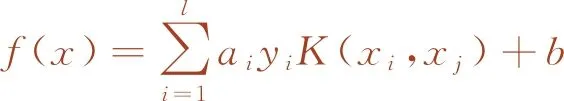
(3)

1.1.2 GA-LSSVM模型

LSSVM参数选择对模型预测精度至关重要，主要是惩罚参数c和核参数(如径向基函数中的σ2)的选取。目前，对于参数的优化方法主要包括：基于网格搜索的交叉验证、智能优化算法。用网格划分来寻找最佳的参数c和g，可以全局最优解但在更大范围内寻优很费时，而采用智能优化算法可以解决这个问题，故采用遗传算法对LSSVM的参数进行优化核改进，寻找最优的LSSVM回归模型参数。

利用GA算法对LSSVM的参数进行优化大致步骤如下。

(1)种群初始化：根据问题特性设计合适的初始化操作，即对种群中的N个个体进行初始化操作。

(2)个体评价：根据优化的目标函数计算种群中所有个体的适应值(fitness value)。

(3)遗传算法操作：在适应度的基础上，设置种群最大迭代次数为200次，通过个体选择后，以0.9的交叉概率和0.1的变异概率进行交叉变异操作，生成新一代染色体。

(4)循环(3)的流程直至达到最大迭代次数。

1.2 NSGA-II算法基本原理

遗传算法是一种基于达尔文进化理论的最优规划算法[14]，2002年DEB、AGRAWA等人在传统遗传算法的基础上提出带精英策略的非支配排序遗传算法(NSGA-Ⅱ)。NSGA-Ⅱ的核心特点是快速非支配排序和拥挤度[15]，具体原理如下。

快速非支配排序：传统遗传算法的非支配排序是O(MN3)(M为目标数，N为种群大小)，经过改进后，NSGA-Ⅱ算法的非支配排序是O(MN2)，提升了种群的排列速度，故称为快速非支配排序。

拥挤度：在计算拥挤距离时，首先对种群进行升序排序，同时设置第一个、最后一个拥挤距离为无穷大，其中，第i个解的拥挤距离计算如式(4)。

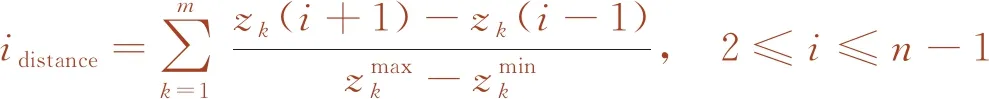
(4)

式中，zk(i)为第i个解的第k个目标函数值；m为目标函数的个数；zkmax和zkmin分别为第k个目标函数的最大值和最小值；n为指定前沿解的个数。

1.3 基于GA-LSSVM与NSGA-Ⅱ算法的多目标优化模型构建

工程中很多输入变量和输出结果之间是高度非线性的关系，为获取两者之间具体函数形式，可利用GA-LSSVM模型替代传统的数学函数。并用GA-LSSVM模型作为遗传算法适应度函数，实现更精确的优化。GA-LSSVM与NSGAII算法的具体流程如图1所示。

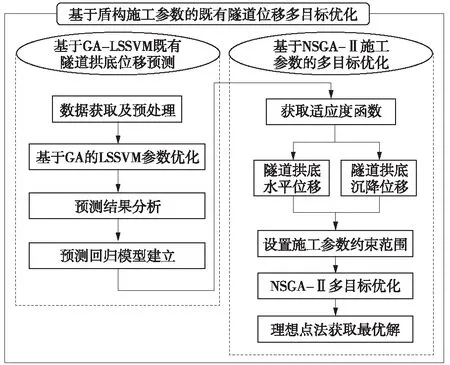
图1 基于GA-LSSVM与NSGA-Ⅱ算法的多目标优化模型流程

1.3.1 基于GA-LSSVM既有隧道底部位移预测

(1)数据获取及预处理

通过查阅大量相关文献并根据实际工程情况，选取对既有隧道变形较为敏感的因素作为隧道底部位移预测输入参数，并将隧道底部水平位移和沉降位移作为预测输出参数。

为防止样本出现数据过大或过小而导致数据被淹没或不收敛的情况，需对样本数据进行预处理[16]。将输入变量和输出归一化到[-1，1]区间，可使每个参数在预测过程中起到效果。

(2)核函数参数优化

核函数对GA-LSSVM预测精度有很大影响，研究应根据实验对象特点来选择合适的核函数[17]。由于高斯核函数在有径向基核函数优势的同时还保持良好的抗干扰能力，故将采用高斯核函数作为预测模型的核函数进行研究，如式(5)。

(5)

式中，xi为输入变量；x为输出变量。

在确定核函数后，为确保GA-LSSVM的泛化水平，将采用K折交叉验证，利用遗传算法进行核函数宽度参数g和惩罚系数c优化，K折交叉验证常用于GA-LSSVM模型性能的验证，可以避免GA-LSSVM模型欠学习或过学习状态。

(3)预测结果分析

为验证GA-LSSVM模型的预测精度，引入拟合优度R2来检验。拟合优度R2表示预测值与真实值之间的拟合效果，拟合优度越接近1，说明预测效果越高，如式(6)。

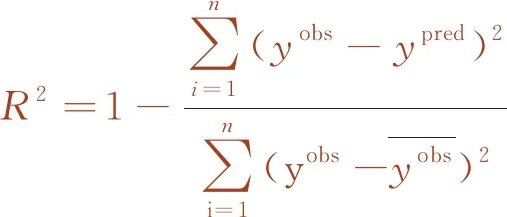
(6)

1.3.2 NSGA-Ⅱ多目标优化

(1)建立目标函数

基于GA-LSSVM的隧道底部水平位移和沉降位移目标函数，引入GA-LSSVM隧道底部位移回归预测算法替代传统数学函数作为多目标遗传算法中的适应度函数，从而表示输入变量与输出目标之间存在复杂非线性关系。

由公式(3)可知，隧道底部水平位移回归函数ming1和沉降位移回归函数ming2分别表示为

ming1(ga-lssvm(x1，x2，…，xn))

(7)

ming2(ga-lssvm(x1，x2，…，xn))

(8)

(2)建立决策变量约束条件

为使得生成的方案更加合理可行，需对方案生成时的各个因素设定限制范围，形成变量的约束条件，约束条件的一般形式如下

bil≤xi≤biu

(9)

式中，xi为第i个设计参数，bil和biu分别为第i个设计参数值的下限和上限。

(3)NSGA-Ⅱ多目标优化

当隧道底部位移目标函数及范围确定后，利用NSGA-Ⅱ算法进行多目标优化，可以找到隧道底部位移的Pareto最优解集。与传统GA相比，NSGA-Ⅱ算法有两个不同关键步骤。

①在设置初始种群后，NSGA-Ⅱ算法将通过快速非支配排序后，利用遗传机制：选择、交叉、变异后获得第一批子代种群。

②在第二代种群进化后进行父、子代合并，通过快速非支配排序之后计算个体之间拥挤度，根据非支配关系和个体间拥挤距离确定新种群，通过3个遗传机制产生新的子代种群。

(4)基于理想点法获取最优解

利用NSGA-Ⅱ算法获取的Pareto最优解集并不是唯一的解，为获取获得唯一最优解，可采用理想点法[18]。理想点是指利用各个目标对用最优值所对应的最优值组成的点E(ηEpoint，ZEpoint)。

找出对应的理想点后，计算Pareto最优解图中各个最优解到理想点之间的距离，计算公式如下

(10)

式中，(ηpareto，Zpareto)为最优Pareto前沿点对应的坐标；(ηEpoint，ZEpoint)为理想点对应的坐标。通过计算距离函数，最优点是距理想点最小距离的点

Uopt=min(Un)

(11)

因此，利用理想点法可从Pareto前沿解集中确定，使得多目标函数达到最优的一组最优解。

2 基于GA-LSSVM与NSGA-II算法的盾构施工参数多目标优化

以轨道交通某地铁4号线盾构隧道下穿地铁2号线工程为依托，2号线与4号线为上下交叉隧道，平面投影的夹角近似90°，盾构机直径6.2 m，长度7.5 m，既有隧道管片外径为6.2 m。既有隧道所处土层为软黏土，泊松比0.28，土体弹性模量24.5 MPa，土体重度γ=20 kN/m3，衬砌结构厚0.3 m，内摩擦角φ=30.5°，黏聚力c=25.2 kPa，隧道埋深18 m，衬砌结构混凝土强度等级C50，弹性模量Ec=34.5 GPa。

盾构隧道与既有隧道两者的空间位置关系为：上部隧道拱顶埋深8.2 m，下部隧道拱顶埋深14.4 m，上下隧道净距3.1 m，两隧道垂直交叉范围长6.2 m。需解决的问题是针对近距离下穿盾构施工，研究盾构施工参数优化对近接既有隧道变形控制的影响。

2.1 基于GA-LSSVM既有隧道底部位移预测2.1.1 数据获取与预处理

文献[19-21]研究表明，既有隧道变形较为敏感的因素有：刀盘扭矩、顶推力、泡沫量、注浆量、出土量及穿越地层的实际土压力。因此，将以上述6个参数作为输入参数，并将既有隧道底部水平位移和底部沉降位移作为预测输出参数，选取的GA-LSSVM训练样本数据及其中每个输入参数的取值范围见表1。

表1 训练样本

2.1.2 核函数参数优化

根据1.3.1节的分析，采用Standard Scale将训练样本进行标准化，采用GA算法优化LSSVM的模型参数c、g和p，将LSSVM模型参数中的惩罚系数c的搜索范围设置为[0，100]，核函数宽度参数g的搜索范围为[0，1 000]，p的搜索范围为[0.01，1]。选择5折交叉验证法对GA寻优得到的核函数宽度参数g和惩罚系数c进行建模验证选优，分别得到隧道底部水平位移和沉降位移LSSVM预测模型的最优参数，水平位移、沉降位移预测参数优化结果如图2所示。

图2 GA优化LSSVM模型参数

从图2(a)中可知，惩罚系数bestc=17.494 9，核函数参数bestg=915.08，p=0.434 52，此时均方根误差最小为mse=0.083 303。

同样，从图2(b)可知，惩罚系数bestc=31.106 5，核函数参数bestg=0.135 42，p=0.443 8，此时均方误差值最小为mse=0.077 07。

2.1.3 预测结果分析

基于GA-LSSVM核函数参数优化的结果，利用训练集进行学习模拟，分别建立GA-LSSVM隧道底部水平位移、沉降位移预测模型，根据上述步骤，隧道底部位移预测结果如图3所示。

图3 GA-LSSVM位移预测

从图3(a)可以发现，GA-LSSVM模型能够准确预测隧道底部水平位移变化。基于GA-LSSVM模型对水平位移的预测拟合优度为0.998 7，该模型拟合结果很好，其预测值与实际值之间误差非常小。

从图3(b)可以发现，GA-LSSVM模型也能够准确预测隧道底部沉降位移变化。基于GA-LSSVM模型对沉降位移的预测拟合优度为0.996 4，模型拟合结果同样很好，样本的预测值与试验值十分接近。

2.2 基于NSGA-Ⅱ的既有隧道底部位移多目标优化

2.2.1 建立目标函数

在GA-LSSVM预测模型的基础上，应用带精英策略的非支配排序的遗传算法(NSGA-Ⅱ)对既有隧道底部位移进行多目标优化。优化目标为同时实现水平及沉降位移最小化，对应的优化模型目标函数由式(7)、式(8)得到。

(1)隧道底部水平位移目标函数

ming1(ga-lssvm(x1，x2，…，x6))

(2)隧道底部沉降位移目标函数

ming2(ga-lssvm(x1，x2，…，x6))

式中，x1、x2、x3、x4、x5、x6分别为土舱压力、泡沫量、同步注浆量、掘进速度、刀盘扭矩及顶推力。

2.2.2 建立变量约束范围

由于隧道条件的复杂性及不同隧道项目的独特性，项目各个影响参数的范围无法由工程相关规范所确定，因此，将对所采集的数据进行排列，且以各个参数的最大值和最小值为影响参数的上下限，如式(12)所示

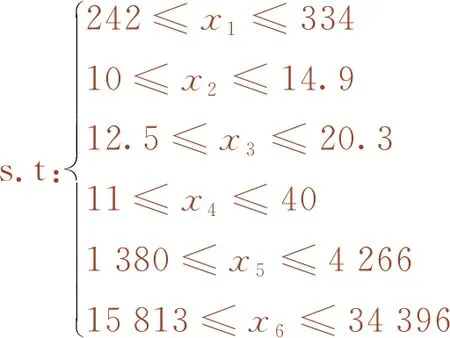
(12)

式中，x1、x2、x3、x4、x5与x6分别为土舱压力、泡沫量、同步注浆量、掘进速度、刀盘扭矩及顶推力。

2.2.3 基于NSGA-Ⅱ的多目标优化

当隧道底部位移目标函数及范围确定后，利用NSGA-Ⅱ算法对盾构施工参数进行多目标优化，交叉概率取0.9，初始种群大小取40，经过200次迭代寻优后，NSGA-Ⅱ算法得到相应的非支配Pareto前沿解集，见图4。

图4 Pareto前沿解集

由图4可以看出，随着隧道底部水平位移的减小，沉降位移在逐渐增大，根据NSGA-II算法获得的非支配最优解并不是唯一的，要使两个优化目标同时达到较优的状态还需进一步决策。

一般常采用理想点法从Pareto前沿中获得最优解，根据图5的结果找到两个目标均为最小值时所构成的理想点E(1.02，5.75)，通过计算最优Pareto前沿图中的40个最优解到理想点的距离，即理想点公式，选取距离理想点最近点的坐标作为两个目标的最优值。

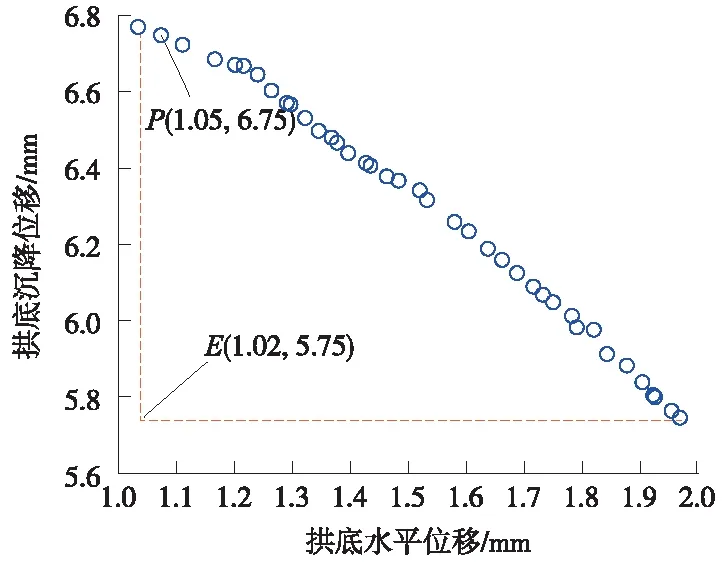
图5 理想点及最优解结果

通过计算，由图5可知，基于理想点法得到距离理想点E最小的P点坐标为(1.05，6.75)，表示此时隧道底部水平位移为1.05 m m，沉降位移为6.75 mm，相较于原始数据样本中水平位移和沉降位移的平均值1.59 mm和7.46 mm都有了明显的改善，分别减少了33.96%和9.52%。在该条件下盾构施工参数组合分别为土舱压力242 kPa，泡沫量14.74 m3，同步注浆量19.44 m3，掘进速度11 mm/min，刀盘扭矩1 380 kN·m，顶推力3 396 kN。

针对盾构下穿既有隧道施工实际情况，结合施工监测信息的反馈，综合考虑技术和可操作性等，以Pareto前沿优化所得参数范围作为参考，提出盾构施工参数设定范围控制建议值，如表2所示。

表2 盾构施工参数设置范围建议值

3 结论

提出一种GA-LSSVM结合NSGA-Ⅱ的智能算法及模型，不仅实现了盾构隧道下穿既有隧道底部水平位移和沉降位移的高精度预测，而且通过引入多个非线性预测回归函数作为优化目标，结合数据范围可反向得到优化的盾构施工参数组合，具有重要的工程价值。

(1)建立了一种基于GA-LSSVM与NSGA-Ⅱ相结合的多目标优化模型，首先对隧道底部水平位移和沉降位移采用GA-LSSVM模型进行高精度预测，并以隧道底部水平位移和沉降位移的预测回归函数分别作为适应度函数，结合工程项目实际情况建立盾构施工参数约束条件，利用NSGA-Ⅱ算法进行多目标优化，得到盾构施工参数最优值。

(2)针对传统网格搜索法参数寻优的缺点，选取土舱压力、泡沫量、同步注浆量、掘进速度、刀盘扭矩及顶推力为输入参数，提出基于GA-LSSVM既有隧道底部位移回归预测模型。其中，对隧道底部水平位移预测的拟合优度为0.998 7；对隧道底部水平位移预测的拟合优度为0.996 4，模型精度较高、预测效果良好，体现了该方法的可行性及GA算法改进的有效性。

(3)利用NSGA-Ⅱ算法基于盾构施工参数进行多目标优化后，可实现隧道底部水平位移与沉降位移的同时最小化，即取值分别为1.05，6.75 mm，与原始数据的平均值相比分别减小了34%和10%左右。此时，对应土舱压力242 kPa，泡沫量14.74 m3，同步注浆量19.44 m3，掘进速度11 mm/min，刀盘扭矩1 380 kN·m，顶推力3 396 kN。据此确定盾构施工参数合理控制范围，以便对盾构施工前的参数组合进行调整，控制既有隧道底部沉降和水平位移，证明了该模型在盾构施工参数优化过程的实用性及可靠性。