复合式路面疲劳裂纹扩展寿命模型及子程序开发应用

孔令云, 阮庆松

(重庆交通大学 土木工程学院,重庆 400074)

0 引 言

目前,复合式路面在我国已得到广泛应用,但随着使用年限增加,局部路段逐渐产生各种病害,其主要类型为裂缝,使路面变得松散,需要对路面进行修补[1]。而疲劳开裂是复合式路面的主要破坏形式之一,它主要分为2个阶段,第1阶段为疲劳裂纹形成阶段,第2阶段为疲劳裂纹扩展阶段[2]。在第1阶段,材料的微观缺陷发展成为宏观的裂纹,在第2阶段,宏观裂纹扩展直至材料断裂失效。本文研究第2阶段的疲劳寿命计算问题。

疲劳寿命的计算以断裂力学理论为基础,目前主要采用Paris公式进行计算。由于2种结构层材料性能差异较大,在水泥混凝土层容易产生裂缝,而在沥青层容易产生反射裂缝[3]。对于路面裂缝扩展行为,相关研究大多通过对沥青小梁进行三点或四点弯曲疲劳试验或数值模拟来获取[4]。文献[5]采用数值方法研究了多层沥青路面自上而下和自下而上裂缝的疲劳寿命、裂缝扩展轨迹和应力强度因子;文献[6]建立2个三维有限元模型,分析路面结构的力学响应,解决了加铺层实际疲劳寿命明显低于设计值的问题。在计算水平应变时,大多数沥青路面的力学设计方法都认为路面层是完全黏结的,自下而上的裂缝是疲劳破坏的关键类型;路面层间黏结状况是影响路面使用性能的重要因素之一。文献[7]以表面水平拉伸应变为基础,研究了界面结合条件对自上而下疲劳裂纹的影响。

近年来,运用ABAQUS软件自带的扩展有限元方法,对混凝土、沥青混合料等裂缝扩展行为进行数值模拟的研究成果较丰富[8-10]。文献[11]对含预设裂缝沥青复合小梁进行疲劳试验,探讨梁底部的支撑方式和预设裂缝位置对于复合小梁裂缝扩展行为和疲劳寿命的影响,借助ABAQUS平台的扩展有限元方法模拟了复合梁的裂缝扩展路径,并将模拟结果与试验结果进行对比;文献[12]采用室内MTS疲劳加载试验和滚动荷载疲劳试验研究防治反射裂缝的措施,但其施工工艺复杂。

通过有限元软件能够模拟裂缝的产生[13],但直接采用原有限元软件计算,需要建立不同裂纹长度所对应的模型,这将增加建模的工作量和计算代价。

在数值解法中,虚拟裂纹闭合法(virtual crack closure technique,VCCT)计算简便,且易于编程,可以通过现有有限元软件的子程序计算裂纹未扩展时某一点能量释放率。VCCT虽然在路面结构计算中运用较少,但它是一种计算代价较小、计算精度较高的数值方法。因此,本文以某试验路段的路面结构为例,采用该方法计算复合式路面结构的应力强度因子及疲劳裂纹扩展寿命。

本文基于足尺试验的隧道路面结构优化项目,依托工程为建德—金华(建金)高速,在清水塘隧道右洞铺设试验路段进行现场加速加载试验,采用现场试验路段的路面结构进行模拟计算。

1 疲劳裂纹扩展寿命理论模型

1.1 模型理论基础

1.1.1 断裂力学与疲劳裂纹扩展理论相关知识

断裂力学是一门研究带裂纹物体在外界作用下力学响应的学科,它是研究疲劳现象的理论基础,以能量释放率和应力强度因子为主要参数。Griffith采用能量平衡的观点建立了裂纹扩展准则[14-15],该准则被称为G准则,物理参量G称为能量释放率。应力强度因子的概念由Irwin首次提出,结构开裂的临界条件是裂纹尖端的应力强度因子达到材料的断裂韧性,此即应力强度因子断裂准则或者K准则[16]。

结构在外界周期性交变荷载作用下,如果达到了临界条件,其内部裂纹会发生扩展。裂纹扩展的快慢程度以裂纹扩展速率表示,记为da/dN,它表示外界荷载每作用1个周期所引起的裂纹扩展量[17],a为半裂纹长度,N为荷载作用循环次数。关于疲劳裂纹扩展速率da/dN与其他参量之间的关系,常用的公式有Paris公式、Walker公式、Forman公式等[18]。依据Paris公式,da/dN是应力强度因子的函数,因此,在进行疲劳寿命计算前,必须求得结构中的应力强度因子。理论上,只有几何形状规则且受力简单的结构才有应力强度因子的解析解,大部分工程实例为相对复杂的结构,而Paris公式只适用于纯张开型裂纹的扩展,因此,需采用修正后的Paris公式,即广义Paris公式[2]。

1.1.2 VCCT

VCCT由Rybicki和 Kanninen 首先提出[19],这种方法起初是用于解决二维裂纹中的能量释放率问题,文献[20]将其推广至三维情况。VCCT的优势在于,在使用有限元模拟裂纹扩展时不需要重新划分网格,大大降低了计算难度,且精度较高。利用该方法容易求得能量释放率等参数。文献[18]采用大型通用有限元软件结合用户自定义单元(user-defined elements,UEL)子程序开发了模拟三维裂纹扩展的单元,本文在此基础上编写适用于路面结构开裂的子程序,通过有限元软件主程序调用,以计算路面结构在裂纹扩展中的能量释放率。

VCCT的核心思想是裂纹扩展时释放的能量等于将裂纹闭合1个扩展增量所需的功,同时该方法假设虚拟裂纹尖端后面的张开位移和实际裂纹尖端后面的张开位移近似相等[20]。因此,如果能求得裂纹体的能量释放率,那么可以利用应力强度因子计算公式求出应力强度因子,再利用Paris公式求出疲劳裂纹扩展寿命。

1.2 疲劳裂纹扩展寿命理论模型建立思路

为计算复合路面疲劳裂纹扩展寿命,本文基于VCCT,建立了理论模型,其基本流程如下:首先,通过有限元软件结合子程序UEL计算能量释放率(G),然后通过应力强度因子计算公式得到有效应力强度因子Keff,最后通过相关公式计算得到裂缝扩展寿命NP。

(1) 能量释放率(G)的计算。基于VCCT理论,借助ABAQUS有限元分析软件,将裂纹面均划分为同等大小的网格,以便计算裂纹扩展面积。通过编写子程序UEL获取裂纹尖端节点的节点力和裂纹尖端后面节点的张开位移,利用相关公式计算得到能量释放率GⅠ、GⅡ。

(2) 应力强度因子(Keff)的计算。断裂力学的早期发展是建立在线弹性理论基础上的,在一定条件下可以看作是理想的线弹性材料,文献[21-23]引入塑性功,在设想裂纹尖端塑性区尺寸远远小于裂纹尺寸和其他特征尺寸的前提下,将线弹性断裂理论成功应用到常用的工程材料中。假设裂纹沿预设裂纹面拓展,在平面应力状态下,根据上述能量释放率(G)的计算结果,计算裂缝尖端应力强度因子KⅠ、KⅡ[17],再计算有效应力强度因子Keff[2]。

KⅠ、KⅡ、Keff计算公式为:

(1)

(2)

其中,E为弹性模量。

(3) 裂缝疲劳扩展寿命计算。根据上述应力强度因子计算结果,利用广义Paris公式计算裂缝每扩展a的寿命,其表达式[2]为:

(3)

(4)

(5)

根据计算得到的da/dN瞬时值,利用积分计算裂纹从a0扩展至an的疲劳裂纹扩展寿命NP,即

(6)

2 模型前处理

2.1 几何模型与材料参数

依托工程现场加速加载试验,参照试验路段的路面结构,取路面的计算模型为6.00 m×3.00 m×3.75 m,行车方向沿z轴负方向,预设裂纹面剖面图如图1所示(单位为m)。

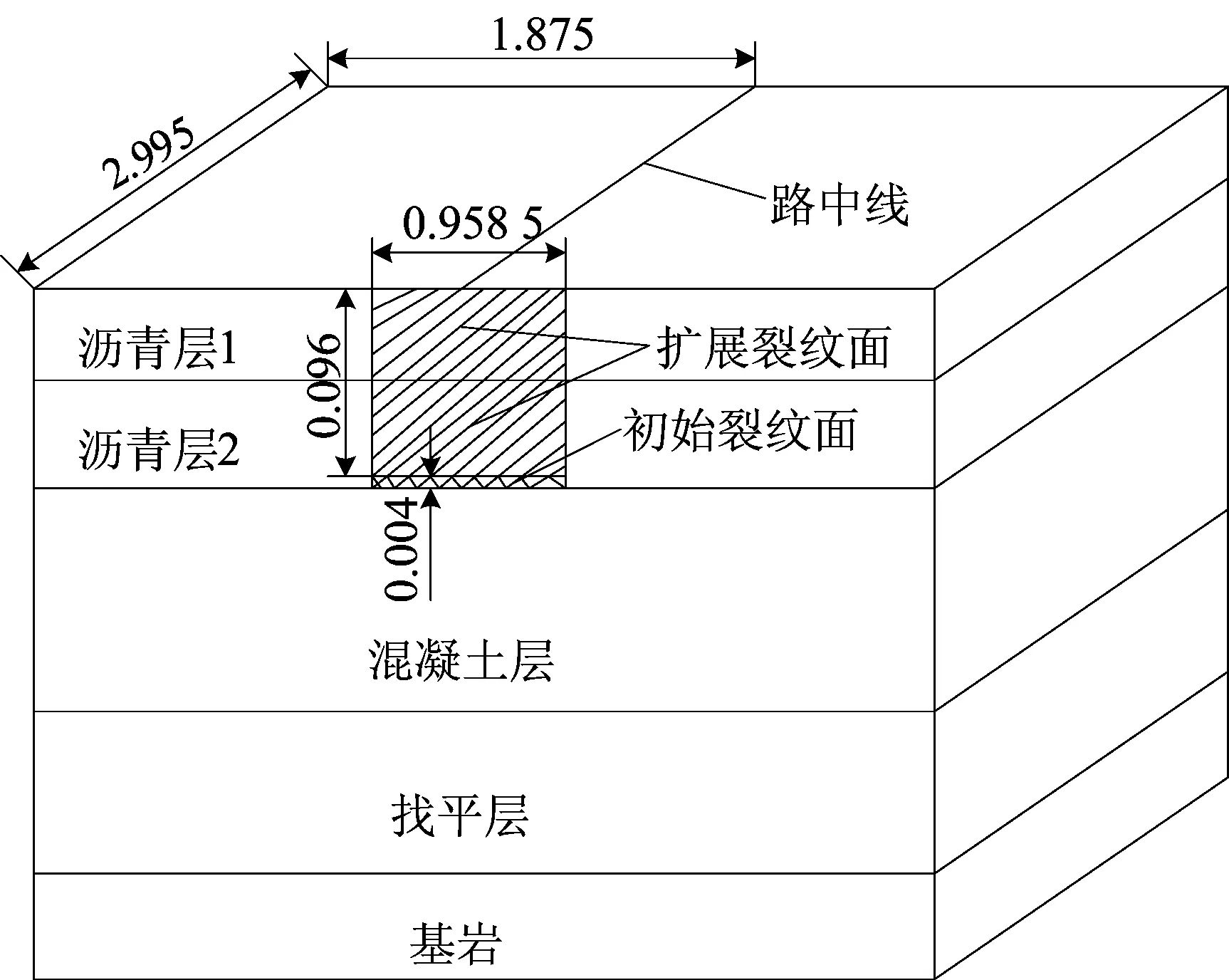
图1 预设裂纹面剖面图

路面结构各层厚度与材料属性见表1所列。混凝土层采用切缝形式,切缝深度为54 mm,切缝宽度为10 mm,如图2所示(单位为mm)。

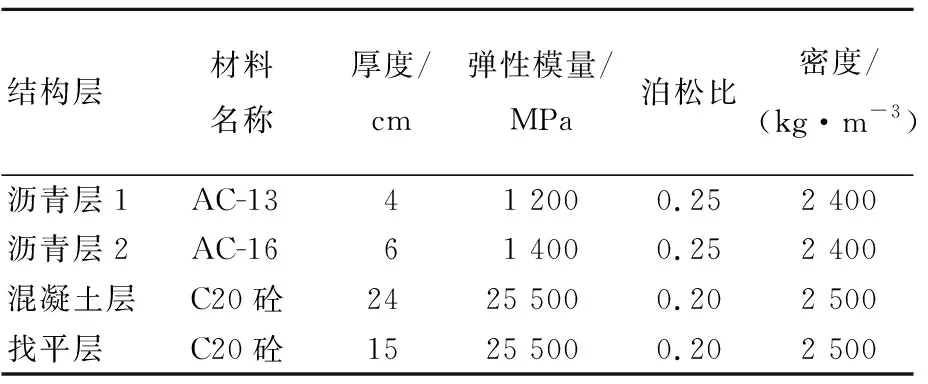
表1 路面结构层厚度与材料属性

图2 预设裂纹面侧视图

VCCT要求预设裂纹面。预设裂纹面包括初始裂纹面、扩展裂纹面2个部分,两者均为矩形。由计算结果知,裂纹出现初期每拓展0.004 m时的能量释放率相比于末期可忽略不计,对最终疲劳寿命计算影响不大,故取1个网格宽度为初始裂纹面深度,即初始裂纹面宽0.958 5 m,深0.004 m。扩展裂纹面宽0.958 5 m,深0.096 m,如图1、图2所示。

2.2 荷载

荷载采用均布荷载,其作用位置如图3所示(单位为m),即图3中阴影部分。荷载垂直于路面,其方向竖直向下。荷载位置位于预设裂纹面一侧,且关于路中线对称。

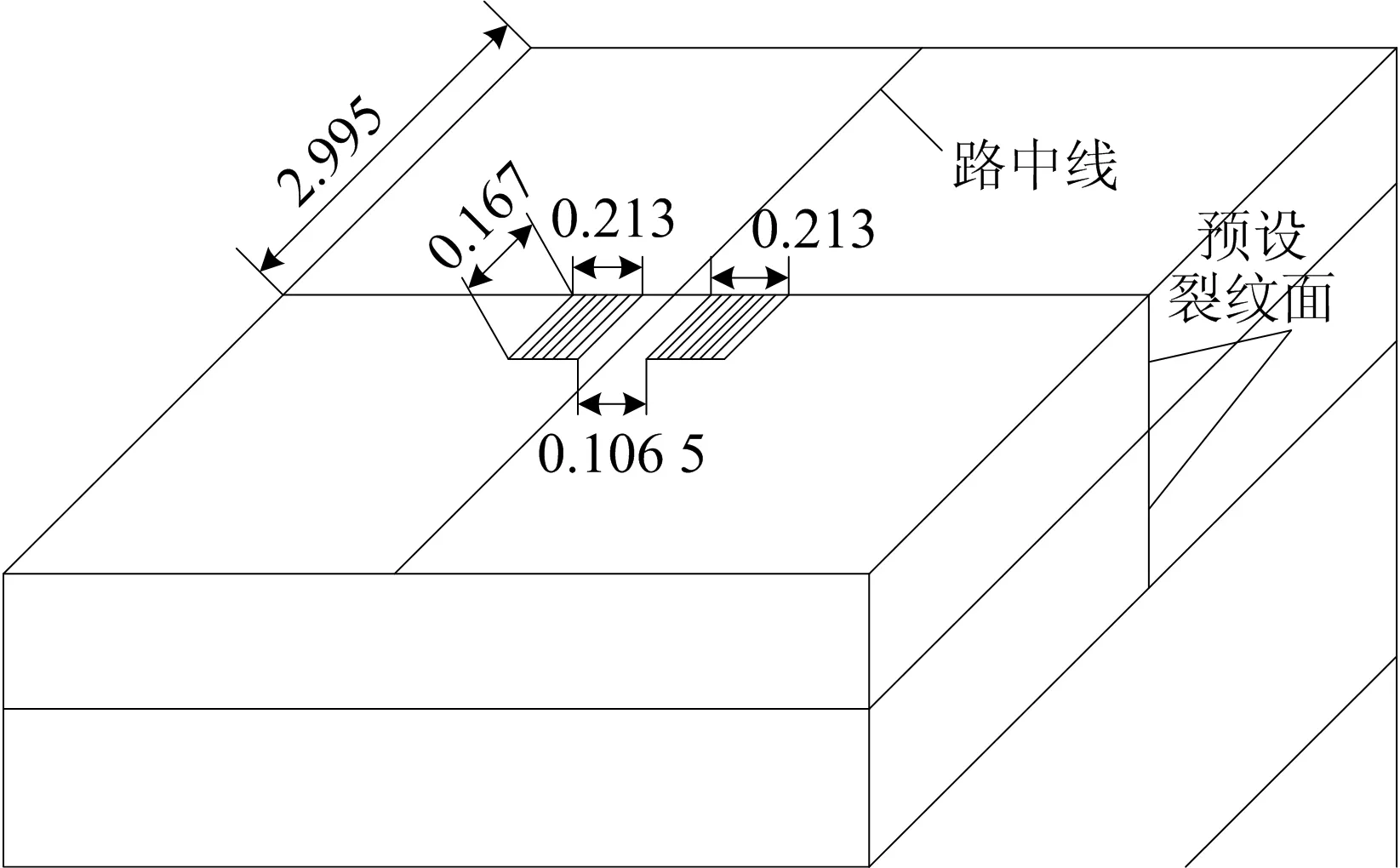
图3 荷载作用位置

因为VCCT只能采用有限元软件的Standard求解器,只能采用静态荷载,所以需要将标准荷载放大以模拟动态荷载效应。文献[24]经有限元分析得出,动态荷载作用下沿行车方向水平正应力是静态荷载的1.454倍,为保证计算的疲劳寿命偏安全,取荷载放大系数为1.5。标准荷载p0=0.7 MPa,施加的荷载大小为p=1.5p0= 1.05 MPa。

2.3 裂纹面的网格划分

裂纹面上的网格均划分为同一大小的矩形,其长0.053 25 m,宽0.004 m,由此求得裂纹扩展面积为:

ΔA=2×0.053 25 m×0.004 m=0.004 26 m2。

预设裂纹面上网格划分如图4所示。

图4 裂纹面网格划分

3 有限元模拟计算及结果分析

3.1 裂纹扩展能量释放率计算

VCCT计算简便,且易于编程。通过现有有限元软件的子程序可以计算裂纹未扩展时某一点能量释放率。若直接采用原有限元软件计算,则需要建立不同裂纹长度所对应的模型,即如果要计算n种裂纹长度对应的能量释放率,就需要建立n个模型,这必将增加建模的工作量和计算代价。本文在此基础上进行改进,编写适用于路面结构开裂的子程序使得裂纹能够扩展,并计算不同裂纹长度所对应的能量释放率。这种改进在计算n种裂纹长度对应的能量释放率时只需1个模型,因此能大大减小建模工作量和计算代价。

在有限元软件中建立几何模型并计算,结合子程序得出疲劳裂纹扩展中的能量释放率GⅠ、GⅡ,结果见表2所列。

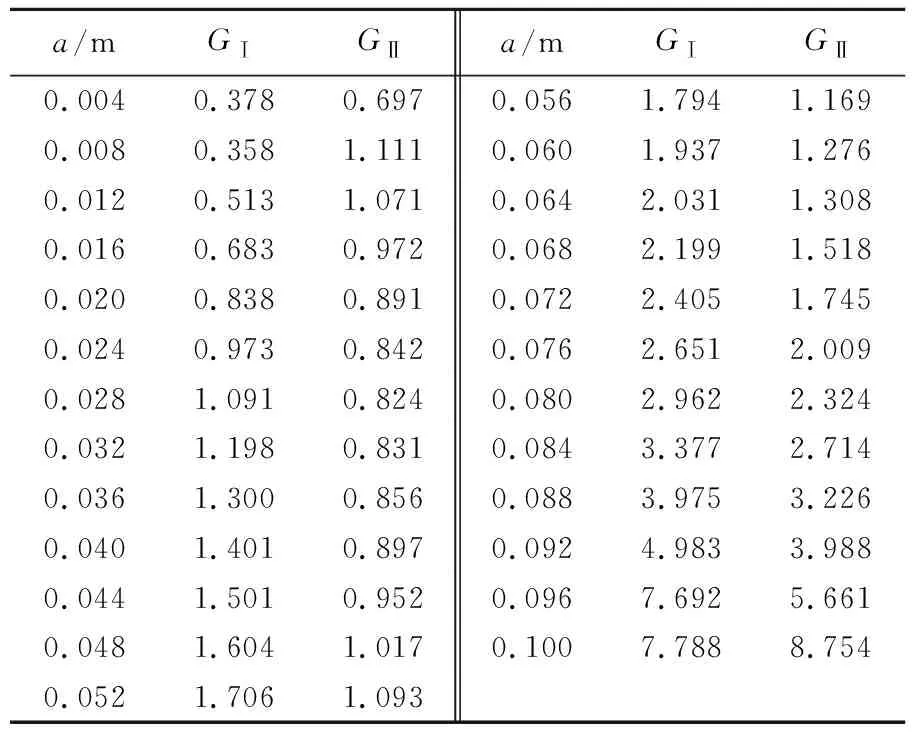
表2 能量释放率计算结果

能量释放率G的数值在输出的.dat文件中查看。用于计算G的程序操作步骤如下:

(1) 生成.inp文件。在ABAQUS软件中建立道路层状体系模型,在疲劳开裂的位置预设裂纹。对模型进行网格划分后,将裂纹两侧的节点设置在2个不同的set集合,以提取裂纹上的节点编号与节点坐标。设置荷载和边界条件,输出.inp文件,即ABAQUS模型输出文件。

(2) .inp文件修改。将生成的.inp文件中提取出的裂纹两侧节点编号和节点坐标分别转换成矩阵形式,称为节点信息矩阵。该矩阵共3列,其中前2列存储节点的x、y坐标值,第3列为节点编号。将两侧的节点信息矩阵同时导入自编程的Matlab程序中,生成自定义单元,并写入.inp文件。

生成自定义单元流程如图5所示。

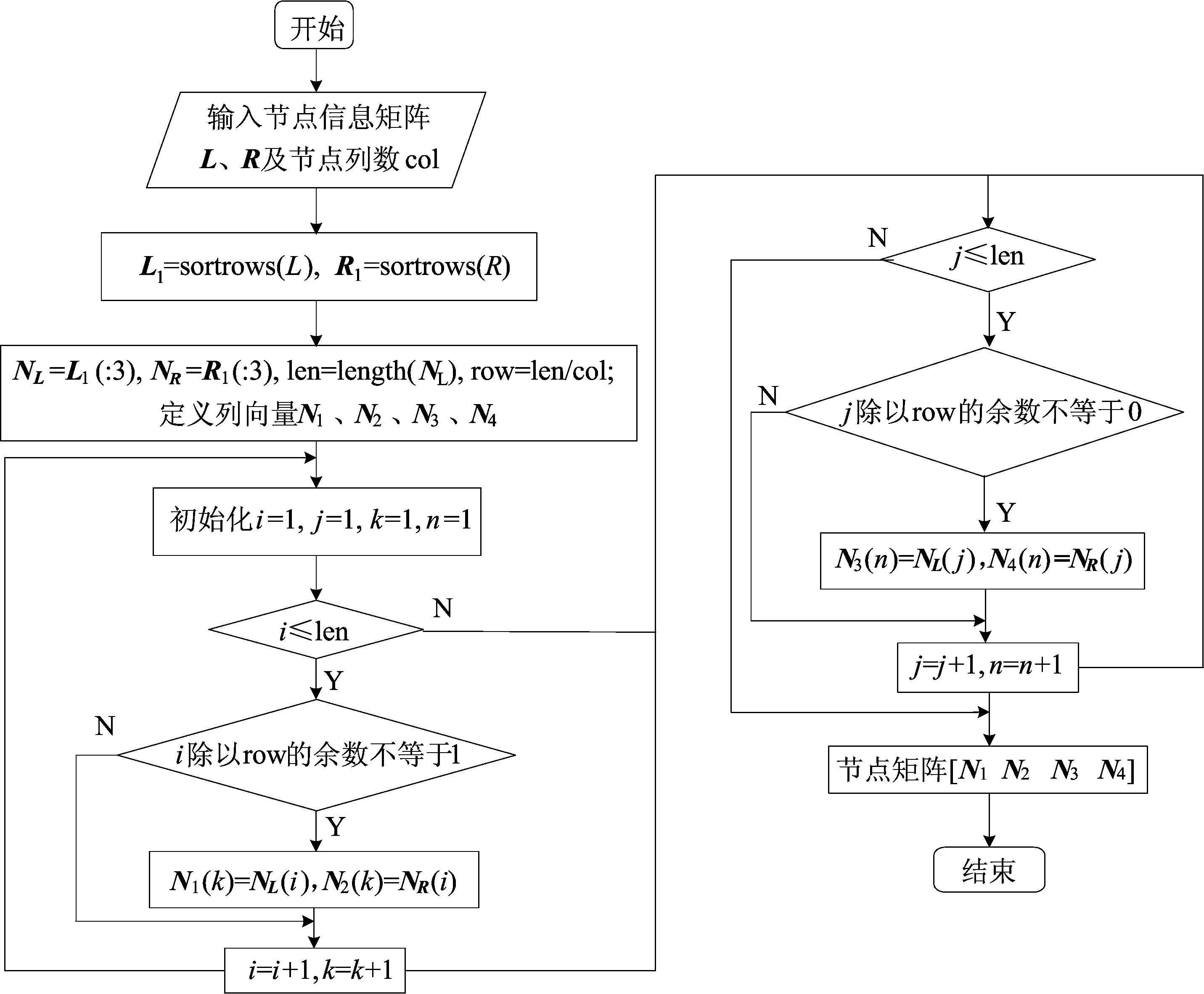
图5 生成自定义单元流程

(3) 将修改后的.inp文件与用户子程序UEL同时导入ABAQUS软件命令行中进行计算，计算结果存储在相应的数据文件中。

该用户子程序UEL是基于VCCT开发的,能够实现裂纹的连续扩展，其基本流程如图6所示。

图6 改进VCCT子程序基本流程

利用有限元软件进行计算,得出裂纹扩展状态,如图7所示。

从图7可以看出,应力集中区域主要在混凝土切缝与沥青层界面过渡区域,随着裂纹的不断扩展,荷载作用一侧应力不断增大。

图7 裂纹扩展应力云图

3.2 应力强度因子计算

利用(1)式将能量释放率转换为应力强度因子,应力强度因子随裂纹扩展的变化规律如图8所示。

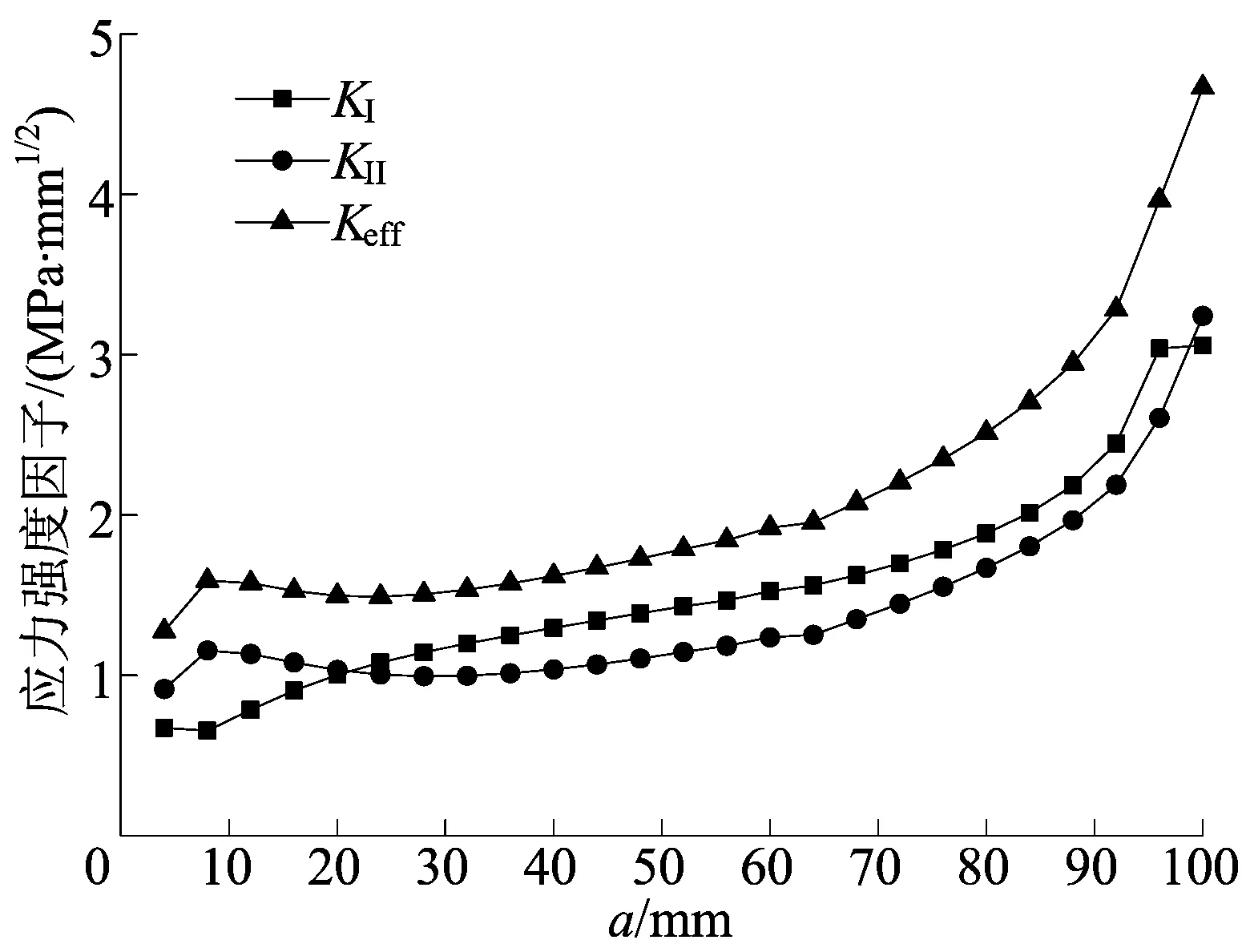
图8 应力强度因子随裂纹扩展的变化曲线

从图8可以看出:KⅠ随着裂纹扩展长度增加而增大;KⅡ先呈递减趋势,然后递增;Keff与KⅡ的变化规律大致相同。应力强度因子下降只存在于下面层,同时,下面层的应力强度因子递增速率要明显小于上面层。

3.3 疲劳寿命计算与分析

根据(6)式,最终疲劳寿命计算结果与网格尺寸da的划分有关,网格划分越细,计算结果越精确。对同一模型划分2种网格尺寸进行计算,当网格尺寸为0.002 5 m时,疲劳寿命为1.51×107次,当网格尺寸为0.002 0 m时,疲劳寿命为1.87×107次,故近似认为尺寸为0.002 5 m的网格已满足精度要求。

通过(6)式计算得出疲劳裂纹扩展寿命,结果如图9所示。

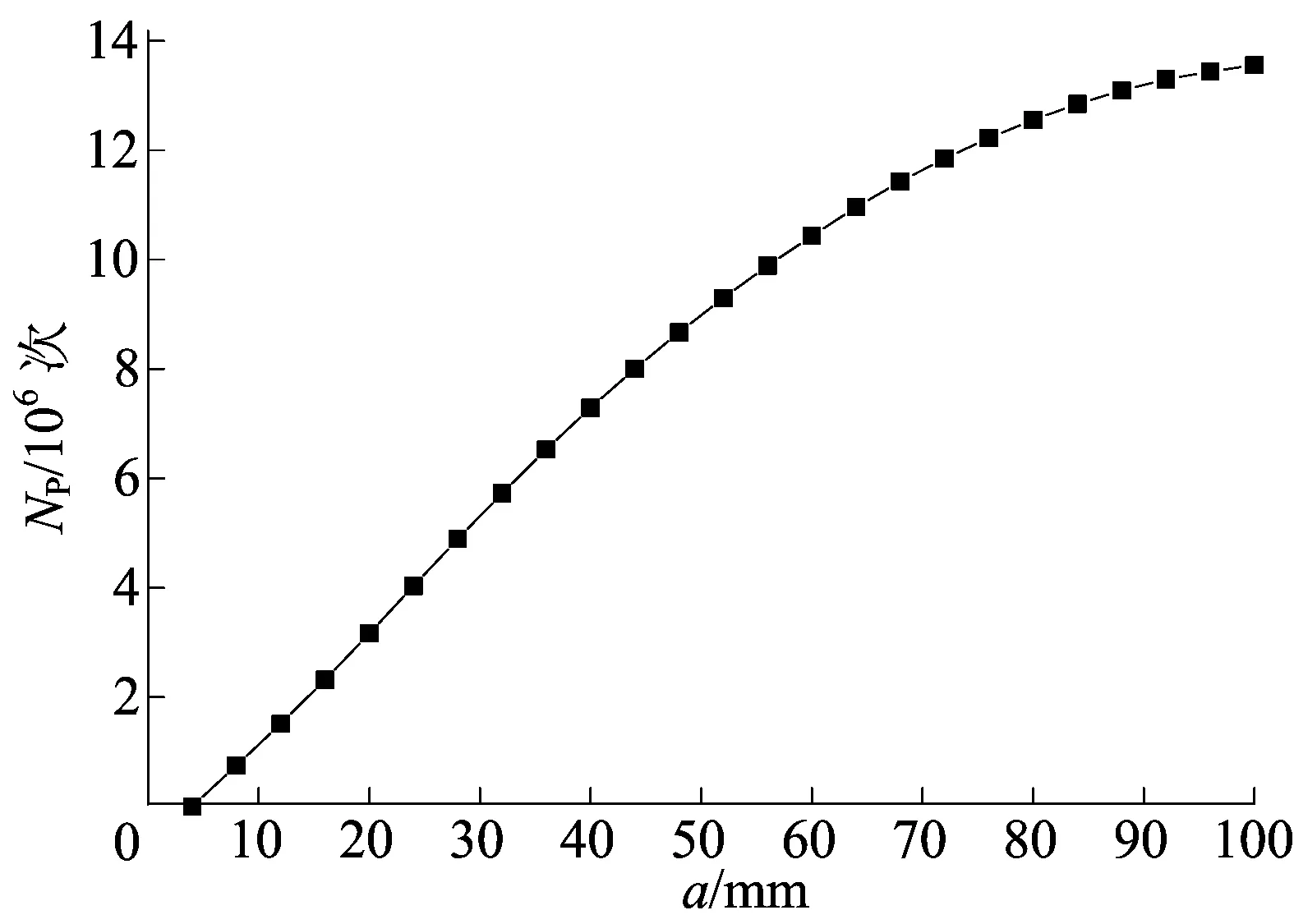
图9 疲劳寿命计算结果

随着荷载的作用次数增加,裂纹长度不断增加,下面层的裂纹扩展速率要小于上面层。当裂纹完全贯穿整个面层时,荷载所作用的次数可视为路面的疲劳裂纹扩展寿命,即为1.37×107次。

文献[25]指出,高级沥青路面一般运营3～5 a后出现反射裂缝。现今国内高速公路平均日交通量标准轴次大约为3 000～60 000次,取3 a运营时间进行计算,路面实际寿命为0.33×107～6.57×107当量轴次,取5 a运营时间进行计算,路面实际寿命为0.56×107～10.95×107当量轴次。本文路面模型的疲劳寿命为1.37×107次,可以看出预估的疲劳寿命大致接近实际寿命。以平均日交通量标准轴次6 000次计算[25],可得运营时间约为6.25 a,故预估的疲劳寿命与实际寿命相比仍然偏大,究其原因，主要有以下3点：① 本文选取的线弹性模型中没有考虑材料的非线性对疲劳寿命的影响，使得结果偏大；② Paris公式中的网格尺寸参数a对计算结果有较大影响，理论上网格尺寸越细计算结果越准确；③ 本文假设当裂纹完全贯穿时的寿命为疲劳寿命，实际情况中裂纹不会完全贯穿，故疲劳寿命的计算结果比实际值偏大。

4 结 论

(1) 本文提出基于VCCT的复合路面疲劳裂纹扩展寿命理论模型,即通过有限元软件结合子程序得到能量释放率,根据所得能量释放率通过理论公式计算得到应力强度因子,再利用相关公式进行裂缝疲劳扩展寿命计算。

(2) 借助有限元软件开发了模拟复合路面疲劳裂纹三维扩展过程的单元,在此基础上编写适用于路面结构开裂的子程序,该子程序模拟裂缝扩展时不需要建立多个模型,而是只需建立1个模型,可高效计算路面结构的能量释放率,减小计算工作量。

(3) 以依托工程中的现场试验路面结构为例,通过本文提出的理论模型计算得到复合路面疲劳裂纹扩展寿命。计算结果表明,疲劳寿命计算值与路面实际的疲劳寿命较为接近,但仍然存在偏差,在实际运用中需对模型进行修正。