基于Udwadia-Kalaba方法的全向移动机器人轨迹跟踪控制

董方方, 金 栋, 赵晓敏, 韩 江

(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

移动机器人是指通过复杂的传感器接收外部环境信息并对自身的状态进行感知,以实现在未知复杂的环境中面向所期望目标的自主运动,完成预定任务的机器人系统。这类机器人具有机动性强、灵活性高等特点,可以适用于劳动强度大、体力要求高、环境恶劣、对人类身体有危害或者是人类无法进入的场所中,代替人类的工作。

目前对移动机器人进行轨迹跟踪控制的主要方法包括鲁棒控制、自适应控制、滑模控制或将多种控制相结合。文献[1]针对三轮移动机器人提出一种结合分层滑模控制与反演控制的控制思路,并以仿真实验验证了其有效性;文献[2]对差速转向移动机器人进行动力学分析,提出一种较为新颖的模糊控制方法,并用联合仿真平台验证该方法的有效性;文献[3]提出一种基于比例积分控制与比例微分控制组合的模糊控制方法，并应用于移动机器人的轨迹跟踪;文献[4]提出一种具有全局渐近稳定的自适应滑模轨迹跟踪控制方法，用于实现轮式移动机器人轨迹跟踪控制。近年来,对于移动机器人的轨迹跟踪控制也有一些新的研究方法,文献[5]运用非线性模型预测控制方法(model predictive control,MPC)对一组两轮平衡小车进行调节控制以及轨迹规划,并用实物实验验证了MPC算法的可行性;文献[6]提出一种粒子群算法规划移动机器人的全局最优位置;文献[7]提出一种基于视觉系统与遗传算法的自适应模糊控制方法,规划两轮移动机器人的最优路径;文献[8]提出一种基于萤火虫算法与比例微分控制的轮式移动机器人最优轨迹控制方法。

Udwadia-kalaba(U-K)方法[9-10]于20世纪90年代提出,是分析力学领域的一个重大突破,它最大的优势在于不引入拉格朗日乘子的情况下,将受到约束的机械系统的约束关系融入到系统的动力学方程中,无论机械系统受到的是理想约束还是非理想约束,都可以通过U-K方程解出约束力的解析表达式。利用U-K方法对机械系统进行轨迹跟踪控制与传统方法的本质区别是传统方法的控制思路多为降低跟踪误差,即对实际轨迹与理想轨迹的偏差量进行控制使其降低,而U-K方法则提供了一种全新的思路,将期望的运动轨迹抽象化为一种虚拟约束,并作为控制力输入以驱动机械系统沿着期望轨迹运动。得益于Udwadia与Kalaba的理论研究,很多学者将U-K方法用于多体系统的动力学分析与控制。文献[11]利用U-K方法对四轮移动机器人进行动力学建模以及跟踪控制,数值仿真结果验证了模型以及轨迹跟踪的正确性;文献[12]基于U-K方程的层级建模方法对三轮移动机器人进行建模,仿真结果验证了轨迹规划的有效性;文献[13]基于U-K基本方程对并联机械手进行动力学建模与轨迹跟踪控制,并且求得各个驱动电机的输出力矩。

本文将U-K方法应用到一种三轮全向移动机器人上。首先建立移动机器人的动力学模型；然后将期望轨迹转化为Pfaffian标准形式施加给机械系统,再通过U-K基本方程得到控制输入的解析解；最后进行数值仿真实验,以跟踪直线与圆形轨迹为例,验证该方法的有效性。

1 动力学模型

三轮全向移动机器人的结构简图如图1所示。3个全向轮的轴线每2条成120°角,而全向轮的中心分布在同一圆上,且轮子轴心指向机器人中心。3个全向轮各由一个直流电机驱动,使机器人既可以沿轮面的切线方向移动,也可以沿轮的轴线方向移动,通过对这2种基本运动方式的组合,可以实现机器人在平面内任意方向的运动。

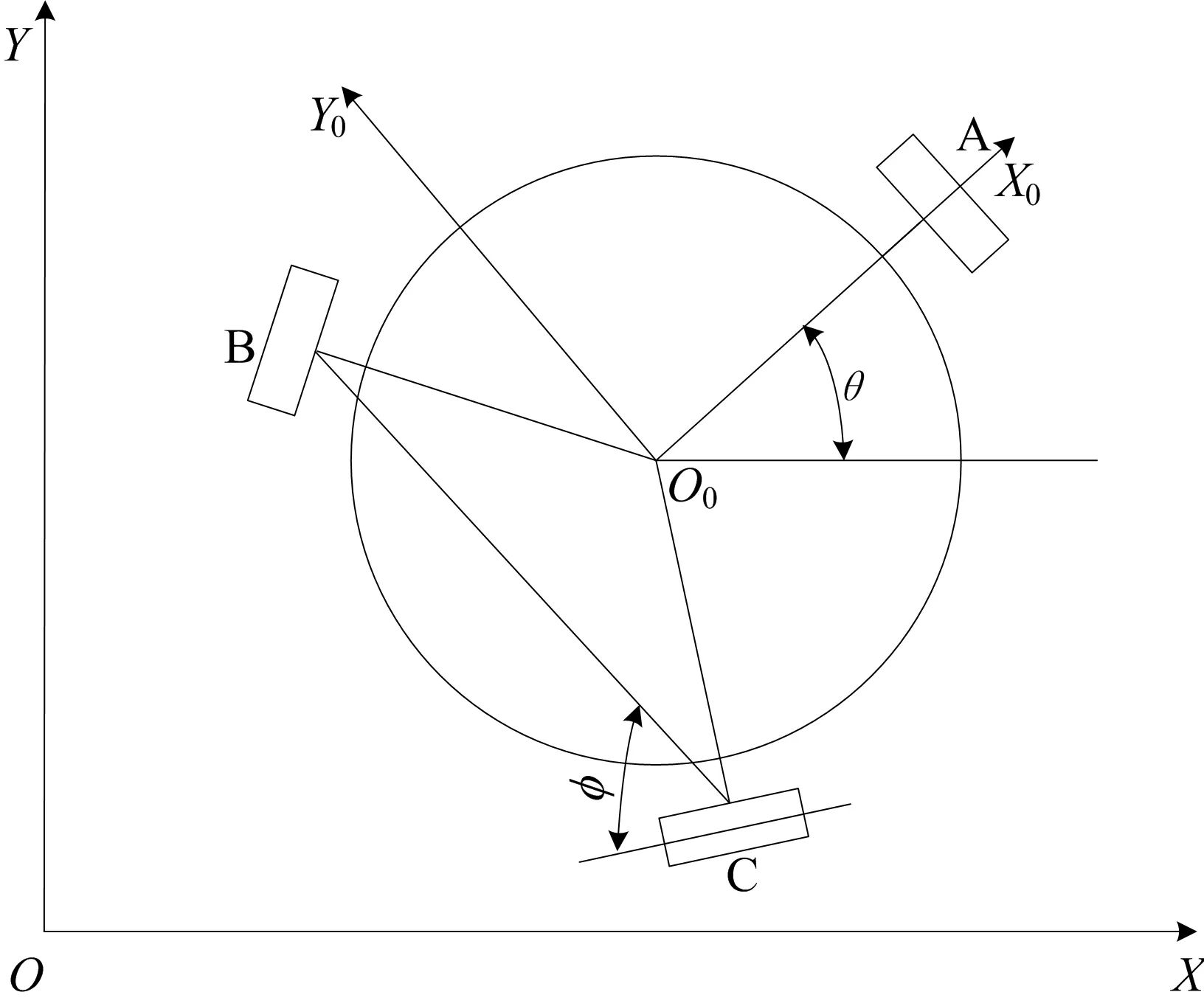
图1 三轮全向移动机器人简图

选取q=[xyθ]T为机器人质心的广义坐标。机器人的各个参数的符号以及定义见表1所列。设逆时针旋转为正,机器人本体坐标系为X0Y0Z0,地坐标系为XOY。在各轮与地面之间为纯滚动的情况下,根据力矩平衡原理,移动机器人加速度力矩为3个轮子力矩的和,即

(1)

表1 机器人各个参数符号及其定义

其中

(2)

将(2)式带入(1)式,可得:

(3)

不同于传统的轮式移动机器人,三轮全向移动机器人的速度方向并不一定垂直于驱动轮的轴线,它的方向是任意的,系统内不存在非完整约束。若要描述机器人速度,则要引入新的参数。因此需要找到机器人运动时加速度的约束关系,根据机器人的结构特性,可以得到其运动时X、Y轴加速度分量与广义坐标之间的关系,具体表示如下:

(4)

将(3)式与(4)式写成矩阵形式,即

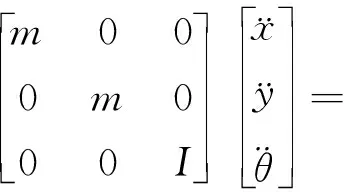
(5)

2 Udwadia-Kalaba方程

U-K方程基本形式的推导过程可以分成以下3个步骤。

(1) 考虑一个无约束的机械系统,假设该系统的广义坐标为q=[q1q2q3…qn]T,则在牛顿力学或者拉格朗日力学中,该系统的运动学方程可以表达为:

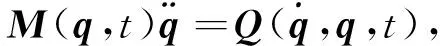
(6)

(2) 引入系统中应该被考虑的约束因素,假设系统受到h个完整约束,其形式为:

φi(q,t)=0,i=1,2,…,h

(7)

受到k-h个非完整约束的形式为:

(8)

二阶约束是进一步进行动力学分析和控制设计的最合适形式。使用二阶约束的优点在于它的加速度是线性的,而且满足零阶或一阶初始条件的信息仍然被保留在二阶约束方程的初始条件中。在假设约束方程充分光滑的前提下,对完整约束方程求导2次,对非完整约束方程求导1次可以得到约束方程的二阶形式,即

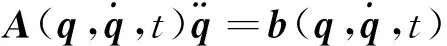
(9)

(3) 给系统引入一系列的外部约束,此时的机械系统变为“受约束系统”。因此,约束系统的实际显式运动方程可以表述为:

(10)

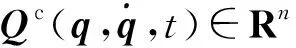
Qc=M1/2B+(b-AM-1Q)

(11)

其中,B=AM-1/2,B+表示B的Moore-Penrose(M-P)广义逆矩阵。M-P广义逆矩阵在描述约束运动的过程中起着重要作用,假设矩阵A的M-P逆矩阵为A+，那么A+满足以下条件:

AA+A=A,

A+AA+=A+,

AA+=(AA+)T,

A+A=(A+A)T

(12)

由(10)式和(11)式,受到约束的机械系统的显式运动方程可以表达为：

(13)

至此得到U-K方程的基本形式,可见其不依赖于额外的辅助变量求解。

3 轨迹跟踪控制

在得到无额外约束下的系统动力学方程后,为了使移动机器人沿着期望的轨迹运动,需要施加额外的约束力。从U-K方法的观点出发,将所需要跟踪的位置或速度轨迹抽象成虚拟的约束,然后将该约束转化为Pfaffian标准形式,再利用U-K方程获得系统满足该轨迹约束所需要的驱动力矩,从而实现机器人的轨迹跟踪控制。

假设现在期望机器人质心的X轴坐标和Y轴坐标分别为时间t的函数fX(t)和fY(t),即

(14)

将(14)式对时间t求二次导,将其写成二阶约束的形式,即

(15)

(16)

其中

至此,求出移动机器人要满足期望轨迹曲线时所需的驱动力矩。

4 数值仿真分析

本节将用数值仿真分析来验证第1节与第3节中动力学模型与轨迹跟踪控制方法的正确性。在以下2个示例中,将求解3个全向轮的控制力矩,使机器人沿着期望轨迹运动,采用Matlab的ode15i算法求解U-K方程。

4.1 期望的跟踪轨迹

假设机器人运动满足以下具体的轨迹方程:

(17)

易知这个关于时间t的参数方程合成的复合运动轨迹为垂直于Y轴的往复直线运动,将(17)式对时间t求二次导可得:

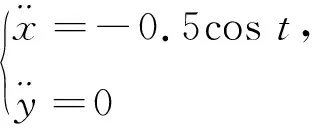
(18)

并给定初始条件为:

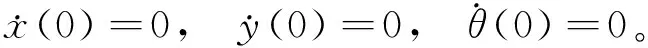
同理,若期望移动机器人运动轨迹为圆形,则机器人运动满足以下轨迹方程:

(19)

将(19)式对时间t求二次导可得:

(20)

给定初始条件为:

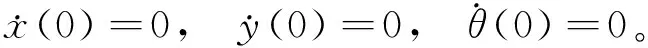
数值仿真中需要用到的机器人参数见表2所列。

表2 移动机器人参数

4.2 数值仿真结果

4.1节中所述的往复直线机器人运动轨迹以及机器人中心点在X、Y轴的理想轨迹与实际轨迹如图2所示。质心点在两轴的轨迹分别为fX(t)=0.5cost、fY(t)=3。

图2 直线运动轨迹及各轴运动轨迹

根据(11)式可以求出满足理想轨迹所需的驱动力矩,移动机器人运动轨迹为直线时各个全向驱动轮的输出力矩如图3所示。

图3 直线轨迹下各轮输出力矩

机器人运动轨迹为直线时X、Y轴的轨迹跟踪误差为x-fX(t)、y-fY(t),如图4所示。

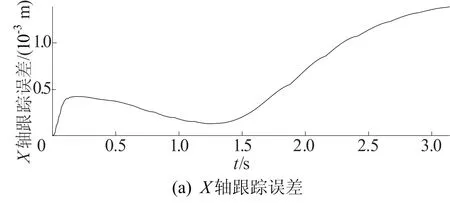
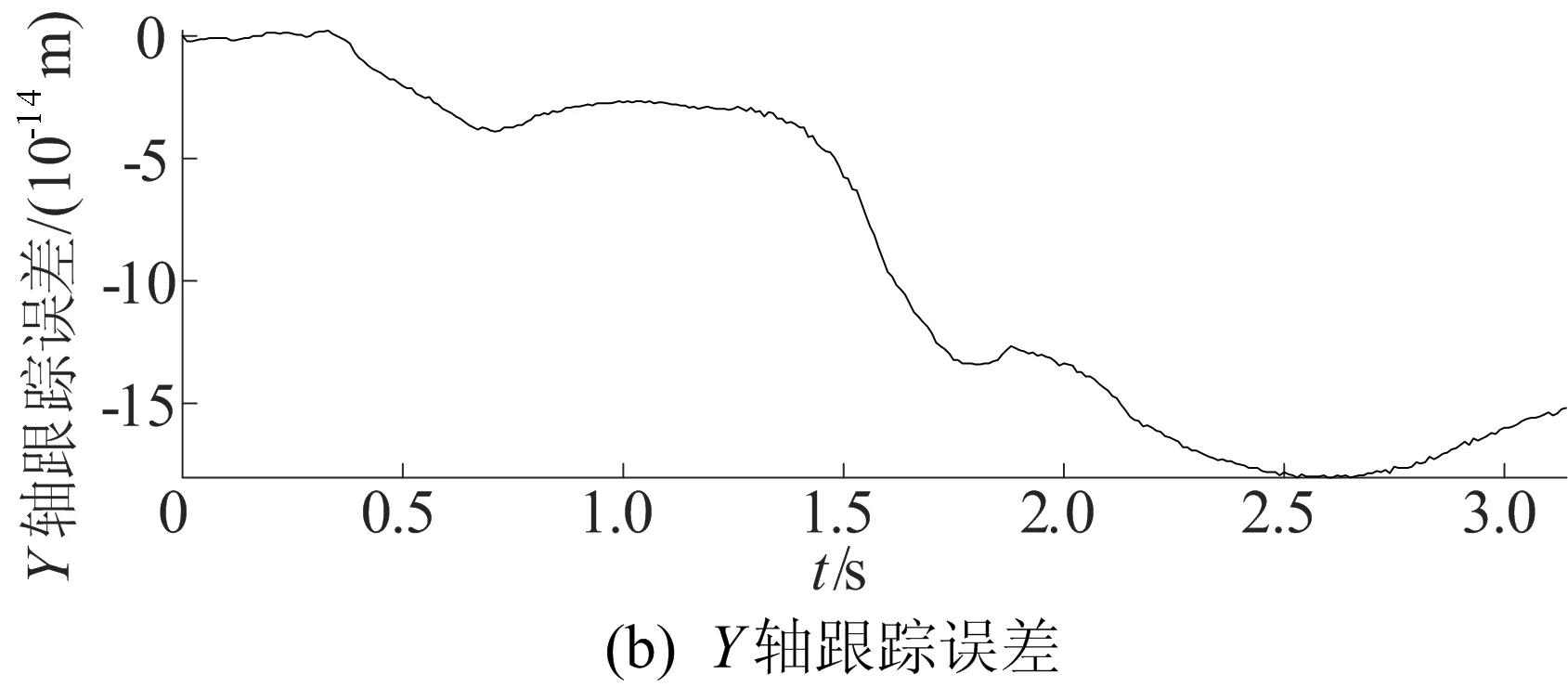
图4 直线轨迹下各轴跟踪误差

从图4可以看出,应用U-K方法规划移动机器人轨迹时误差较小。这充分说明了U-K方法的准确性。

4.1节所述的圆弧运动轨迹如图5所示,机器人质心点在两坐标轴上的运动轨迹分别为:

fX(t)=0.5sint2,

fY(t)=0.5cost2。

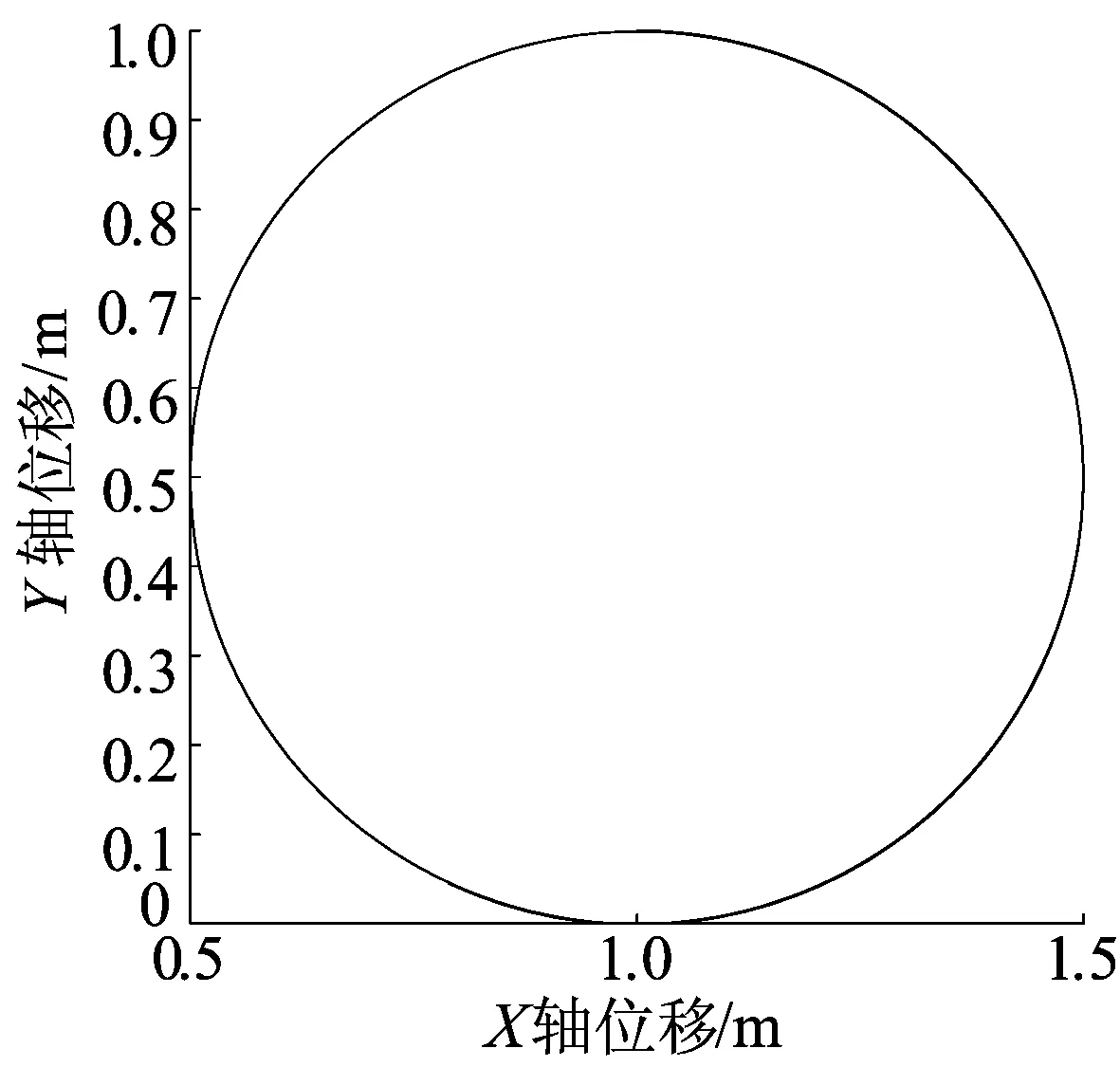
图5 圆形运动轨迹

X、Y两轴的理想运动轨迹和实际运动轨迹如图6所示。从图6可以看出,2种轨迹基本重合。

图6 圆形运动轨迹下各轴轨迹

同理可以求出机器人运动轨迹为圆形时各个全向轮的输出力矩,如图7所示。

图7 圆形轨迹下各轮输出力矩

圆形轨迹时各轴的轨迹跟踪误差如图8所示。从图8可以看出,各轴的跟踪误差达到了10-4量级,误差较小。

图8 圆形轨迹下各轴跟踪误差

从以上仿真结果来看,无论是跟踪直线轨迹还是圆形轨迹,运用U-K方法对移动机器人的轨迹进行规划后,所得的运动轨迹都能很好地满足期望运动轨迹,同时也表明了本文建模的正确性以及U-K方法的准确性与可靠性。

5 结 论

本文针对三轮全向移动平台提出了一种基于U-K方法的轨迹跟踪控制思路。首先将系统视为无约束系统,再将运动轨迹抽象化为虚拟约束施加在机械系统上,由U-K方程求出满足轨迹约束时所需要的驱动力矩。本文以数值仿真的形式验证了U-K方法的正确性与可靠性。此外,本文所提出的轨迹跟踪控制方法具有可迁移性,在理想情况下,无论是全向移动机器人还是欠驱动移动机器人,或是更为复杂的机械系统,该方法都能进行高精度轨迹跟踪控制。但实际应用中系统的不确定性以及不可避免的外界干扰都会导致控制精度的降低，且随着系统自由度的增加,系统动力学解析表达式计算出来的矩阵会十分复杂,计算时间变长,因此满足系统实时控制还存在一定问题，有待进一步研究。