沥青混合料动态模量试验的仿真和验证
袁 淼, 韩 丁, 李 阳, 杜庆灿
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
沥青混合料是常见的道路建筑用材料,可以认为是由沥青砂浆、骨料、孔隙和界面(interface transition zone,ITZ)组成的多相体材料[1-2]。许多研究者对基于图像处理技术的建模方法进行了研究。文献[1]应用数字图像处理技术识别水泥乳化沥青混合料(cement-emulsified asphalt concrete,CEAC)的三相材料,在局部区域建立了二维细观有限元子模型;文献[3]利用数字图像处理技术深入分析了沥青混合料主骨架在荷载作用下的渐进细观结构响应特性;文献[4]利用数字图像处理技术,对沥青混合料主骨架、接触链的统计特性及其在荷载作用下的渐进行为进行了研究分析;文献[5]采用数字图像处理技术,表征了不同压实周期下沥青混合料的骨架特征,从宏细观角度分析了沥青混合料在压实过程中集料骨架的变化。
无论是连续介质还是离散元细观模型都常采用参数化建模的方法。文献[6]提出一种改进的数值方法生成类混凝土颗粒增强复合材料的三维细观模型;文献[7]基于图像处理技术和参数化建模的方法,生成不同集料空间分布和体积分数的有限元模型;文献[8-9]采用离散单元法(discrete element method,DEM)研究和分析了集料的结构和功能,并利用颗粒流三维(particle flow 3D, PEC3D)DEM程序进行数值模拟。
建立沥青混合料的细观模型时,合理选择骨料的几何形态至关重要。文献[10]以椭圆为基准,引入旋转坐标生成多边形骨料,并直接以多边形骨料本身为目标进行交涉判定;文献[11]利用图像处理技术获取骨料的截面轮廓,识别轮廓特征后通过改进的分形布朗运动(fractional Brownian movement,FBM)法生成随机的数值骨料截面轮廓。
在已有的研究中,应用参数化建模的方法建立骨料的细观模型时,骨料的棱角形态越复杂,骨料的尺寸大小就越难以控制,随机生成的骨料难以同时兼顾两者。本文基于分形维数指标,可控制生成具有合理棱角形态和尺寸大小的骨料截面,再综合数值图像法和参数化建模的方法,生成了沥青混合料的细观虚拟试件,建立单轴压缩动态模量试验模型,并进行了分析和验证。
1 骨料截面的几何形态
要建立合理的虚拟骨料截面,需要对真实骨料截面的形态特征进行统计学分析。本文通过分析真实骨料截面的形态特征,基于分形维数和中点位移法对骨料的截面轮廓进行重构。
1.1 骨料截面轮廓的分形特征
分形维数D可以通过盒维数法进行测定。先将骨料截面轮廓进行不同边长的正方形网格划分,记录不同网格边长和轮廓包含的网格数量,分形维数D的计算公式[12]为:
(1)
其中:Nr为骨料截面轮廓包含的网格数量;r为网格边长。
标准马歇尔试件的横向剖切面如图1所示,基于图形处理技术提取各骨料截面轮廓,并计算得到分形维数的样本数据。将样本数据绘制成分形维数占比的直方图,如图2所示,结果表明骨料截面轮廓的分形维数符合正态分布,其均值为1.158,标准差为0.057 6。

图1 试件剖面图

图2 骨料分形维数分布
1.2 骨料截面轮廓的重构
需研究如何基于分形维数重构骨料的截面轮廓。文献[13]研究了城市形态学的分形特征,并用中点位移法模拟了城市边界,在基准图形上生成不规则折线。本文基于基准图形,结合分形维数和中点位移法来重构骨料截面轮廓。分形维数D与偏移角α的关系如下:
(2)
由(2)式可知,偏移角度数随分形维数而变化,在基准边上生长1次的示意图如图3所示。
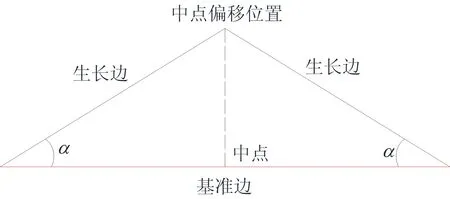
图3 中点位移法示意图
本文选取的基准图形为正方形,通过中点位移法在基准图形各边上生成骨料截面轮廓,会产生面积增量。设正方形的面积为S0,边长为d,面积增量ΔS的计算公式为:

(3)
定义放大系数γ,其计算公式为:
(4)
其中,Si为重构的第i档骨料截面面积。
由(2)~(4)式可得放大系数γ和分形维数D的关系如下:
(5)
若Si已知,则重构骨料截面的步骤如下:
(1) 根据骨料分形维数的正态分布随机选择分形维数D。
(2) 由D和(5)式可得放大系数γ。
(3) 由γ、已知Si和(4)式可得基准正方形的面积S0及其边长d。
(4) 由D和(2)式可得偏移角α。
(5) 将基准正方形绕质心随机旋转一个角度,再依据α对各边分别进行1次中点位移,可得重构的骨料截面,且其面积为Si。
2 单轴压缩动态模量试验的建模
沥青混合料的动态模量是进行沥青路面设计和路面结构验算的重要参数。我国沥青混合料单轴压缩动态模量试验(T 0738—2011)的试件尺寸[14]为φ100 mm×150 mm。为了简化计算,可以采用柱坐标系来简化圆柱形沥青混合料试件,即采用尺寸为 50 mm×150 mm的二维试件。
2.1 骨料截面库和骨料级配
重构骨料截面轮廓需要骨料截面面积已知,本文选择上下相邻两筛孔面积的均值作为该档骨料截面面积Si,按照骨料重构步骤建立各档骨料同面积、不同截面的骨料截面库。
为获取二维尺度上的骨料级配曲线,借助瓦拉文(Walraven)公式,基于Fuller级配公式将三维上的骨料级配曲线转化为二维上各档骨料截面级配的概率分布Pi[15]为:
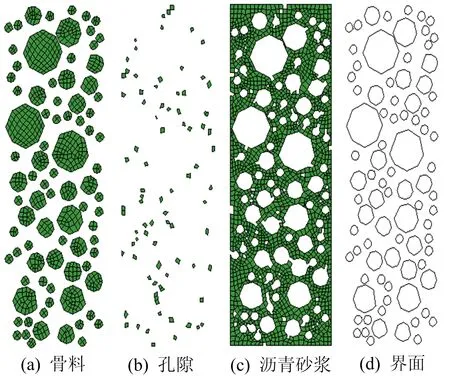
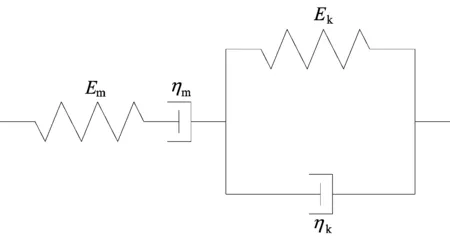
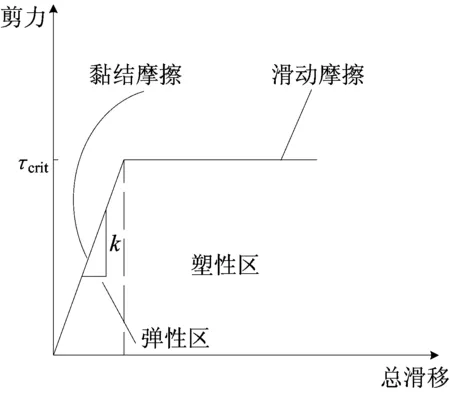
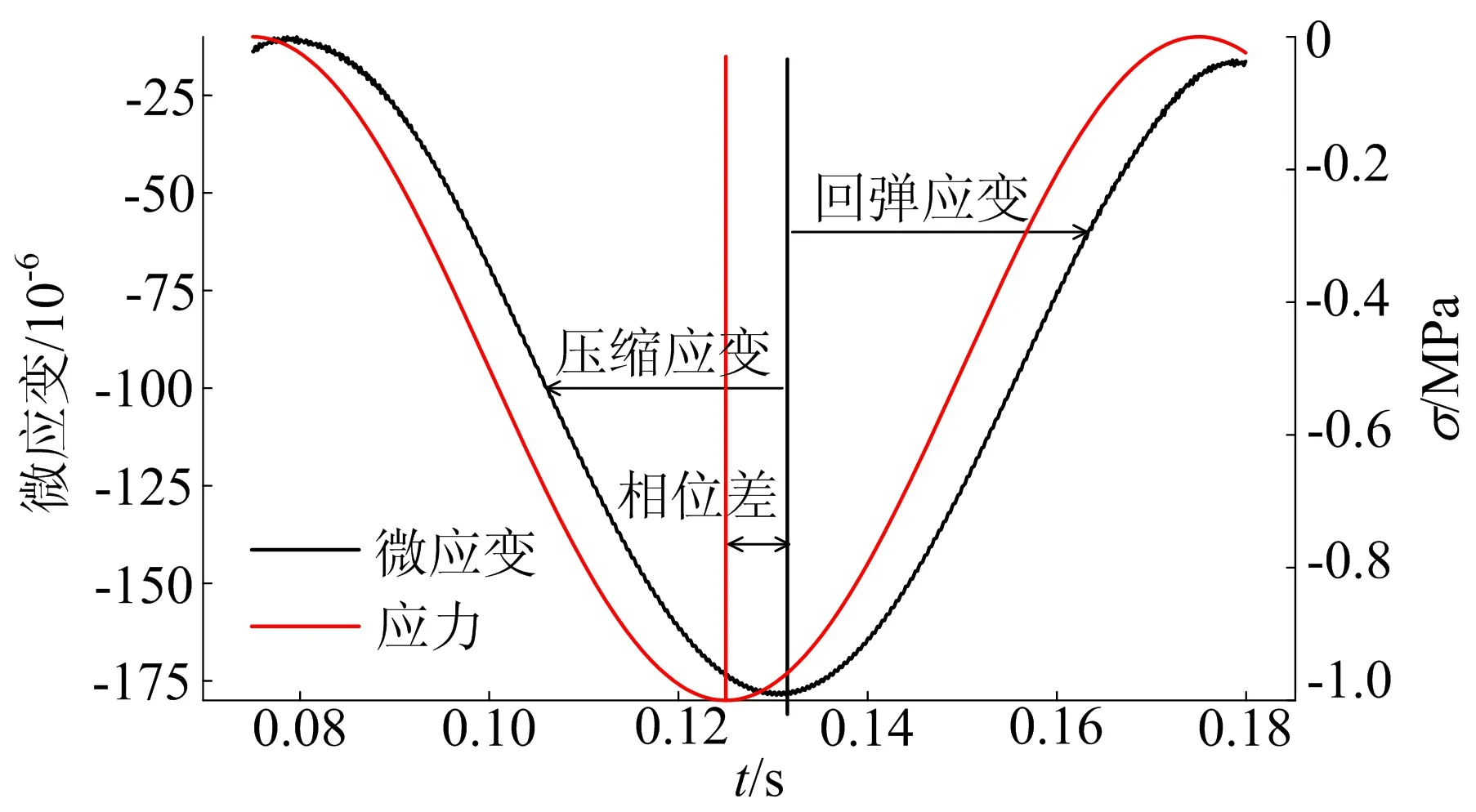
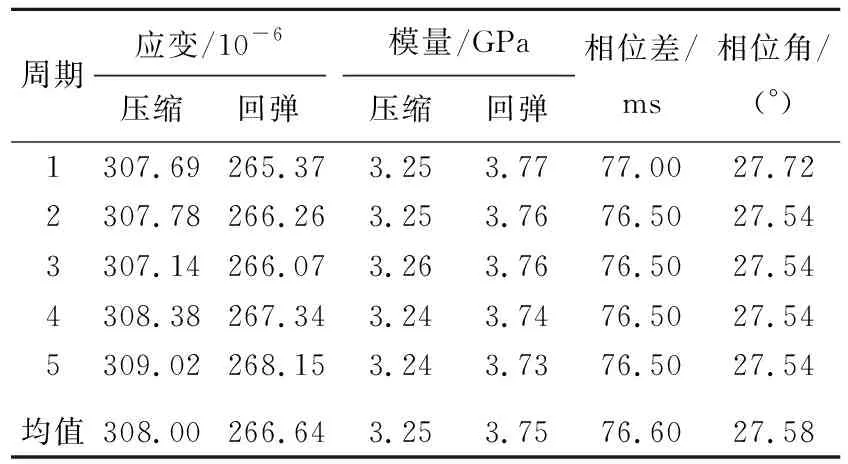
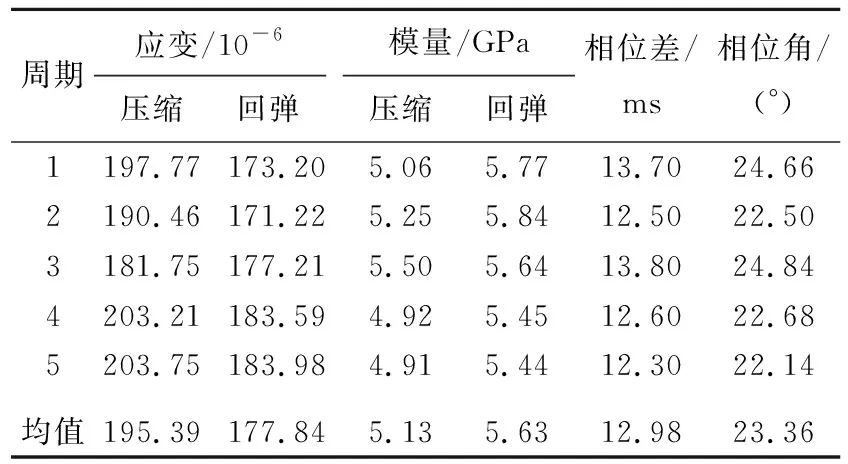
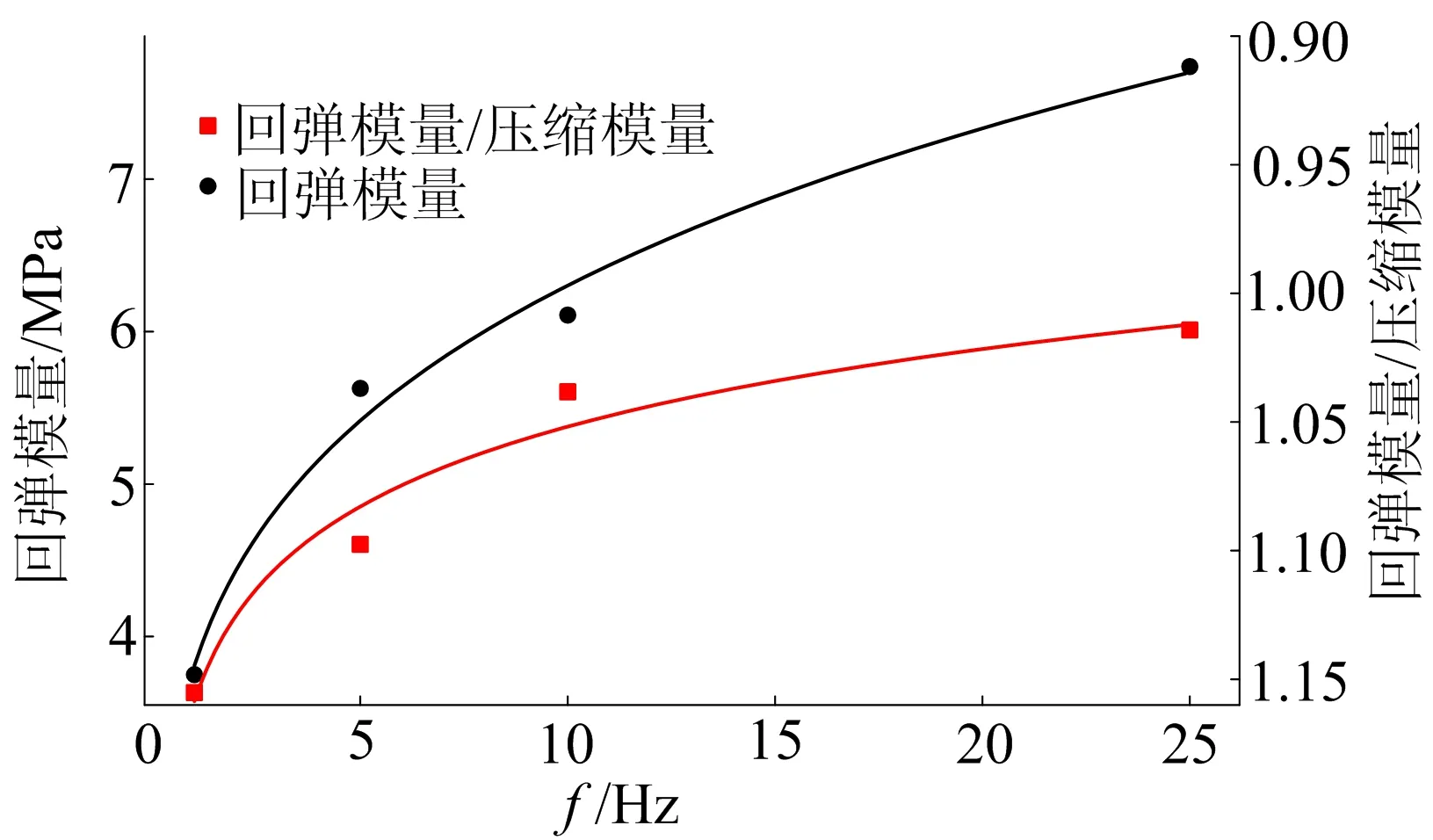
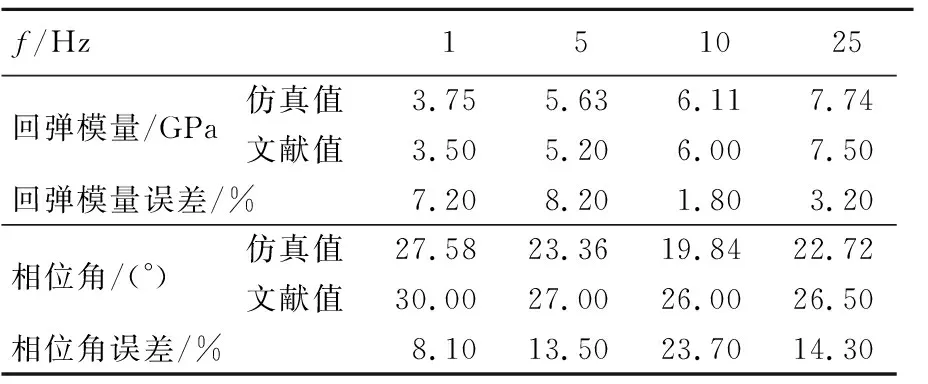
Pi(D 0.053(D0/Dmax)4-0.012(D0/Dmax)6- 0.004 5(D0/Dmax)8-0.002 5(D0/Dmax)10] (6) 其中:D0为方形筛孔的尺寸;Dmax为最大骨料粒径;φk为骨料体积分数(包括粗骨料和细骨料)。 将沥青和2.36 mm及以下的骨料作为沥青砂浆。已知Si,所需的各档骨料截面的数目计算公式如下: ni=(Pi+1-Pi)S/Si (7) 其中:S为二维试件的面积;ni为第i档骨料截面的数目。各档骨料截面的数目见表1所列。 表1 各档骨料截面的数目 本文建立的50 mm×150 mm沥青混合料虚拟试件是由骨料、孔隙、沥青砂浆和界面组成的四相体材料。本文虚拟试件建模步骤如下: (1) 骨料模型。由瓦拉文公式计算得到的骨料截面的级配,建立各档粒径的骨料截面库,抽取所需的骨料截面数目ni,根据随机投放算法完成所有骨料截面的投放;分别识别各骨料截面的角点坐标,将坐标导入ABAQUS中生成骨料集合,校核本文的骨料面积占比为49.03%。 (2) 沥青砂浆和孔隙模型。骨料投放完成后,数值试件的剩余空间包含孔隙和沥青砂浆;在ABAQUS中对剩余空间进行网格划分,抽取一定数量的网格单元作为孔隙,直至达到相应的孔隙率,本文孔隙率[16]取4%。 (3) 界面模型。在ABAQUS中采用接触对定义骨料和沥青砂浆的界面,并将骨料作为接触对的主面。 沥青混合料虚拟试件的各相组成如图4所示。 图4 虚拟试件的各相组成 考虑到柱坐标系的设定,在虚拟试件的底部和内侧均施加法向约束。为使虚拟试件顶部均匀受力,设置尺寸为60 mm×20 mm的铁板压头,弹性模量为210 GPa,泊松比为0.15。铁板内侧也施加法向约束,在铁板顶部施加相应的动态荷载。 虚拟试件各细观相材料采用不同的本构模型,其中骨料采用弹性本构模型,沥青砂浆采用黏弹性本构模型,界面采用接触模型。 美国国家公路与运输协会(American Association of State Highway and Transportation Officials,AASHTO)的TP-62 03对变形类指标采用了21.1 ℃的试验温度;我国沥青混合料单轴压缩动态模量试验(T 0738—2011)(以下简称《试验规程》)对变形类指标推荐采用20 ℃的试验温度,控温准确度[14]为±0.5 ℃。因此,本文选取21 ℃时4种加载频率下沥青砂浆的Burgers模型如图5所示,参数[17]见表2所列。 图5 Burgers模型示意图 表2 Burgers模型参数 为了便于计算,将沥青砂浆的Burgers模型参数转换成二阶的Prony级数形式,具体公式如下: G(t)=G∞+G0(g1e-t/τ1+g2e-t/τ2) (8) 其中,G∞=0;G0=Em/[2(1+ν)];τ1=1/α; Burgers模型的Prony级数参数见表3所列。 表3 Burgers模型的Prony级数参数 骨料类型为玄武岩,弹性模量为40 GPa,泊松比[18]为0.2。界面的接触模型采用弹性滑移模型,如图6所示,剪切牵引斜率[19]k取300 kN/m。 图6 弹性滑移的接触模型 按《试验规程》的规定,在铁板顶部施加峰值为1 MPa的偏移正弦波均布压力荷载,加载频率[17]分别为1、5、10、25 Hz。以10 Hz作用下的单次加载周期为例,试件顶面的垂直压应力与试件轴向平均压应变的时程曲线如图7所示。 图7 应力-应变时程曲线 因为动态模量和相位角是试验的目标结果,所以将压缩应变、回弹应变和相位差作为计算指标。对4种加载频率各选用5个加载周期作为荷载输入。各计算指标的仿真试验数据见表4~表7所列。 表4 加载频率1 Hz仿真数据 表5 加载频率5 Hz仿真数据 表6 加载频率10 Hz仿真数据 表7 加载频率25 Hz仿真数据 《试验规程》中沥青混合料动态模量的计算公式为: (9) 其中:|E*|为沥青混合料的动态模量;σ为轴向应力幅值;ε为轴向应变幅值。 《试验规程》采用可恢复轴向变形平均幅值计算轴向应变幅值。为了分析压缩和回弹过程导致的动态弹性模量的差异,轴向应变幅值分别采用压缩应变幅值和回弹应变幅值,各频率下的计算结果见表4~表7所列,仿真数据回归分析结果如图8所示。 图8 仿真数据回归分析 由拟合得到的回弹模量均值Et与频率f的曲线可知Et具有频率依赖性,且具有非线性的特征。Et与f的相关系数为0.935 6,Et的拟合公式为: Et=3.81f0.22 (10) 由拟合得到的回弹模量均值与压缩模量均值的比值Et/Ec与频率f的曲线可以看出,回弹模量要大于压缩模量,但随着频率的增加,两者逐渐接近。《试验规程》采用可恢复轴向变形进行计算,本质上是回弹模量。Et/Ec与f的相关系数为-0.878 1,Et/Ec的拟合公式为: (11) 《试验规程》中沥青混合料相位角的计算公式为: (12) 其中:φi、ti分别为第i次加载周期时的应变峰值与应力峰值的相位角和相位差;Ti为第i个加载周期。各频率下的计算结果见表4~表7所列。 将4种加载频率下的回弹模量和相位角的均值与文献[17]的试验数据进行比较,结果见表8所列。 表8 仿真数据与文献数据的对比 从表8可以看出,通过仿真试验数据计算得到的动态回弹模量与基于试验数据获得的动态模量较为吻合,这表明本文的细观虚拟试验模型具有较好的实用性。但是,相位角的误差相对较大,原因是试验数据本身在10 Hz处最小,可能存在变异。 (1) 基于图像处理技术对骨料截面轮廓的分形特征进行识别,发现其符合正态分布规律。以正方形为基准图形,建立了采用分形维数和中点位移法重构骨料截面轮廓的方法。 (2) 基于柱坐标系的特征,将圆柱形沥青混合料马歇尔试件简化为二维试件。基于瓦拉文公式和骨料的Fuller级配曲线,获得了二维试件上所需投放的各档骨料截面数目。建立四相体的沥青混合料数值试件,其中沥青砂浆材料采用不同频率下的黏弹性本构模型。 (3) 基于试验数据对单轴压缩动态模量仿真试验的计算结果进行了对比分析,结果表明,本文建立的细观虚拟试验具有较好的实用性。此外,研究还发现基于回弹变形的动态模量要大于基于压缩变形的动态模量,但随着频率的增加,两者逐渐接近。与动态回弹模量相比,相位角的仿真计算结果与试验数据的偏差稍大,表明后续应进一步研究加载频率对沥青基材料黏弹性特征的影响。
2.2 虚拟试件建模
2.3 仿真试验的设置
3 细观相材料的本构模型

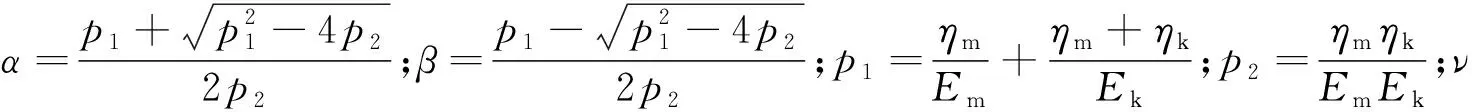

4 仿真试验的分析与验证
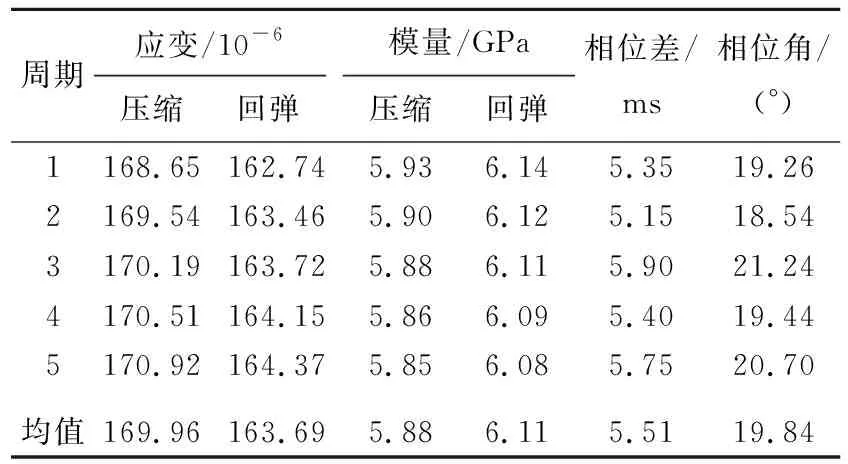
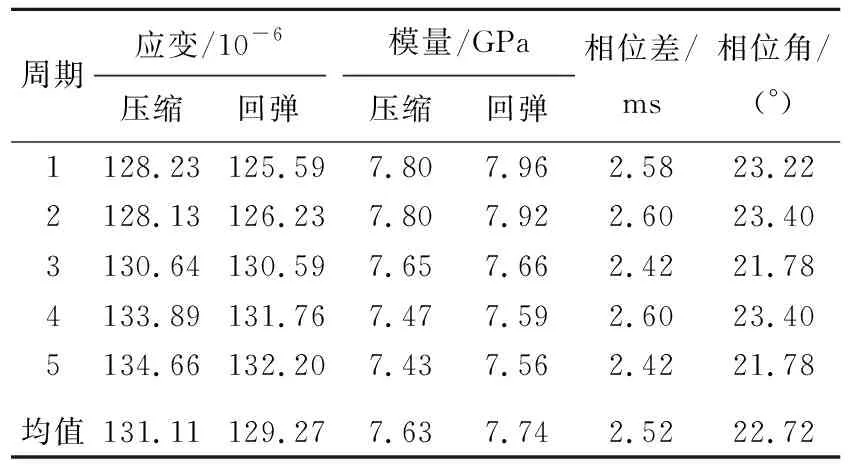
4.1 动态弹性模量
4.2 相位角
4.3 仿真试验结果的验证
5 结 论

