借助好题提高学生数学综合能力浅探
王培幼
借助好题提高学生数学综合能力浅探
王培幼
(宁波市奉化居敬小学,浙江宁波315502)
《义务教育教学课程标准(2011版)》指出:数学评价既要关注学生知识与技能的理解和掌握,更要关注他们情感的形成和发展;既要关注学生数学学习的结果与成效,更要关注他们学习过程中的变化和发展。为了落实新课标的评价理念,许多好题应运而生,教师应走出让学生重复练习的怪圈,搜集好题、读懂好题、用透好题,让学生在好题的练习和熏陶下,知识和能力得到提升。
过程理解;核心素养;综合能力
数学习题是教学中的重要组成部分。好的习题,不仅可以加深学生对知识的理解,更有助于发展他们的各种能力,切实培养学生的核心素养。
一、好题,基于真实情境
好题跳出了纯粹数学的思维框架,把数学知识和数学技能置于“身边数学”的现实情境中,能培养学生的数学应用意识和解决实际问题的能力。
好题1:

图1
一个用塑料薄膜制作的蔬菜大棚,长20米,横截面是一个半径为2米的半圆形,如图1所示。
(1)这个大棚的占地面积是多少平方米?
(2)搭建这个大棚至少要用塑料薄膜多少平方米?
(3)大棚内的空间有多大?
赏析:弗赖登塔尔认为,数学学习需要学生完成两次转换:首先要将现实问题转化成数学问题,实现第一次转换;再建立数学问题与数学形式系统之间的关系,实现第二次转换。求大棚的占地面积就是求圆柱沿着底面直径的纵剖面面积,搭建大棚至少要用的塑料薄膜就是求圆柱表面积的一半,大棚内的空间大小就是求圆柱体积的一半。虽然三小题用到的都是圆柱中的基本知识,但这样贴近真实情境的题比起单纯的几何题对学生更具挑战,学生只有明确了问题所指,才能完成从现实问题到数学问题的转换,继而收集有效信息,利用公式求解。
二、好题,重视过程理解
好题应该做到过程与结果并重,在解题过程中能够使知识的探索发现过程再现出来,再一次经历知识形成过程,培养学生的探究意识和探究能力。
好题2:
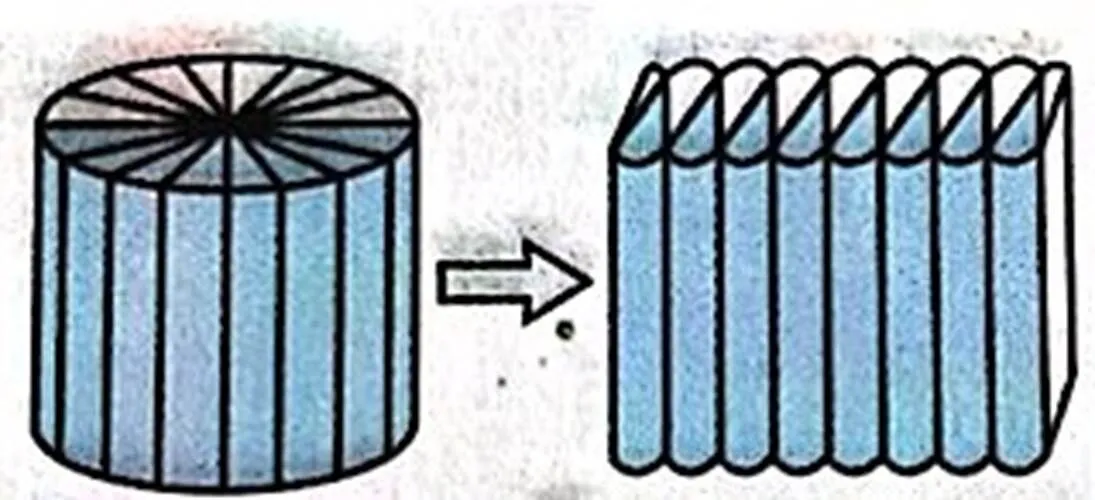
图2
小明在解决“已知圆柱的底面直径为6cm,高8cm,求这个圆柱的体积。”这一问题的时候,没有直接用体积公式进行计算,而是根据圆柱体体积计算公式的推导过程,想出了一种别出心裁的方法,分步计算圆柱的体积(如图2所示)。能看懂他的方法吗?请补上小明的最后一步(第三步)算式,计算出圆柱体的体积。
第一步:3.14×6÷2=9.42cm
第二步:6÷2=3cm
第三步:_______________
请你借助右图说说小明这样做的理由:_______。
赏析:在教学中既要重视结果,更要重视知识的获得过程,在考查中,同样应重视对知识获得过程的理解。计算圆柱体积不难,本题将学生的思路引向圆柱体体积计算公式的推导过程,学生想要补上小明的第三步必须先看懂前两步。通过这样的考查形式,能充分掌握学生学习新课时的状态,检测是否经历过圆柱体体积计算公式推导过程,是否理解这一过程。
三、好题,关注核心素养
对学生核心素养的培养不仅体现在课堂上,也可以体现在习题中。好题可以将培养学生的推理思想、几何直观、化归思想、转化思想、数感、空间观念等数学素养融入其中,使学生在做题过程中发展各种能力。
好题3:
用8块相同的长方形地砖拼成一块长方形地面,地面周长为300厘米,地砖的拼放方式如图3所示,试求每块地砖的宽。

图3
赏析:此题可以培养学生的推理能力。根据给出的信息“周长300厘米”,学生需要找到长方形地面的周长是由五条长五条宽组成的,因为长宽数量相同,所以可以将周长平均分成五份得到一组长宽的和是60厘米。通过进一步观察,学生需要推理出一条长相当于三条宽,因此可以将长宽的和用四条宽代替,从而求出每块地砖的宽。在整个解题过程中,学生需要经历不断地观察、对比、分析、推理的过程,能切实培养学生的核心素养。
好题4:
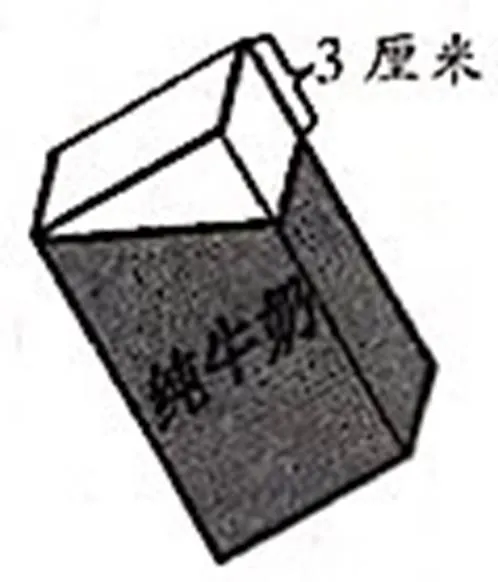
图4
一个长6厘米,宽4厘米,高12厘米的长方体牛奶盒,装满牛奶。笑笑在准备喝牛奶时一不小心把盒子弄歪了,洒出一些牛奶,也就是图中的空白部分。洒出()毫升牛奶,如图4所示。
赏析:空白部分是一个三棱柱,虽然教材没有出现三棱柱体积计算方法,但是在以往的学习过程中,一部分学生已经积累了丰富的学习经验,通过长方体、正方体、圆柱等直棱柱体积都可以用“底面积×高”计算,他们已经能够根据三棱柱的特征推理出也可以用同样的方法计算体积,这对学生来说是一个展示的机会。本题也可以利用“转化”的思想,将空白部分×2,把三棱柱转化为长方体,这样就能利用旧知求出新知。推理能力的培养和转化思想的渗透都是培养学生核心素养的落脚点。
四、好题,发展综合能力
学生对于单项知识的题解决起来不难,但把会解决的几个单项题综合起呈现在同一题中就会感到困难,他们无法识别或调用需要用到的知识,使解题陷入一片混沌。因此,为学生设置进行综合能力训练的题很有必要。
好题5:
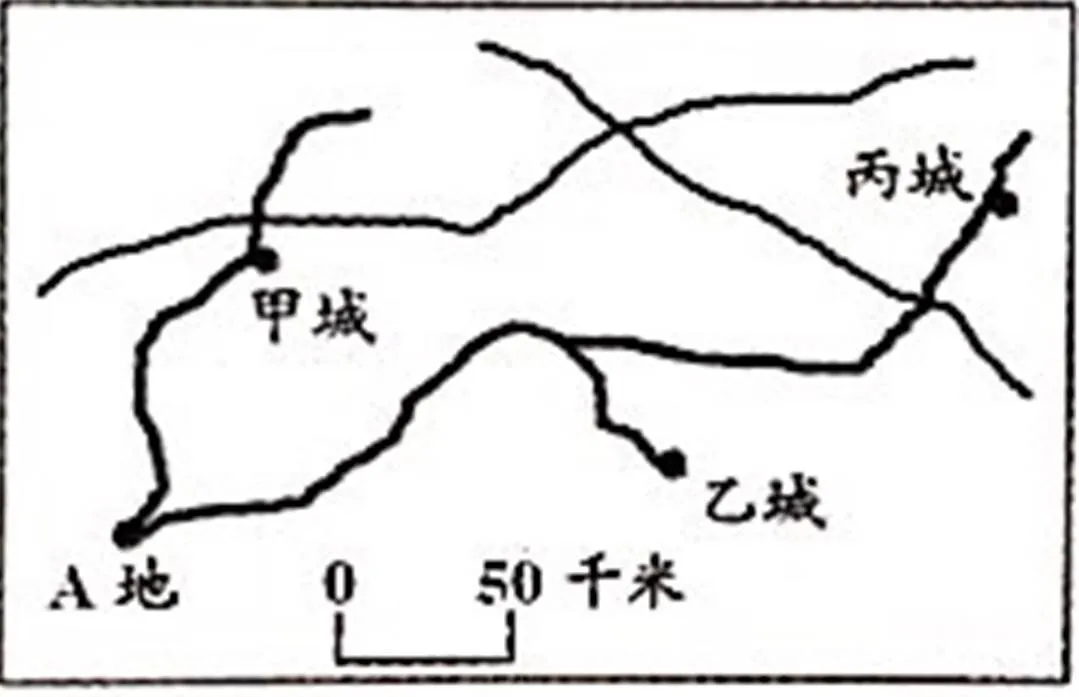
图5
如图5所示,一辆汽车早上8:00从A地出发,以平均每小时60千米的速度行驶,11:30到达目的地。目的地应该是()城。
赏析:此题需要学生应用多种知识解决:求经过时间、行程问题、应用比例尺求图上距离、化曲为直估计长度等知识。学生应先算出汽车用了3.5小时行驶了210千米,根据线段比例尺推算图上距离约是4厘米多一些,而A地到三个城市的路线又是曲的,还应有“化曲为直”的思想进行估计,目的地应该是乙城。一道题承载众多知识点,对学生的综合能力是一种考验。
好题6:

图6
图7
一个无水的长方体玻璃缸(图6),长48厘米,宽25厘米,高30厘米。有一水龙头从8:00开始向玻璃缸内注水,水的流量为每分钟8立方分米。8:03关闭水管停止注水。8:04在玻璃缸内放入一个高为16厘米的长方体铁块,全部浸没于水中。玻璃缸的水面高度(单位“厘米”)从注水到放入铁块的变化情况如图7。
(1)图7中点()的位置表示停止注水。(从点A、B、C中选择)
(2)8:03时玻璃缸水面高度为()厘米。
(3)请列式计算,求出长方体铁块的底面积。
赏析:此题主要是等积变形思想的题型,需要学生具有“转化”的思想,其中还需要学生具备读图能力、运算能力、简算意识等,可谓综合性强大。第(1)题哪个点表示停止注水,学生通过图7进行分析,A、C两点的时间点与停止注水不符,也可以从线的变化趋势进行分析,A-B呈直线上升,时间和水面高度成正比例,说明水龙头是开着的。B-C水的变化与前面不同,点C是放入铁块,水面会比点B时上升,因此点B表示停止注水。第(2)题求8:03时水面高度,可以通过“注入水的总体积÷底面积”的方法解决,这里还涉及单位转换的问题,在计算底面积“48×25”时还能考查学生的简算意识,能否主动将48进行拆数。第(3)题等积变形,将放入长方体铁块体积转化为上升部分水的体积,在计算“48×25×(24-20)”时,考查学生能否灵活运用乘法结合律进行运算。一道题蕴含着多方面知识,不愧为考查学生综合能力的好题。
评价关注点的转变必定带来命题落脚点的转变,习题、试题的编制应基于学生、基于生活、基于课程、基于发展。除了检查基础知识、基本技能的掌握情况,还应着眼学生的知识获取过程,考查活动经验的积累情况,以及思维水平的发展状况,多搜集好题、学习好题、编制好题,切实提高学生的知识技能,发展思维,提高核心素养。
G622
A
1002-7661(2022)01-0180-03

