在线测试对提高统计图表认知与理解能力的调查分析

孙红卫 王 玖 韩春蕾 刘海霞 张中文 张 俊 李开心

1 滨州医学院卫生统计学教研室，264003 山东 烟台；2 滨州医学院烟台附属医院，264003 山东 烟台

各级卫生部门和机构发表越来越多包含统计图表的报告，如从统计角度描述人群的健康状况[1]，统计图表提供了一种可视化的方法来总结影响健康状况的变量之间的关系。统计图表通过适当的方式分析并组织数据，让复杂难懂的数据易于理解，能实现信息的有效传递[2]。为了能及时有效地传达信息，统计图表需要及时更新、减少认知偏差和降低理解成本[2]。另外，能够阅读和解释在新闻媒体或一般业务中遇到的统计图表，才能熟练运用其包含的信息来进行相关问题的决策。

Schield M[3-4]认为，阅读比率和百分比的表格和图表，并且对数据进行准确描述和比较是困难的。2002年由W.M.Keck统计素养项目举办的关于阅读百分率有关的统计图表的调查，调查对象包含了美国和南非的大学生、大学教师和有经验的数据分析师，研究发现44%的大学生对单个百分比的描述有误；在饼图的比较中，有53%的数据分析师错误理解了2个部分的比较；在阅读X-Y图中，有81%的大学教师对高多少倍的比较理解有误；研究者认为统计教育者需要承担起对率和构成比等汇总数据正确描述和比较的责任[5-6]。在国内，孙恺[7]也对统计图表进行了深入系统的分析研究，梳理了统计图表的历史发展状况，阐明了统计图表的含义和组织构成，重点探讨了“时间序列统计图表”“空间序列统计图表”“时空序列统计图表”和“数量关系统计图表”4种主要视觉形式。蒋志华等[8]调查了中国12个省的2 800名一般公众对于收集和整理数据方法的掌握、统计调查能力、常用统计软件操作能力和解释统计结果能力的掌握情况。

图形设计与人们理解图形的能力之间的关系在认知心理学、教育、人机工程学和统计学等领域得到了广泛的研究。在国内还没有做过大学生对于阅读率和百分比的统计图表的理解和掌握能力的研究。这方面知识虽然从数学原理上不如统计推断或多元统计复杂，但是广泛应用于各级卫生部门和机构以及新闻媒体发布的报告中。公众对于这方面知识的理解和掌握并不到位。在统计学的教学过程中，统计图表占的学时较少，在有限的学时内提高学生的统计图表理解能力也是一个挑战。本研究在参考M.Schield[5-6]阅读比率和百分比的统计图表的调查问卷基础上，结合学习过程中易出错的知识点，设定2次测试，每次测试都列出答案解析，旨在考察在线测试工具在提高学生统计图表认知方面的作用。

1 资料与方法

1.1 研究对象

研究选择山东省某医学院校在读大学生作为调查对象，其中临床医学、麻醉学、影像学、检验学等医学专业的学生，已学完《医学统计学》(32学时)的统计图表内容；统计学专业学生，已学完《卫生统计学》(96学时)的统计图表内容。

1.2 研究方法

通过线上问卷的方法收集相关信息。线上问卷包括统计图表调查测试一(https://ks.wjx.top/jq/92107364.aspx)和统计图表调查测试二(https://ks.wjx.top/jq/92106453.aspx)2次测试；其中测试一包括基本情况、统计图表测试题目和难易度评价3个模块；测试二包括基本情况、统计图表测试题目和自我评价3个模块。2个测试中最核心模块为统计图表测试题目，包含饼图(1个分组因素的构成比)、条形图(2个分组因素的构成比)、散点图(2个变量相关关系)、表格数据信息(率的理解、死亡率和病死率的理解)的读取这5个考察类型题目。在题目选择上，2个测试对应的每个题目考察的知识点相同，但案例不同。

通过2个测试，主要考察“在线测试”+“查看答案解析”的方式是否有助于提高学生对统计图表的理解能力，所以要求被调查学生在测试一答题结束后查看问卷后设置的所有题目的解析，再进行测试二的测试。

1.3 统计学方法

研究通过SPSS 22.0软件完成分析。定性资料的统计描述采用频数和率/构成比(%)，定量资料的描述采用均数。定量资料的比较采用配对t检验或秩和检验。检验水准α=0.05。

2 结果

2.1 一般特征

本次调查共回收问卷1 100份，通过对所回收部分存在问题的问卷进行整理与剔除，最终有效问卷共957份，有效率为87.00%；957份有效问卷中，完成测试一的人数为546，完成测试二的人数为476。见表1。

表1 研究对象基本资料

2.2 对1个分组因素构成比的理解认知情况

以测试二为例(题目详见测试一和二中B1.1～B1.2题)：请根据图1中的信息，判断第B1.1～B1.2题中的陈述是否正确。

B1.1题，90%的中暑战士是北方籍。

B1.2题，北方籍战士中暑的比例远远高于南方籍战士。

此题主要考察学生对饼图中构成比的理解是否正确。题目中B1.1题是构成比的正确解释，即部分占整体的比例，而B1.2题是对构成比的错误解释，即将构成比解释成率。见图1。

图1 某部队出现中暑战士的籍贯分布

通过答题正确率来看，第B1.2题回答的正确率要低于第B1.1题的正确率(测试一正确率分别为79.1%和46.9%，测试二正确率分别为94.1%和70.8%)。如测试二的B1.2题，认为“北方籍战士中暑的比例远远高于南方籍战士”说法正确，正确率只有70.8%，说明近30%的学生对于构成比错误解释成率的说法并没有察觉，从而得出明显错误的结论。见表2。

表2 对1个分组因素构成比的认知情况

2.3 对2个分组因素构成比的理解认知情况

以测试二为例(题目详见测试一和二B2.1～B2.2题)：请根据图2中的信息，判断第B2.1～B2.2题中的陈述是否正确。

B2.1题，70～80岁男性有此疾病的占20%。

B2.2题，60～70岁男性中有此疾病比例要超过其他年龄段男性。

该题亦是主要测试对于构成比的理解，但与B2.1题和B2.2题饼图的构成比题目相比，此类问题要复杂，其有2个分组因素，用直条图来展现。该问题的2个小题都是对构成比的错误解释，也就是把构成比解释成率。见图2。

图2 某疾病的年龄及性别分布

如测试二的B2.1题，20%应该是某疾病患者中70～80岁男性占的比例。测试二的第B2.2题的叙述如果改成“某疾病患者中60～70岁男性的占比要高于其他年龄段男性”就正确了。测试一的B2.2小题正确率只有33.5%，测试二的B2.2题正确率也只有56.3%。说明超过40%的学生对于“将构成比的比较解释成率的比较”的错误并没有清晰判断。见表3。

表3 对2个分组因素构成比的认知情况

2.4 对散点图及2个变量相关关系的理解认知情况

以测试二为例(题目详见测试一和二B3.1～B3.3)：请根据图3中的信息，判断第B3.1～B3.3题中的陈述是否正确。

B3.1题，随着房价变化比例的增加，妇女生育率变化比例有下降的趋势。

B3.2题，高房价会导致妇女生育率下降。

B3.3题，如果某县的房价保持稳定，则该县的生育率也会保持稳定。

该题考察学生对散点图的理解。其中B3.1题，是对散点图的正确理解。B3.2题将散点图的相关性错误解释成因果关系，B3.3题也是将散点图的相关性错误解释成因果关系，而且认为控制了“原因”，就能有对应的“结果”。见图3。

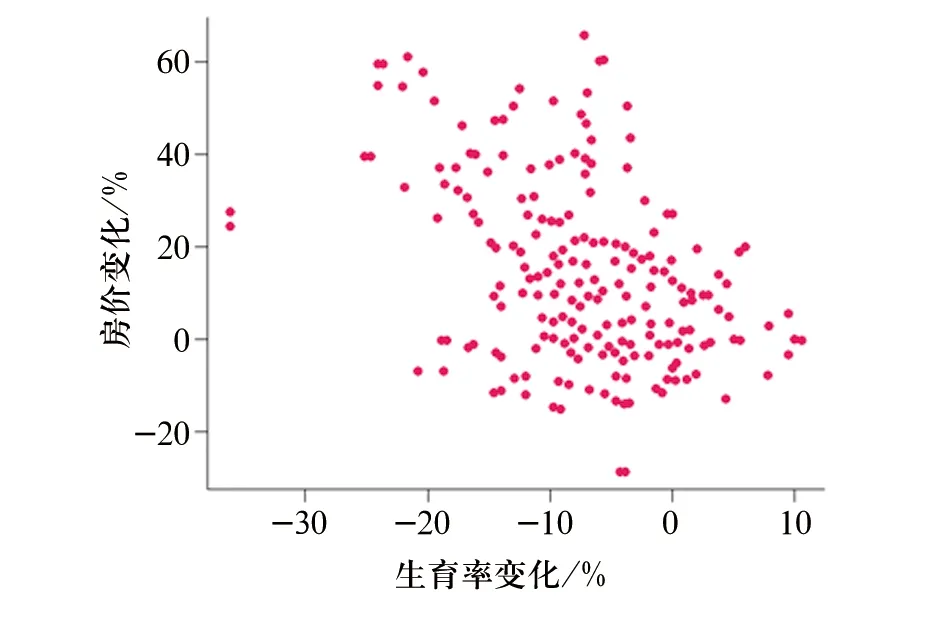
图3 2010—2016年某国多个县房价变化比例与25～29岁妇女生育率变化比例散点图

从正确率来讲，学生的正确率较高，基本都在70%以上，说明学生对于散点图的理解整体把握较好。但仍有30%左右的学生会将散点图的相关性错误解释成因果关系。见表4。

表4 对散点图及相关关系的认知情况

2.5 对率的理解认知情况

以测试一为例(题目详见附录中测试一和二B4.1～B4.2)：表5表示了美国及其各州在1990、1995和1996年的低出生体质量儿的比例。

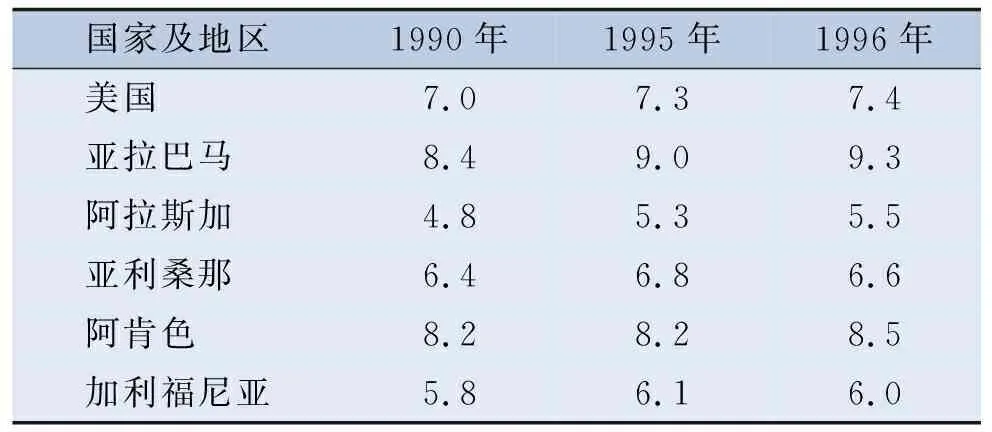
表5 美国及其各州1990、1995和1996年 低出生体质量儿比例 单位：%

据表5中比例回答B4.1～B4.2中的问题。

B4.1题，在1996年的美国，6.0%的低体质量婴儿出生在加利福尼亚。你认为此叙述准确?

B4.2题，在1996年的美国，亚拉巴马州出生的低体质量婴儿比加利福尼亚州出生的婴儿多。你认为这一说法准确地将加州的6.0%与亚拉巴马的9.3%进行了比较吗?

该问题主要考查学生对于率的理解。测试一的B4.1题，测试二的B4.1题和B4.2题，都是将率错误解释成了构成比。测试一的B4.2题是将率错误解释成了频数，也就是将相对数错误解释成了绝对数。测试一的B4.1题的正确说法应该是，6.0%表示1996年加利福尼亚州低出生体质量儿的比例是6.0%。B4.2题的正确说法应该是，1996年亚拉巴马州低出生体质量婴儿的比例要高于加州。测试二的B4.1和B4.2题的正确说法是，26.2%表示 1990年黑人男性中吸烟的比例是26.2%。测试二的B4.2题正确率只有46.0%，这说明有超过一半的学生，对于率错误解释成构成比的说法并不能清晰判断。见表6。

表6 对比例频率表中率的认知情况

2.6 对死亡率和病死率指标的理解认知情况

以测试一为例(题目详见附录中测试一和二B5.1～B5.2题)：表7给出了新型冠状病毒肺炎疫情各地区患者治愈率与病死率。

根据表7回答下面B5.1～B5.2题。

B5.1题，至截止日期在地区C每100个人中平均有6.22人因新型冠状病毒肺炎而死亡。

B5.2题，至截止日期地区C的死亡人口中因新型冠状病毒肺炎死亡的人数占比为6.22%。

该问题主要考查学生对于死亡率和病死率的理解。其中测试一的B5.1题是将病死率错误解释成死亡率。B5.2题是将病死率错误解释成死亡构成比。可以看到这2个小题的正确率在70%左右。测试二的B5.1题和B5.2题是对死亡率的正确解释。这两2个小题的正确率分别是46.0%和63.9%。说明有30%～50%的学生对于死亡率、病死率以及死亡构成比的区别没有掌握。见表8。

表8 对死亡率和病死率指标的认知情况

在2个测试的11个题目中，全做对的都只有5%左右，判断错误的题目≤3个的学生占有55%左右，也就是说有45%左右的学生在测试中会在11个题目中错4个或以上。25%的学生在11个题目中错5个或更多。测试一和测试二的平均分相差不大，且对其进行配对样本的t检验，差异无统计学意义(t=0.348，P=0.728)。见表9。

表9 2次测试得分对比结果

①数据为平均值。

经过学习后，有69.1%的学生主观上认为自己有所提高，29.0%的学生主观上认为自己做题时没有变化，极少数的学生认为自己有所下降。通过对医学院大学生统计图表的认知理解情况的调查发现，相当一部分学生对于基本统计图表的理解错误。其中对于2个分组因素构成比理解有误的，达到70%，对于1个分组因素的构成比理解有误的，达到50%左右，对于率的理解30%～50%的学生理解错误，30%左右的学生对病死率和死亡率的区别不能清晰判断，30%左右的学生对散点图的相关关系理解有误。测试二相比于测试一，将近70%的学生自我评价通过测试后对统计图表的理解有提高。见表10。

表10 经过学习后学生自我认为的掌握程度认知情况表

3 讨论

在线测试再结合答案解析以及老师重点讲解，结果可能会更好。2002年，W.M.Keck统计素养项目进行了一项关于阅读率和百分比图表的国际调查。调查的重点是表格和图表中的比率和百分比，调查发现了较高的错误率。而帮助学生学习这些技能需要相当长的时间，由T.Burnham和M.Schield[9]开发的新在线工具可以解决这些问题，这个工具是基于web的程序来帮助学生准确描述比较率和百分比，并用不同的表格呈现，并且对学生的错误给予即时反馈。使用这个在线程序后，上课时间至少减少了50%。该工具使在线教授统计知识成为可能[10]。

本研究采用的2次测试也是通过在线测试的方式来帮助学生掌握这部分的内容，通过结果可以看到，学生自我评价这种方式对于学生是有帮助的。但2次测试的平均分差异无统计学意义，本研究并没有要求在线测试的成绩计入课程的平时成绩，所以对学生缺少激励，可能有的同学急于完成问卷，测试二的答题速度较快；也可能有同学并没有仔细阅读答案解析，做测试二时还是出现错误。另外，2次测试虽然采用的知识点相同，但采用的案例不同，学生对案例背景的熟悉程度也会影响答题的正确率。这也说明，对于统计图表的正确解读离不开对相关案例背景的熟悉和理解，切不可仅凭直觉，需要在对案例背景认真阅读基础上来理解统计图和统计指标。

本研究是对医学院大学生对于统计指标和统计图表的认知理解情况进行调查，相当大部分以后会进入临床、基础研究还有公共卫生领域工作，都需要理解并掌握统计指标和统计图表，并通过其所提供的信息进行决策。所以在涉及在线测试题目时，如果能够结合医学应用，如针对临床专业的学生，设计反映治疗方式优劣的统计图表；针对统计学和预防医学专业，设计反映疫情或其他疾病发展的统计图表，会促进学生掌握将来工作中常用的统计图表，使得他们能更好地结合数据信息作出判断和决策。

统计图表是传达信息的有效手段，虽然从统计知识的难度上相对比较简单，但是统计图表的可读性和公众的理解能力亟待改进。设计者需要增加统计图表的可读性，大学生、从业者、公众也需要增加对统计图表的理解能力。统计图表的理解和掌握仅通过课堂讲解的方式，由于学时的限制无法达到准确理解的目标。通过在线测试的方式，根据案例设计题目，再结合答案解析，可以在有限的学时内将这部分知识掌握得更好。