血压调控KCa2.3离子通道对瓣膜性房颤影响的分子动力学模拟

刘 岩,孙 毅,张桂敏,夏健明,张洪明*

(1.昆明理工大学 力学系，云南 昆明 650500；2.云南阜外心血管病医院，云南 昆明 650032)

KCa2.3离子通道蛋白是分布在人体心肌细胞隶属于小电导钙离子激活的钾离子通道(small-conductance Ca2+-activated K+channel，SK Channel)，对钾离子有高度选择性[1]。当细胞质内游离的钙离子浓度上升后会被激活，从而开放钾离子通道，产生钾离子外流，钾离子外流是通过各类钾离子通道实现的，钾离子通道是生物体内分布最广泛、最复杂的一类离子通道[2]，SK离子通道就是钾离子通道中的一类。钾离子外流产生的动作电位会引起超极化后电位(afterhyperpolarization potential， AHP)现象， 超极化后电位对动作电位反复激动现象有抑制作用，以保证细胞的各项生命活动[3]。但是KCa2.3离子通道开放程度过大会使心房肌的动作电位时长明显缩短[4]，从而会引发一些心血管疾病。

近几年的研究表明，通过减小钾离子外流可以有效减少某些心血管疾病尤其是房颤(valvular atrial fibrillation，VAF)的病发率[5]。我国的孙曼青[6]、苑磊[7]、LI[8]等的研究里表述了SK离子通道在人的心肌细胞里广泛分布，且当血压发生变化时，SK离子通道内的电流也有较明显波动。XU等在2003年发现SK通道分布心房优于心室[9]。TAKAI等在2013年发现KCa2.3离子通道受心脏内湍流切应力调控[10]。因此，对KCa2.3离子通道蛋白表达的进一步深入研究有科学应用价值。

本文基于超级计算机和分子动力学模拟软件Gromacs，模拟计算了KCa2.3离子通道蛋白在不同压力下对钾离子外流的调控程度，分析了不同血压下钾离子外流的速度。

1 计算模型及研究方法

1.1 模拟原理

分子在整个环境中所受力场分为动能和势能，势能包括非键结势能(Unb)、键的伸缩项(Ub)、键角弯曲项(Uθ)、二面角扭曲项(Uφ)、离平面振动项(Uχ)、库伦作用项(Uel)，总势能公式如下：

U=Unb+Ub+Uθ+Uφ+Uχ+Uel

(1)

依照经典力学，系统中任一原子在环境中所受的力为:

(2)

式中，r为体系中原子的位置，通过数值求解牛顿方程模拟原子的运动。

(3)

最后得出每个原子的速度、位置信息。

1.2 KCa2.3通道工作机理

KCa2.3离子通道是小电导钙激活钾离子通道的一种，由KCNN3编码，α亚单位和β单位组成，如图1所示：

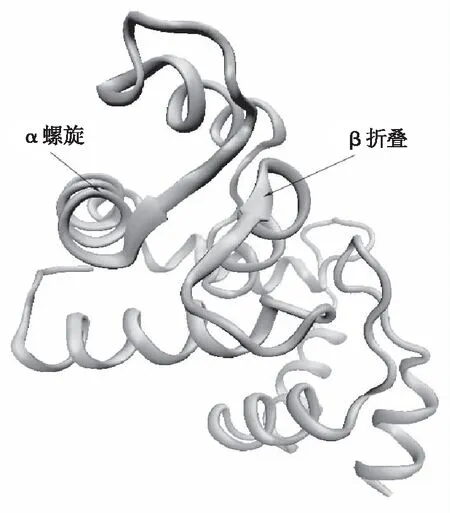
注：螺旋形表示的是α亚单位，固形箭头表示的是β单位。

KCa2.3离子通道蛋白有1个单通电导，并受细胞内Ca2+调控。KCa2.3离子通道作用机理如下：

a)当细胞质内钙离子处于高浓度状态时，钙离子及钙调蛋白(CaM)会结合KCa2.3离子通道的α亚单位，见图2(a)；

b)KCa2.3离子通道缓慢激活、开放，见图2(b)；

c)细胞质内钾离子外流，见图2(c)；从而产生动作电位。

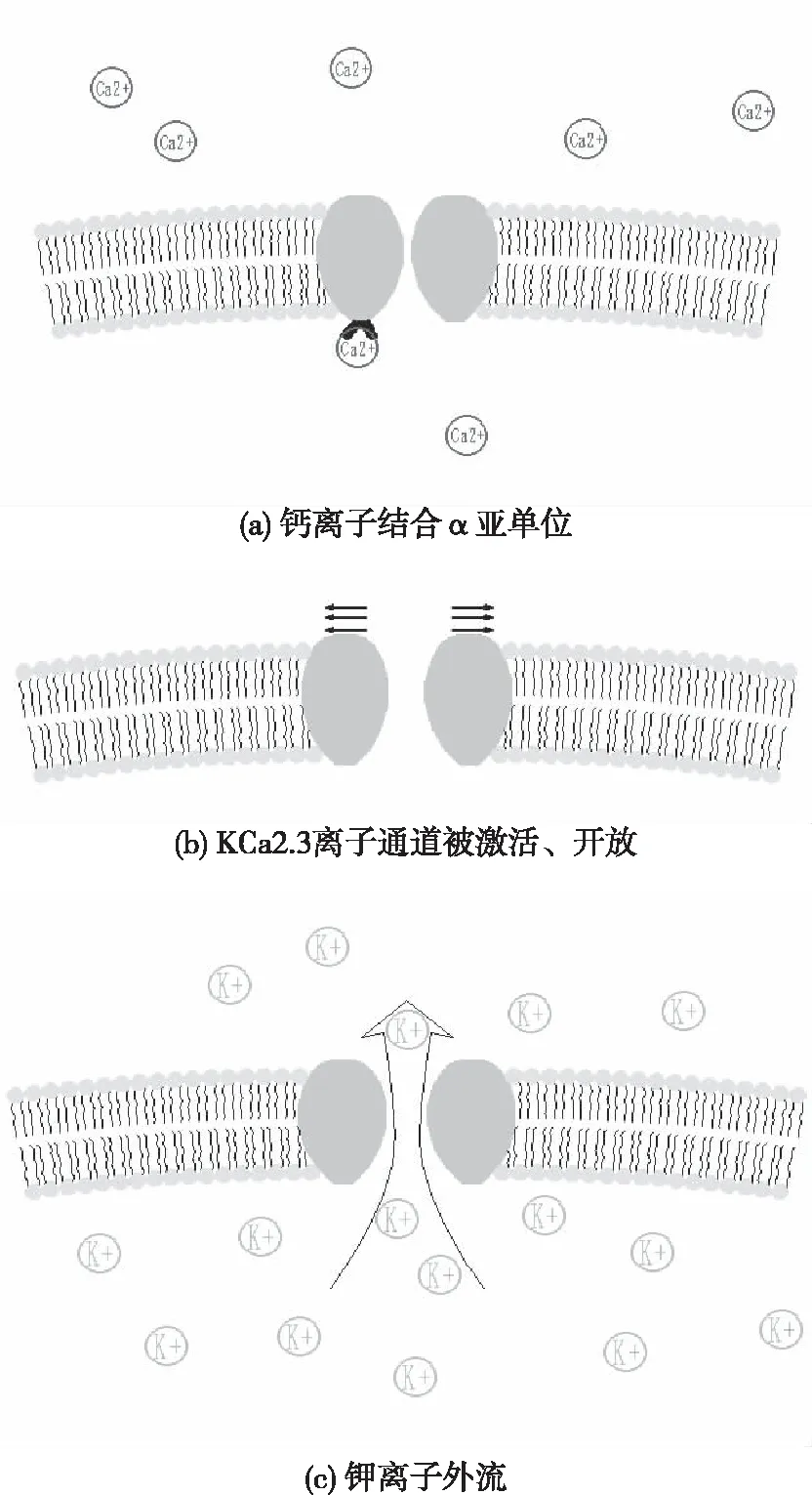
图2 KCa2.3离子通道激活过程

1.3 软件及控制变量的数值选取

本文采用Gromacs软件进行模拟，力场选取全原子(OPLS-AA/L all-atom)力场[11]，水分子模型采用SPC/E模型。体系压力通过Parrinello-Rahman[12]控制，其数值分别设置为60、70、80、90、100、110、120、130、140、150、160、170、180 mmHg；温度耦合由Nose-Hoover[13]控制，数值设置为310 K；静电相互作用采用Particle-Mesh-Ewald算法进行处理；范德华力计算采用截断Cut-off方式，计算截断值设为0.12 nm。

1.4 构建分子模型

构建分子模型步骤如下：

a)在蛋白质数据库下载并修改KCa2.3离子通道的分子模型，修改后的模型如图3所示。左图为蛋白质的全原子模型，右图为蛋白质泛素的模型。

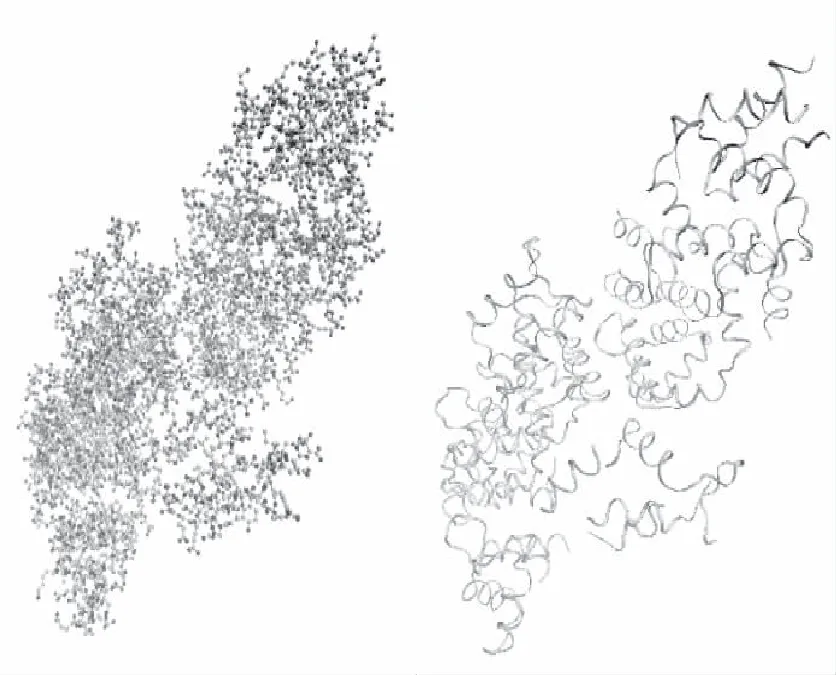
(a)全原子模型 (b)泛系模型

b)利用分子建模软件构建钙离子和钾离子模型；正常生理状态下，细胞内、外钙离子和钾离子的浓度如表1所示。

表1 钙离子和钾离子浓度表

结合该数据，将一定数量的钙离子、钾离子分别固定在KCa2.3离子通道蛋白的两侧，整个模拟体系在6 nm×6 nm×52 nm的盒子中进行，如图4所示。

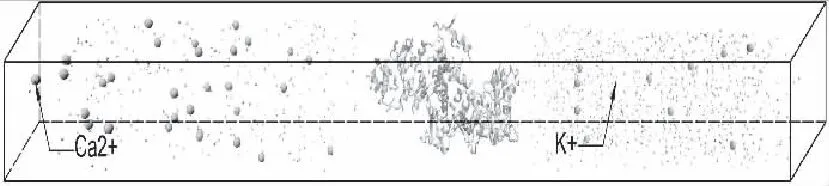
图4 分子动力学模拟体系

图中大的离子表示钙离子，小的离子表示钾离子，体系中间为KCa2.3离子通道蛋白。

c)加入正/负离子(Na+/Cl-)以保证体系的电荷守恒。表2是加入Cl-之后，分子动力学模拟体系内各单位的数量。

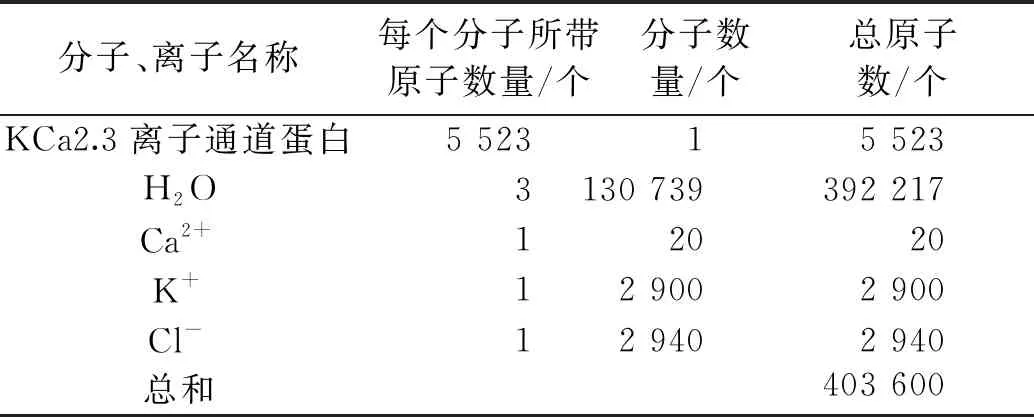
表2 各单位原子数量

d)进行能量最小化模拟，优化初始模型。初步进行能量最小化模拟，采用最速下降法，将最大能量设置在1 000 kJ/mol，防止分子模型在初始阶段受分子间势能影响进行其他运动。

1.5 参数设置

本次模拟仅研究不同压力下KCa2.3离子通道对钾离子的调控作用，设置温度耦合为恒温环境，温度场为36.85 ℃(310 K)，步数为1×105，步长为1fs(1fs=1×10-15s)，耦合总时长为0.1 ns。

压力耦合设置选用60～180 mmHg共 13组压力值，每组数据步数均为1×105，步长为1fs，耦合总时长为0.1 ns。

进行最终分子动力学模拟时，步数选用1.5×106步，步长为1fs，总时间为1.5 ns，每50 ps保存一次轨迹文件。

2 计算结果

2.1 扩散系数

通过观察钾离子的扩散系数，我们可以直观的看到钾离子通过KCa2.3离子通道蛋白流出细胞外的程度，扩散系数越大，钾离子外流速率越快。而Gromacs软件中并不能直接给出钾离子的扩散系数。因此，我们需要根据其均方位移(mean-square displacement，MSD)函数计算出钾离子在不同压力体系下的扩散系数。

均方位移表示的是某一原子相对起始位置的位移量，其公式为：

MSD=〈|r(t)-r(0)|2〉

(4)

再结合爱因斯坦的扩散定律得到，

limt→∞〈|r(t)-r(0)|2〉=6Dt

(5)

计算得出钾离子的扩散系数为，

(6)

式中,D为粒子扩散系数(diffusion constant)且为常数，所以模拟时间t与钾离子的均方位移为一次函数关系。图5为同一体系在不同压力下钾离子的MSD函数，其斜率为钾离子的扩散系数。

图5 体系在不同压力下的MSD函数

从表中我们可以看出在压力在90 mmHg时，MSD函数斜率最大；压力在140 mmHg时，MSD函数斜率最小。因此,当血压为90 mmHg时，钾离子外流速率最大，血压为140 mmHg时，钾离子外流速率最低。根据图5的MSD函数曲线，可以得到不同压力对应钾离子扩散系数，如表3所示。

表3 不同压力对应的钾离子扩散系数

根据表3绘制压力和钾离子扩散系数的样条曲线如图6。从图中可以看出压力与钾离子扩散系数的关系呈“U”型，当压力在120～150 mmHg之间时，钾离子扩散系数最低，而当压力小于120 mmHg或者大于150 mmHg时，钾离子扩散系数变大，钾离子外流程度增大，较120～150 mmHg时增大了3.19%～6.12%。该数据与邢爱君统计研究[14]发现的当收缩压处于120～140 mmHg时发生心血管疾病死亡风险最低的结果范围大致一致。

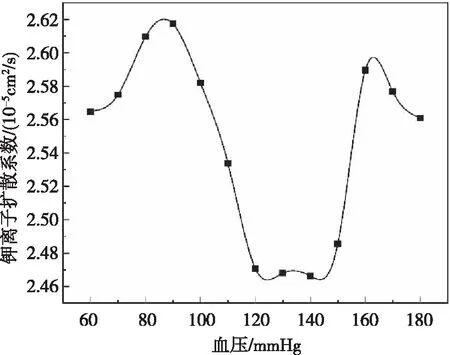
图6 压力与钾离子扩散系数的关系

2.2 体系的自由能分析

自由能是影响系统变化的重要因素，其中分子非键作用势能占绝对主导地位，其主要包括分子间的范德华力和分子间的静电力两部分。

(7)

式中，εij是第i个原子和第j个原子之间相互作用势能的最小值；σij是第i个原子和第j个原子之间达到平衡的距离；rij是第i个原子和第j个原子之间的绝对距离；qi，qj是该原子的电荷量；ε0是介电常数，ε0=1/4πk。

图7是模拟体系在进行压力耦合前做的能量最小化数据，在模拟达到6 325步后，系统趋于平衡，其能量最小值(Epot)为-7.215×106kJ/mol。此时，体系达到最稳定的状态，与模拟过程中体系内相互作用能进行对比(图8)，在模拟过程中能量最大为-7 140 348.5 kJ/mol，能量最小为-7 224 514.5 kJ/mol，波动范围在84 116 kJ/mol之间。因此，随时间变化体系内的自由能稳定性能未发生改变，说明在KCa2.3离子通道工作时未发生化学反应，且各原子动能未发生较大变化，各原子的运动速度是一个定值。

图7 能量最小化过程中势能的变化

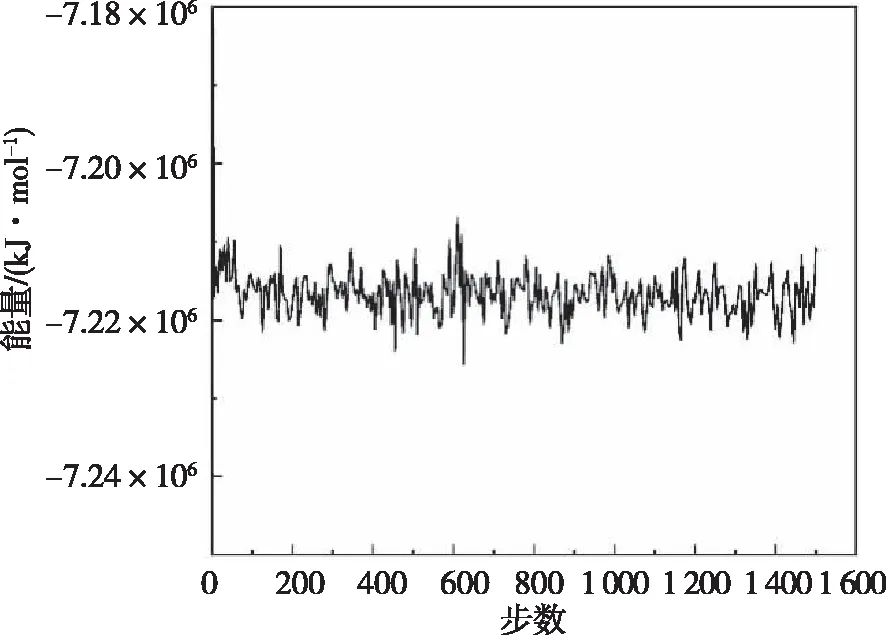
图8 钾离子与KCa2.3离子通道蛋白之间的相互作用能

2.3 KCa2.3离子通道在不同压力下的稳定性

均方根偏差(root mean square deviation，RMSD)是衡量模拟过程中蛋白质稳定性的重要指标，当模拟后的蛋白质位置与初始状态的位置偏差较大时，RMSD值就会越大，其计算公式为：

(8)

式中,rij表示j时刻对应i原子的坐标位置;ri0表示初始时刻原子所在的位置。

图9、图10分别为体系在压力为60 mmHg和180 mmHg时的RMSD变化趋势。从图中我们可以看出，随着模拟时间的增加，蛋白质与其初始位置的距离也变大，且均在模拟0.8 ns后，其结构趋于稳定，其位移大致为0.45 nm和0.49 nm。体系在其他压力状态下KCa2.3离子通道蛋白的位移均在0.45～0.49 nm范围内，对比心肌细胞直径的15 μm可以忽略不计，说明压力对KCa2.3离子通道蛋白的稳定性没有影响或是影响较小。

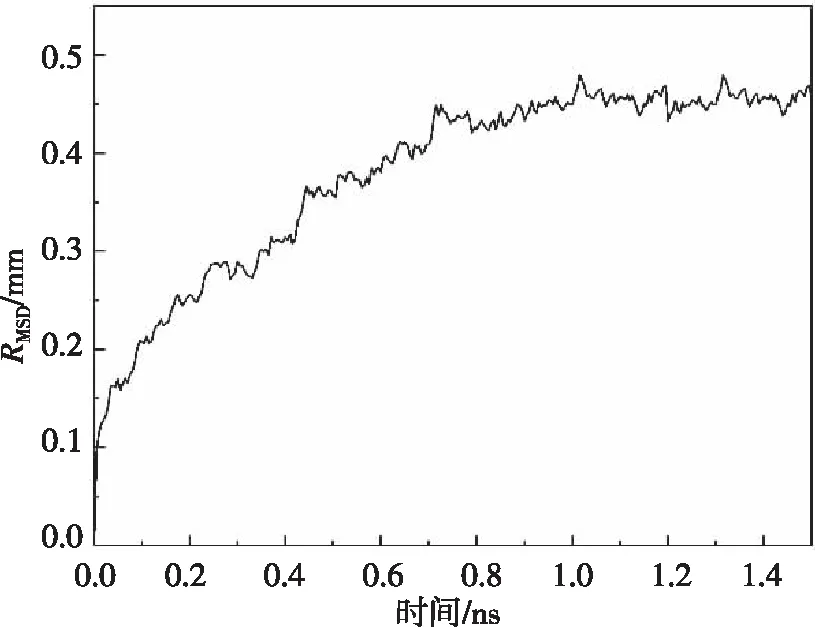
图9 60 mmHg时分子模拟过程中的RMSD值

图10 180 mmHg时分子模拟过程中的RMSD值

为了更直观地观察不同压力下KCa2.3离子通道蛋白的变化情况，我们将模拟前后的KCa2.3离子通道蛋白构型放到同一体系内进行观察对比，如图11所示。

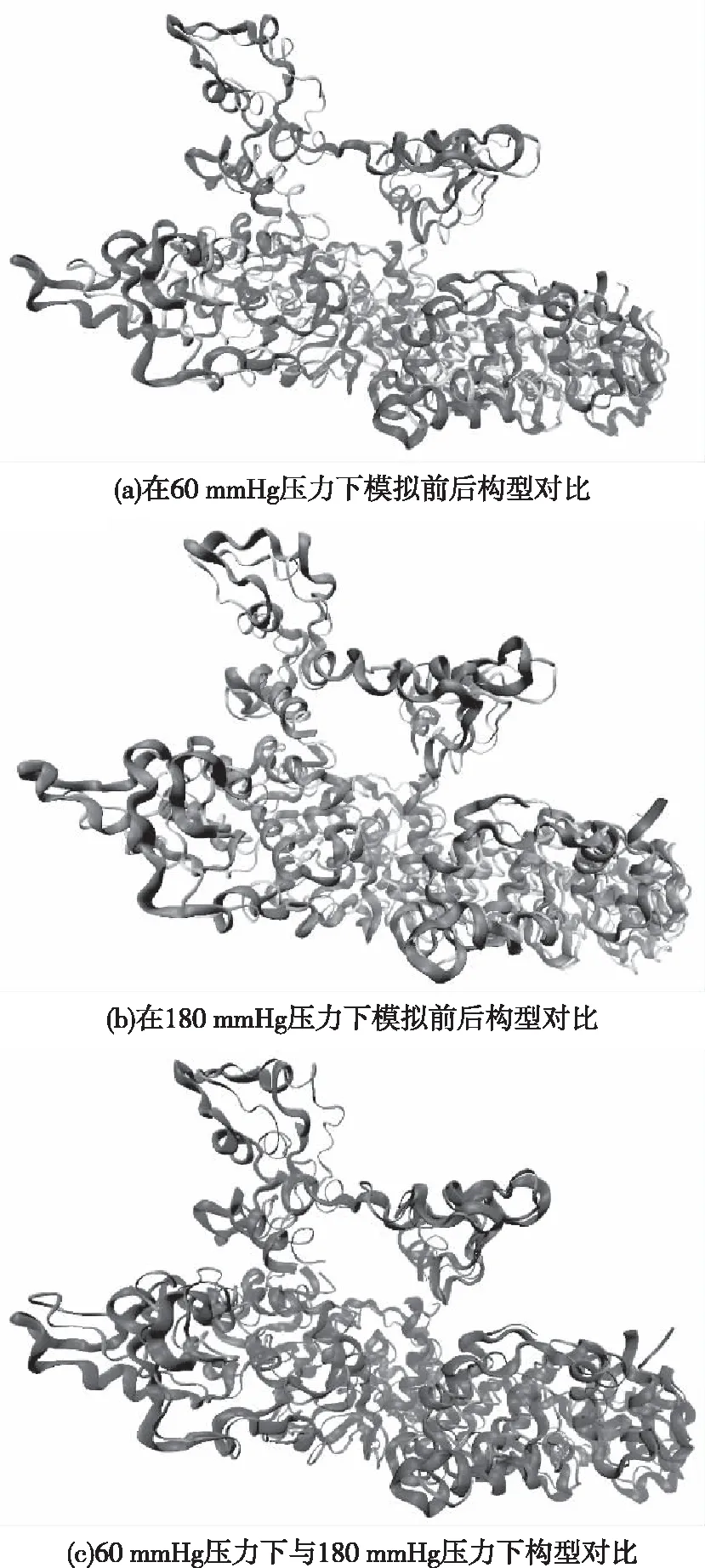
图11 模拟前后KCa2.3离子通道蛋白构型对比

图11(a)、11(b)中较薄的构型为体系模拟前的分子构型，图11(c)中较薄的构型为体系在60 mmHg压力下的分子构型。通过对比发现KCa2.3离子通道蛋白在模拟前后，结构上有细微差异；而60 mmHg压力下与180 mmHg压力下KCa2.3离子通道蛋白结构没有发生变化，仅在模拟后的位置上有细微差异，进一步验证了压力对KCa2.3离子通道蛋白的稳定性没有影响。

2.4 分子聚集特性

径向分布函数(radial distribution function，RDF)其物理意义如下：

设中心距离为r到r+dr圆环内的原子数目为dN，RDF函数g(r)为

ρg(r)4πr2=dN

(9)

解得,

(10)

当RDF值越接近1时，表示该区域范围内的密度越接近平均密度。我们可以根据径向分布函数查看钾离子之间最短距离，对比不同体系中钾离子之间的径向分布函数，发现其分布函数没有较大差异。图12是在100 mmHg压力下体系以钾离子为中心，距离中心r到dr的圆环内钾离子数目的径向分布函数。

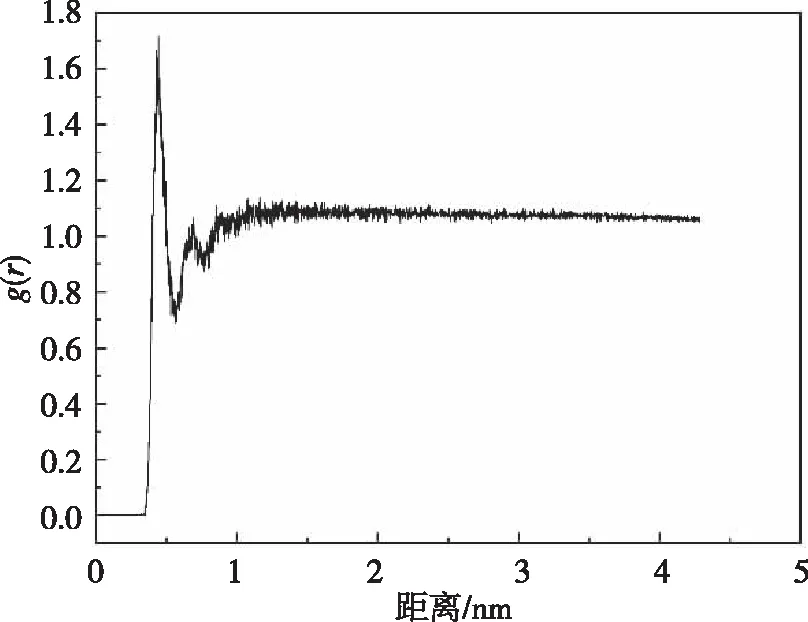
图12 系统在分子模拟过程中的RDF函数

在0.338 nm处RDF函数值开始不为零，即在该系统下两个钾离子之间最短距离为0.338 nm，当距离为0.434 nm时，径向分布函数值达到最大值为1.631。在其他压力情况下，当中心距离越大时，RDF也都是趋近于1。说明钾离子在外流的过程未出现聚集现象，钾离子在整个模拟过程中都是均匀分布在细胞液内。

3 结论

为了研究KCa2.3离子通道蛋白在不同压力环境下各方面性能的差异，本文采用分子动力学模拟的方法，对同一体系在13种不同压力下进行了分子动力学模拟。通过分析和对比KCa2.3离子通道蛋白在表达时不同压力状态下钾离子的扩散系数、体系内的势能与KCa2.3离子通道蛋白的RMSD函数、体系能内势能的变化、钾离子的径向分布函数，得出以下结论：

1)KCa2.3离子通道蛋白受压力影响，二者之间的关系呈“U”型，当压力处于120～150 mmHg时，通过KCa2.3离子通道蛋白的钾离子数量较其他压力状态下少3.19%～6.12%；

2)KCa2.3离子通道蛋白在表达时未发生化学反应，仅为各原子之间势能的转移；

3)压力对KCa2.3离子通道的稳定性没有影响或是影响较小；

4)KCa2.3离子通道蛋白在表达时，钾离子未出现聚集现象，其在整个模拟过程中都是均匀分布在细胞液内。