团簇Co3NiB2极化率、偶极矩及态密度研究
方志刚,王智瑶,郑新喜,秦 渝,毛智龙,曾鑫渔,朱依文,王 倩
(辽宁科技大学 化学工程学院,辽宁 鞍山 114051)
物质根据其内在的原子排列方式可以划分为两种,即原子呈规则排列的晶体材料和原子呈无规则排列的非晶体材料。自从1934年德国物理学家Kramer等采用蒸发沉积法制备出非晶态薄膜[1],对于非晶态合金的合成与应用研究便迅速开展起来。而随着现代工业技术的飞速发展和人们环保意识的不断提高,如何得到清洁、可持续的能源载体来替代传统化石燃料,以解决一次能源的匮乏和环境污染严重等问题,已经引起了大众的密切关注。现如今,通过借助各种催化剂来电解水以获得可持续发展的清洁能源(氢气),是科学家们惯用的方法之一[2-3]。在经过大量实验验证后发现,处于热力学亚稳态的非晶态合金,因其长程无序、短程有序的“玻璃态”各向同性排列的结构特点,而具有不同于传统金属材料的优异性能[4-7]。例如,CHENG等[8]基于双金属间的协同作用发现,非晶态Co-Ni体系掺杂非金属原子的加氢催化活性明显优于单金属原子与非金属原子组合成分的活性。文献[9-11]通过研究发现,过渡金属原子掺杂非金属原子所形成的非晶态合金,因其内在的协同效应,在一定程度上提高了物质的催化性能;而非晶态合金“玻璃态”各向同性排列的特点,也使其表面分布更多的活性位,以达到吸附更多反应物分子的目的,从而增强对反应物的活化能力[12]。查阅大量文献后发现,作为催化剂领域的佼佼者,非晶态合金体系一直是科学家们研究的热点对象,其中非贵金属化合物Co-Ni-B三元体系,更是因被证实在催化方面具有优异性能而备受青睐[13-15]。鉴于非晶态Co-Ni-B三元体系具有优异的催化性质,其常被用于不同类型反应的催化剂,这也就意味着,非晶态合金Co-Ni-B三元体系具有较强的研究意义和广阔的发展前景。但截至目前,对于该体系的研究大多停留在宏观实验角度,微观理论方面的研究鲜少,因此,本文以已构建出的Co3NiB2团簇模型为基础[16],对其极化率、偶极矩及态密度方面进行微观理论的探究,以期能为今后有关非晶态合金Co-Ni-B三元体系的研究提供有价值的理论参考。
1 计算方法
基于拓扑学原理[17]并依托于HP-Z440计算机上的Gaussian09程序,在B3LYP/Lan12dz水平下,对团簇Co3NiB2所设计出的全部初始构型,采用密度泛函理论[18-20],在自旋多重度为二、四的情况下进行全参数优化和相关频率计算。对计算所得12种优化构型的过渡金属Co、Ni原子采用18-eECP双ξ基组(3s,3p,3d/2s,2p,2d),对类金属B原子采用Dunning/Huzinaga双ξ基组(9s,5p/3s,2p)[21-24],其中与态密度相关的各项参数均使用Multiwfn程序[25]完成。
2 实验结果与数据分析
2.1 团簇Co3NiB2的优化构型
依据上述计算方法,对优化所得的稳定构型进行整理和筛选之后,可将团簇Co3NiB2中的相同构型和含虚频的不稳定构型排除,最终得到如图1所示的12种优化构型,其分别以五棱锥、单帽四棱锥、单帽三角双锥、四角双锥4种空间结构类型存在。
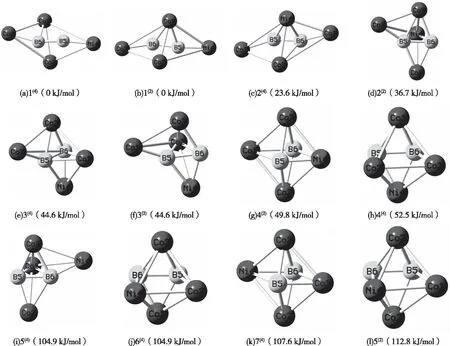
图1 团簇Co3NiB2的优化构型
为方便进一步探究,设能量最低的五棱锥构型1(4)的能量为0 kJ/mol,将其余优化构型的相对能量由低到高进行排序。其中,能量越低,稳定性越强。结合构型能量与空间结构分析可得,团簇Co3NiB212种优化构型的稳定性由高到低依次为:五棱锥构型>单帽四棱锥构型>单帽三角双锥构型>四角双锥构型。
2.2 团簇Co3NiB2的极化率分析
电子云是表征原子或分子中电子出现的概率密度。由于电子易受到外电场中磁场的作用,因此电子云形状也会随着外场作用的变化而发生改变。极化率作为衡量电子云形状改变程度的物理量,不仅在一定程度上反映了极化过程的难易程度,而且因其对团簇结构极为敏感的特性可用于分析团簇的变形程度。与此同时,极化率还可表征物质对外界电场的响应,是描述物质与光非线性作用的物理量之一,在一定程度上反映出了分子间碰撞过程中的色散力、诱导力和取向作用力等力之间的联系和作用,是分析物质变形性的常用手段。
极化率张量平均值是极化率在xx、yy和zz轴上张量的平均值。极化率张量平均值(〈α〉)越小,说明团簇结构结合得越紧密,团簇原子间的相互作用就越强,其在外场作用下就越易保持原有的电子云形状,团簇形变程度就越小;反之,极化率张量平均值越大,团簇形变程度就越大。极化率的各向异性不变量(Δα)可表征团簇在外加电场中的响应程度,是反映在外场作用下团簇极化率各向异性的物理量。Δα值越大,团簇构型就越易受到外场影响,构型极化率的各向异性就越大;反之,Δα值越小,团簇构型就越难受到外场影响,构型极化率的各向异性就越小。团簇Co3NiB2各优化构型的极化率张量平均值与极化率的各向异性不变量,通过以下公式进行计算,计算结果如表1所示。

表1 团簇Co3NiB2 12种优化构型的极化率
〈α〉=(αxx+αyy+αzz)/3

由表1数据可知:该团簇体系的极化率张量主要集中在xx(173.625~295.870 a.u.)、yy(158.509~181.113 a.u.)及zz(121.631~166.432 a.u.)3条主轴方向上,且主轴方向上的极化率张量数值远远大于xy(-10.240~10.380 a.u.)、xz(-9.087~7.585 a.u.)、yz(-3.306~4.886 a.u.)3条非主轴方向上的极化率张量。其中,极化率张量最大xx分量为构型2(4)(295.870 a.u.),最大yy分量为构型7(4)(181.113 a.u.),最大zz分量为构型5(4)(166.432 a.u.)。
分析团簇Co3NiB2各优化构型的极化率张量平均值可知:构型4(4)、7(4)的极化率张量平均值最小且相近,说明这两者的团簇结构结合得最紧密,团簇原子间的相互作用最强,其在外场作用下最易保持原有的电子云形状,团簇形变程度最小;而构型1(4)、1(2)、2(4)则与之相反,它们的极化率张量平均值最大且相近,说明这三者在外场作用下最难保持原有的电子云形状,团簇形变程度最大。由此,根据表1数据可判断,团簇Co3NiB2的形变程度由大到小依次为:1(4)>1(2)>2(4)>5(4)>3(2)>2(2)>3(4)>5(2)>4(2)>6(4)>4(4)>7(4)。结合图1各优化构型的空间结构分析可得,该团簇的形变程度由大到小依次为:五棱锥构型>单帽四棱锥构型>单帽三角双锥构型>四角双锥构型,这与2.1节中团簇Co3NiB2稳定性排序一致,说明极化率张量对团簇的几何结构具有很强的依赖性。
分析团簇Co3NiB2各优化构型的极化率各向异性不变量可知:构型4(4)、6(4)的极化率各向异性不变量最小且相近(均小于15 a.u.),说明这两者对外场的响应最弱,最不易受到外场影响;而构型2(4)、1(2)、1(4)的极化率各向异性不变量最大且均大于130 a.u.,说明这三者对外场的响应最强,最易受到外场的影响。此外,根据表1数据还可判断,团簇Co3NiB2对外场的响应程度由强到弱依次为:2(4)>1(2)>1(4)>4(2)>2(2)>3(4)>3(2)>5(4)>7(4)>5(2)>6(4)>4(4)。同样,结合图1各优化构型的空间结构分析可得,该团簇受外场影响的难易程度由强到弱依次为:单帽四棱锥构型>五棱锥构型>单帽三角双锥构型>四角双锥构型,这与2.1节中团簇Co3NiB2稳定性排序相比,仅五棱锥构型与单帽四棱锥构型的顺序进行了互换,且二者空间构型的能量值相差不大,说明极化率各向异性不变量对团簇的几何结构具有较强的依赖性,但依赖性不及极化率张量。
2.3 团簇Co3NiB2的偶极矩分析
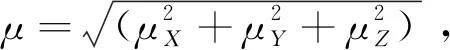
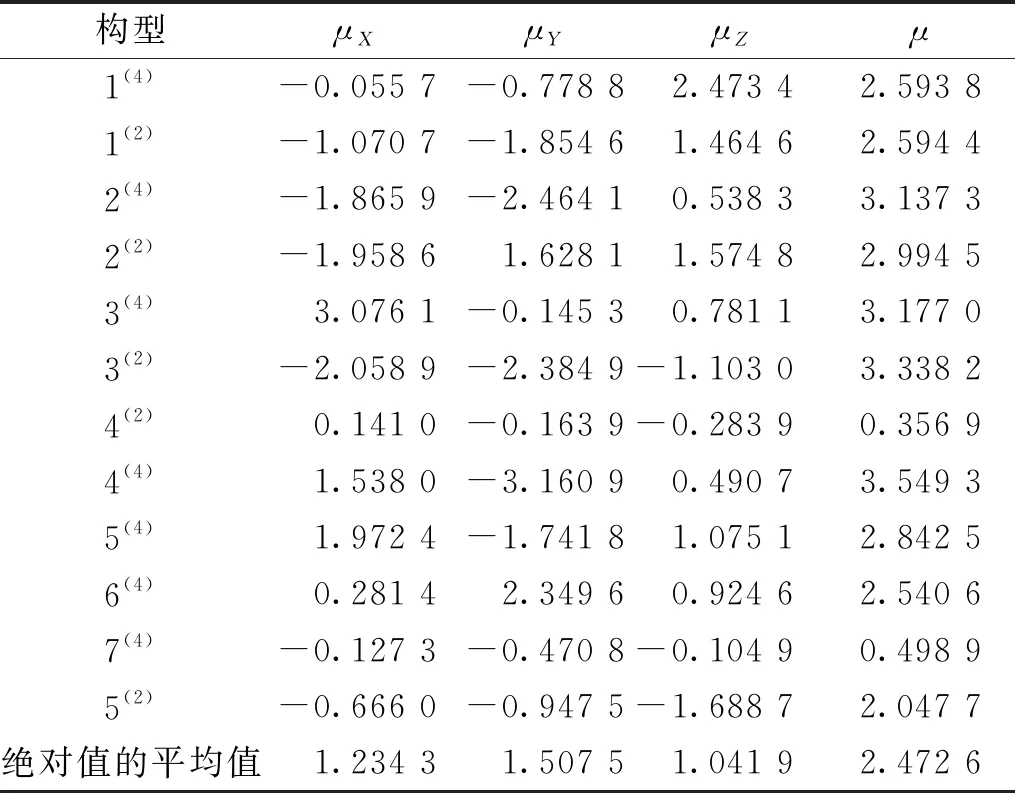
表2 团簇Co3NiB2 12种优化构型偶极矩 单位:D
分析表2数据可知:团簇Co3NiB2的12个优化构型在X、Y、Z方向上的偶极矩均不为0,说明团簇Co3NiB2所有优化构型均为极性分子。其中,构型4(4)的总偶极矩最大(3.549 3 D),说明该构型的分子极性最强;而与之相反的构型4(2)总偶极矩最小(0.356 9 D),表明该构型在团簇所有的优化构型中极性最弱。不难发现,团簇Co3NiB2所有优化构型的极性大小排序为:4(4)>3(2)>3(4)>2(4)>2(2)>5(4)>1(2)>1(4)>6(4)>5(2)>7(4)>4(2)。整体来看,X、Y、Z轴三个方向上的偶极矩数据绝对值的平均值满足Y轴(1.507 5)>X轴(1.234 3)>Z轴(1.041 9),说明在Y轴方向上正、负电中心偏移距离最大,Z轴正、负电中心偏移距离最小,这也就意味着Y轴对团簇Co3NiB2偶极矩的贡献最大,Z轴对团簇Co3NiB2偶极矩的贡献最小。
此外,偶极矩属于分子的静态性质,即在分子的点群对称下,偶极矩的大小和方向均不变,这也就意味着团簇的结构对称性也可通过偶极矩间接反映。将Gaussian 09程序计算所得的out文件输入Gauss View软件后可知,团簇Co3NiB2的12种优化构型的点群均为C1,这表明该团簇所有优化构型的偶极矩都位于各自构型的一重对称轴上。
2.4 团簇Co3NiB2轨道杂化分析
态密度(density of state,DOS)是能量介于E与E+dE之间的电子状态数目,一般用E表示,可用于表征电子结构的微观分布。分析态密度可以得到团簇的成键性质及团簇轨道的具体杂化情况。其中,总态密度(total density of state,TDOS)可用于表征各优化构型的总体电子分布情况,分波态密度(partial-wave density of state,PDOS)则可表征各优化构型单个原子中不同轨道的电子状态及贡献电子的能力。因此,通过分析图2中的总态密度图与分波态密度图可以得到团簇Co3NiB2轨道的杂化情况。图中的竖直虚线EF表示Fermi费米能级。
观察图2中各优化构型的总态密度图发现,团簇Co3NiB2所有优化构型均具有A、B、C、D、E 5个主要高峰,其中A、B均位于Fermi能级左侧,C、D、E均位于Fermi能级右侧。对各个峰进行具体分析发现:所有优化构型的A峰均由B原子的2s轨道贡献;B峰均由Co-3d、Ni-3d、B-2p轨道贡献,说明该峰存在d-d-p杂化,其中Co-3d、Ni-3d二者起主要贡献作用;D峰均由Co-4p与Ni-4p轨道贡献,说明所有优化构型的D峰均存在p-p杂化;而E峰则是均由Co-4s、Co-4p、Ni-4s、Ni-4p以及B-2p轨道贡献,说明该峰处存在s-s-p-p-p杂化,其中Co-4s、Ni-4s及B-2p起主要贡献作用。再对唯一不同的C峰进行分析发现:在四重态中,构型1(4)—4(4)均由Co-3d、Co-4p、Ni-4p及B-2p轨道贡献,说明它们存在d-p-p-p杂化,而构型5(4)—7(4)均由Co-4p、Ni-3d、Ni-4p及B-2p轨道贡献,说明这3种构型也存在d-p-p-p杂化,这也就意味着所有四重态构型的杂化方式均为d-p-p-p杂化;在二重态中,除构型5(2)与四重态构型1(4)—4(4)的杂化方式相同外,其余二重态构型1(2)—4(2)的杂化方式均一致,即所有二重态构型(除构型5(2)外)均是由Co-3d、Co-4p、Ni-3d、Ni-4p及B-2p轨道主要贡献,存在d-d-p-p-p杂化。

图2 团簇Co3NiB2各优化构型的分波态密度和总态密度
综上分析可知:团簇Co3NiB2的成键主要存在5种杂化方式,即p-p、d-d-p、d-p-p-p、s-s-p-p-p和d-d-p-p-p杂化,其中,p-p、d-d-p杂化作用较强,d-p-p-p、s-s-p-p-p、d-d-p-p-p杂化作用较弱。因此,可推断出p-p、d-d-p较强的杂化作用在促进团簇Co3NiB2成键形成的同时也增强了各优化构型的稳定性。与此同时,所有优化构型的A、B、D、E峰处的杂化情况完全一致,仅有C峰处的杂化情况因构型重态的不同而存在差异。其中,所有四重态构型的C峰处均是d-p-p-p杂化,所有二重态构型(除构型5(2)外)的C峰处均是d-d-p-p-p杂化,这说明C峰处的杂化情况会在一定程度上受团簇多重度的影响。
3 结论
本文以已构建出的Co3NiB2团簇模型为基础,通过结合构型能量与空间结构所得的团簇稳定性对其极化率、偶极矩及态密度方面进行微观理论的探究,最终得到以下结论:
1)从极化率张量平均值角度分析:团簇Co3NiB2的形变程度由大到小依次为:1(4)>1(2)>2(4)>5(4)>3(2)>2(2)>3(4)>5(2)>4(2)>6(4)>4(4)>7(4),即五棱锥构型>单帽四棱锥构型>单帽三角双锥构型>四角双锥构型,这与团簇Co3NiB2的稳定性排序一致,说明极化率对于团簇的几何结构具有很强的依赖性。
2)从极化率各向异性不变量角度分析:团簇Co3NiB2对外场的响应程度由强到弱依次为:2(4)>1(2)>1(4)>4(2)>2(2)>3(4)>3(2)>5(4)>7(4)>5(2)>6(4)>4(4),即单帽四棱锥构型>五棱锥构型>单帽三角双锥构型>四角双锥构型,这与2.1节中团簇Co3NiB2的稳定性排序相差不大,说明极化率各向异性不变量对于团簇的几何结构具有较强的依赖性,但依赖性不及极化率张量。
3)从偶极矩角度分析:团簇Co3NiB2所有优化构型均为极性分子,其中构型4(4)的分子极性最强,构型4(2)的分子极性最弱,且团簇Co3NiB2优化构型的极性大小排序为:4(4)>3(2)>3(4)>2(4)>2(2)>5(4)>1(2)>1(4)>6(4)>5(2)>7(4)>4(2)。其中,Y轴对团簇偶极矩的贡献最大,Z轴对团簇偶极矩的贡献最小。
4)从态密度角度分析:团簇Co3NiB2的成键主要存在p-p、d-d-p、d-p-p-p、s-s-p-p-p和d-d-p-p-p 5种杂化方式,其中,p-p、d-d-p杂化作用较强,d-p-p-p、s-s-p-p-p、d-d-p-p-p杂化作用较弱。与此同时,所有优化构型的A、B、D、E峰处的杂化情况完全一致,仅有C峰处的杂化情况因构型重态的不同而存在差异。其中,所有四重态构型的C峰处均是d-p-p-p杂化,所有二重态构型(除构型5(2)外)的C峰处均是d-d-p-p-p杂化,这说明C峰处的杂化情况会在一定程度上受团簇多重度的影响。

