基于天气类型及改进的小波神经网络的光伏发电短期预测
陈美珍,柳 扬,徐胜彬,郭俊锋,张永强,林金阳*
(1.福建工程学院 电子信息与电气技术国家级实验教学示范中心,福建 福州 350118;2.福建工程学院 微电子技术研究中心,福建 福州 350118)
随着人类对能源的需求逐渐增加,太阳能是现时期投入使用的重要的可再生能源,而光伏发电是利用太阳能的主要方式之一,由于太阳能光伏发电存在可变性和不确定性,会影响电力系统的功率平衡和安全稳定[1-4]。因此,为了保证电网的稳定运行,光伏发电预测是必须研究解决的问题。SHI等[5]提出应用径向基神经网络(radial basis function,RBFN)方法对第二天的每小时太阳能光伏发电预测,并且用支持向量机(support vector machine, SVM)进行分类。RAMSAMI等[6]提出了一种统计模型的混合模型,其中将基于人工神经网络(artificial neural network,ANN)的方法与自回归综合移动平均(autoregressive integrated moving average model,ARIMA)方法相结合,用于太阳能预测。LEVA等[7]提出了一种混合模型,该模型结合了统计模型和太阳能光伏性能模型,可预测具有小时分辨率的太阳能光伏发电量。
在文献[7]中,将人工神经网络方法与辐照度,发电量和数值天气预报(numerical weather prediction,NWP)的每小时历史数据一起应用,以预测未来24 h的每小时光伏发电量。HOSSAIN等[8]提出了一种基于极限学习机的预测模型,用于按小时分辨率进行日前光伏发电预测。ZHANG等[9]提出了一种集成方法,使用多个气象和天文数据进行小时日前太阳能光伏发电预测。在文献[9]中,比较了四种最先进的预测方法,即k近邻(K-NearestNeighbor,KNN),ANN,支持向量回归(support vector regression,SVR)和分位数随机预测方法在未来24 h内的性能。GIGONI[10]、刘沛汉[11]、刘爱国[12]、冬雷[13]等采用遗传算法结合神经网络,提高了网络全局寻优的能力,一定程度上提高了预测的精准度。
本文在划分天气类型的基础上,首先,综合研究分析各气象影响因子对光伏预测的影响;其次,计算出对光伏输出的主要影响因子,并将其作为预测模型的输入;最后,建立布谷鸟优化小波神经网络预测模型(cuckoo search algorithm optimized wavelet neural network,CS-WNN),布谷鸟优化算法(cuckoo search algorithm,CS)可以解决由于小波神经网络(wavelet neural network,WNN)易陷入局部最小值造成网络结构不稳定的问题,并且另外建立4个不同的预测模型进行仿真对比分析,模型仿真结果表明,本文提出的方法相比其他预测模型,具有更高的预测精度。
1 光伏预测的影响因素
1.1 光伏发电站与数据
本文研究场站为江苏某光伏场站,数据采用了2017年全年的光伏输出数据和气象数据,该数据实时记录了全天24 h每15 min的监控数据。
1.2 气候对光伏输出的影响
光伏输出与许多气候因素有关,如温度、湿度、辐照度、大气压力等,这些气象数据都可能对光伏输出产生影响,所以必须分析这些气象因素与光伏输出的关系。对气象数据和历史输出数据归一化处理,画出气象因素和光伏发电输出的关系曲线作对比,如图1所示,本文提取的是2017年1月1日5:00—19:00气象数据及光伏输出数据,从图1(a)中可看出太阳辐射随时间的变化曲线与光伏输出的变化曲线非常相近,因此太阳辐射对光伏输出具有很大的影响力,并且二者成正相关关系;而图1(d)中,湿度的变化曲线与光伏输出的变化曲线成负相关的关系;图1(c)和图1(d)中温度、气压分别与光伏输出只有一段时间的曲线较为接近,由图形无法准确得出他们之间的关系,这是因为影响光伏输出的因素有很多,并且各个因素之间又有着紧密的联系,而且在预测中无法对所有因素全面考虑,从而减小了预测光伏电站光伏输出的精度。因此本文采用Pearson相关系数法来计算光伏输出的主要影响因子,将图形和Pearson相关系数计算结果结合考虑,最终得出影响光伏输出的影响因子。

图1 气象因素与光伏输出的关系
在统计学,Pearson相关系数表示的是两个变量之间线性相关的关系,两个变量之间的Pearson相关系数定义为两个变量之间的协方差和标准差的商[14]:
(1)
上面的方程定义了总体相关系数,估计样本的协方差和标准差,就可以得到皮尔逊相关系数r。
Pearson相关系数的计算公式如式2所示:
(2)
对影响光伏输出的4个影响因素进行Pearson相关系数计算,如表1所示。

表1 Pearson相关系数
通过数据分析图和Pearson相关系数可以得出结论:太阳辐照度、温度、湿度是影响光伏输出的主要影响因素。
1.3 天气类型对光伏输出的影响
影响光伏输出的因素很多,天气类型是影响光伏输出的重要影响因素之一,描述天气类型的方法众多。本文依据2008年中国气象局发布的《公共气象服务—天气图形符号》(GB/T 22164—2008)中的气象类型来定义本文的天气类型,以此来统一天气类型的定义。如图2所示是某场站2017年一整年的天气类型,从图中可看出该场站一年中主要的天气类型为多云、雷阵雨、晴、小雨、阴、阵雨,其他类型的天气类型所占比例很小。基于典型天气代表以及本文研究地点的考虑,本文共划分6种天气类型,分别为多云、雷阵雨、晴、小雨、阴、阵雨。

图2 场站所在地天气类型
1.4 季节类型对光伏输出的影响
不同的季节有各不相同的太阳的入射角、光照的强弱以及日照时间,在不同的季节中,到达地面的辐照强度也会不同,光伏发电输出功率会随着太阳辐照强度的改变而变化。不同季节类型所对应的光伏输出的变化曲线如图3所示。

图3 不同季节所对应的光伏输出功率变化曲线
图3是在同一个天气类型的基础上,不同季节对应的光伏输出功率的变化曲线,每个季节都具有基本相似的变化规律曲线,但其具体的功率的大小和时间范围是不同的,夏季时,光伏日照时间更长,发电时间也更长,但是输出值反而更小,且曲线波动大,这是由于夏季的气温高、湿度大、强降雨、恶劣天气相对频繁,这些夏季特有的因素都会对电站发电量造成一定的影响,通过对数据的分析发现,当光伏板的温度过高时也会影响光伏板的发电量,数据分析如图4所示。

图4 环境温度和组件温度对光伏发电功率的影响
图4是夏季时环境温度和组件温度对光伏发电功率的影响,为了便于观察,数据都进行了归一化处理。由图可知,环境温度与光伏发电功率密切相关,大约13:30时组件温度最大,此时发电功率与组件温度曲线距离开始变大,因此夏季时由于光伏板温度过大对发电功率产生一定的影响。相反冬季时的日照时间比较短,但光伏输出值更大,这也是由于该场站属于南方,没有大雪等恶劣天气的影响,光伏输出曲线反而非常平稳。所以季节类型对光伏输出存在一定的影响。
2 神经网络以及算法
2.1 基于小波神经网络
WNN是结合了小波分析和神经网络的结构,拥有小波分析的时频性的优点和神经网络自学能力的优点,具有较强的非线性拟合能力和模式识别能力,对于非线性较强的光伏输出预测更为适用[15]。WNN模型描述如下:
(3)
式中,φ(K)为小波函数;I为输入层节点号;J代表隐藏层节点号;K为输出层节点数;wij为隐含层的权值;wjk为输出层的权值;J为隐含层节点个数;k为输出层个数,WNN结构图如图5所示。

图5 小波神经网络结构图
图5中X1,X2,…,Xn为小波神经网络的输入参数;Y1,Y2,…,Yn为小波神经网络的输出参数;wij,wjk为网络的权值。在输入信号序列为Xi,i=1,2,…,k时,隐含层输入公式为:
(4)
式中,h(j)为隐含层中第j个节点输出值;wij为输出层和隐含层的连接权值;hj为小波基函数;bj为小波基函数hj的平移因子;aj为小波基函数hj的伸缩因子;l为隐含层个数。
本文选用 Morlet函数为小波基函数,具体公式如下:
y=cos(1.75x)e-0.5x2
(5)
小波神经网络输出层计算公式为
(6)
式中,wik为隐含层与输出层直接连接权值;h(i)为第i个隐含层节点的输出;l为隐含层节点数;m为输出层节点数。
2.2 布谷鸟算法
CS算法是一种新兴启发算法。通过布谷鸟不筑巢将蛋产在别的鸟类鸟巢的行为得到启发,布谷鸟会从一个鸟巢随机飞到另一个鸟巢,以寻找寄主的鸟巢候选者,然后,选择最佳的巢,以使它们的鸟蛋有最佳的孵化机会并产生新一代的布谷鸟。CS算法的本质就是通过更新鸟窝的位置来达到寻求最优解的目的,存活下来的鸟蛋就是最优解[16]。
在CS算法中,布谷鸟的飞行行为是Lévy飞行。Lévy飞行意味着动作或飞行的步长将遵循Lévy分布,而随机步长为levy分布:
Levy:μ=t-λ,1≤λ≤3
(7)
(8)

布谷鸟优化算法具体流程如图6所示。

图6 布谷鸟搜索算法流程图
2.3 预测模型总体框架
预测模型总体框架如图7所示。
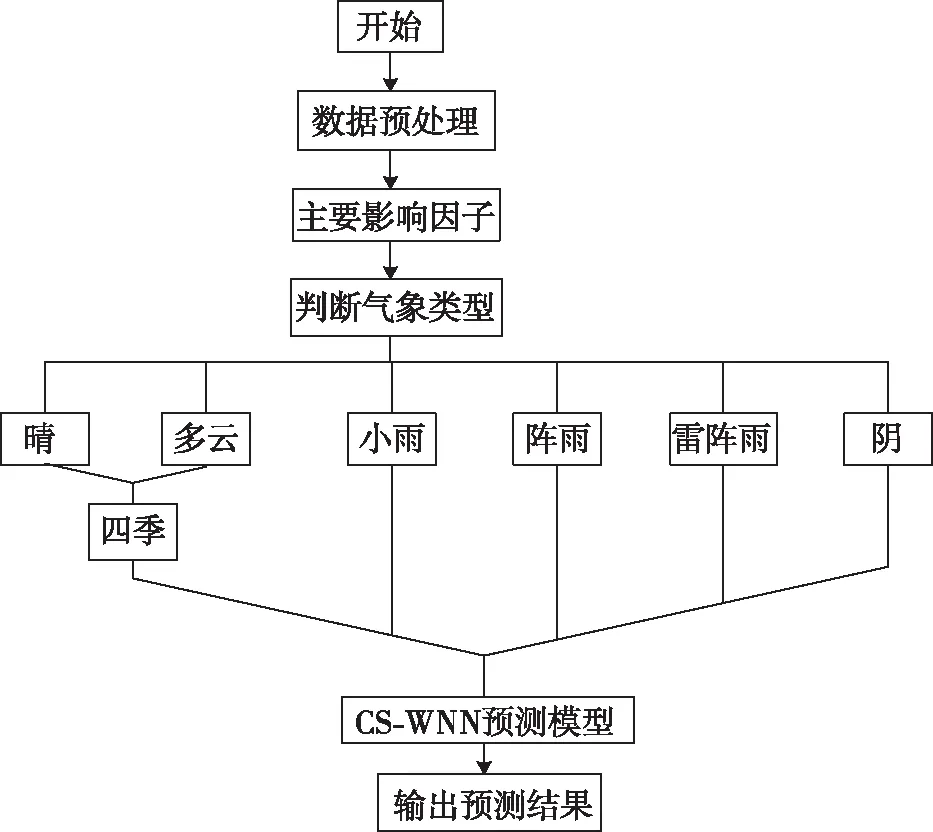
图7 预测模型总体框架
3 仿真分析
3.1 光伏发电功率预测
首先根据江苏省某场站6月份数据计算气象影响因子的皮尔森相关系数,从而得出光伏输出的主要影响因子为:温度,湿度,辐照度。本文利用MATLB作为程序开发环境,输入层为3,输出层为1,隐含层为6,以温度,湿度,辐照度作为预测模型输入层的特征向量,输出为光伏输出。
研究表明,季节对光伏输出也存在一定的影响。对场站数据进行分析,该场站数据为一天24 h每间隔15 min一条数据,一年中,每个天气类型的数据量不同。通过对数据的处理和筛选,除晴天与多云两种天气类型外,其他4种天气类型天数少,分布集中,甚至雷阵雨都集中在夏季,所以这4种天气类型的训练样本都在预测模型中直接训练,而晴天与多云两种天气类型在一年中分布较广,数据多,为了增加预测的精确度,将这两种天气类型在基于季节的分类下建模预测。
从科学的角度来看,四季应以二分二至划分,即以春分、夏至、秋分、冬至作为四季的起点和终点,为了便于计算,本文将一年12个月平均分为4等份,春季为3月—5月;夏季为6月—8月;秋季为9月—11月;冬季为12月—2月。
根据天气类型以及四季,分别抽取2017年1月1日(多云冬),2017年1月9日(晴冬),2017年3月12日(小雨),2017年3月27日(晴春),2017年5月1日(多云春),2017年6月2日(多云夏),2017年7月25日(晴夏),2017年8月1日(阵雨),2017年8月24日(雷阵雨),2017年9月8日(晴秋),2017年11月28日(多云秋),2017年12月30日(阴),共计12天的气象和光伏输出作为测试样本。
为了准确评价CS-WNN预测模型的预测效果,本文同时建立了WNN神经网络模型,BP神经网络模型,遗传算法优化BP神经网络的预测模型(genetic algorithm optimization bp neural network,GA-BP),遗传算法优化小波神经网络模型(wavelet neural network model optimized by genetic algorithm,GA-WNN)进行对比仿真试验,仿真结果如图8-9所示。
3.2 结果分析
图8为不同季节多云天气时5种预测模型的预测结果,从图中可以看出即使是同种天气类型,不同季节的光伏输出变化是不同的,从而验证了分不同季节来预测光伏输出的必要性。

图8 多云天气四季的的预测结果
从图8、图9可以看出,5个预测模型都能大致地描绘出实际光伏输出的变化曲线,当光伏输出曲线波动较大时,如小雨和阴天,5种模型的预测效果明显变差。从图8的4个模型可以看出对预测日在四季的基础上进行预测时,预测效果明显更好,并且变化曲线也相似。无论针对哪个天气类型,CS-WNN、GA-WNN模型明显优于GA-BP模型、BP模型和WNN模型,但是CS-WNN与GA-WNN两种预测模型曲线变化趋势与实际都较为接近,凭肉眼无法准确评价两个模型的预测效果,为了更好地评估对比预测效果,采用均方根误差(RMSE)与绝对系数(R2)作为评估指标,RMSE和R2的计算公式如式所示:
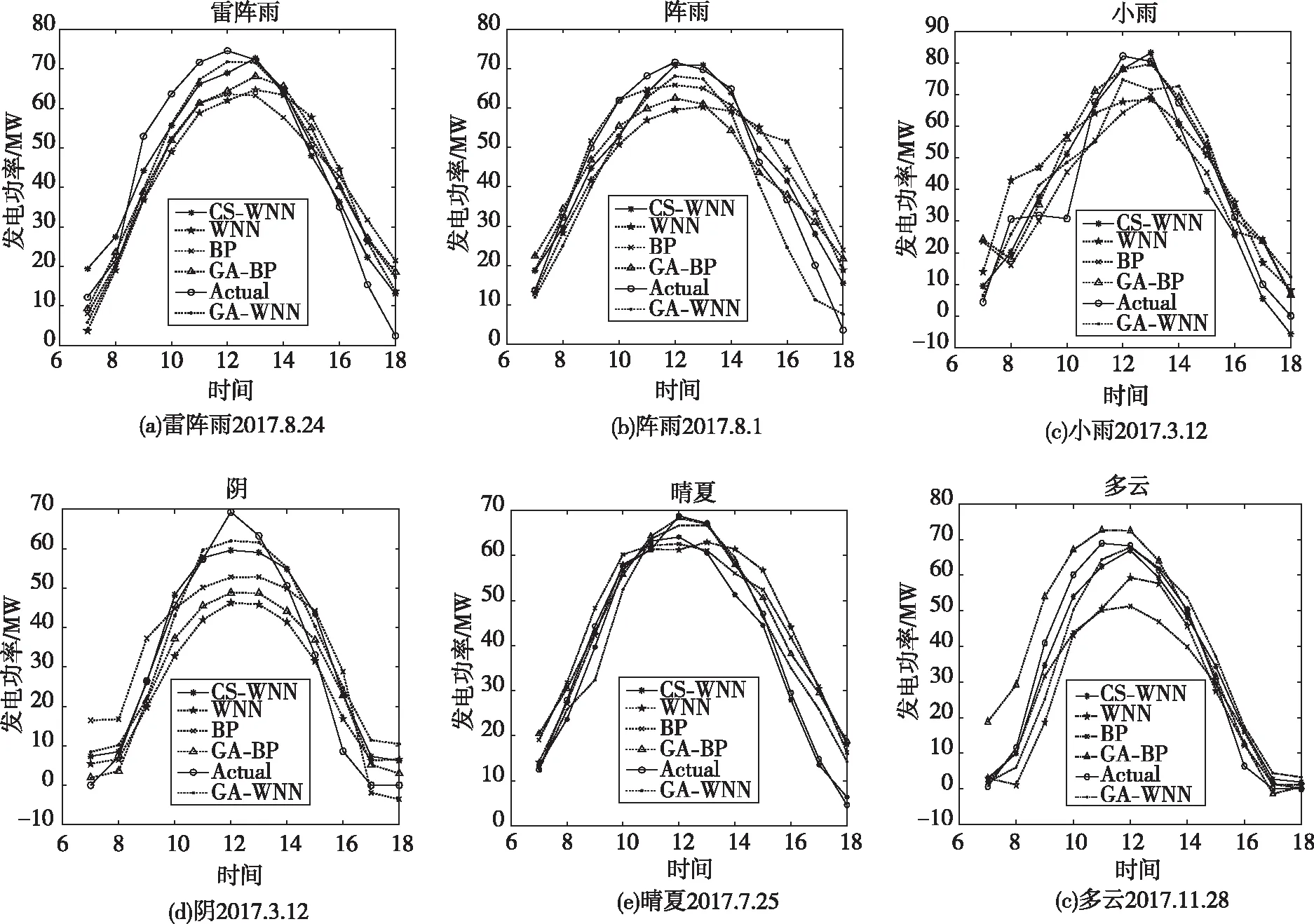
图9 6种天气类型预测结果
(9)
(10)

表2和表3是5种算法在多云时四季的预测效果,分别对应2017年5月1日(多云春)、2017年6月2日(多云夏)、2017年9月7日(多云秋)、2017年1月1日(多云冬)。通过观察比较表2和表3可以看出,5个预测模型对不同季节预测效果存在差异,CS-WNN的两个评价指标都更高,多云天气再针对四季预测光伏输出时,预测精度都很高。表3是5种算法在6种天气类型下的预测效果,多云和晴天都有在基于四季的基础上建立模型,它们的评价指标取四季的平均值,对比表2和表3,可看出雷阵雨,阵雨,小雨,阴这4种天气类型下预测精度都比较低,这是由于这4种天气是波动极端天气,而且没有再分四季,模型更难预测,所以预测精度更低。通过观察图8、图9可以发现CS-WNN模型、GA-WNN模型的拟合效果明显优于另外三个预测模型,表2和表3也论证了这一点,WNN、BP、GA-BP的平均R2值分别为0.821 8、0.814 6、0.861 9,而CS-WNN、GA-WNN的平均R2模型为0.904 8和0.932 4,虽然GA-WNN的预测效果也很好,但是CS-WNN的精度明显更高,5个预测模型中CS-WNN的RMSE值也是最低的。因此,相比其他模型,CS-WNN模型具有良好的预测精度和稳定性,但是由于光伏发电功率具有波动性和随机性,预测效果都会存在一定的偏差。

表2 多云天气时5种模型四季预测结果对比

表3 不同天气类型5种模型预测结果对比

续表
4 结论
本文以江苏某光伏发电站为研究对象,分析了对光伏发电输出的主要影响因子,采用Pearson相关系数显著性检验,得到气象因素与光伏发电因素的相关程度,在基于天气类型的基础上筛选出温度、光照强度以及湿度作为预测网络模型的输入变量,在季节类型的基础上通过布谷鸟算法优化小波神经网络的预测模型进行预测,并且和传统的BP神经网络,WNN神经网络,GA-BP神经网络,GA-WNN神经网络进行对比。经过仿真试验证明,布谷鸟优化小波神经网络的预测效果较好,并且高于经典优化网络GA优化BP神经网络和GA优化WNN神经网络。但是由于光伏输出波动性、随机性、间歇性的特点,预测模型有待进一步优化来提高预测精度。该模型在光伏发电预测领域提供了一种新的方法,具有较好的理论应有价值与市场应用价值。

