关于两个爆破设计公式的思考与改进

丁汉堃，石磊，西子阳

(北京中科力爆炸技术工程有限公司， 北京 101318)

根据长期从事爆破设计与施工的经验，有意识地体验参数与现场的差距，预估与现实爆破效果的差距，思考问题根源，其中设计所选用公式是否合理是产生问题的原因之一。因此，结合爆破理论、爆破设计公式进行了分析研究，认为存在不足。一是公式建立的理论基础不合理，二是应用结果与实际有较大差距。鉴于以上情况，作者对爆破设计公式进行解析，指出其中的不足，并提出改进意见。

1 两面临空爆破设计公式分析

1.1 理论分析

集中药包处在两面临空状态时，文献[1]提供的设计公式为：

式中，Q1，Q2为两侧等效子药包药量，kg。

上述推导结果说明，当子药包药量相等时，公式（1）才能成立，也可以说，无论两侧的W值、n值如何变化，集中药包的子药包的药量永远是平均分配的。这种假设推导出的公式（1）是值得商榷的。两面临空岩体两侧呈现不同的运动状态，不是由子药包药量相等决定的，而是由两侧岩体所获动量相等决定的，即由不同大小的岩体所获不同的速度决定的。大多数为Q1≠Q2，而Q1=Q2只是其中特例。

式（1）中f(n)没有指出具体函数式，在利用f(n)=0.4+0.6n3计算时，n值会出现负值，是无意义的情况。因此，式（1）不适合爆破设计应用，应考虑重新建立新的公式。

文献[2]指出，炮孔内爆炸气体对抛体做功，根据动量守恒定理，气体作用于药室气腔内壁的冲量等于抛体获得的动量，进而推出公式：

式（7）～式（9）说明，推导出的子药包药量与抵抗线关系式正符合爆破能量分配规律，即抵抗线小获得能量大，进而抛体的速度大、位移大，产生抛掷的爆破效果。反之，抵抗线大，获得能量就小，进而抛体速度小、位移小，自然就产生松动的爆破效果。只有W1=W2时，Q1=Q2才能成立，是本公式的一个特例。

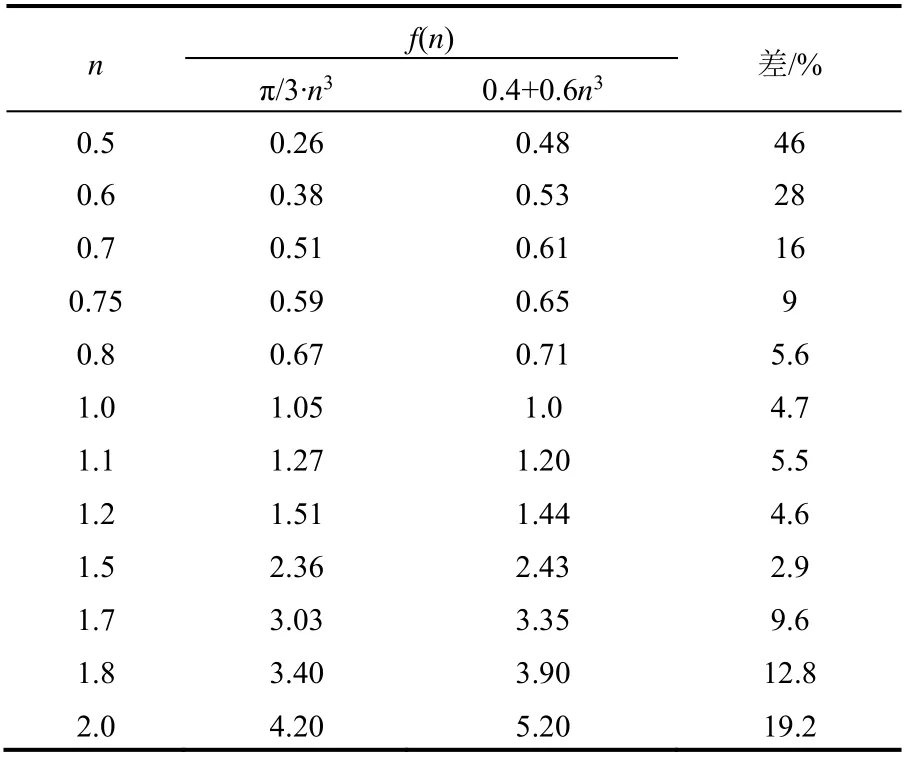
表1 n-f(n)关系

1.2 工程实例

两面临空地形硐室爆破，一侧要求抛掷爆破，另一侧为松动爆破。

基本参数：

子药包1：

W1=10 m，n1=1.2，k0=1.5 kg/m3，Q1未知。

子药包2：

W2=15 m，n2未知，k0=1.5 kg/m3，Q2未知。药包：Q未知。

由式（12）可得n2=−0.65。n为负值无意义，以下参数无法计算。

2.1 露天爆破设计公式分析

2.1.1 理论分析露天爆破在设计施工中广泛使用的公式是Q=qabH。实践证明，用此公式计算结果与实际施工存在较大差距，有必要指出此公式不足之处，分析原因，提出改进意见。

泵站设置在涝河渠道左岸，采用立式管道离心泵。涝河滩地片区与贤庄周围片区管线在泵站上游分开，两片区进行分组轮灌，各管道设置控制阀，以控制管道水流方向。两片区均采用一级干管布置，干管设给水管，田间为当地自备软管灌溉。

式中，Q为单孔药量，kg；q0为单耗，kg/m3；a为孔间距，m；b为孔排距，m；H为台阶高度，m。

式（13）可以变换成（装药结构详见图1）：

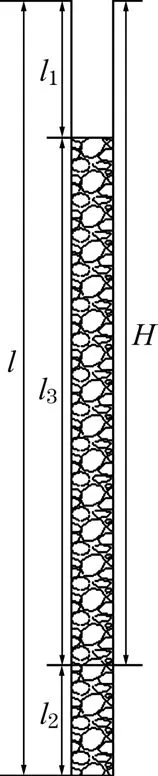
图1 装药结构

或

式中，l为孔深，m；l1为堵塞长度，m；l2为超深，m；l3为超深以上装药长度，m。

分析式（14）、（15）存在以下问题。

（1）超深部位的药量没有计算在内。应该装药的位置没有装药。

（2）堵塞部位计算了药量。不该装药的位置却装了炸药。

由于存在以上问题，用式（13）计算出的药量或多或少以致堵塞长度或短或长，造成炮孔装药结构不合理，给现场作业造成困扰，见表2。

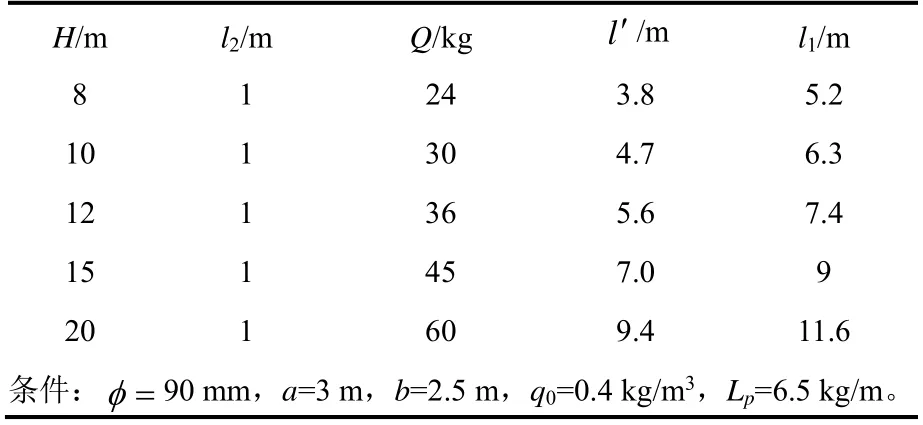
表2 运用Q=q0abH 计算参考值

笔者认为式（13）中的单耗q0为综合单耗。在工程预算、工程投标、工程成本核算等项目中，式（13）中的单耗q0是可以应用的。

在以式（13）为基础的常规设计中，常以单耗q0为不变量求出药量，但实际上单耗q0是随孔深变化的。笔者认为钻孔爆破不变量是炮孔线装药密度Lp，见图2、图3。

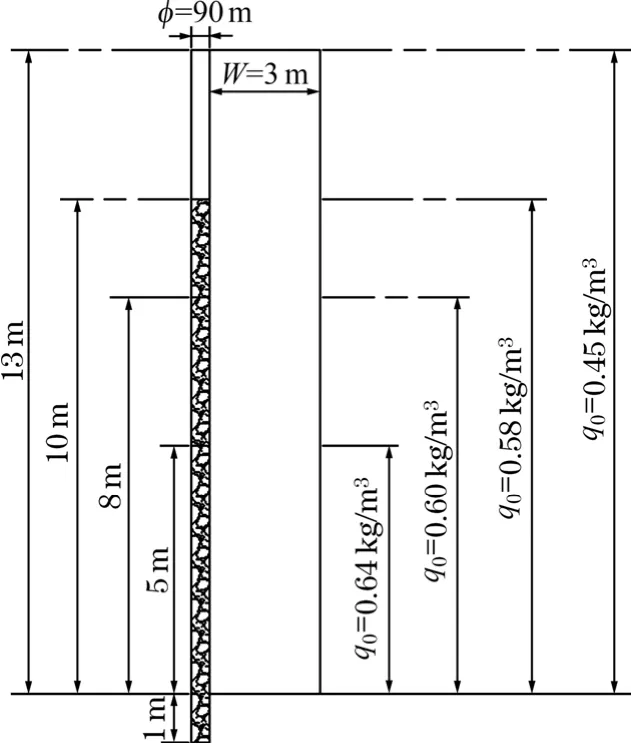
图2 公式Q=q0abH 中l～q0 关系

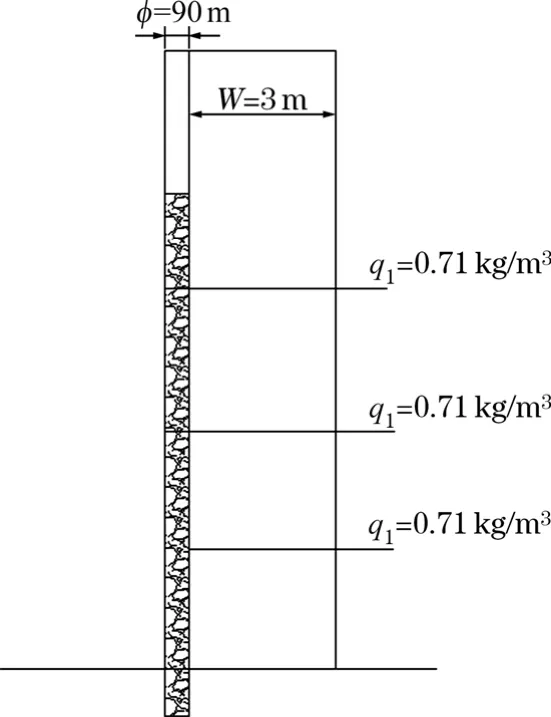
图3 公式Lp=q1W 2 中l～q1 关系

式（13）是以岩体爆破后形成矩形柱体而推导出来的，而实际上岩体爆炸后形成的是三角形柱体，由此而推导出来的公式是Lp=q1W2，强调在线装药密度Lp一定的前提下，抵抗线W与条形药包单耗q1的关系，其中q1是直接决定岩体运动状态以及影响爆破质量的重要参数，也可称为设计单耗。

为了改变式（13）计算药量与现场装药量差距较大的情况，在上述分析的基础上，调整爆破设计程序使得各参数符合实际，以提高药量计算的准确性。

设计程序以线装药密度为基础，优先确定炮孔装药结构，推导其他参数，最后计算综合单耗。

以温岭山体爆破工程为例，设计参数见表3～表6。

表3 基础参数

表6 综合参数

其中：抵抗线按经验公式确定：

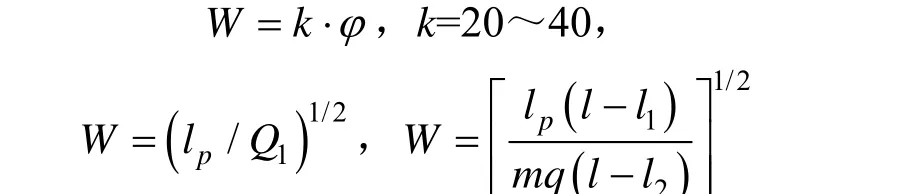
式中，q1为条形药包单耗，kg/m3；q1=[(l−l0)/(l−l1)]·m·q0；m为炮孔密集系数。

表4 装药结构参数

表5 孔网参数

2.2 实施效果

上述工程实例数值仅为多项爆破工程中的一项。在采用Q=q0abH公式设计施工时，计算出的药量或多或少致使施工时常发生退药或缺药的情况，给装药作业、库房管理造成很大影响。有时也发生装药不到位或堵塞过长的情况，影响了爆破效果。以线装药密度为固定值改进设计方法后，现场爆破施工主要表现在设计参数贴合实际，依据趋于科学，现场装药结构合理。依据公式Q=(L−n1·l1)Lp（L为炮孔总长度）计算爆破作业总用药量更为准确，有效减少了以前存在的不良现象。

3 结语

根据爆破工程实际的体验，对两个常用的爆破设计公式进行详细的解析，指出了其中的不足并提出了改进意见，其中集中药包在两面临空条件下，等效子药包的药量分配公式填补了设计公式的缺憾，改进了钻孔爆破的设计程序，使爆破设计更加合理，工艺参数更加实用，可对相关爆破工程设计施工提供参考指导作用。