真三轴加卸载下砂岩力学特性的速率效应

刘双飞

(1.安徽水利开发有限公司，安徽 蚌埠市 233000；2.安徽建工嘉和建筑工业有限公司，安徽 蚌埠市 233000)

0 引言

岩土工程开挖过程中，岩石在应力重新分布时多表现沿开挖工作面的应力卸荷，发生明显的卸荷变形[1−3]，当岩石聚集的能量快速释放，可能引发岩石突然间的整体失稳破坏[4−5]。近年来，众多学者针对岩石的速率效应进行了大量研究，取得了很多有意义的成果。黄达等[6]通过对大理岩进行9 种不同应变率的单轴试验，研究发现随着加载应变率的增加，岩样破裂模式由张剪型逐渐过渡到张型劈裂甚至劈裂弹射；藕明江等[7]分析了不同卸荷速率下岩爆碎屑破坏特征，发现卸载速率越大，岩爆越剧烈，破坏碎屑的分形维值越大；丛宇等[8]利用室内试验与PFC 模拟试验，发现高卸载速率下模型内部会出现多条贯通性破坏面，次要破坏面明显，张拉破坏裂纹分布面积较高，但剪破坏裂纹较少；李建红[9]研究了不同围压卸载速率下岩石的声发射及损伤特征，发现卸载速率越大，煤岩的损伤发展越充分、越缓慢，两者呈良好的幂函数关系，且卸载速率大小决定了声发射整体趋势；刘永茜等[10]基于煤体常规三轴瓦斯渗流实验发现围压卸载速率越高，I 类和II 类裂隙越发育，裂隙发育能耗与卸载速率之间呈对数关系；姜德义等[11]研究了盐岩扩容损伤与围压卸载速率的影响，建立扩容与损伤关系模型，并用速率补偿因子对公式进行修正；王超圣等[12]研究加载速率对岩石强度、c、φ值的影响，并基于弹性能建立卸载速率影响系数；尹光志等[13]基于砂岩真三轴试验，引入应变偏应力柔量分析不同加卸载速率下砂岩变形规律，结果表明最小主应变和体积应变的偏应力敏感性与卸载速率呈正相关，最大主应变的偏应力敏感性与加载速率呈正相关，并讨论了卸载过程中能量变化的速率效；ZHAO X G 等[14]利用三轴应变冲击试验系统（配备声发射监测系统）对不同卸载速率下的应变冲击过程进行了研究，结果表明破坏过程中的剧烈程度和应变破裂过程中的声发射能量释放与卸载速率有关；LI X B 等[15−16]通过数值模拟试验研究卸荷速率对岩石试件卸载强度和破坏模式的影响，研究表明卸载速率越快，试件的卸载破坏过程越剧烈、速度越快，试件中劈裂裂纹越多。

以上研究表明岩石力学性质存在明显的速率效应，但自然界岩石多处于三维应力环境中，采用单轴、常规三轴试验获得的岩石特性存在一定的局限性。因此，本文在上述研究的基础上，开展不同加、卸载速率的真三轴试验，研究砂岩力学特性的速率效应，对岩土工程开挖的稳定性研究具有一定的工程价值和理论意义。

1 三轴压缩试验

1.1 试件制备与仪器

本次试验所用试件取自同一块均质性良好的砂岩岩块，试件为边长100 mm 的立方体，试样切割完成后，对其进行检查和打磨，确保试件表面平整，无明显缺陷，试件的长度允许误差±0.5 mm，试件面的平整度允许偏差±0.1 mm，垂直度的允许偏差±0.25°。

1.2 试验方案

为研究砂岩加卸载力学特性的速率效应，开展不同加、卸载速率的真三轴试验，应力路径示意图如图1 所示，试验方案分为两部分。

图1 应力加卸载路径

（1）加载速率试验。以1 kN/s 的速率加载应力至初始应力水平，σ1、σ2、σ3分别为70，50，30 MPa；σ2保持不变，以速率1 kN/s、2 kN/s、3 kN/s 加载σ1，以速率0.3 kN/s 卸载σ3直至试样破坏。

（2）卸载速率试验。以1 kN/s 的速率加载应力至初始应力水平，σ1、σ2、σ3分别为70，50，30 MPa；σ2保持不变，以速率3 kN/s 加载σ1，以速率0.1 kN/s、0.2 kN/s、0.3 kN/s、0.4 kN/s 卸载σ3直至试样破坏。

2 试验结果分析

本文以初始应力点为零点，对试验数据进行处理、分析，研究不同加卸载速率对砂岩力学变形特性的影响。

2.1 应力-应变曲线

图2 为不同加载速率下的砂岩应力−应变曲线。由图2 可知，不同加载速率下砂岩真三轴加卸载应力−应变曲线总体发展趋势大体相同，初期砂岩处于弹性变形阶段，应力−应变曲线接近于直线，达到弹性极限后，砂岩由弹性慢慢转化为塑性，曲线变缓，应变快速增大直至岩石破坏。加载速率对砂岩真三轴加卸载力学变形特性有着明显影响，随着加载速率的增大，砂岩应力−应变曲线直线段变长，斜率变大，岩石的弹性极限增大，弹性增强，同时岩石的抗压极限强度变大，最大主应变ε1与最小主应变ε3增大，但中间主应变基本保持不变，说明加载速率的提高，增强了岩石的弹性性能和承载能力，岩石加卸载方向变形发育更充分，但中间主应力方向变形基本稳定。图3 为不同卸载速率下的砂岩应力−应变曲线。由图3 可知，不同卸载速率下砂岩真三轴加卸载应力−应变曲线总体趋势大体相同，且与不同加载速率应力−应变曲线基本相同，说明不同的加、卸载速率不会改变砂岩变形破坏机制。同时，卸载速率对砂岩真三轴加卸载力学变形特性也存在明显影响，随着卸载速率的增大，砂岩应力−应变曲线近似直线段变短，斜率变小，岩石的弹性极限变小，弹性减弱，岩石的抗压极限强度变小，最大主应变ε1减小，而最小主应变ε3增大，中间主应变基本保持不变，说明卸载速率的提高，岩石的弹性性能减弱，抗压极限强度降低，岩石破坏时加载方向变形不充分，而卸载方向变形增大，中间主应力方向变形基本稳定。

图2 不同加载速率应力-应变曲线

图3 不同卸载速率应力−应变曲线

2.2 卸载过程曲线

图4 为不同加载速率时间−应变曲线。由图4可知，岩石应变ε1与ε3破坏前随着时间线性增大，在岩石破坏阶段，时间−应变曲线变陡，斜率变大，变形增大的越来越迅速。同时加载速率越小，加卸载破坏过程所用时间越长，且相同时间内，加载速率越大，ε1与ε3越大，说明加载速率越大，岩石破坏得越迅速，所需时间越少，破坏时应变越大。图5 为不同加载速率σ3−应变曲线。由图5 可知，岩石应变ε1与ε3初期随着围压的降低线性增大，随着σ3的减小，曲线越来越陡，应变随围压降低增大的越来越快。同时加载速率越大，曲线越陡，岩石应变随围压降低增大的越快，最终破坏时的σ3越大，说明加载速率增大，岩石变形加快，并在较大应力水平的情况下破坏。

图4 不同加载速率时间−应变曲线

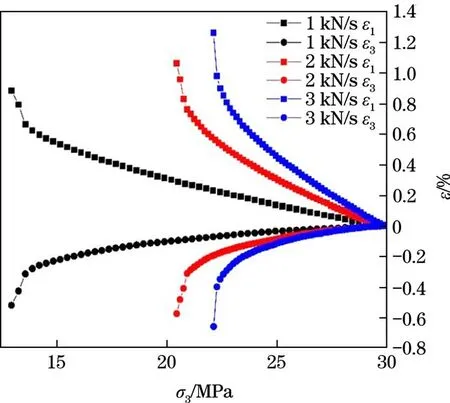
图5 不同加载速率σ3−应变曲线

图6 为不同卸载速率时间−应变曲线。由图6可知，应变ε1与ε3破坏前随着时间线性增大，在岩石破坏阶段，时间−应变曲线变陡，斜率变大，变形增大得越来越迅速。同时卸载速率越小，加卸载破坏所用时间越长，最终破坏时的ε1与ε3也越大，但相同时间内，卸载速率越大，ε1与ε3越大，说明卸载速率越大，相同时间内岩石变形越大，但卸载速率越小，岩石最终破坏时裂纹发育越充分。

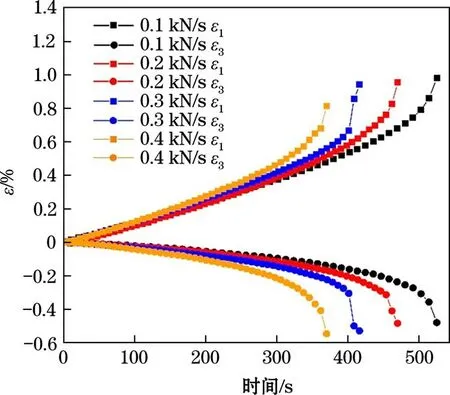
图6 不同卸载速率时间−应变曲线

图7 为不同卸载速率σ3−应变曲线。由图7 可知，岩石应变ε1与ε3初期随着围压的降低线性增大，随着σ3的减小，曲线越来越陡，应变随围压降低增大的越来越快。同时卸载速率变大，曲线平缓，岩石应变随围压降低增大的越慢，最终破坏时的σ3越小，说明卸载速率增大，相同卸载量所用时间变少，岩石裂纹发育不充分，岩石应变变小。

图7 不同卸载速率σ3−应变曲线

2.3 变形特征

以初始应力点为零点，为分析加卸载过程中岩石变形特征，定义变形模量E0为：

式中，σ1i为加卸载过程中任一点的最大主应力；σ10为初始最大主应力，70 MPa；ε1为以初始应力水平为零时对应的最大主应变。

图8 为不同加载速率变形模量−应变曲线。由图8 可知，不同加载速率下，岩石的变形模量随应变变化呈线性关系，变形模量随应变的增大而减小，加载速率越大，曲线越缓，变形模量随应变降低的越慢，说明在加卸载过程中，岩石变形模量逐渐劣化损伤，且加载速率变大，变形模量的劣化损伤变慢。加载速率v1=1 kN/s、2 kN/s、3 kN/s 时，变形模量的劣化幅度分别为52.6%、52.3%、55.3%，基本保持不变，说明加载速率的变化不会改变岩石加卸载破坏时的变形模量劣化程度。

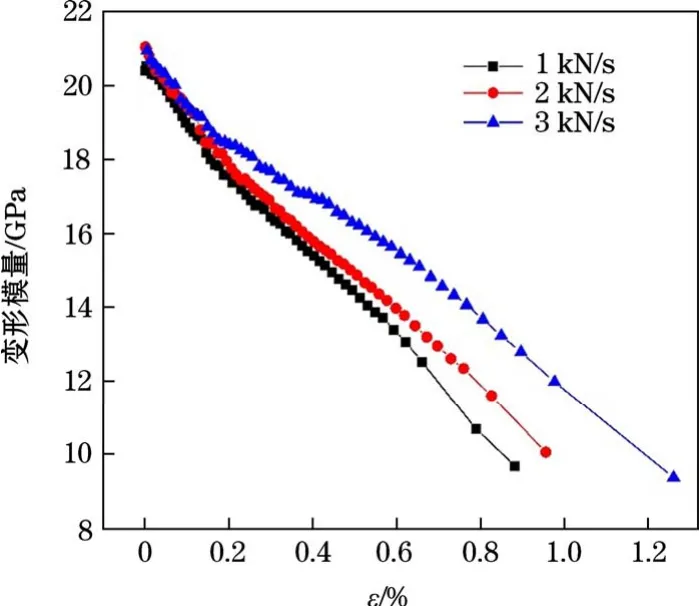
图8 不同加载速率变形模量−应变曲线

图9 为不同卸载速率变形模量−应变曲线。由图9 可知，不同卸载速率下，变形模量总体上随着应变的增大而减小，与不同加载速率下相似，但在加卸载前期差异较大。卸载速率v3=0.1 kN/s、0.2 kN/s 时，曲线近似为一条直线，当卸载速率增大至0.3 kN/s、0.4 kN/s 时，变形模量初期快速减小，而后曲线接近于直线，且在加卸载后期，卸载速率越大，变形模量越小，说明变形模量逐渐劣化，且卸载速率越大，加卸载前期变形模量劣化越明显，后期变形模量越小。卸载速率v3=0.1 kN/s、0.2 kN/s、0.3 kN/s、0.4 kN/s 时，变形模量的劣化幅度分别为45.1%、52.3%、49.5%、55.2%，表现为卸载速率越大，变形模量劣化幅度越大，岩石劣化损伤越严重，说明岩石变形模量对卸载速率较敏感，卸载速率越大，岩石裂化损伤越严重，岩石越容易破坏。

图9 不同卸载速率模量−应变曲线

3 结论

基于真三轴加卸载试验，研究了砂岩力学特性的速率效应，结论如下：

（1）随着加载速率的增大，岩石弹性增强，抗压强度增大，变形发育更充分；而随着卸荷速率的增大，岩石的弹性和抗压强度降低，破坏时加载方向变形不充分，而卸载方向变形增大；

（2）加载速率越大，岩石破坏时应力水平越高，破坏越迅速，所需时间越少，破坏时应变越大；卸载速率越大，相同时间内岩石变形越大，破坏时应力水平越低，但卸载速率越小，岩石最终破坏时裂纹发育越充分；

（3）加卸载过程中，岩石变形模量逐渐劣化损伤，加载速率变大、卸荷速率越小，变形模量的劣化损伤变慢。