多项式拟合的矿山企业安全投入产出分析

李亚军

(五矿二十三冶建设集团有限公司，湖南 长沙 410116)

0 引言

矿山安全事故会造成大量的人员伤亡与财产损失。为避免矿山安全事故，矿山企业每年都要投入大量的经费开展安全工作，但是，由于缺乏安全生产投入与安全生产产出之间的量化分析，往往存在安全生产投入太大，而安全生产产出绩效相对较小，或者安全生产投入太小而导致安全生产产出绩效较差的情况，即存在安全生产投入过剩或不足的情况[1]。为此，需要找到一个量化分析模型，对矿山安全生产投入与产出之间的关系进行精准量化分析，以最经济的安全生产投入取得预期的安全生产产出[2]。

对于安全生产产出的预测，以往采用单变量预测方法进行分析，一般以时间为自变量，以安全生产产出为因变量，利用灰色预测等各种预测模型进行安全生产产出预测，此类分析方法虽然在能在一定程度预测安全生产产出绩效的趋势，但却对安全生产投入没有考虑[3−4]。实际上，与安全生产产出绩效最密切相关的就是安全生产投入，脱离安全生产投入与产出绩效之间关系，就没有抓住问题本质，因而也就无法有效地对矿山安全生产工作做出指导[5]。

因此，需要建立精度较高的矿山安全生产产出与安全生产投入之间的量化分析模型，这对于科学指导矿山安全生产，尤其科学确定矿山安全生产投入是很有意义的。本文基于以往历年的矿山安全生产投入经费与矿山安全生产事故的经济损失及人员伤亡的数据，进行以安全生产投入经费为自变量，以安全生产事故经济损失、重伤人数以及死亡人数为因变量的预测，分别进行多次多项式拟合，并对各多次多项式拟合后的精度进行对比分析，优选出拟合精度最高的多次多项式；然后，根据矿山拟投入安全生产经费对矿山安全生产产出绩效预期进行分析，得出安全生产产出绩效达标情况下的最少投入的安全生产经费。该方法直面安全生产投入与产出的本质关系，为科学指导矿山安全生产经济性投入提供了新的方法。

1 系统建模

1.1 指标体系的构建

矿山安全生产投入包括多个方面，如劳保用具、安全设备、安全培训教育以及安全资料发放等归为安全生产经费的投入；表征安全生产绩效的因素指标也有多种，根据《职业健康安全管理体系规范》，安全生产绩效指标有经济损失、工时损失、轻伤事故率、重伤事故率及万人死亡率等，但工时损失明显也可以归为经济损失，轻伤事故一般情况下对矿山安全生产的影响相对较小。因此，结合《生产安全事故报告和调查处理条例》中对于安全生产事故等级的划分标准，选取经济损失，重伤人数及死亡人数作为安全产出绩效指标。

矿山安全生产投入产出系统见图1。

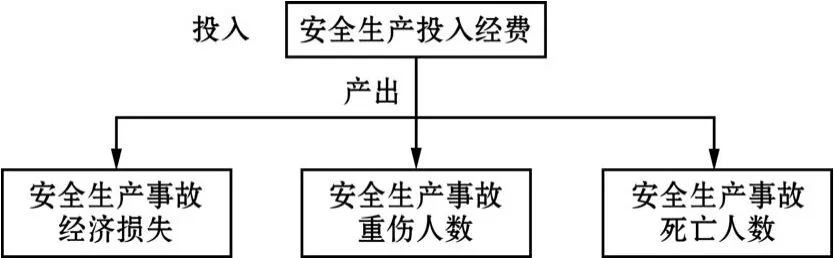
图1 矿山安全生产投入产出关系

1.2 多项式拟合

统计矿山历年的安全生产投入经费：X=(x1，x2，x3，…，xn)；历年的安全生产事故经济损失：Y=(y1，y2，y3，…，yn)；历年的安全生产事故重伤人数：Z=(z1，z2，z3，…，zn)；历年的安全生产事故死亡人数：W=(w1，w2，w3，…，wn)。根据安全生产事故经济损失、重伤人数及死亡人数与安全生产投入经费历年数据之间的对应关系，可以进行经济损失、重伤、死亡人数与安全生产投入经费之间的多项式拟合。以经济损失Y为例：

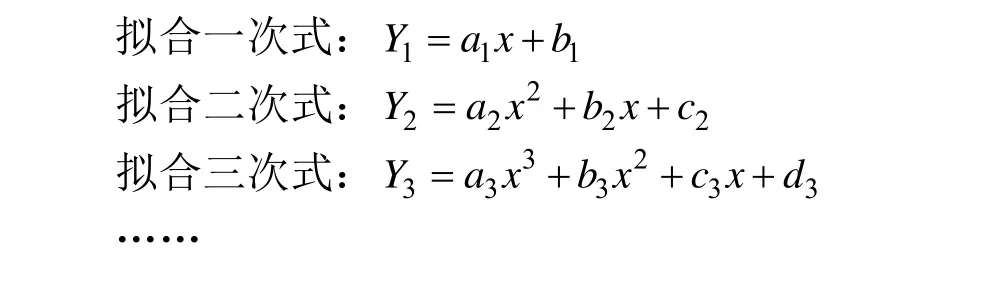
很显然，多次式的次数可以到无限，为控制分析的复杂程度，且根据实际经验，一般在5 次式以内，多项式就可以拟合到较高的精度，因此本次限定多项式拟合到5 次。

1.3 精度分析及多项式优选

得到残差平方和：

各拟合多项式的平均相对误差、残差平方和可以用来进行精度比较，以优选出精度高的多项式。根据矿山未来拟投入的安全生产经费，即可对相应的安全生产事故经济损失、重伤人数和死亡人数进行预测，以保证矿山安全生产不发生较大事故。

系统建模流程见图2。

图2 系统建模流程

2 例证分析

2.1 背景分析

选取某一成矿带上的有代表性的磷矿山企业，选取某些年份各矿山的安全生产投入产出情况进行分析：收集统计其安全生产投入经费、事故经济损失、事故重伤人数及事故死亡人数作为分析的基础资料，见表1。

2.2 多项式拟合分析

将表1 中的样本，按照安全生产投入经费升序排序，得到安全生产投入经费序列为X=(168，185，266，271，274，309，322，372，416，428，501，523)；对应得到安全生产事故经济损失序列Y=(1284，1207，844，831，779，589，602，518，211，203，129，113)，安全生产事故重伤人数序列Z=(18，19，14，15，14，12，13，11，7，8，5，4)，安全生产事故死亡人数序列W=(5，5，4，4，4，4，3，3，3，2，2，2)。将安全生产事故经济损失序列、重伤人数序列以及死亡人数序列与安全生产投入经费序列进行多项式拟合，得到5 次以内多项式拟合结果。

表1 矿山企业安全生产投入产出基础数据

（1）安全生产事故经济损失与安全生产投入经费的多项式拟合结果：

拟合二次式、拟合三次式、拟合四次式及拟合五次式的高次项常数均极小，可认为其不存在。

2.3 多项式拟合精度比较

由于安全生产事故经济损失与安全生产投入经费拟合的多项式有一次式和二次式，对两个多项式拟合结果根据式（1）～式（4）进行精度比较。比较结果见表2。

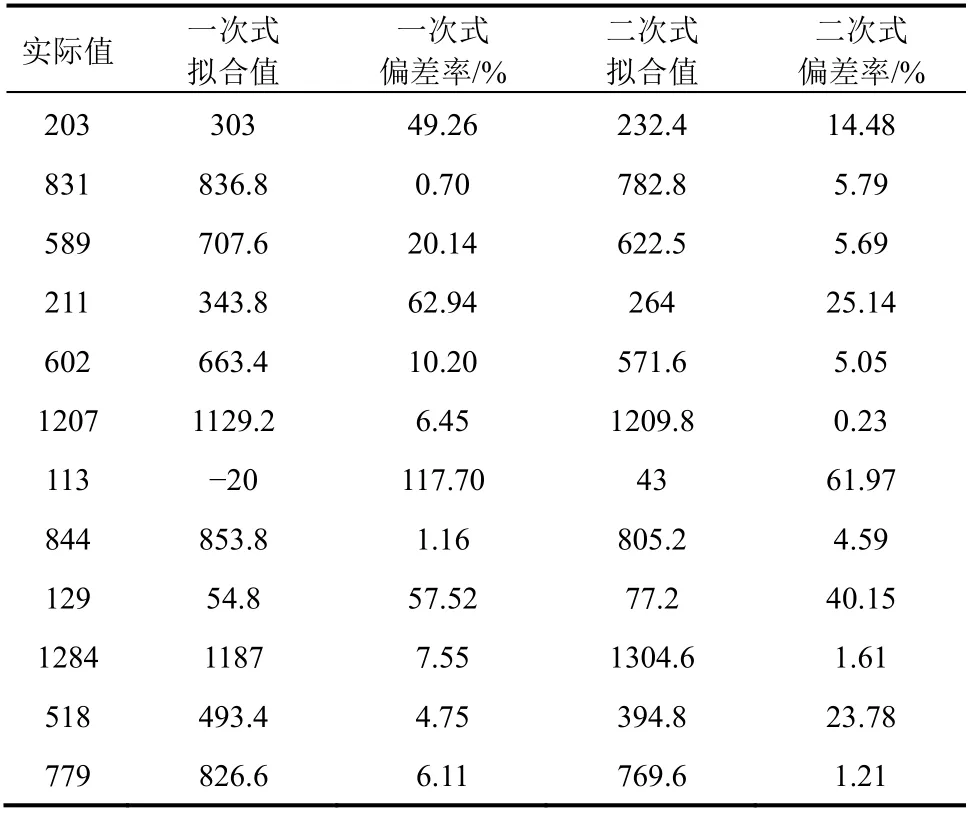
表2 安全生产事故经济损失拟合多项式精度比较

根据表2 中数据计算可得，一次式的拟合精度为71.29%，残差平方和为87 128.84；二次式的拟合精度为84.19%，残差平方和为32 830.54。说明对于安全生产事故经济损失与安全生产投入经费拟合而言，二次多项式无论是精度还是数据的波动性上均优于一次多项式。

故最终得到安全生产投入与产出拟合最优结果如下：

（1）安全生产事故经济损失与安全生产投入经费拟合的最优多项式：

（2）安全生产事故重伤人数与安全生产投入经费拟合的最优多次多项式：

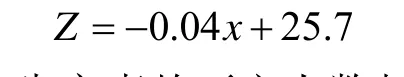
（3）安全生产事故死亡人数与安全生产投入经费拟合的最优多次多项式：

2.4 结果分析

现有A、B、C 三个矿山拟在2021 年投入安全生产经费分别为235 万元、412 万元及158 万元。经各安全生产产出的最优多项式计算，得到A 矿山2021 年的预计安全生产事故经济损失951 万元、重伤16 人、死亡4 人；B 矿山2021 年的预计安全生产事故经济损失275 万元、重伤9 人、死亡3 人；C 矿山2021 年的预计安全生产事故经济损失1362万元、重伤19 人、死亡5 人。根据《生产安全事故报告和调查处理条例》中对于安全生产事故等级的划分标准，预计2021 年A、B、C 三个矿山均会发生较大事故。

根据《生产安全事故报告和调查处理条例》对各安全生产产出的最优多项式进行反向推算。只有将矿山安全生产投入经费提高到445 万元及以上，才能保证矿山安全生产不发生较大事故。

3 结论

以收集统计的多个矿山多年的安全生产经济损失、重伤人数以及死亡人数等安全生产产出绩效及对应的安全生产投入经费为对象，采用多次多项式拟合进行关系分析，并对拟合得到的多个多次多项式进行精度对比优选，得到了最优多项式。根据最优多项式对投入的矿山安全生产经费进行计算，对矿山安全产出绩效进行了预计。该方法思路清晰、过程科学，可以考虑在相似领域中进行应用。

在采用该方法进行分析时，不仅可以根据矿山安全生产拟投入的经费对矿山安全生产状态进行预计；还可以反向推算出达到某种安全生产状态所需要的安全生产投入。