关于G-布朗运动驱动下随机卷积的一些结论
张 晶,王珠冉
江苏第二师范学院数学科学学院,江苏南京,210000
经济学中普遍存在的不确定现象使得线性概率和线性期望等常用数学模型失去用武之地,给不确定性分析带来困难。经过长时间的探索,Peng[1]提出新的次线性G-期望能够较好地解决这个基础性问题,弥补了线性概率空间的期望理论在经济学领域应用的不足。所谓的G-期望需要满足次可加性,即E(X+Y)≤E(X)+E(Y)。Peng根据G-期望构造出G-期望空间,随后构造出G-正态分布的理论,以及一种新的布朗运动{Bt}t∈[0,T],称为G-布朗运动。G-布朗运动和相应的 G-随机分析理论是分析金融市场中风险度量、递归效用理论和最优投资等更广泛的不确定性决策理论的基本工具,详见参考文献[2]。
此后,Ibragiomv[3]首次将G-期望从有限维空间引入无穷维空间,详细介绍了无穷维空间中G-正态分布随机变量的协方差集以及G-布朗运动驱动下的随机积分,并证明It等距不等式、B-D-G不等式、Fubini定理及随机卷积积分的连续性,借助随机卷积积分的性质给出完全非线性抛物型偏微分方程唯一粘性解的概率表示。值得关注的是 Ibragiomv没有给出随机卷积积分的Hölder连续性、有界性和极大值不等式,而这些性质在微分方程的应用中是非常重要的,本文将针对这方面问题做出补充。
目前,关于随机卷积积分的研究有大量成果,如Van等[4]系统地研究了随机卷积算子的R-有界性,建立L1-值有界性和X-值极大函数有界性之间的密切联系;Coupek等[5]专注于探究偏微分方程的时空正则性,通过有限域上巴纳赫空间随机变量的超压缩性结果,得到沃尔泰拉过程驱动下Lp-值随机卷积积分的Hölder连续性,以及偏微分方程解的相关正则性;Lv等[6]讨论了勒维过程驱动下随机分数阶热方程的随机卷积积分的 BMO估计、Morrey-Campanato估计以及方程解的p阶矩Schauder估计;Ondreját等[7]主要研究2-光滑巴纳赫空间中随机卷积积分的时间正则性,并以此为基础得到抛物型随机微分方程解的路径方程在时间上具有与维纳过程相同的正则性。近期随机卷积积分的极大值不等式也受到诸多学者的关注。在希尔伯特空间中,Salavati等[8]利用It-type不等式和B-G-D不等式得到鞅过程驱动下随机卷积积分的极大值不等式,该不等式满足p次幂的轨道有界,并给出不等式在非利普希兹条件下半线性随机演化方程方面的应用。在巴纳赫空间中,Zhu等[9-10]证明了补偿泊松过程驱动下随机卷积积分的极大值不等式,随后又研究在勒维过程驱动下B-D-G不等式和极大值不等式,得到随机卷积积分的指数估计,基于所得到的极大不等式,证明了勒维噪声驱动的随机偏微分方程温和解的存在唯一性。
在前人研究的基础上,文本结合无穷维空间中经典布朗运动驱动的随机卷积积分和G-布朗运动驱动的随机卷积积分的结果进行研究,使随机卷积积分的性质在无穷维G-布朗运动中更加完善。同时,采用因子分解法、B-D-G 不等式和酉扩张的方法,研究无穷维空间中G-布朗运动驱动下随机卷积积分的Hölder连续性、有界性以及弱极大值不等式,以期能为相关领域研究提供一定的参考。
1 预备知识
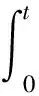
本节简要介绍文章中使用到的一些概念和性质,包括次线性空间、G-布朗运动及常用的不等式。想要更深入了解关于次线性空间和G-期望的更多相关知识请参阅文献[1]和[3]。
定义1[3]设Ω是给定的非空集,ћ是定义在Ω上实值向量集的函数,泛函E :ћ→R。如果对任意的X,Y∈ћ满足以下条件:
(a)单调性:若X≤Y, 则E(X)≤(Y);
(b)保常性:若c∈R,则E(c)=c;
(c)次可加性:E(X+Y)≤E(X)+E(Y);
(d)正齐次性:若λ> 0,则E(λX)=λE(X);
则泛函E称为次线性期望,称(Ω,ћ,E)是次线性空间,如果只满足(c),(d),则称E为次线性泛函。
定义2[3]对于任意时刻t≥ 0,若X是次线性期望空间(Ω,ћ,E)上的随机变量,则称Xt:Ω×R+→X为随机过程。
定义3[3]若随机过程{Bt}t∈[0,T]满足以下条件:
(1)B0=0;
(2)平稳增量性:对任意的t,s≥0,增量(Bt+s-Bt)与Bs同分布,即(Bt+s-Bt)~NG(0,sΣ);
(3)独立增量性:对任意的t,s≥0,增量(Bt+s-Bt)关于(Bt1,Bt2,…,Btn)独立,其中n∈N,0≤t1≤t2≤…≤tn≤t。
则称{Bt}t∈[0,T]为G-布朗运动。
为了能够让读者更加顺畅了解本文的研究内容,接下来介绍一些关于无穷维空间中G-期望的基础知识。
假定U,H是希尔伯特空间,算子Φ在H上且domΦ=UΣ⊂U,定义范数
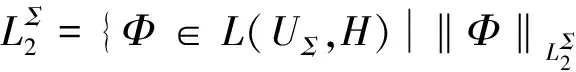
为了便于读者阅读,下面给出本文中需要用到的空间符号表示。
(1)L(U,H):={Φ:U→H|Φ是线性且连续的};
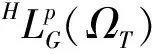
引理1[3]若随机变量X服从均值为0,方差为Σ的G-正态分布,Σ是协方差集,记为X~NG(0,Σ),我们有如下估计,对任意的m≥1,
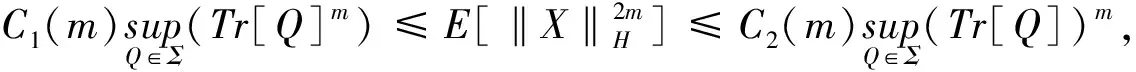
引理2[3](It等距不等式)令Φ∈HM2,0G(0,T),则有
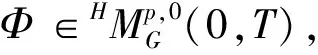

以上三个定理主要应用于第二部分随机卷积积分性质的证明过程中,引理1说明服从G-正态分布的随机变量X有限阶矩估计值有界,此结论是研究的基础;引理2It等距不等式表明次线性空间中随机积分二阶矩的运算性质,这与线性空间的It等距公式是不同的,在线性空间中等号恒成立,主要是因为次线性空间的次可加性(d)造成的;显然,It等距不等式是B-D-G不等式的特殊形式(p=2)。
关于更多G-期望、G-正态分布和G-布朗运动的研究内容请看Peng[1]的相关文章。为了更好研究G-布朗驱动下随机卷积积分的性质,下面将会介绍关于随机卷积积分的基础知识,具体请参考文献[11]和[12]。
无穷维空间比较复杂,其性质的研究需要借助算子来研究,算子A:D(A)→ H 是C0-半群(etA)的无穷维生成元,假设算子A生成一个正则半群,此外-A的预解集包含所有常数λ且Reλ> 0。我们可以定义算子-A的分数幂为(-A)γ,详见文献[13]。
设Hγ是(-A)γ的定义域,范数|·|γ定义为|x|γ=|(-A)γx|H,x∈Hγ,为了书写方便,记|·|H=|·|。
为了得到更实用的性质,下面介绍正则半群S(t-s):=e(t-s)A,0≤s 对于任意的γ> 0,存在常数Cγ> 0使得 |(-A)γS(t-s)|≤Cγ(t-s)-γ,0≤s (1) 若γ∈(0,1]且x∈Hγ=D(-A)γ,则 S(t-s)x-x≤Cγ(t-s)γ(-A)γx (2) 另外,假设y 是从[0,T]到Hγ的函数,定义‖y‖γ,p如下: 本小节结合无穷维空间传统布朗运动驱动的随机卷积积分和G-布朗运动驱动下随机卷积积分,在合适的条件下,利用因子公式分解法证明无穷维G-布朗运动驱动下随机卷积积分的Hölder连续性。因子分解法的具体内容和应用,详见参考文献[3]和[14]。 下面给出半群S(t-s)的抛物型条件: 随后,考虑 (3) 其中,对任意的β∈(0,1],ys是从[0,T]到Hβ的函数。 (4) 其中p>2无限大。 根据定义,可以将z(t)进行分解: =Z1+Z2。 先来证明第一部分,由(1)可得: (5) -s))ys]ds|,显然有Z2≤Z2,1+Z2,2,下面对于这两部分分别进行推导,关于Z2,1可以得到 (6) |(-A)γ(S(v-s)-S(u-s))y(s)| ≤|(S(v-s)-I)(-A)γS(u-s)y(s)| ≤Cλ(-A)γ+λ-βS(u-s)|y(s)|β 因此 (7) 根据(5),(6)和(7)式,得到(4)式成立。 本节将给出无穷维空间中G-布朗驱动的随机卷积积分的有界性。此外,基于参考文献[15]中希尔伯特空间下Sz.-Nagy意义的酉扩张的方法,给出弱极大值不等式。 下面的定理给出了随机卷积积分It的有界性。 证明由Hölder不等式和(3)式的关系,对任意的T≥0,有 根据定理8的证明和Y(s)∈L2m(0,T;H),若m>1 ,有 其中常数Cp>0。 对于任意t≥0,存在μ≥0使得压缩半群(etA)满足‖etA‖L(H)≤etμ,通过考虑压缩半群(e-tμetA)t≥0,很容易能够得到以下极大值不等式。 定理3设(etA)是H上的C0-半群,对任意的t≥0且存在μ≥0,满足‖etA‖L(H)≤etμ,则当p∈(0,+∞)时,存在常数0 无穷维空间中的随机卷积积分来自数学和金融学,其中较为有名的远期利率曲线就是Heath-Jarrow-Morton-Musiela方程的解[16]。随机卷积积分被作为重要的工具应用于随机偏微分方程中相关解的性质的研究,关于它的一些不等式,例如极大值不等式和指数扩张定理等,对随机方程的理论证明起到有力的推动作用。G-期望理论是概率论中一个方兴未艾的方向,目前国际上已经有越来越多的概率论统计学方面的学者开始专注这一领域的研究,而对于无穷维G-布朗运动的研究少之又少,对于其随机卷积积分性质的研究也是极少的。本文主要是在前人研究的基础上,在适当条件下,利用合适的方法对G-布朗运动及随机卷积积分的性质做出更多的推广和改进。本文通过传统的因子分解法得到抛物型假设下无穷维空间中G-布朗运动驱动下的随机卷积积分的Hölder连续性,随后利用Hölder不等式和简单的推导,证明出随机卷积积分是有界的,有界性质为卷积的研究奠定了基础。最后基于Sz.-Nagy定理的酉扩张方法得到G-布朗运动驱动下的随机卷积积分的弱极大值不等式,相关更强的结果以及指数扩张定理也值得继续关注。G-布朗运动驱动下的随机卷积性质是随机方程分析的基础和重要的工具,对偏微分方程粘性解的性质的研究具有实用价值,但是文章得到的最终结论还有待进一步深入推进,后续工作将会继续跟进。2 Hölder连续性
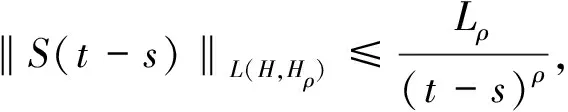
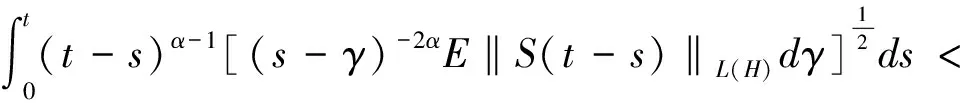
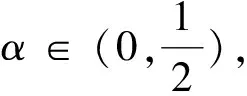
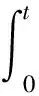
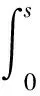
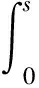
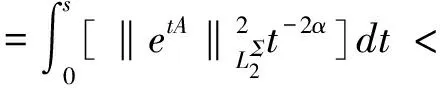
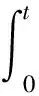
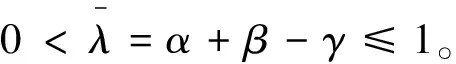
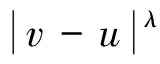
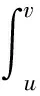
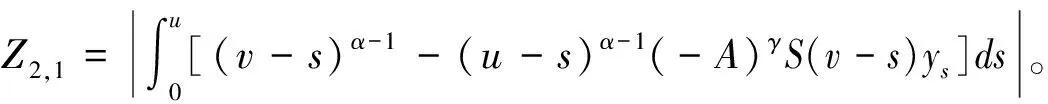
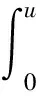
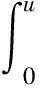
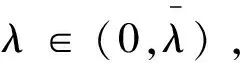
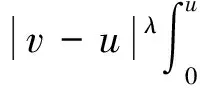
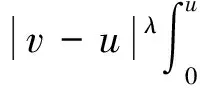
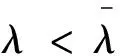
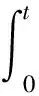
3 有界性和弱极大值不等式
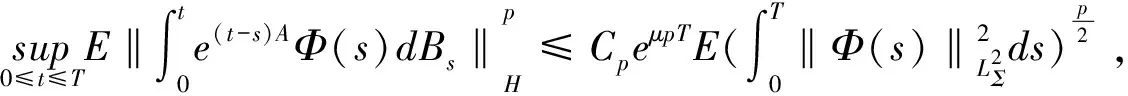
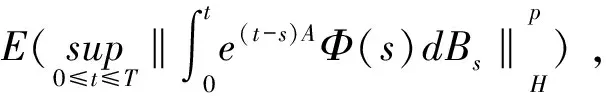
4 结 语
——2018年全国高考Ⅲ理科数学21题别解

