波浪滑翔机襟翼辅助推进控制系统设计

刘胜 王征

（哈尔滨工程大学，哈尔滨，150001）

波浪滑翔机前进的推力全部来源于波浪运动，海洋环境的变化使其推力随机变化，航行速度也难以人为控制[1]。波浪滑翔机水下牵引机所安装的水翼吸收波浪能被动翻转，为整个装置产生前进推力。这是设计研发的重点[2]，水翼的运动如图 1所示。水翼的摆动攻角对波浪滑翔器的推力转化、推进效率有直接的影响。而现有的波浪滑翔机水下牵引机安装的水翼均为单一控制面。在水下牵引机选择和设计时，通过调整弹簧结构参数、水翼最优限位角等，使潜体水翼运动效率达到均衡的状态[3]。然而该潜体水翼通常只能满足在指定的几个工况下达到最佳性能。在波浪滑翔机长时间运行条件下，波况状态随机，变化较大，现有设计难以达到最佳性能[4]。

图1 波浪滑翔机运动原理

为提高波浪滑翔机的控制性能和能量利用效率，本文提出了一种襟翼辅助推进的控制思想。通过为波浪滑翔机潜体水翼机构的主水翼后缘增加襟翼装置，将单一控制面变为两个独立运动的控制面，人为的控制后缘襟翼旋转角度，进而大幅度的改变主水翼等效攻角，使水翼产生的推力大小在一定范围内是可控的，目的是通过人为控制波浪滑翔机的推进力，从而改善其机动性能。

襟翼提高升力或加大力矩的思想被广泛应用于航空航天以及航海等领域[5]。目前，波浪滑翔机的水翼采用 NACA系列对称水翼，此类型水翼被应用于各种扑翼机构上。在船舶水翼舵的应用中，文献[6]提出的襟翼舵伺服控制系统，将舵和翼舵作为两个独立的控制面进行控制。通过舵/翼舵的联合控制，提高了舵的扶正能力，有效减少了船舶的艏摇运动。方亮[7]研究了舵角/翼舵角智能优化分配规则，提出“系统驱动能量最小”原则下舵角/翼舵角分配规则，并用遗传算法进行优化。孙志[8]利用卷积神经网络对舰船舵-翼舵联合控制中的故障进行预测，较传统方法显著的降低了故障误报率。

本文将襟翼有关思想引入到波浪滑翔机水下牵引机构中，在波浪滑翔机航行时需要跨越较大面流海区或者在海流区进行控位作业时，用于提供短时间的辅助推进，在小能耗的情况下改善波浪滑翔机的运动性能。仿真结果显示，该襟翼控制思想可有效提高波浪滑翔器航行速度。

1 波浪滑翔机动力学模型

上海交通大学吕元博[9]结合波浪滑翔机多体结构的特点，对波浪滑翔机的三个主要部分进行联合数学建模，并对波浪滑翔机整体的复杂运动情况进行计算求解。本文直接引用其模型并对潜体水翼模型进行改进，增加襟翼独立控制面，验证本文提出方法的优越性。

1.1 波浪滑翔机动力学模型

水面母船随波浪升沉过程的动力学控制方程为

水下滑翔体随波浪升沉过程的动力学控制方程为

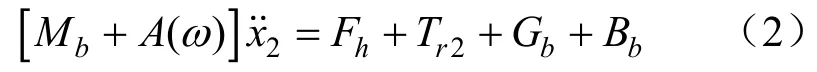
柔性缆计算模型：

以上变量参数取值均参考文献[9]。

1.2 具有主动偏转后缘襟翼能量的提取

1.2.1 振荡水翼参数的计算

传统振荡水翼通过起伏和俯仰运动从周围流场提取动能。可将运动形式分解为瞬时起伏运动h(t)和俯仰运动θ1：

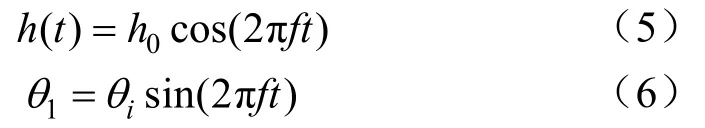
本研究中在振荡水翼添加一个后缘主动襟翼控制。定义襟翼偏转角为θ2，偏转幅度为θj，其运动形式描述为

振荡频率通常统一定义为

式中，U∞为来流速度，c为弦长。

瞬时俯仰系数力CY(t)与俯仰力矩系数CM(t)分别为

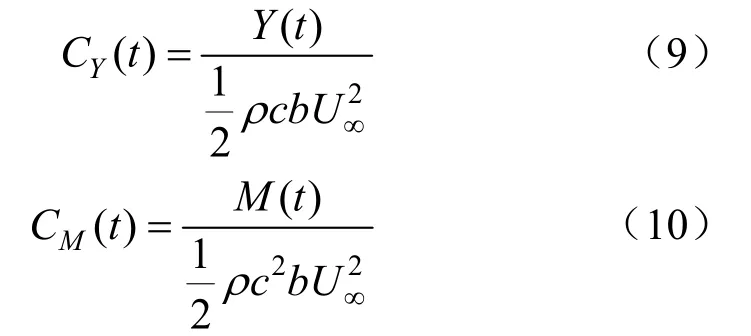
瞬时起伏力CPY(t)与俯仰力矩的功率系数CPM(t)分别为

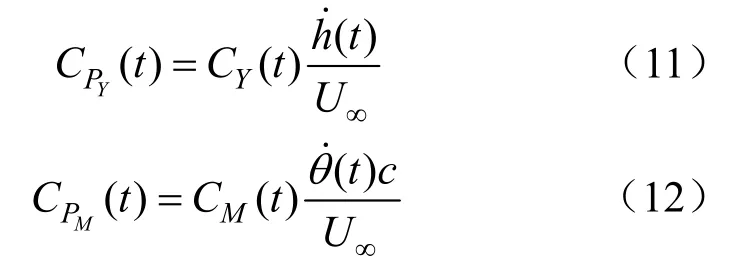
总功率输出系数与效率表示为

式中，d为水翼扫掠的最大垂直距离。

1.2.2 振荡水翼数值模拟

计算流体动力学（Computational Fluid Dynamics，CFD）工作基于fluent求解，在相同的条件下模拟比对传统水翼与新型襟翼水翼之间的性能。本研究中采用 NACA0018翼型，在水翼后缘 0.2c处改为尾缘襟翼结构，计算域网格如图 2所示。在俯仰中心到入口边界的距离为 35c，到出口边界的距离为40c，水翼主体周围采用O型网格，后缘襟翼采用 C型网格。用户定义函数（User-Defined-Function，UDF）用于实现箔片的振荡运动和后缘襟翼的偏转运动。

图2 具有边界条件的计算域

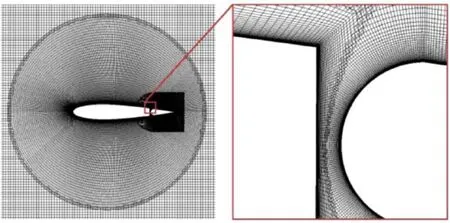
图3 水翼振荡模型网格细节

本文主要研究为襟翼的控制系统设计，重点对襟翼控制器的设计，因此水动力数值模拟仅验证襟翼水翼相较于传统水翼的优越性。新型襟翼水翼水动力效率作以下简略分析。

设定模拟条件雷诺数Re=500 000，主水翼俯仰轴Xa=1/3c，俯仰幅度θ0=75°，升沉幅度 1 m。图 4（a）显示了水翼在一个周期内的平均能量提取效率。为了评估后缘襟翼的增强效果，研究中计算了效率差 Δη，该效率差等于后缘襟翼水翼的效率减去相应频率下传统水翼的效率。图 4（b）显示了两种水翼之间效率差值的等值线。

图4（a） 新型襟翼水翼的能量提取效率

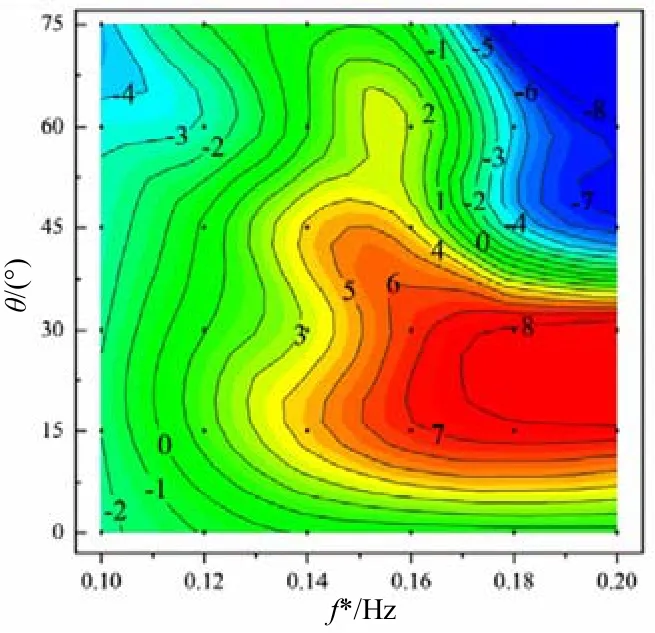
图4（b） 两种水翼在各种振荡频率和偏转幅度下的效率差

图 4（b）表明，后缘襟翼大大提高了摆动水翼能量的提取效率。当振荡频率f*接近0.2时，与相对较低的频率相比，后缘襟翼转动的影响更为明显。当偏转幅度θ位于 15°～30°范围内，能量提取性能在宽频率范围内得到增强。

1.3 系统驱动能量建模

本文设计的襟翼辅助推进控制系统采取和主水翼同时运动的控制策略，目的是使水翼整体在较短的时间内运动到最优等效攻角。

水翼整体转动角度：

刚性襟翼控制规律表示为

式中，J为襟翼的转动惯量。

将式（16）转化为用于可计算时间步长的式（17），计算控制过程中每时间步襟翼的运动角度。

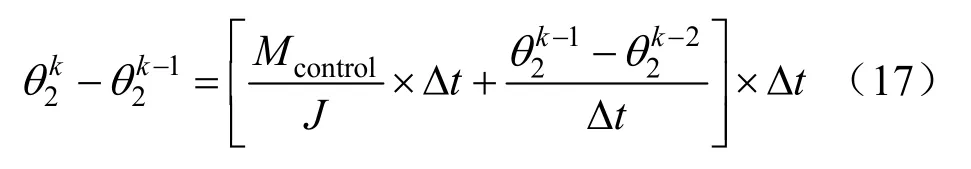
2 襟翼辅助推进控制系统设计

本文的控制设计要求为滑翔机的航速生成一个稳定的控制器，该控制器由襟翼控制。系统只有一个输出（滑翔机的航速）和一个输入（襟翼角），但响应也取决于滑翔机襟翼摆动速率与攻角，而襟翼摆动速率与攻角取决于海况。对于这种单输入单输出（Single-Input Single-Output，SISO）系统，PID设计方法有一个简单且定义明确的控制结构。本文设计一个用于滑翔机襟翼摆动速率控制的内部控制器和摆动角度控制的外部控制器。控制方案如图5所示。

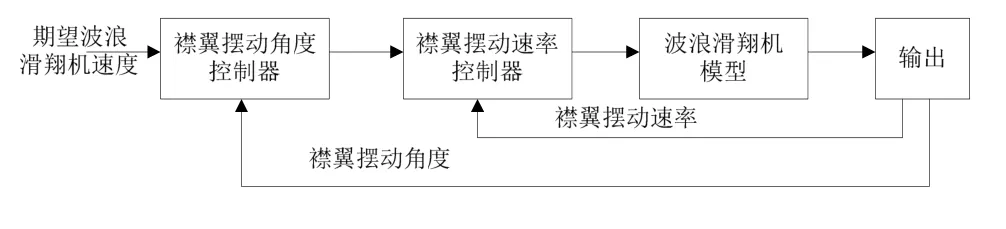
图5 控制系统总体方案

图 5中，对于给定的期望波浪滑翔机速度设定点，滑翔机襟翼摆动角度控制器根据模型输出的反馈，确定所需转角并输出给滑翔机襟翼摆动速率控制器；该角度输入滑翔机摆角速度控制器，以控制襟翼转动时间，然后输入模型。根据波浪滑翔机运动特点，襟翼模糊 PID串联控制系统的结构图如图6所示。

图6 控制系统设计方案

2.1 模糊PID串联控制算法

不同海况下，波浪滑翔器水翼转动具体角度规律未知，且目前针对不同海况水面船的船速和与之对应的潜体水翼的转动角度研究不足，因此本文针对这种不确定关系采用模糊控制算法。同时为了提高襟翼控制系统性能，提出“粗调+精调”的层次递进控制思想。即在襟翼摆动角度控制的外部控制器使用模糊控制算法，内部控制器襟翼摆动速率采用 PID高精度控制。为此，设计了模糊-PID 串联控制器，以实现智能控制策略。通过设计模糊控制器，使其在复杂随机海况下，模糊控制器输入为水面船期望速率与实际速率误差，输出潜体水翼的襟翼角度控制信号，把输出角度给 PID 控制；设计 PID 控制器时，对襟翼摆动的速率进行精确控制，并采用线性模型设计降低建模难度。从而实现了襟翼角度的“粗略”控制与襟翼转动速率的“精确”控制。

两种控制算法的串联，是根据各自算法作用的控制输出量特点体现出来的，它们实时共同起控制作用，不同于简单的阈值切换控制。实质上，模糊-PID串联控制器相当于一个互补型的智能控制器，使控制系统的鲁棒性和控制精度都得到了改善。

2.2 模糊控制器设计

模糊推理机是模糊控制器的核心部件，它把水面船航速的e和分别变换成两个模糊输入变量E和EC，然后构成模糊控制集U。本文设计的系统中，输入为航速的偏差e和，输出为襟翼的角度控制集U。分别对应其量化因子ke、和比例因子ku。考虑到ke(t)、、ku(t)的动态修正因子对于控制系统的影响来说是非线性的，不同阶段影响大小不同，并且相互影响制约。因此根据实际情况，采用粒子群算法对模糊-PID控制进行优化，以此来实现控制系统的最优化问题。

粒子群计算方法为

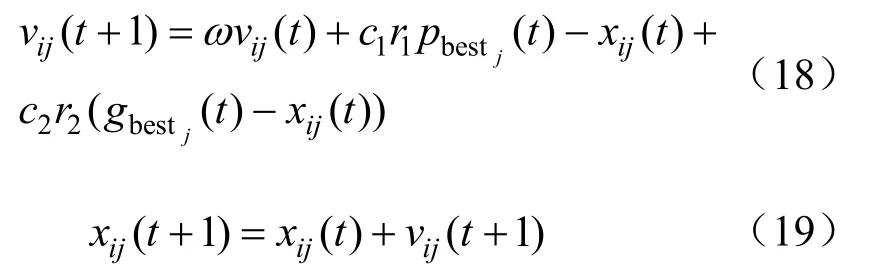
式中，ω为惯性权值，vij(t)是粒子i在进化到t代时的第j维速度分量，xij(t)是粒子i在进化到t代时的第j维位置，pbestij(t)是粒子i在进化到t代时的第j维个体最优位置pbesti(t)分量，pbestj(t)是进化到t代时整个粒子群的最优位置pbest的第j维分量，c1、c2为加速因子，r1、r2为[0,1]内随机数。

对于襟翼辅助推进控制系统，量化因子ke(t)、、ku(t)的值影响控制系统的动态性能。较大的ke(t)会使系统超调过大；较大的减小超调量，但会减慢系统的响应速度；输出比例因子ku(t)选择过小使得系统的动态响应变慢，选择过大会使得系统出现振荡。为了获取最优的量化因子和输出比例因子，以积分性能指标（Integral of Time and Absolute Error，ITAE）作为寻优目标函数。ITAE公式表示为

粒子群优化算法如下：

（1）初始化粒子种群。设定空间维数d=3，初始粒子N=30个，更新迭代次数t=50次，惯性因子ω∈[0.4,0.9]，并在范围上线性变化，学习因子c1、c2∈[0,3]。

（2）进行适应度计算。将每个粒子的位置作为待优化因子的参数值，通过 ITAE积分性能指标，计算各个粒子的适应值，更新pbest和gbest的值。

（3） 调整当前粒子的速度和位置。根据式（18）、（19）计算当前的位置和速度。

（4）检查算法终止。若迭代次数达到上限或者得到最优适应值，程序终止；否则，转至第（2）步继续寻优。模糊规则表如表1所示。

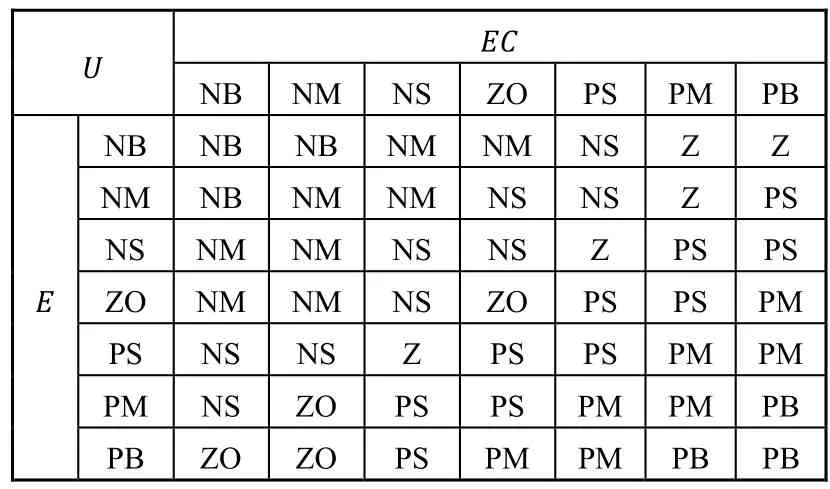
表1 模糊规则集

当波浪滑翔器处于 1级海况时，潜体水翼转动幅度较小，则襟翼做大幅转动角度，使水翼整体转角达到理想角度；当波浪滑翔器处于 6级以上海况，潜体水翼处于极限运动状态，且转动速率快、幅度大，此时控制器输出指令，使水翼整体转角减小，船速降低，以保持船体稳定性。

在隶属度函数选择时，采用模糊集合的宽度越窄，则隶属函数的偏差灵敏度、精度越高；采用模糊集合的宽度越宽，则隶属函数的偏差分辨率较低，偏差控制灵敏度也相应较低，控制特性较平缓，稳定性也较好。因此，一般在误差较大时采用低分辨率的隶属函数，误差较小时，宜采用高分辨率的隶属函数。高斯性隶属函数的平滑性较好，概念较精确，所以本文中的模糊隶属函数均采用高斯MF型函数。

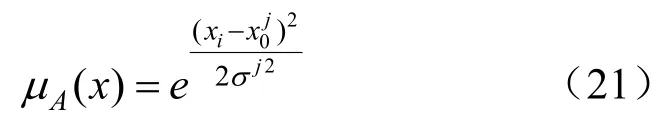
2.3 PID控制器设计

（1）本设计中襟翼最大转动角度θ=45°，转动周期T=3 s，电机转动惯量J=0.015 kg·m2，电机转矩常数KT=0.4851 N·m/A，电机阻尼系数B=0.267。将襟翼的运动看成等效正弦运动，设其运动频率为ω，即

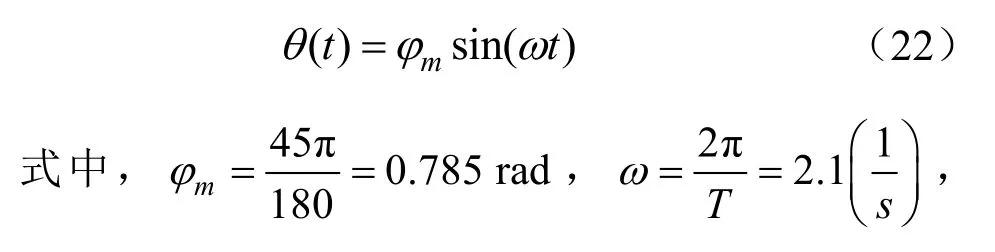
3 系统仿真

在波浪滑翔机实际行进过程中，潜体水翼可能随海况的不同而运动方式不同，3种翼板运动方式如下：

运动方式 1：波浪滑翔机潜体水翼随波浪运动做周期性正弦变化，对应1～2级海况。

运动方式 2：波浪滑翔机潜体水翼在运动至平衡位置附近时，以固定攻角做纯升沉运动，对应 3级海况。

运动方式 3：波浪滑翔机潜体水翼运动方式为阶跃信号，在水流的作用下直接变成最大角度滑翔，对应6级以上海况。

对以上3种翼板运动方式编写函数带入本文所建立的动力学模型进行仿真。输入 3级海况(H=0.8 m，T=4 s)下进行仿真验证 3种翼板运动方式对波浪滑翔器前进速度的影响。图7为不同翼板运动方式下波浪滑翔器前向速度随时间的运动关系，图 8为对应的水面船前向位移。蓝线表示翼板正弦运动下的前向速度，红线表示方式2的前向速度，黄线表示方式3下的前向速度。

图7 三种翼板运动方式下前进速度对比

图8 三种翼板运动方式下水面船水平位移曲线

从图7中可以看出，波浪滑翔器能够获得最佳前向速度是翼板能够以脉冲信号形式响应的运动方式。3种不同的翼板运动方式运动速率的不同为本文襟翼辅助推进提供了控制可能性。本文设计的波浪滑翔机襟翼辅助控制系统，通过改变潜体水翼整体的等效攻角，并控制其运动时间，进而控制翼板在不同等级海况的运动方式，实现人为控制波浪滑翔机的航速。

由图 7所示，水翼的运动方式对波浪滑翔器的航速有重要的影响。在本文所设计的海况下，水翼正弦运动时波浪滑翔机的前向速度最低，水翼呈阶跃形式运动时波浪滑翔机的速度最高，以二者结合的方式波浪滑翔器的运动速度虽然整体上不如阶跃信号，但是相差并不是很大。分析水翼正弦运动与阶跃运动速度相差较大的原因可能是水翼在波峰或者波谷时，翻转需要一定的时间，时间越短，以较大攻角行进的时间越长，产生较大推力的时间更久，利于波浪滑翔机的前进。因此控制襟翼转动时，在不影响稳定性的前提下，应尽可能缩短时间。

图 8为 3种不同的翼板运动方式下水面船在50 s内的位移曲线。由图可以看出，在每个周期内，水面船的前向运动曲线都有一定范围内的波动，并不是匀速运动，与图 7显示的速度相印证，从一定程度上验证了模型的准确性。

对所建立的模型设计了如图9所示的模糊-PID串联控制器时域仿真程序，绿色模块分别为模糊控制与 PID控制，蓝色模块为仿真海况输入，红色模块为波浪滑翔机模型。程序针对控制器对正弦、阶跃信号的跟踪控制过程的超调、上升时间、稳态误差、整定时间等指标进行比较分析。

图9 模糊-PID串联控制器时域仿真程序

图10～11显示了在文中3级海况条件下针对不同期望翼板运动方式控制器的控制性能，蓝线代表期望输出，红线代表实际输出。

图10 在海流干扰下控制器对正弦信号的跟踪效果

图11 在海流干扰下控制器对阶跃信号的跟踪效果

图 10中，角度变化相对平缓，没有明显的超调，并且响应也很迅速。图 11显示，在阶跃信号变化的瞬间，都会产生一定的超调，但都迅速稳定下来。表 2给出了不同海况下传统水翼与襟翼控制水翼下水面船的船速仿真结果。从表 3中可知，相较于模糊-PID控制，基于粒子群算法优化的模糊-PID控制作用下速度响应的稳态误差明显减小，系统的调节时间大大缩短。

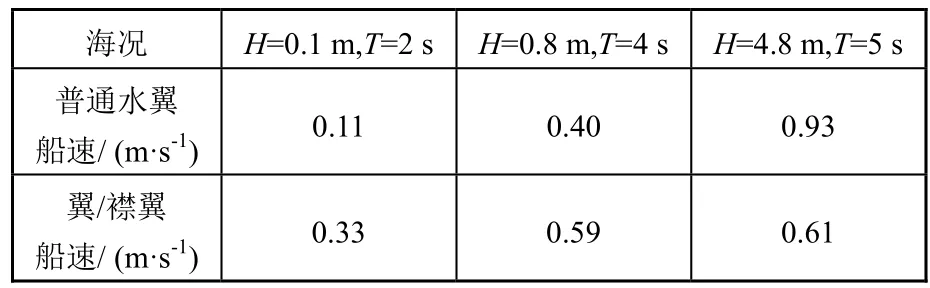
表2 不同海况下水面船船速仿真结果

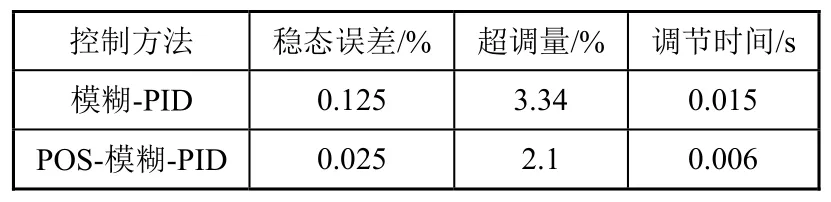
表3 两种控制作用下速度响应的性能参数

综上所述，本文提出的波浪滑翔机襟翼辅助推进控制方法，可有效提高波浪滑翔机速率，且设计的控制系统具有良好的抗干扰和自适应性能。

4 总结

襟翼辅助推进系统并不是实时工作，而是在特定情况下（如需进行增加动力或者控位作业），通过控制器发出指令，执行相关动作，在小能耗的条件下，改善波浪滑翔机弱机动性。本研究通过建立波浪滑翔机动力学模型，并带入 POS-模糊-PID串联控制器时域仿真程序，得出以下结论：

（1）利用襟翼来增加波浪滑翔机潜体水翼等效攻角有利于提高波浪滑翔机的推进力。

（2）襟翼辅助推进系统可以改变翼板运动方式，有利于提升波浪滑翔机的机动性。

（3）本文设计的 POS-模糊-PID控制器采用“粗调+精调”的思想，不仅具有良好的稳定性和动态效果，而且结构简单，易于工程实现。