可靠声路径匹配波束强度处理目标深度估计的克拉美罗界研究
钱富 朱方伟 王嘉
(1.海装驻杭州地区军事代表室,杭州,310023;2.第七一五研究所,杭州,310023)
近年来,实验观测到临界深度下的背景噪声低于临界深度的背景噪声5~20 dB。经由可靠声路径传播声信号的传播损失小于同等距离浅海传播损失 10~20 dB[1-3]。这些优势使得布放在临界深度下的垂直阵可基于可靠声路径(直达路径与海面反射路径结合)用于深海近海面声源的检测和定位[4-5]。考虑到深海可靠声路径模式下,目标距离与信号到达俯仰角的对应关系,因此可靠声路径目标距离的估计是容易的。国内外学者近年的研究重点集中在利用可靠声路径声场干涉特性的目标测深方法和技术,取得了大量的研究成果[6-9]。利用直达路径和海面反射路径的叠加(劳埃德镜干涉)引起的距离-深度平面内的干涉条纹,解释了对于一个窄带信号,其能量作为距离的函数受到声源深度的调制变化。这种调制变化可用于声源深度的估计,广义傅里叶变换与过零检测的方法被用于目标深度的估计。
Yang等人[10]解释了声强作为频率的函数受声源深度的调制,并利用频谱的周期性估计声源的深度。Duan等人[11]使用扩展的卡曼滤波,利用干涉结构估计声源深度,并且利用单水听器多途结构实现了声源的定位。Zheng等人[12]将非相干匹配波束处理用于估计声源深度,该方法匹配数据波束峰值随时间变化并假定声源深度下拷贝波束峰值随时间变化,拷贝波束与数据波束匹配最佳的位置即为估计的声源深度。与傅里叶变换法相比,在相同距离与角度跨度的情况下,该方法可获得更高的声源深度估计精度,并且更适用于估计近海面声源的深度。最新的研究成果中,Zhou和 Zheng等人[13]在窄带匹配波束强度处理的基础上,提出了通过峰值波束强度频率干涉结构匹配的深度估计方法,用于实时或者半实时的目标深度估计与辨识。
深海可靠声路径被动目标深度估计是利用可靠声路径声场时空特性进行目标深度信息拾取,是深海目标探测中的关键问题。克拉美罗下界(Cramer-Rao Bound,CRB)描述了参数无偏估计方差的最小值,能够反映参数估计算法的理论最佳性能,在参数估计理论中扮演着重要的角色。本文研究在Zhou和Zheng等人研究的基础上,理论推导了宽带匹配波束强度处理的克拉美罗界,基于仿真数据分析了信噪比、处理带宽等因素对目标深度估计性能的影响。
1 宽带匹配波束强度处理方法
如图1(a)所示,对于布放在临界深度以下的垂直接收阵,中距离的声源辐射噪声可经由可靠声路径到达深水接收器,到达接收器的声信号为直达声和海面反射声的叠加,不包含海底反射声(由于大掠射角对应高海底反射损失,因此可以忽略海底反射)。垂直阵布放在临界深度以下,声源与垂直阵距离为R,以深度zs运动。声源辐射噪声为宽带信号100~300 Hz,且在有限快拍下是随机的,如图1(b)所示。图中,直线表示平均频谱幅度,波浪线代表用有限数量的快拍估计的频谱。

图1(a) 声源和接收器位置
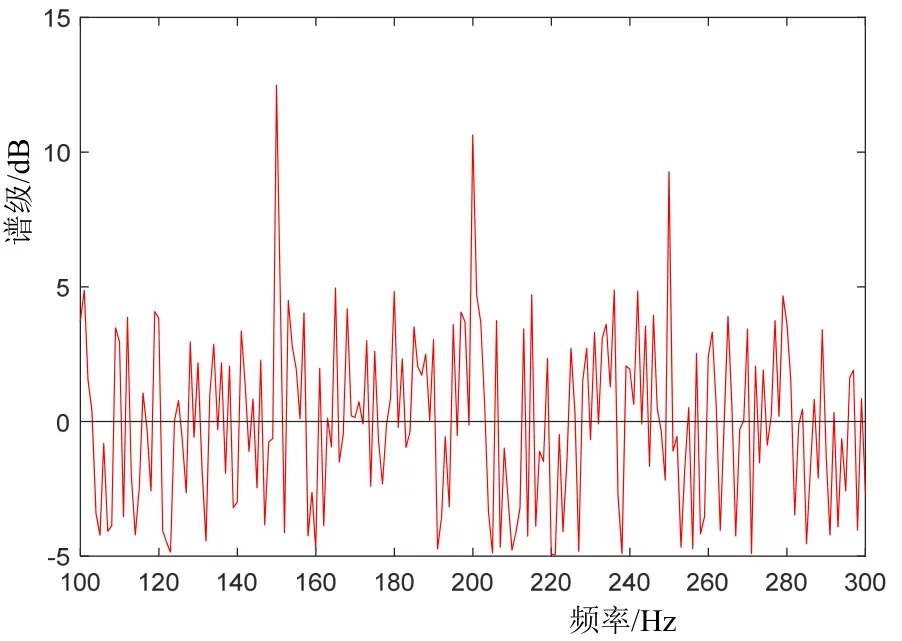
图1(b) 未校准的声源辐射噪声频谱示例
在海水等声速及忽略声线折射的假设下,垂直阵接收窄带信号的声压场可由劳埃得镜预测得到。深度zj处水听器接收距离R、深度zs处的声源的声场可表示为
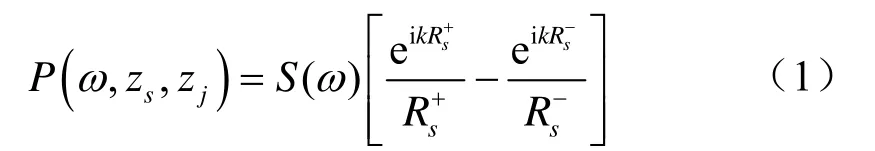

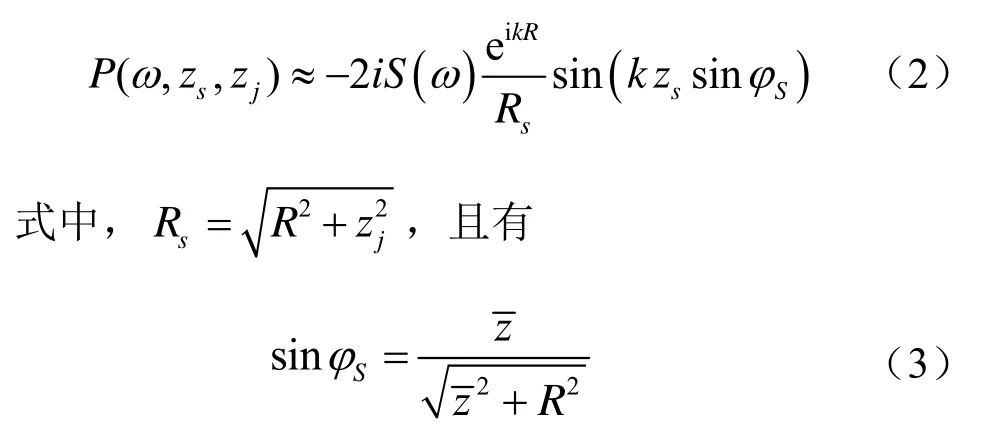
式中,为垂直阵中心位置所在深度。给定一个N元垂直阵的接收信号,可以应用如下的常规波束形成:
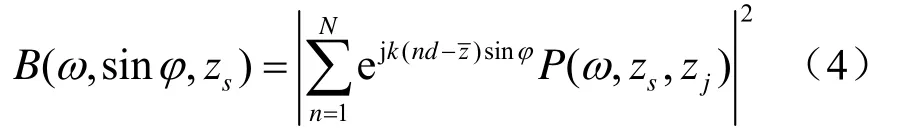
当sinφ= sinφS时,波束能量达到峰值:
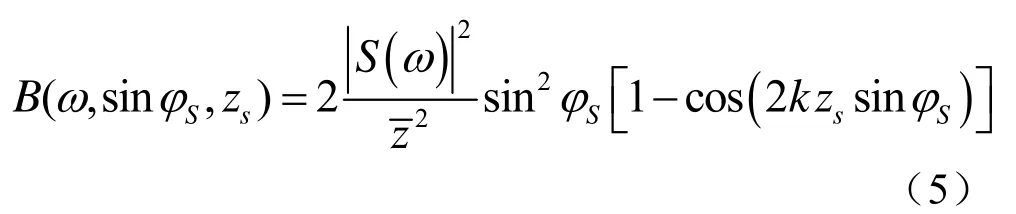
仿真海深5000 m情况下,基于Kraken计算典型Munk水文环境下的深海声传播损失分布,如图2所示。可以看出,距离25 km范围内,近海底为直达声区,其传播损失小于近海面处的传播损失,因此可以利用直达声区传播损失小的优势,用布放在近海底的大孔径垂直阵列进行近海面声源目标的探测。基于宽带波束形成提取声信号到达角随距离的变化如图3所示,可见可靠声路径模式下,目标距离与信号到达俯仰角的对应关系。

图2 深海声传播损失分布(频率100 Hz)

图3 声源深度50 m、频率100 Hz的传播损失
至此,可将B(ω,s inφS,zs)作为广义处理的参量,定义观测信号模型。假设对于所关注的频段,可以获得L个独立的数据样本,接收信号可表示为
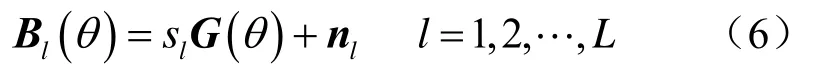
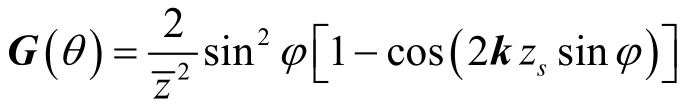
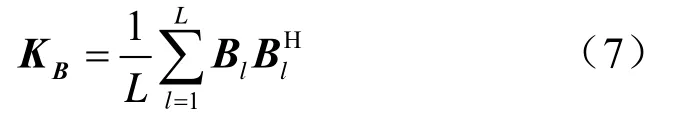
2 宽带匹配波束强度处理CRB的推导过程
CRB描述了参数无偏估计方差的最小值,在参数估计理论中具有重要的意义,即给定了对于任意的无偏估计量,它的方差肯定大于或等于一个给定的值。如果存在一个估计量,对于每一个θ,它的方差等于CRB,那么这个估计量一定是最小方差无偏估计量。在实际中,最小方差无偏估计量并不是始终存在的,因此 CRB可以作为无偏估计量的性能下限,并提醒我们不能求得小于 CRB的无偏估计量。在第1节宽带处理框架下,推导匹配波束强度处理的CRB。
考虑一组未知但非随机的参数θ(本研究中为声源目标深度),T(r)代表观测数据的统计量,∑代表均方误差矩阵,则有
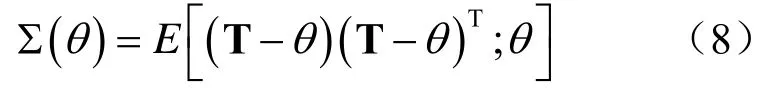
该矩阵的下限为

对于CRB,其中Fisher信息矩阵J(θ)与对数似然函数的关系如下:
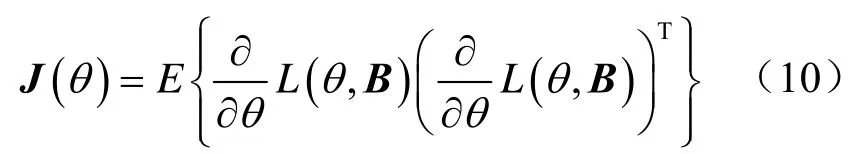
对数似然函数与似然函数为
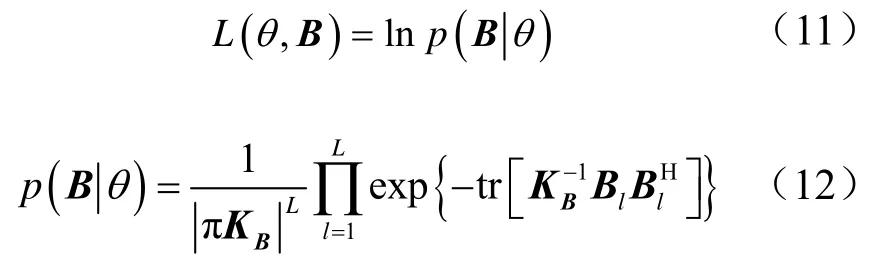
若仅考虑目标深度的估计,依照文献[14]的推导过程,可以获得接收信号模型为式(6)、噪声模型为白噪声模型的Fisher信息矩阵:

式中,波束强度函数对待估计参数的偏导表示如下:
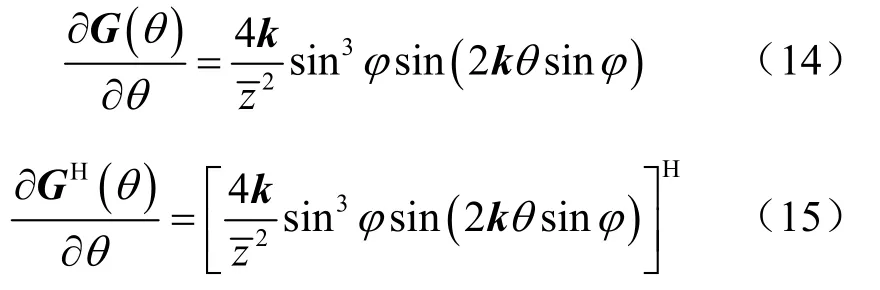
3 仿真分析
3.1 深度估计标准差下界与信噪比的关系
仿真设定处理频段100~300 Hz,目标深度50 m,目标距离分别设置5、15 km,并依据设定的目标距离信号到达俯仰角的对应关系,估计信号到达俯仰角的正弦,进而计算 CRB表达式中的各项参数。设定信噪比由-20 dB变化至10 dB、理论计算的处理频段100~300 Hz情况下,深度估计标准差下界随信噪比的变化如图4所示。可以看出,信噪比对深度估计性能的影响显著,当信噪比由-20 dB变化至10 dB时,深度估计标准差下界减小了两个数量级。此外值得注意的是,目标距离15 km时,深度估计标准差的下界始终高于目标距离5 km情况下的深度估计标准差下界,这说明了深度估计的性能与目标距离是有关的。
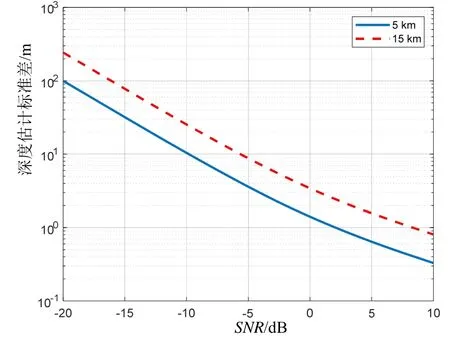
图4 深度估计标准差下界随信噪比的变化
3.2 深度估计标准差下界与目标距离和深度的关系
为了研究目标空间位置对深度估计性能的影响,设定信噪比5 dB,处理频段100~300 Hz,取目标深度在1~300 m变化,间隔1 m,目标距离在1~25 km范围内变化,间隔0.1 km,仿真深度估计标准差下界随目标空间位置的分布如图5所示。可以看出,目标距离越远,深度估计标准差下界越大。原因是目标距离越远,声信号到达俯仰角(正弦)越小,由式(13)可知Fisher信息矩阵与声信号到达俯仰角(正弦)成正相关,故深度估计标准差下界与声信号到达俯仰角(正弦)成反相关,即与目标距离变化成正相关。物理上,原因是声信号到达俯仰角(正弦)越小,波束强度的宽带变化起伏变缓,周期数变少,导致匹配频域干涉结构的深度估计性能变差。
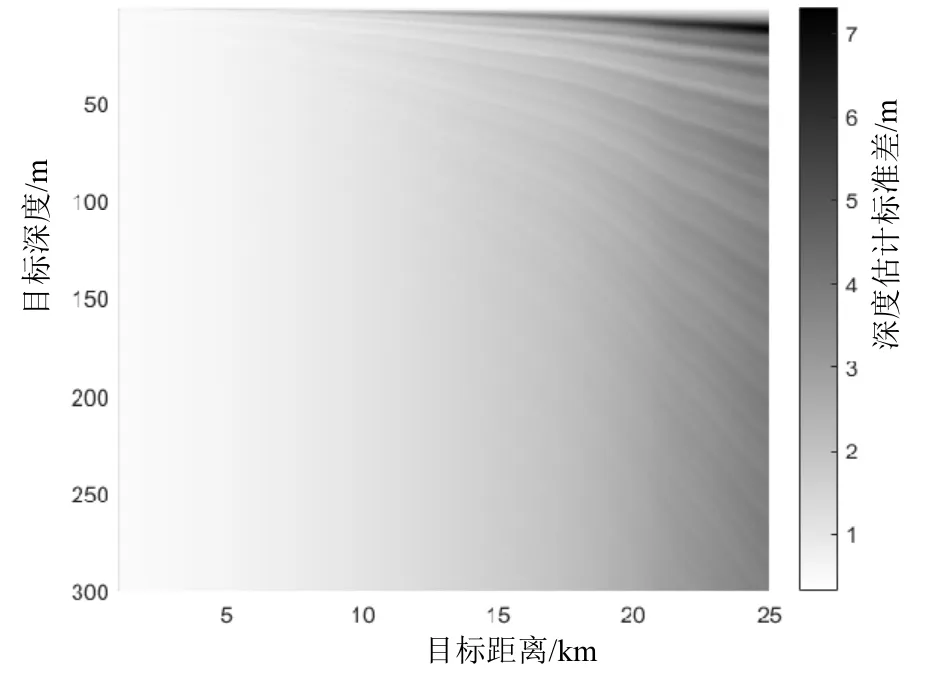
图5 深度估计标准差下界随目标空间位置的分布
图6给出了图4中不同距离切片情况下,深度估计标准差下界随目标深度的变化。可以看出,目标深度小于10 m时,深度估计标准差下界存在一个峰值,当目标深度大于50 m时,近距离处目标的深度估计标准差下界几乎不变,远距离处目标的深度估计标准差下界存在一定的起伏变化。
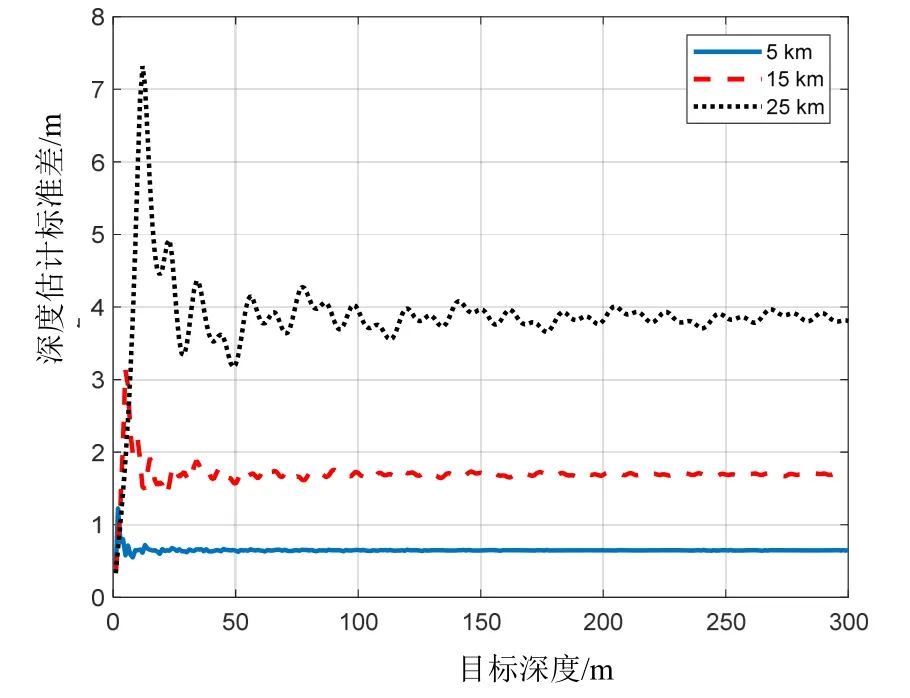
图6 深度估计标准差下界随目标深度的变化
3.3 深度估计标准差下界与处理带宽的关系
设定信噪比5 dB,处理频段下限频率100 Hz,处理频段上限频率由200 Hz变化至500 Hz,即处理带宽由100 Hz变化至400 Hz,仿真目标深度50 m,目标距离5、15、25 km情况下的深度估计标准差下界随处理带宽的变化如图7所示。可以看出,随着处理带宽的增加,深度估计标准差下界逐渐减小,深度估计性能提升。

图7 深度估计标准差下界随处理带宽的变化
3.4 深度估计标准差下界与俯仰角估计误差的关系
值得注意的是,基于垂直阵的可靠声路径目标测深是通过分步处理实现的,即先基于垂直阵波束形成测量信号到达俯仰角的正弦,随后基于测量俯仰角的正弦构建拷贝场的宽带波束强度进行匹配波束强度处理。显然俯仰角测量的精度影响深度估计的性能。
已知垂直线列阵的俯仰角-3 dB波束宽度为


仿真目标深度50 m,目标距离5、15、25 km情况下,深度估计标准差下界随俯仰角标准差的变化如图8所示。显然,俯仰角估计标准差越大(信噪比越低),深度估计标准差下界越大,深度估计性能越差。

图8 深度估计标准差下界随俯仰角估计标准差的变化
4 结论
本文针对深海可靠声路径宽带匹配波束强度处理目标深度估计性能下限分析的问题,理论推导了宽带匹配波束强度处理的克拉美罗界,基于仿真研究分析了信噪比、目标位置、处理带宽、俯仰角误差等因素与深度估计克拉美罗界的关系,得到以下结论:
(1)深度估计克拉美罗界随信噪比的增加而减小,即信噪比越高,深度估计性能越好。
(2)深度估计克拉美罗界随目标距离的增加而增大,即目标距离越远,深度估计性能越差。
(3)深度估计克拉美罗界随处理带宽的增加而减小,即处理带宽越大,深度估计性能越好。
(4)深度估计克拉美罗界随俯仰角标准差的增加而增大,即俯仰角标准差越大(俯仰角估计性能越差),深度估计性能越差。

