空间各向同性均匀噪声场中的子阵输出噪声相关性*

雷志雄，陈 鹏

(1.中国西南电子技术研究所，成都 610036；2.长安大学 信息工程学院，西安 710064)

0 引 言

空间各向同性均匀噪声场是信号处理领域中常用的一种噪声场，它假设相互独立的噪声从各个方向以等概率入射并叠加在传感器所在位置处[1-2]。在空间各向同性均匀噪声场中，当波束形成器指向平面波信号入射方向，阵列的指向性指数就等于阵增益，指向性指数(Directivity Index，DI)可以作为阵增益的估计[3]。由此可见，空间各向同性均匀噪声场模型可用于设计电磁学、声学阵列[4-7]，并且可以分析阵列的最优性能、优化阵列波束以及评估目标方位估计性能等[8]。

为了得到更好的阵处理结果，通常采用增加阵元数、扩大孔径以及采用超指向性或超增益波束形成方法，如最小方差无失真波束形成(Minimum Variance Distortionless Response,MVDR)、特征波束分解与综合方法等来提高阵增益和方位分辨力。在设计超指向性或超增益波束形成器时[3,9-11]，往往需要得到阵列的噪声相关系数矩阵，对于空间各向同性均匀噪声场中的无指向性阵元，其接收的环境噪声谱密度分布和方向无关，而阵元间的噪声相关系数为波数-距离的sinc函数[12]。

当阵元间距等于接收信号频率的半波长时，阵元间噪声相关系数为0，MVDR方法退化为常规波束形成方法(Conventional Beamforming,CBF)[13]。阵元间噪声相关系数不为0时，通过超指向性方法对接收的空间噪声进行“预白化滤波”，使得加权后的各阵元接收的空间噪声解除相关性，从而最大化阵增益[14]。

而上述这些方法存在一些弊端，如大孔径阵列随着阵元数的增加直接处理较难，超增益波束形成方法需要进行复杂求逆运算[15-16]且计算复杂度随阵元数增加而急剧增大等。为了克服上述问题，可以对接收信号进行子阵处理[17]。子阵处理利用不同的子阵划分方法，按照一定的准则将阵列划分成若干个小的子阵，并对子阵输出进行综合处理，可以有效降低计算复杂度，提升稳健性[18-19]。在子阵处理中，子阵可以等效为在其中心位置的一个指向性阵元，对于空间各向同性均匀噪声场中的指向性阵元，输出噪声的谱密度随方位变化。在实际应用中，无指向性阵元在高频范围中由于阵元位置误差等影响，输出噪声也表现出具有方向性[11]。与无指向性阵元不同的是，除了阵元间距，阵元间噪声相关系数还和指向性阵元的波束指向性有关，噪声相关性如果再用简单的波数-距离的sinc函数来描述，会导致噪声互相关矩阵的估计存在误差，造成波束形成和方位估计性能急剧下降等问题。

针对指向性阵元的噪声相关系数问题，Elko等人[4]提出了在各向同性均匀噪声场中的指向性阵元间噪声相关系数计算方法，并利用差分传声器阵列的空间波束响应可表示为cosnφ多项式的性质，得到了阵列输出噪声相关系数的解析形式[8]。但该方法对于任意指向性的直线阵列，难以得到输出噪声相关系数的解析解。

本文首先给出了任意指向性的共线线列子阵在空间各向同性均匀噪声场中噪声相关系数的解析解，得到了子阵常规波束形成的输出噪声相关性的一般形式，从而可以精确对线列子阵间的噪声协方差矩阵进行建模。在理论推导的基础上，利用数值仿真进行了验证，并讨论了子阵间噪声系数随子阵间距变化的趋势与子阵波束指向角、阵元数等子阵参数的关系。

1 噪声相关性理论模型

1.1 空间任意子阵输出噪声相关性

考虑一个阵列包含两个任意子阵，如图1所示，两个子阵分别包含M个无指向性阵元。

图1 任意子阵结构及坐标表示

两个子阵的阵元位置分别为

pi,m=[xi,m,yi,m,zi,m]T。

(1)

式中：m为子阵中的阵元编号,m=1,2,…,M;i为子阵编号,i=1,2。假设信号沿垂直俯仰角θ和水平方位角φ入射，则信号方向矢量为

v(θ,φ)=-[sinθcosφ,sinθsinφ,cosθ]T。

(2)

则子阵i的接收向量可表示为

ai(θ,φ)e-jkvT(pi,1-p1,1)x(f)。

(3)

式中：x(f)为子阵1的1号阵元接收的频域快拍；ai(θ,φ)表示子阵i接收某一角度信号的导向矢量；j为虚数单位；k=ω/c为波数，ω为角频率，ω=2πf，c为信号在介质中的传播速度；[·]T为转置。

对各个子阵分别进行波束形成后，子阵的加权向量wi可表示为

(4)

可得到子阵的频域输出

(5)

进而可以得到子阵的输出功率谱密度

(6)

式中：Sx(f)=x(f)xH(f)为子阵1的第1号阵元接收向量的功率谱密度。

根据定义，子阵1和子阵2输出的互功率谱密度可以写为

(7)

对于任意一个噪声场，阵元接收的空间噪声可以看作各个方向的独立噪声从远场入射到阵元的噪声叠加，相关系数由下式计算：

(8)

∮ASy1y2(f)dA=

r2sinθdθdφ。

(9)

波束输出的功率谱为

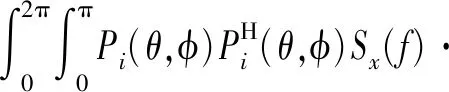
r2sinθdθdφ。

(10)

1.2 共线子阵的噪声相关系数

如图2所示，若将两个线列子阵都放置在坐标系z轴上，此时两个子阵是共线的。令zi,m表示第i个子阵的第m个阵元在z轴上的位置，将子阵1的第1号阵元置于坐标原点，即z1,1=0，此时到达各阵元的信号时间差和子阵的波束响应只随信号的到达角变化。

图2 共线线列子阵结构

将式(9)和式(10)代入式(8)，化简得到在三维各向同性均匀噪声场中，两个子阵首个阵元的坐标距离为子阵2的第1号阵元坐标z2,1，共线线列子阵输出噪声相关系数γy1y2可以用波束响应表示为[20]

(11)

式(11)计算子阵输出的噪声相关系数需要对各子阵的波束响应进行积分。Elko在2000年提出了差分传声器阵列间的噪声相关系数计算方法，其中N阶差分传声器阵列波束图可以写为cosn(θ)的多项式，进而可以得到阵列间噪声相关系数的解析解。而更为一般的波束形成方法需要先计算两个子阵的空间波束响应，再利用式(11)进行数值积分。因此，更为一般的子阵空间波束响应难以解析地得到，导致数值积分计算不仅存在误差，而且计算过程较为复杂。

在此，本文推导出三维各向同性均匀噪声场中，利用子阵波束形成器的权值向量计算子阵间噪声相关系数的解析方法。

根据定义，子阵的波束响应P1和P2可展开为

(12)

将式(12)代入式(9)，子阵输出互功率谱可写为

(13)

上式中的积分项可简化为

(14)

将式(14)代入式(13)中，得到子阵输出互功率谱的解析表示为

(15)

同理，可以得到两个子阵输出的功率谱分别为

(16)

将式(15)和式(16)代入式(8)，可得

(17)

由上式可知，空间各向同性均匀噪声场中，子阵输出的噪声相关系数可以用两个子阵的加权向量以及子阵的阵元坐标解析地计算，不仅避免了数值双重积分带来的误差，同时计算的复杂度大大降低。

对于两个阵型完全相同的子阵，且加权向量也完全相同时，简化式(17)可以得到

(18)

进一步，若两个子阵是完全相同的均匀线列阵，且子阵的阵元间距为d，则

(19)

当子阵内采用的是常规波束形成时，子阵的加权向量为wCBF=a(θ)/M，此时有

(20)

将式(20)代入式(19)，得到

(21)

2 仿真及结果分析

空间各向同性均匀噪声场可以看作来自空间中各个不同方向噪声源产生的远场平面波叠加，且这些噪声源互不相关且均是平稳的随机噪声[21]。本文仿真中，声速均取水下的典型声速1 500 m/s，均匀噪声场由均匀分布在半径远大于阵列孔径的空间球面上的360个独立噪声源构成，噪声源产生的复高斯随机序列的采样频率为8 000 Hz，序列长度为2 000点。对于每个阵元，将接收的所有方向的噪声叠加，再将噪声通过中心频率为1 kHz的带通滤波器(带通频率范围为980～1 020 Hz)，最终得到子阵中每个阵元的窄带噪声。

2.1 共线子阵的噪声相关性分析

由式(21)可知，子阵噪声相关性受子阵阵元数、子阵的波束指向角以及子阵中心间距三个变量影响。假设子阵为均匀线列阵，阵元间距为0.75 m，且两个子阵阵元数以及加权系数都相同，采用常规波束形成。在子阵共线场景下，分别对子阵阵元数、子阵波束指向角和子阵中心间距对噪声相关系数的影响进行分析。

2.1.1 子阵阵元数的影响

当两个子阵的波束指向角都为90°时，子阵阵元数取1、3、6、9。按照公式(12)进行500次蒙特卡洛仿真，得到常规波束加权下噪声相关系数的仿真值；按照公式(19)计算常规波束加权下噪声相关系数理论曲线。如图3所示，随着阵元数增加，子阵间噪声相关系数随子阵中心间距的变化趋于平缓，四条曲线先是单调下降，最后在噪声相关系数为0附近呈振荡衰减并趋于0。可以看出，四条曲线的第一个零点，即子阵噪声相关半径分别为0.5、1.5、3、4.5个波长，此时，两个子阵组成的阵列是阵元总数为2M的均匀直线阵。也就是说，当两个完全相同的M元子阵通过常规波束形成指向90°时，子阵间的相关半径为0.5Mλ。

(a)M=1

2.1.2 子阵波束指向角的影响

固定子阵阵元数M=9，波束指向角θ从0°端射方向变化到90°正横方向。如图4所示，子阵波束指向角指向0°时，噪声相关系数随子阵间距波长比变化剧烈，类似衰减余弦曲线。随着波束指向角的增大，噪声相关性波动幅度减小且波动频率也减小，曲线更快趋于平稳。当波束指向90°时，噪声相关系数曲线随着间距波长比单调下降，在曲线第一次穿过零点后，逐渐趋近于0，振荡几乎消失。

(a)0°

为了进一步研究波束指向角对子阵噪声相关性的影响，采用Chebyshev加权方式进行对比，给定旁瓣级为-60 dB。同样按照公式(12)进行500次蒙特卡洛仿真，得到噪声相关系数的仿真值；分别按照公式(19)计算Chebyshev加权下噪声相关系数理论曲线。如图5所示，随着波束指向角的增大，和采用CBF加权时类似，噪声相关性函数趋于平缓且噪声相关半径逐渐增大，可以看出，此时影响噪声相关性的最重要因素为主瓣宽度。和图4相比，波束指向90°时，Chebyshev加权和CBF加权的主瓣宽度分别为36°和22°，主瓣宽度的增加导致噪声相关半径的减小，即零点更小，且波动幅度变小。

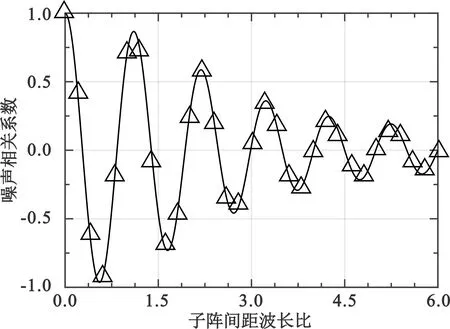
(a)0°

2.2 子阵噪声相关性对子阵波束形成的影响

假设空间各向同性均匀噪声场中，存在一个包含100个无指向性阵元的均匀直线阵。对阵列采用MVDR以及分子阵MVDR两种波束形成方法进行波束形成，并使波束指向端射方向。分子阵处理时，将阵列按阵元编号均分为10个子阵，每个子阵包含10个相邻无指向性阵元，子阵间无覆盖。对每个子阵进行MVDR波束形成，利用式(17)计算每个子阵输出噪声的互相关矩阵，再次对输出进行MVDR波束形成，最终得到一个总的加权系数向量。分别计算波束形成器的白噪声增益(White Noise Gain,WNG)，该指标反映了波束形成器对误差的敏感程度，其值越高，波束形成器越稳健。

如图6所示，MVDR波束形成过程中需要对100阶的阵元噪声协方差矩阵求逆，在阵元间距波长小于0.44时，阵元间噪声相关系数较大，使得噪声协方差矩阵近似奇异，从而引起100阶的噪声协方差矩阵求逆出现误差，导致波束形成性能急剧下降。对于子阵MVDR方法，子阵内阵元间10阶的噪声协方差矩阵求逆相对于100阶求逆，不容易出现奇异值和误差。但子阵间MVDR波束形成时，由于波束指向端射方向，根据图4(a)的规律，子阵间噪声相关系数波动较大。相邻两个子阵声学中心的间距为10倍阵元间距，当子阵声学中心间距位于子阵输出噪声相关系数绝对值最大值时，子阵间MVDR波束形成的WNG升高，使得子阵MVDR方法的指向性指数出现周期性凹槽，WNG出现周期性凸起。相比较于MVDR方法，本文方法稳健性较高，且指向性指数也维持在一个较高的水平。因此在划分子阵时，需要合适的子阵阵元数保证子阵内的噪声协方差矩阵求逆时不会出现奇异值，且需要考虑子阵波束指向对子阵输出噪声相关性的影响，从而保证子阵波束形成的性能。

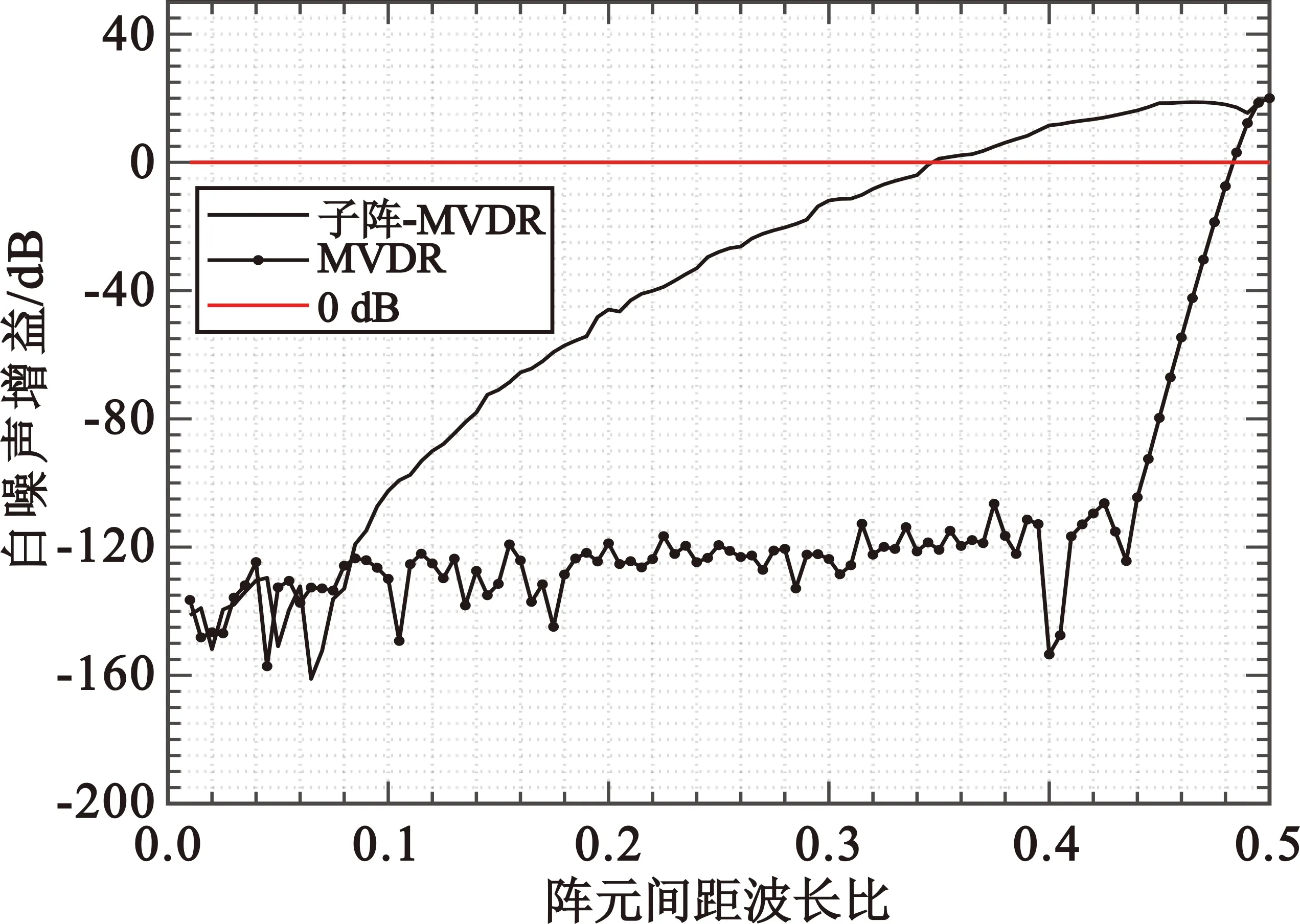
图6 100元均匀直线阵波束主瓣指向端射方向时两种波束形成的白噪声增益对比图

3 结 论

本文研究了子阵在空间各向同性均匀噪声场中输出噪声的相关性，给出了基于子阵加权向量的共线子阵在三维均匀噪声场中输出噪声相关系数的解析计算公式。利用该公式，分析了子阵不同参数对输出噪声相关性的影响，结果表明子阵阵元数、子阵波束指向角和子阵中心间距是影响子阵输出噪声相关性的最主要因素，而子阵波束旁瓣的影响较小。随着子阵间距的增大，输出噪声相关性总体上趋近于0。主瓣宽度决定了相关系数随间距变化曲线的衰减强弱，主瓣宽度越宽，噪声相关系数随子阵间距变化曲线的波动幅度越小，两个子阵的噪声相关半径越小。波束指向和阵列端射方向夹角决定了相关系数变化曲线的波动频率，夹角为0°时波动频率最大，相关系数波动最为剧烈；随着夹角的增大，当夹角为90°时，噪声相关系数曲线波动最小，几乎单调下降到0附近。针对共线线列子阵的噪声相关性分析，进行了蒙特卡洛仿真，结果验证了本文理论的正确性。随后进一步对子阵波束形成进行了数值仿真，结果表明通过子阵处理，可以有效提高MVDR波束形成的稳健性。