一种数字调制信号符号速率盲估计方法*

谢纪岭，卢彦卿

(南京中新赛克科技有限责任公司，南京211153)

0 引 言

符号速率是数字调制信号的独有特征，因此可以作为调制方式识别中区分模拟调制和数字调制的有效特征参量，准确估计符号速率也是非合作接收系统中正确解调的前提和关键。目前为止，符号速率估计方法归纳起来主要有基于小波变换的符号速率估计算法[1-4]、基于循环自相关和循环谱的符号速率估计方法[5-11]两类。基于平方谱的符号速率估计方法[12]本质上是简化的共轭循环自相关法，基于延时相差的码元速率估计算法[13-14]和基于信号包络平方谱的符号速率估计算法[15-17]实际上是简化的循环自相关算法，它们仅仅计算某个或某几个特定时延的共轭循环自相关或循环自相关，然后根据离散谱线估计符号速率。小波变换类方法受脉冲成形滤波器和小波函数、小波尺度等因素的影响较大，而循环自相关和循环谱及其各类简化算法由于其通用性受到更多青睐，这类算法几乎不需要任何先验信息即可实现符号速率的盲估计，但其不足是循环自相关和循环谱计算需要较多采样数据，并且其计算复杂度较大。其他简化算法都是围绕这两大缺点在牺牲一定性能的前提下进行的优化。

本文在根据信号功率谱获得信号带宽的粗略估计值之后，根据带宽调整数据的采样速率，设置循环自相关计算的时延范围，利用快速傅里叶变换(Fast Fourier Transformation，FFT)算法计算信号的循环自相关，对不同时延的循环自相关结果进行累加，采用文献[17]类似的方法对累加结果进行滤波处理以突出符号速率离散谱线，获得符号速率的估计值。但文献[17]中并没有给出滤波长度的取值，也没有给出离散谱线的判决准则。

1 数字调制信号的通用模型

最常见的基本数字调制方式主要有幅移键控(Amplitude Shift Keying，ASK)、相移键控(Phase Shift Keying，PSK)、频移键控(Frequency Shift Keying，FSK)和正交幅度调制(Quadrature Amplitude Modulation，QAM)，其中，ASK、PSK和QAM调制属于线性调制，其调制信号波形的通用表达式是

(1)

2 信号的循环自相关

对于ASK、PSK和QAM等线性调制，接收端对接收到的信号进行正交下变频处理后的信号可表示为

(2)

式中：fI为正交下变频处理后的残留频差，n(t)为复噪声。假设噪声和信号之间不相干，则接收信号y(t)的自相关函数

Ryy(t,τ)=E{y(t+τ)y*(t)}=

ej(2πfIt+φ1)]*}+σ2δ(τ)=

g(t+τ-mTb)g(t-nTb)·ej2πfIτ+σ2δ(τ)。

(3)

当ASK、PSK和QAM调制星座图中的星座点独立等概分布时，

(4)

所以，接收信号y(t)的自相关函数

(5)

由上式可知，

Ryy(t,τ)=Ryy(t+Tb,τ)。

(6)

因此，Ryy(t,τ)是以Tb为周期的周期函数，y(t)是循环平稳信号，其循环频率为{α=k/Tb,k∈}，循环频率α对应的循环自相关为

(7)

从上式可以看出，ASK、PSK、QAM等线性调制信号的符号速率对应其循环频率的基频和循环频率的间隔，因此可以通过搜索循环自相关中的离散谱线获取符号速率。

3 符号速率估计

利用循环自相关估计调制信号的符号速率时，首先需要计算自相关函数，然后通过傅里叶变换计算不同时延对应的循环自相关值，再把不同时延对应的循环自相关幅值进行累加，对累加结果进行非线性滤波以突出循环频率谱线，搜索谱线并与预先设定的门限相比，如果超过门限则判为有效谱线并得到符号率，否则认为没有估计出符号率。整个算法的运算量主要集中在循环自相关的计算上，因此，时延的个数与计算量几乎成正比。然而，由于调制时几乎都使用了抑制带外泄漏的成形滤波，导致时延超过Tb时g(t+τ-nTb)g(t-nTb)的值很小，对估计性能的提升较小。所以，选择合适的时延取值范围可以在对性能影响很小的情况下有效降低运算复杂度，但符号周期Tb是待估计量。实际非合作接收处理时，通常首先对采样数据进行功率谱估计，根据功率谱检测信号并估计信号的带宽和中心频点，然后根据中心频点和带宽进行采样率转换，使得转换后的过采样因子基本恒定。对于ASK、PSK和QAM调制而言，调制信号带宽与符号率之间存在确定关系，因此获得带宽的粗略估计之后就可知道符号周期的大致范围，然后就可以确定计算循环自相关的时延取值范围。计算得到自相关函数之后，通过FFT计算循环自相关函数，可以有效降低计算复杂度；估计得到多个时延对应的循环自相关Rα(τ)后，将不同时延对应循环自相关的幅值相加，获得不同循环频率对应的幅值R(k)，然后进行非线性滤波，得到R′(k)：

(8)

式中：w为平均窗长，其取值与R(k)的数据长度N和过采样倍数Nov的估计值有关，平均窗长w通常可取为N/(16×Nov)～N/(32×Nov)之间。对滤波后的R′(k)计算除零频外的均值σm，然后找出超过β倍的均值βσm的谱线，该谱线记为符号速率谱线，β的取值可通过仿真确定。设符号率谱线的位置为n，循环自相关数据长度为N，数据的采样率为Fs，则符号率的估计结果为

由上式可知，采用上述方法进行符号速率估计的精度取决于数据的采样率Fs和循环自相关数据的长度N，其最大误差为Fs/2N。因此，通常采用符号率谱线的正确检测概率来衡量这类方法的性能。

4 计算机仿真和实测数据验证

由于ASK和PSK都可以看成是QAM调制信号的特例，因此针对16QAM调制信号进行仿真。设符号速率为25 000 symbol/s，接收端正交下变频后的残留频偏为9 kHz，采样频率为200 kHz，发送端采用滚降系数为0.35的根升余弦滤波器，采样数据长度为65 568，计算循环自相关的时延取值范围为[-16Ts,16Ts]，Ts为采样间隔。从仿真参数设置可知，过采样率为8 MHz，每个时延计算得到的循环自相关数据长度为65 536。带内信噪比为5 dB时的功率谱如图1所示，对应的循环自相关函数如图2所示，不同时延的循环自相关累加后如图3所示，非线性滤波后的循环自相关累加值如图4所示。AWGN信道下，k取值为3时，在每种信噪比下进行10 000次仿真，符号率正确估计概率随带内信噪比的变化关系如图5所示。同时将文献[16]中使用平方变换进行符号率估计算法的结果也进行了对比仿真，值得注意的一点是本仿真中的信噪比是指带内信噪比。

图1 16QAM调制信号功率谱(带内信噪比5 dB)

图2 16QAM调制信号循环自相关(带内信噪比5 dB)

图3 16QAM调制信号非线性滤波前循环自相关累加

图4 16QAM调制信号非线性滤波后循环自相关累加

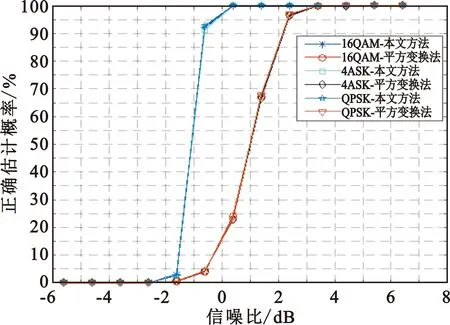
图5 符号速估计随带内信噪比变化关系

为了进一步验证算法的有效性，使用信号源发射各种数字调制信号进行测试，实际测试结果与仿真结果基本一致。限于篇幅，仅给出BPSK调制信号的部分结果。符号速率设置为1 Msymbol/s，数据采样率为8 MHz，BPSK对应的功率谱、循环自相关和不同时延循环自相关叠加并滤波后的波形如图6～8所示。

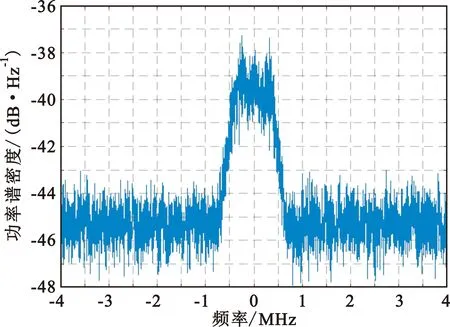
图6 信号源发射BPSK信号的功率谱

图7 信号源发射BPSK信号的循环自相关

图8 信号源发射BPSK信号循环自相关叠加和滤波后的波形

5 结束语

针对数字调制信号的符号速率估计，本文提出了一种循环自相关和非线性滤波相结合提取符号率谱线的估计方法。通过估计信号的功率谱获得信号带宽的粗略估计，然后根据带宽调整数据的采样速率，设置循环自相关计算的时延范围，利用FFT算法计算信号的循环自相关，对不同时延的循环自相关结果进行累加，对累加结果进行滤波处理以突出符号速率离散谱线，然后与预设门限进行比较，获得符号速率的估计值，几乎不需要任何先验信息即能完成符号速率的估计。但循环自相关类方法在微弱信号特征参数估计、带一定程度失真时的信号特征参数估计以及多信号、频谱部分重叠时的信号特征参数估计方面有待进一步研究。