速度脉冲地震下偏心重力柱-核心筒结构的弹塑性地震响应分析

马晓宇，补国斌，熊浩然，徐 冲，汪 恒，张 哲

（湖南工业大学 土木工程学院，湖南 株洲 412007）

0 引言

近年来，偏心建筑结构发展迅速，其抗震研究和应用也得到了快速发展。国内外专家学者们对偏心结构的抗震性能进行了广泛的研究。如Bu G.B.等[1]对强度偏心框架结构的地震易损性进行了分析。夏玲涛等[2]对双向偏心结构实用抗震计算方法进行了研究。补国斌[3]针对偏心框架结构体系的抗震性能和设计方法展开了详细研究。但是已有研究大多数是针对传统结构体系进行的研究。虽然周靖等[4]提出了一个新型重力柱-核心筒结构体系，并开展了相关的地震模拟振动台试验研究和数值分析，但是尚未对其偏心体系展开进一步分析。因此，本研究将以此新型重力柱-核心筒结构为研究对象，开展其在偏心布置下的抗震性能研究。

历次震害分析结果表明，相对于非速度脉冲型地震动，速度脉冲型地震动对结构产生的影响更强，更易使建筑物倒塌和破坏。国内外大量的研究结果表明，结构在速度脉冲地震下的层间剪力、位移和延性需求等动力响应较非脉冲情况的显著增大[5]。但是大多数有关速度脉冲地震的研究均停留在对规则和对称结构的研究上，而考虑速度脉冲地震效应和偏心综合影响的研究较少[6]，且尚无考虑速度脉冲地震和偏心双重不利因素对新型重力柱-核心筒结构体系抗震性能影响研究的报道。

针对已有研究中的不足，本研究主要考虑在速度脉冲地震与结构质量偏心双重不利条件下，新型重力柱-核心筒结构的弹塑性地震响应变化规律，重点探讨双重不利条件对顶点位移、层间剪力、层间位移和层间扭矩及扭转角的定量影响规律。

1 偏心重力柱-核心筒结构模型

1.1 重力柱-核心筒结构振动台试验简介和数值模拟

新型重力柱-核心筒结构体系利用核心筒具有的抗侧、抗扭刚度大的优势，将结构外围框架柱、内筒剪力墙与钢梁的连接节点由刚接改为铰接，将外框架设计成只承受重力荷载的重力柱，而水平荷载由核心筒承担，这样能使结构受力更明确，不用纠结外框架剪力比的调整，简化设计过程、提高结构设计的灵活性。新型体系极大地减少了施工现场的焊接工作量，有半工业模块化建造特点，为建筑结构形式创新提供了灵活性。

文献[4]以混凝土重力柱-核心筒结构的实际工程——广西金融大厦为背景，开展了1:50 缩尺地震模拟振动台试验研究（其结构模型见图1），结构构件典型的损伤情况如图2所示，试验模型和数据的详细介绍参见文献[4]，本文从略。

图1 振动台试验结构模型Fig.1 Structural model of the shaking table test

图2 典型构件损伤情况示意图Fig.2 Schematic diagram of typical component damages

本研究以该试验对应的原型结构为基础开展研究。原型结构的总高度为320 m，共37 层，其他构件配筋、荷载条件、地震输入等详细信息参见文献[7]。并采用李康宁博士开发的结构静动力非线性分析软件CANNY[8]对结构进行地震响应分析。CANNY 软件使用有限元、线单元和特殊单元表达结构的力学特性，基于塑性理论建立单元力和变形关系，采用数值积分逐步求解法模拟结构物在各种静力/动力荷载作用下变形、损伤和破坏的全过程。关于CANNY 软件更详细的介绍，参见文献[8]。

采用CANNY 软件对原型结构进行数值建模，得到如图3所示的有限元模型。

图3 结构的CANNY 有限元模型Fig.3 Finite element model of CANNY of the structure

本研究中，选用的混凝土强度等级为C60，钢筋级别为HRB335 和HRB400，详细参数等见文献[7]。钢筋和混凝土的本构关系模型分别采用CANNY 中的SR4 模型和CS4 模型进行表达，材料参数的符号说明详见文献[8]，参数取值采用程序建议的默认值（材料本构关系模型如图4所示）。将试验用地震波按相似比转换为原型结构的地震记录，并作为地震动输入，对该原型结构进行非线性动力时程分析，得到模拟结果。然后对模型试验结果按相似比转换为原型试验结果。选取7 度小震、中震和大震数据进行对比分析，所得结果如图5所示。由图5可以得知，模拟结果和试验结果吻合度较高，表明建模和参数设置合理，故可以采用同样的参数设置进行下文的数值扩展参数化分析。

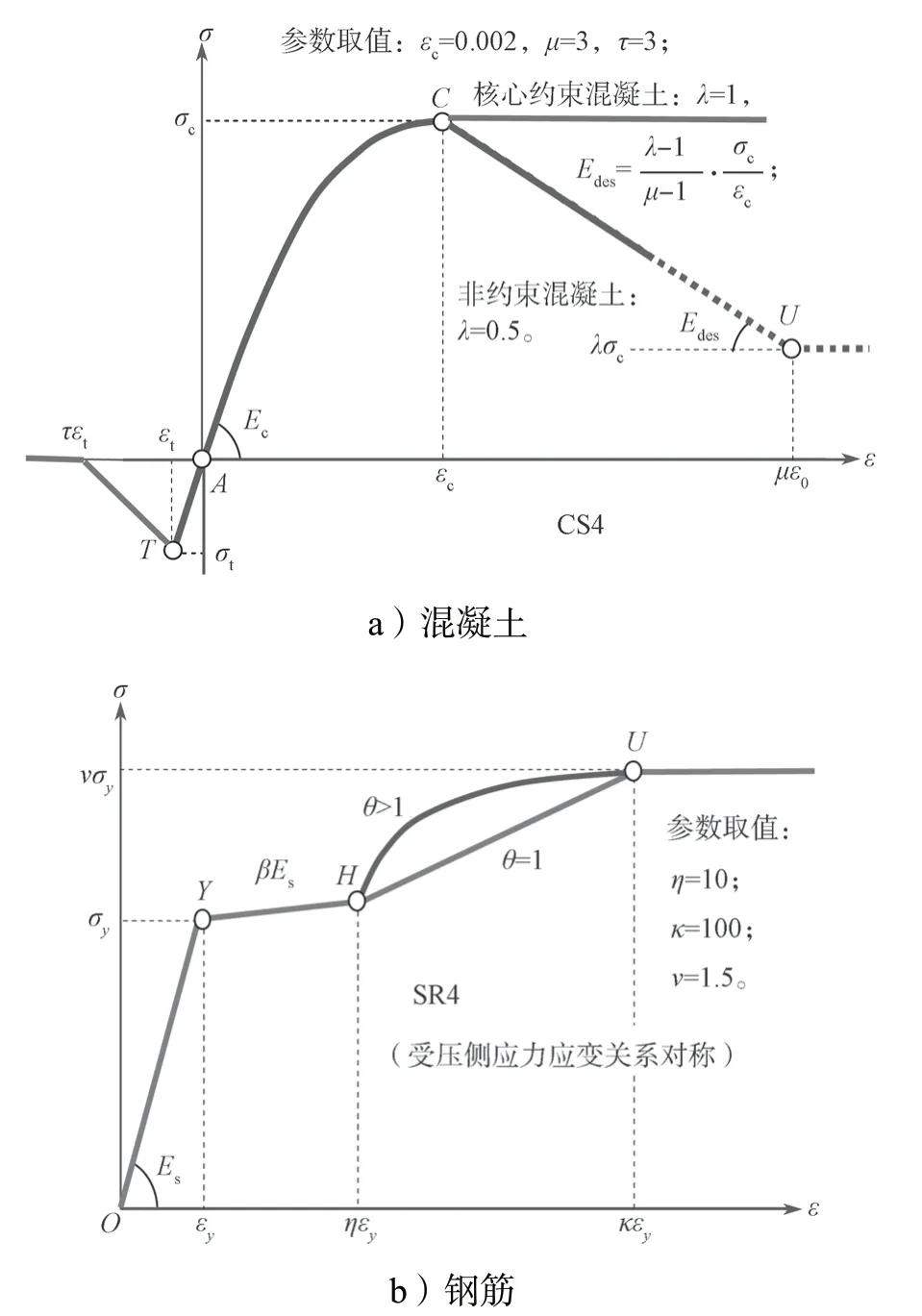
图4 材料的本构关系模型Fig.4 Material constitutive relation model

图5 不同震级下的位移时程比较Fig.5 Comparison of displacement time history under different earthquake magnitudes

1.2 偏心重力柱-核心筒结构建模

以上文给出的新型重力柱-核心筒结构为基准结构，通过调整左右侧质量，得到偏心体系，图6为对称结构与偏心结构的平面示意图。

图6 对称结构与偏心结构平面示意图Fig.6 Plane diagram of symmetric and eccentric structure

本模型分析中仅考虑沿x轴单向偏心（因结构对称，沿y轴单向偏心情况与x轴相同），即左侧各节点的质量减小，右侧各节点的质量增大，但调整后结构的总质量保持不变。结构偏心率的计算公式如下：

式中：xi为第i根柱或者墙质心相对于几何中心的横坐标；

L为结构沿偏心方向的总长度；

e为质量偏心距。

前期研究结果表明[3]，在竖向布置上，各层均匀偏心体系相对于其它偏心体系的地震需求更大，更为不利，所以本研究选取各层均匀质量偏心体系来进行研究与分析。

2 地震动输入与分析方法

2.1 地震动输入

历次震害表明，速度脉冲地震作用相对于非速度脉冲地震作用，将对结构造成更大的速度和位移冲击。选取表1所列3 条近场速度脉冲型地震加速度记录，编号P1~P3，速度脉冲特性用基于速度和能量标定的脉冲指标（PI）[9]表征。同时，选取对应的3 条非速度脉冲记录作为对比，编号为N1~N3，详细的地震记录数据参见文献[9]，此处不再列出。为强调地震作用的随机性和不确定性，表中所列内容均采用原始加速度记录。

表1 选取的3 条速度脉冲型地震动记录Table 1 Three selected velocity pulse ground motion records

2.2 分析方法

结合前期振动台试验数据，综合考虑速度脉冲强震和结构偏心耦合效应，对偏心重力柱-核心筒结构体系进行弹塑性地震响应演化规律分析。

基于1.2 节的结构模型和2.1 节的地震动记录，采用CANNY 程序，依据以下条件进行非线性动力时程分析：4 种偏心率（0, 0.1, 0.2, 0.3 分别代表无偏心，小、中、大偏心程度）；6 条地震加速度记录（3条速度脉冲型地震和对应的非速度脉冲型地震）。地震作用为y轴方向，偏心沿x轴方向。峰值地面运动加速度取0.5g，保证各结构模型均进入弹塑性受力阶段和变形阶段。

3 弹塑性地震响应分析

分析结果表明，脉冲工况和非脉冲工况下，各条地震波下得到的规律具有一致性。因此，3.1 节仅以脉冲和非脉冲的第一条地震波为例进行分析和对比，其他工况规律类似。3.2 至3.3 节则采用两种地震工况下3 条地震波得到的计算结果平均值来表征结构的整体地震响应。以下各图中 “P”和“N”分别表示速度脉冲地震工况和非速度脉冲地震工况（以下分别简称脉冲工况和非脉冲工况）。“e”表示偏心率，图中“P1-e=0”表示第一条速度脉冲地震工况下偏心率为0 时的曲线。

3.1 单条地震波作用下的顶点位移时程分析

图7分别给出了P1 与N1 工况下不同偏心率结构的顶点位移时程变化曲线。

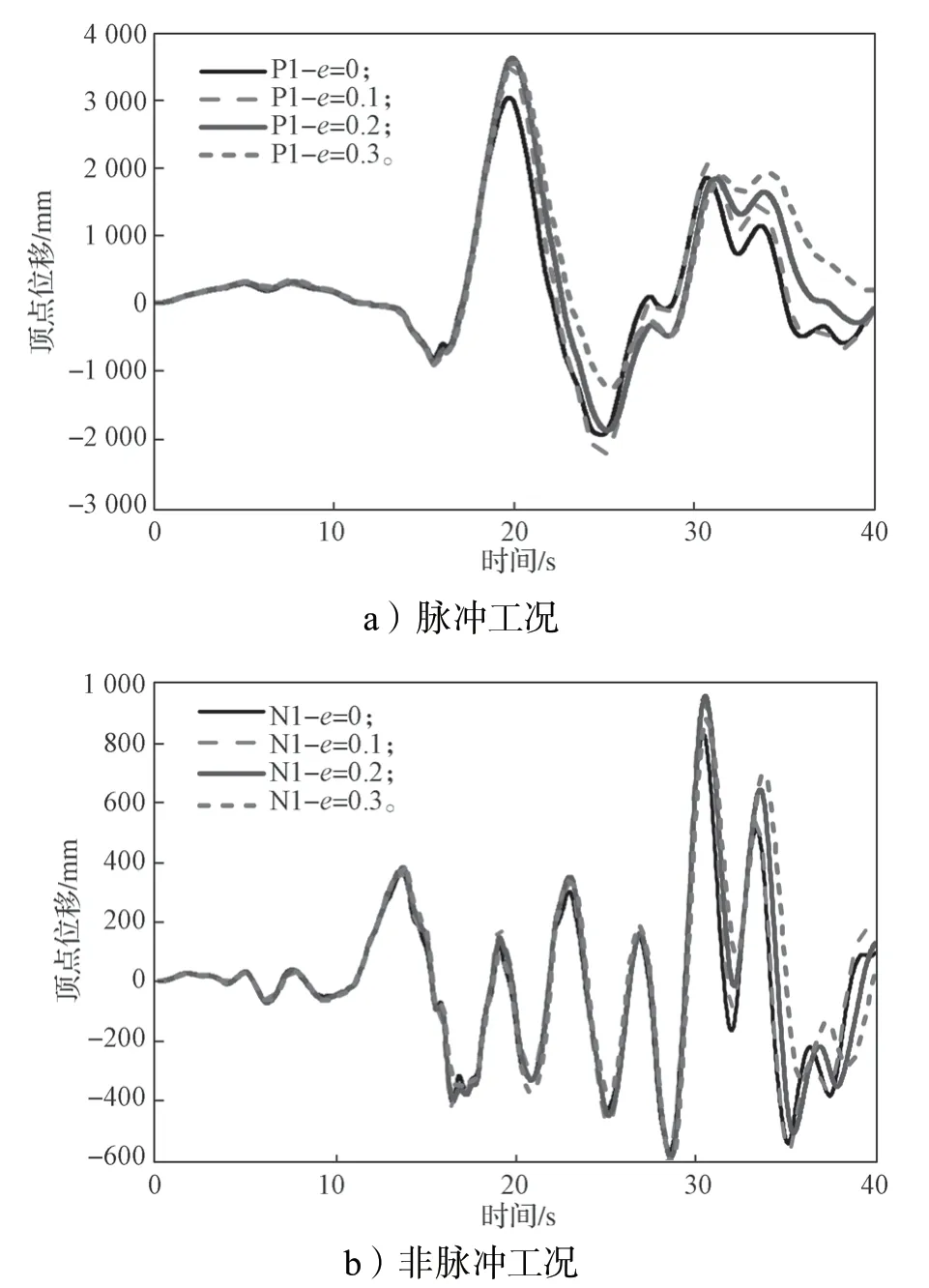
图7 不同工况下各结构的顶点位移时程曲线Fig.7 Vertex displacement time history curves of the tube structures under different conditions

由图7可知，同一时间的顶点位移最大值随着偏心率增大表现出增大的变化趋势。这一现象表明，偏心率越大，对结构顶点位移的影响也越大。此外，通过两工况下的曲线对比可以看出，在脉冲工况下，结构的最大顶点位移接近4 000 mm，而非速度脉冲工况下的最大顶点位移仅接近1 000 mm，约为速度脉冲工况下的1/4。由此可以得知，速度脉冲型地震对结构顶点位移的影响要远大于非速度脉冲型地震对结构顶点位移的影响。

3.2 偏心和速度脉冲效应对最大层间剪力和最大层间位移角的影响

非线性动力时程分析所得偏心率和速度脉冲效应对最大层间剪力的影响曲线如图8所示，其中图8a 为脉冲和非脉冲工况下，不同偏心率结构各楼层最大层间剪力的变化规律。

观察图8a 中的曲线可知，两种地震工况下，各层的层间剪力包络线均随着偏心率的增大有内收的变化趋势。此规律与文献[10]的结论类似。可能的原因是随着偏心率增大，扭转效应加大，与地震输入垂直的另一方向也随之分担了部分剪力作用，导致沿地震方向的层间剪力减小。另外，当偏心率相同时，脉冲工况下各楼层的层间剪力包络线位于非脉冲工况下包络线以外。

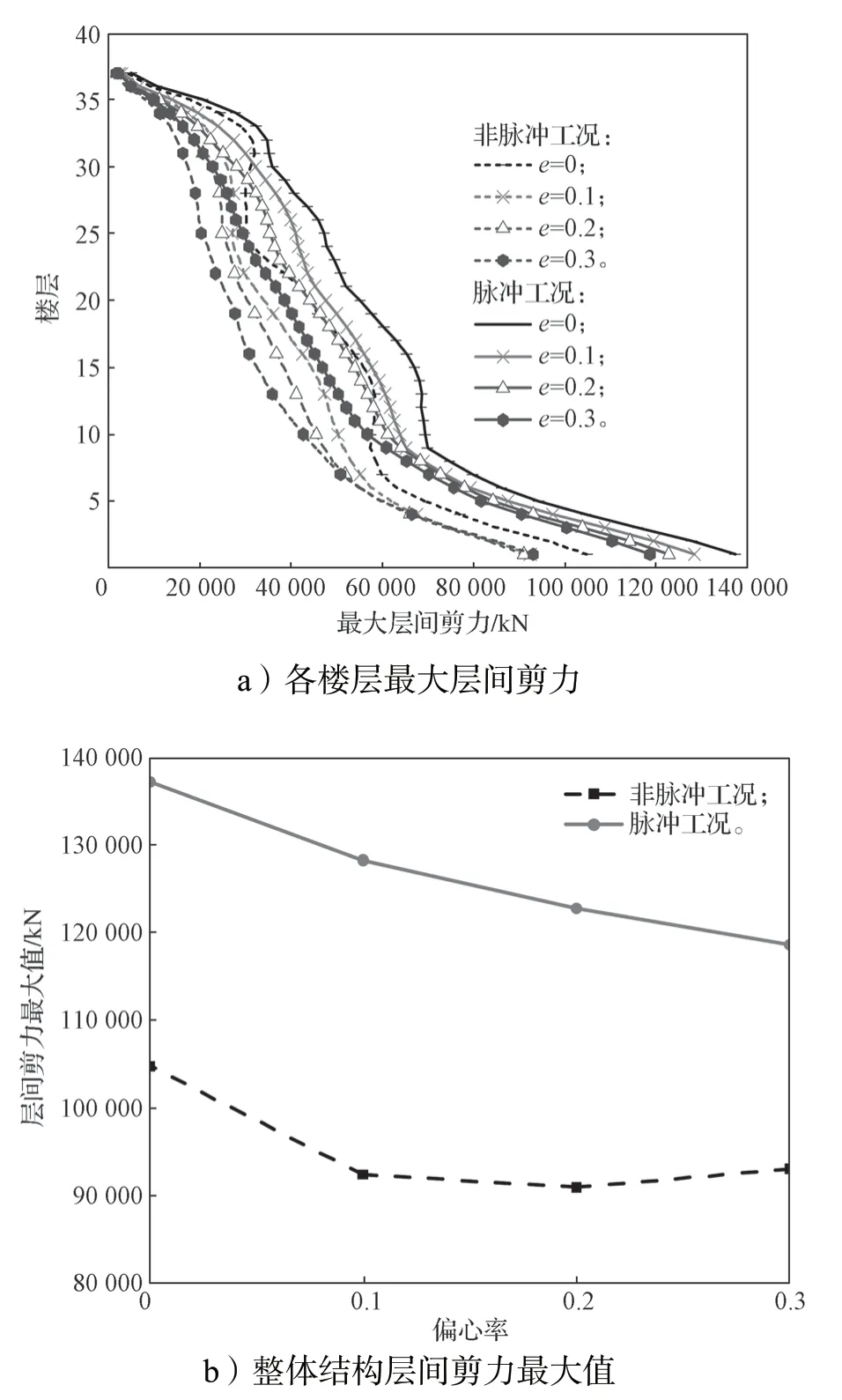
图8 不同工况下的最大层间剪力变化规律曲线Fig.8 Change trend curves of the maximun inter-story shear force under different conditions

为了定量分析偏心率和速度脉冲地震效应的影响，进一步给出了整体结构最大层间剪力值（取各楼层最大层间剪力的最大值）随偏心率的变化规律，如图8b 所示。

由图8b 中的曲线可以得知，两种地震工况下，整体结构的层间剪力最大值均随偏心率增大有减小的变化趋势。当偏心率由0 变为0.3 时，脉冲工况和非脉冲工况下的最大层间剪力值分别减小了15%和17%。而偏心率一定时，脉冲工况下的整体结构最大层间剪力值显著高于非脉冲工况下的对应值。如当偏心率均为0.1 时，脉冲工况下的层间剪力约是非脉冲工况下层间剪力的1.4 倍。

非线性动力时程分析所得偏心率和速度脉冲效应对最大层间位移角影响的规律曲线如图9所示。其中，图9a 表示不同偏心率下，结构在脉冲和非脉冲工况下各楼层最大层间位移角的变化规律曲线；图9b 为取各条曲线的层间位移角的最大值进行定量分析所得的变化规律曲线。

图9 不同工况下的层间位移角变化规律曲线Fig.9 Change trend curves of the inter-story drift ratios under different conditions

从图9a 所示楼层最大层间位移角变化曲线可以看出，在脉冲和非脉冲两种工况下，楼层最大层间位移角随着偏心率增大有增大的变化趋势。此外，脉冲工况下的最大层间位移角要远大于非脉冲工况下的。由图9b 可以得知，在脉冲和非脉冲两种工况下，楼层层间位移角的最大值均随着偏心率增大有增大的变化趋势，当偏心率由0 变化到0.3 时，脉冲工况和非脉冲工况下的最大层间位移角分别增大了24%和18%。另外，在相同偏心率条件下，脉冲工况下的最大层间位移角明显远大于非脉冲工况下的。如当偏心率为0.1 时，脉冲工况下的层间位移角最大值约是非脉冲工况下的3 倍。

3.3 偏心和速度脉冲效应对最大层间扭矩和最大层间扭转角的影响

非线性动力时程分析所得偏心和速度脉冲效应对最大层间扭矩的影响结果如图10 所示。其中，图10a 是不同偏心率下，结构在脉冲和非脉冲工况下各楼层间扭矩值的变化曲线，图10b 为提取各工况下整体结构的层间扭矩最大值分析曲线。

图10 不同工况下的层间扭矩变化规律曲线Fig.10 Change trend curves of the inter-story torsion under different conditions

由图10a 中的楼层最大层间扭矩曲线可看出，在所有工况下，最大层间扭矩均随偏心率的增大而减小，最大层间扭矩值均在靠近底部出现。由图10b可知，在同种工况下，随着偏心率增大，层间扭矩最大值随之增大，且呈现先线性急剧增长后非线性缓慢增长的发展趋势。这是由于随着偏心率增大，扭转效应加大，出现了耦联现象。同时，在其余条件相同的情况下，脉冲工况的层间扭矩比非脉冲工况大。如偏心率为0.3 的情况下，脉冲工况下的底层扭矩约为非脉冲工况下的1.2 倍。

非线性动力时程分析所得偏心率和速度脉冲效应对最大层间扭转角的影响结果如图11 所示。其中图11a 为不同偏心率下，结构在脉冲工况和非脉冲工况下各楼层最大层间扭转角的变化曲线，图11b 为各工况下整体结构层间扭转角最大值变化曲线。

图11 不同工况下的层间扭转角变化规律曲线Fig.11 Change trend curves of the inter-story rotation under different conditions

由图11a 可以看出，最大层间扭转角的变化规律与最大层间位移角的变化规律类似，但是其最大值出现在结构顶部附近。由图11a 还可以得知，各楼层最大层间扭转角随着偏心率增大而增大，脉冲工况下的包络曲线明显比非脉冲工况下的外扩。由图11b 可知，当偏心率相同时，脉冲工况下的层间扭转角最大值明显大于非脉冲工况下的。如当偏心率为0.3 时，脉冲工况下的最大层间扭转角是非脉冲工况下的2.8 倍左右。此外，同种工况下，层间扭转角最大值随着偏心率的增大不断增大，且增幅较大，总体上呈现出线性增长的变化趋势。

4 结论

通过对重力柱-核心筒结构在速度脉冲地震和偏心耦合条件下的地震响应分析，得到以下主要结论：

1）重力柱-核心筒结构的顶点位移随着偏心率的加大有增大的变化趋势，速度脉冲地震作用下（脉冲工况）的顶点位移极值远高于非速度脉冲地震下（非脉冲工况）的对应值。脉冲工况的顶点位移极值约为非脉冲工况的4 倍。故对结构的弹塑性分析中，应重点关注速度脉冲地震效应。

2）各楼层最大层间剪力随着偏心率的增加而减小，而各层间位移角则表现出相反的变化趋势。脉冲工况和非脉冲工况下，当偏心率由0 变化到0.3 时，层间剪力最大值分别减小了15%和17%，最大层间位移角分别增大了24%和18%。当偏心率一定时，脉冲工况下的层间剪力最大值和层间位移角最大值均显著高于非脉冲工况下的对应值。当偏心率为0.1时，脉冲工况下的层间剪力最大值和层间位移角最大值分别是非脉冲工况下层间位移的1.4 倍和3.0 倍。因此，速度脉冲地震作用下，位移的增大效应比力的增大效应更为明显。

3）各楼层最大层间扭矩和最大层间扭转角均随着偏心率的增加而增大。随着偏心率加大，层间扭矩最大值表现出先线性增长后非线性增长的变化趋势，层间扭转角最大值则表现出大致成线性增长的变化趋势。当偏心率一定时，脉冲工况下的层间扭矩最大值和层间扭转角最大值均显著高于非脉冲工况下的对应值。如当偏心率为0.3 时，脉冲工况下的层间扭矩最大值和层间扭转角最大值分别是非脉冲工况下的1.2 倍和2.8 倍。