无人机图像矫正方法在河流表面流速测量中的应用

刘炳浩，柳权奎

（1.湖南工业大学 土木工程学院，湖南 株洲 412007；2.东义大学 土木工程系，韩国 釜山 47340）

1 研究背景

天然河流的水文检测是洪水及地质灾害预防措施的重要组成部分，水文基础研究和水利工程应用均需要河流实测资料作为基础支撑[1]。在河流水文检测工作中，流速和流量是两个重要的要素。其中，流速是推求流量的必要参数，流量是水文测量和水资源管理中最常用的量化指标，精确的流量预测对洪水预测和水文过程研究等均具有十分重要的意义。

现有的流速测量设备大体上可以分为接触式和非接触式两类。接触式流速计包括螺旋桨流速仪和多普勒声学流速仪等，这类流速计需要接触水体以测量流速；非接触式流速计包括雷达流速仪、超声波流速仪等，其无需接触水体即可完成流速测量。其中，基于影像分析的影像流速仪是一种较为先进的流速测量手段，在洪水等难以接触水面的条件下，也能迅速准确地获得整个河流表面的流速分布。与其他非接触式测定法相比，影像流速测定具有测试精确度高、速度快、成本低、安全性高等特点[2]。在诞生后的20 多年里，影像测速使用的设备从最初的固定摄像头向便携式摄像机、热成像摄像机、智能手机等拓展，发生了非常多样的变化。

近年来，随着无人机技术，特别是小型低空无人机技术的快速发展，通过无人机获取地面影像的方法被广泛应用于应急救援、地形测定、林业管理、农业灾害检测、海洋污染检测、输电线路巡查等领域。无人机摄影是一种有效、便捷的影像收集手段，由于其可以获取垂直向下的拍摄角度，同时拍摄者可以远离危险和难以接近的区域遥控拍摄，因此其在水文测量方面也具有明显的优势。

1.1 研究现状

随着河流表面图像测速技术（river surface image velocimetry，SIV）的发展，各种SIV 技术的载体也一起被开发出来，如固定式SIV 流速计、移动式SIV流速计、红外线SIV 流速计、手机SIV 流速计等。然而，地面上摄像机拍摄的影像有一个共同的问题，其近、远端的分辨率相差较大，这是测量误差发生的主要原因之一。为了解决这一问题，K.Takehara等[3]使用直径15 cm 的煎饼作为示踪物，乘坐直升机对河面进行了现场拍摄和分析，获取的流速测量结果（1.1 m/s）与I.Fujita 等[4]安装在地面上的摄像机获取的结果（1.3 m/s）较为接近，二者对地面标定点的定位标准误差为12.8 cm，由此可见测定的结果比较准确，但是成本较高。相对于直升飞机，无人机拍摄成本更低，且更为便捷。Yu K.等[5-6]开发了一种基于无人机影像的表面图像测速仪，该测速仪添加了远红外热成像摄像头，可以兼顾夜间使用。F.Tauro 等[7-9]评估了四旋翼无人机的悬停能力，提出了保持相机垂直于水面以避免获取GRP 的设想，并于2016年在意大利阿尔卑斯山脉的一条山间溪流的两个不同地点进行了无人机和固定LSPIV（largescale particle image velocimeter）装置的表面流速检测对比试验，试验结果表明：与传统的LSPIV 实现相比，来自航空平台的测量对示踪剂的移动更敏感，结果更接近准确值。同时，无人机稳定悬停的稳定性对检测结果影响较大，高效率的图像分析手段、无人机高精度的定位能力有可能降低对无人机悬停能力的需求。Q.W.Lewis 等[10-12]分别用无人机和固定摄像机采集视频，利用LSPIV 在美国伊利诺斯州的10 个不同的河流位置进行了流量测量，将测量结果与声学多普勒流速计、螺旋桨流速计和已建立的流速计测量的参考值进行了比较，并评估了基于小型无人机系统（small unmanned aerial systems，sUAS）的LSPIV 测量二维平均表面速度以及从连续图像获取的准瞬时二维速度的准确性，评估结果认为：对于持续二维流动，基于sUAS 的LSPIV 方法得到的平均速度与固定摄像机平台得到的速度一致，两种方法测量的速度与声学多普勒测速仪测量的近地表速度一致。

以上研究成果证实了基于sUAS 的LSPIV 能提供精确的、高分辨率的连续二维流场大尺度区域的平均表面速度测量结果，并且可以观测二维流场结构的演变，是一种有价值的绘制河流表面流场二维图像的新方法。

1.2 现存问题

利用无人机影像测量河流表面流速的方法仍存在以下问题：

1）无人机晃动对测量结果的影响很大。在大风等极端天气下，无人机很难保持静止，无人机自身的晃动会造成被摄物体在视频中晃动，这种晃动会直接影响流速测量结果。尤其是对大河的测量中，由于无人机需要飞行得更高，少量的晃动就会造成地面上物体出现较大的位置偏差。

2）测量准备工作繁琐。现有的方法大多需要人为设置地面参照点，并对参照点进行定位测量，然后借助参照点矫正图像。这种方法需要大量的准备工作，且测量时间长、效率低。同时，很多自然河流的河岸是难于接近的，这为参照点的设置和测量带来了诸多不便。

为了解决无人机晃动带来的问题、简化测量过程，实现快速、安全、精准的河流表面流速测量，本文拟开发一种基于无人机飞行记录信息的图像矫正方法，在不对参照点进行现场测量的情况下实现对河流表面流速的精准测量。此外，还尝试了不设置参照点，仅通过飞行记录来矫正图像的方法，并分别在试验河道与自然河道进行了现场测量验证。

2 图像的正射矫正

2.1 矫正方法

2.1.1 使用参照点的情况

具体的图像矫正流程如图1所示，在河流两岸设置4 个以上的参照点，先根据矫正后的图像上参照点的像素坐标(u,v)相对于图像光学中心点像素坐标(u0,v0)的位置，利用共线条件式（式1）计算出参照点的空间坐标(xi,yi)，然后根据输出图像的尺寸设置一个缩放系数n(pixel/m)，令每个参照点在输出图像上的像素坐标(xi,yi)=(nxi,nyi)。最后利用待矫正图像中的参照点像素坐标对图像进行单应性变换，即可获得矫正后的图像。

图1 使用参照点时的图像矫正流程示意图Fig.1 Image correction flow diagram using reference points

本研究飞行高度约为20 m 左右，选用了直径为18 cm 的红色圆形纸片贴在碟子上作为参照点，如图2所示。

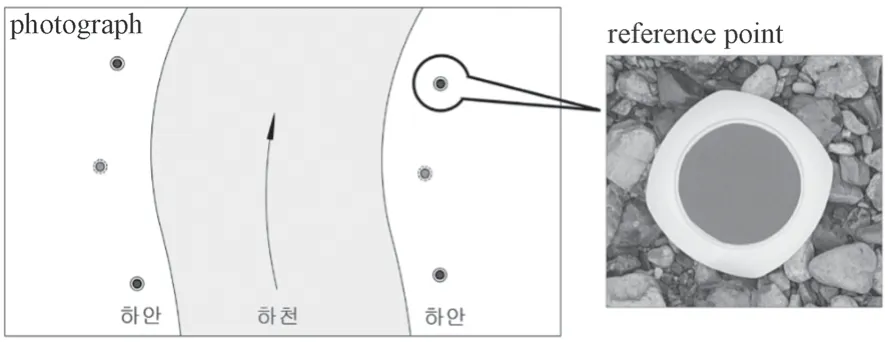
图2 参照点设置示意图Fig.2 Schematic diagram of reference point setting

因为此处需要用参照点的像素坐标求解空间坐标，因此用共线条件式的逆变换式：

式中：c为相机的焦距；(u,v)为照片中光学中心点的坐标，可通过相机标定获取；(XW,YW,ZW)为相机光学中心位置的空间坐标；aij为相机的旋转矩阵R（式3）的元素；后两项可通过无人机的飞行记录获取。

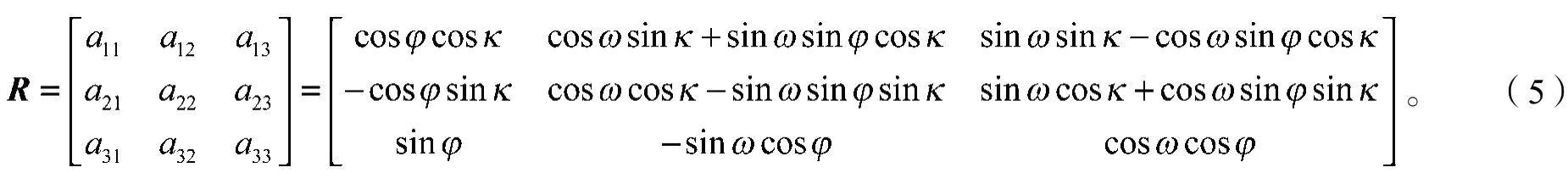
式中：ω、φ、κ分别为相机坐标系绕着X、Y、Z轴旋转的旋转分量。

2.1.2 不使用参照点的情况

由于在自然河流流速测定中，往往很难在河岸附近设置参照点。另外，在对大河的流速测定时，由于无人机飞行高度较高，因此如果参照物较小，识别度就会下降，必须使用较大的参照物，这给测量流速增加了不便。因此，如果不用参照点，而直接根据无人机的位置、高度、姿态等信息，通过对图像的平移、缩放和三维旋转等矫正图像，可极大减少工作量，提高测量效率。

2.2 获取外部参数

获取相机外部参数的方法通常有以下两种：

1）通过EXIF（exchangeable image file format）信息获取。图像拍摄时，无人机的GPS 信息和飞行姿态信息都被记录在图像的EXIF 中，EXIF 是专门为数码相机照片设定的，可以记录数码照片的属性信息和拍摄数据。通过专业的EXIF 信息编辑软件，例如MagicEXIF 等，可以很方便地获取图像的EXIF信息；利用第三方库也可以便利地实现EXIF 信息的批量读取和编辑，例如Python 的exifread 库等。

2）通过无人机飞行记录获取。本研究使用的DJI-Matrix100 无人机可以将飞行轨迹和飞行姿态等信息记录在飞行记录文件中，记录频率为10 条/s。也就是说，通过飞行记录文件可以获取每个0.1 s 节点处的GPS 坐标、飞机姿态、相机姿态、起飞高度、电池信息，以及此时间点是否摄影或摄像等信息。为了获取准确的时间间隔，本研究使用帧速率30 fps 的视频作为分析对象，每3 帧提取1 帧图像，这样相邻两帧图像的拍摄时间正好间隔0.1 s，一帧图像对应一条飞行记录，具体的获取流程见图3。

图3 通过飞行记录文件获取外部参数流程Fig.3 Process of obtaining external parameters from flight information files

2.3 矫正精确度

2.3.1 参照点的定位误差

图4为定位精度试验中使用的参照点位置示意图。

图4 定位精度试验中使用的参照点位置示意图Fig.4 Schematic diagram of reference point position in the positioning accuracy test

由于飞行高度误差等的影响，计算获得的参照点空间坐标会有一定的误差，为了研究误差程度及其对流速测量结果的影响，将现场用长卷尺量得的各参照点之间的距离（如图4）和定位计算得到的参照点之间距离进行对比，参照点距离误差情况如表1所示。

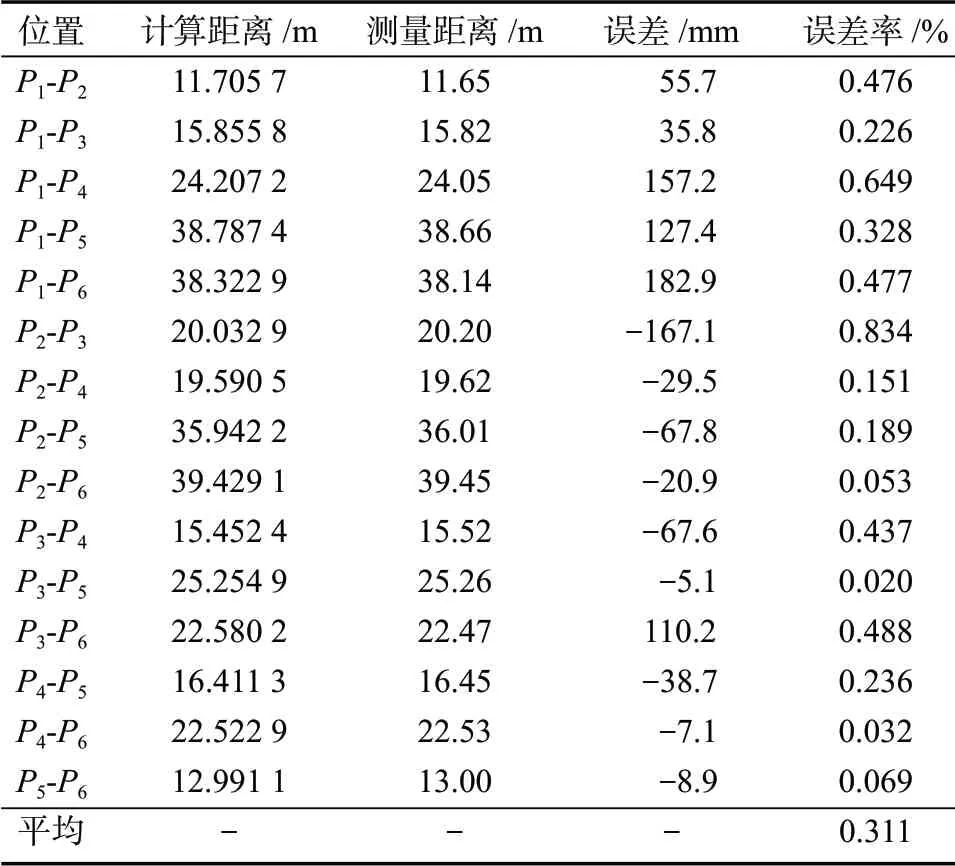
表1 参照点距离计算误差结果Table 1 Calculation error table of reference point distance

从表1可知，参照点距离计算的最大误差率为0.834%，平均误差为0.311%。影像测速的原理是根据示踪物在两张连续图像之间的移动距离和两图像的拍摄间隔时间来确定速度，在间隔时间固定的情况下，距离误差率会直接导致相同比例的流速误差率。由于水无常态，因此流速测量往往很难做到绝对的精准，通常要求单次测量误差在10%以内。因此，最大0.8%左右、平均0.3%左右的误差率完全可以满足流速测量的需要。

2.3.2 使用参照点时的图像矫正误差

本试验使用时长5 s 左右，帧速率30 fps 的视频，每3 帧提取1 帧，共提取51 帧图像作为分析对象，无人机飞行高度约17 m，矫正缩放系数n=180 pix/m，即每像素对应长度约5.55 mm。图像矫正的目的除了获取正射图像外，还应保证固定物体（参照点）在每帧图像上处于同样的像素位置，也就是说，参照点在每帧图像上的像素坐标偏差越小，则矫正的效果越好。本试验中矫正后各参照点在每帧图像上的像素坐标偏差情况如表2所示。

表2 图像矫正误差计算表Table 2 Calculation table of image correction error

根据矫正结果，在此次试验中x、y方向的极差平均为3.67, 2.33 像素，换算为长度则分别为20.4 ,12.9 mm。如果考虑结果的离散程度，全体平均差为0.65 像素，x、y方向的标准差分别为1.055, 0.541 像素，分别相当于5.86, 3.0 mm。这种程度的误差，在STIV（spatial-temporal image velocimetry）方法的应用上影响较小。

2.3.3 未使用参照点时的图像矫正误差

在不使用参照点的情况下，由于外部参数已知，可以直接根据相机的位置和姿态，利用数字图像处理技术对图像进行平移和三维旋转，获得正射影像。为了研究矫正误差的大小，分别用试验水渠河岸的固定区域和自然河道进行了测量，然后对比相邻的两帧图像中固定物体的偏移情况。图5选出了其中比较具代表性不使用参照点时矫正出现误差的影像。

图5 不使用参照点矫正图像时的误差特点Fig.5 Features of errors in image correction without reference points

图5中，图5a 出现误差是因为两图片之间存在平移；图5b 和5e 原因是两图片之间存在偏航角偏差（yaw 角误差）；图5c 和5d 出现误差的原因是两图片之间存在横滚角和俯仰角偏差（5c 为后图roll 角小，pitch 角大；5d 为后图roll 角大，pitch 角小）。

从图5可以发现，这种方法对于外部参数的准确度要求很高，而无人机的GPS 定位精度并不高，姿态角度也只精确到0.1°，这是导致连续的两张图像之间出现偏差的主要原因，这种偏差对影像测速有较大的不利影响，然而不同的图像测速方法对这种影响的敏感度也不一样，选择一种合适的图像分析方法有可能减少一部分矫正误差带来的影响。

3 图像分析方案选择

目前，河流表面图像测速的方法主要有大尺度粒子图像测速（LSPIV）和时空图像测速（STIV）两种。LSPIV 技术的原理很简单，在图像1（在时间t拍摄）中选择一个区域作为查询区域（interrogation area），同时在图像2（在时间t+Δt拍摄）上确定一个搜索区域（searching area）（如图6）。利用互相关算法找出查询区域在图像2 中的位置，进而得出查询区域在时间间隔Δt内移动的距离，就可以计算出移动速度。

图6 LSPIV 原理示意图Fig.6 Schematic diagram of LSPIV principle

STIV 首先选择合适的时间间隔Δt，采集M帧图像序列；然后在图像中沿待测水流的运动方向设置一组宽度为单像素、长度为L（约50~80）像素的测速线，将这些测速线按时间序列组合在一起，以L-t为直角坐标系合成一幅大小为L×M像素的时空图像。图7为STIV 原理示意图。

图7 STIV 原理示意图Fig.7 STIV schematic diagram

从图7可以看出，河流水面测速线构成的时空图像具有显著的纹理特征，表现为具有特定方向性的明暗条带。将纹理主要走向和纵坐标轴间的夹角φ定义为时空图像的纹理主方向，则tanφ=L/t，即该时间段的流速。

时空图像中的纹理线条，会呈现出特定的倾斜方向，并随机分布在图像的各个位置。图8为时空图像纹理倾斜度检测原理图。

图8 时空图像纹理倾斜度检测原理Fig.8 Principle of spatio-temporal image texture inclination detection

根据傅里叶变换幅度谱的自配准性质[13]，若原图像的长宽相等，不管这些倾斜的纹理线条的位置和分布如何，只要对它进行傅里叶变换获取其幅度谱，则这些倾斜纹理对幅度谱的贡献都会被集中地反映在通过幅度谱中心，且垂直于原纹理线条方向的直线上，如图8c。

如图8d 所示，以幅度谱的中心点为原点O建立极坐标系，以图像边长的一半，即N/2 作为搜索半径设置搜索线，以Δθ=0.1°为步距，0~180°作为搜索范围。统计搜索线上的幅度值F(r,θ)，即可按下式计算能量-角度分布：

能量峰值对应的角度即为所求的倾斜角度。在实际应用中，可以估计流速的大概范围，进而减少范围，提高算法效率。

在使用LSPIV 方法对图像序列中两幅相邻图像进行匹配时，图像矫正过程中的偏差会直接导致与偏差量相同数值的查询区域运动距离的计算错误，以至最终影响流速计算结果。而STIV 是根据时空图像（spatial-temporal image，STI）的纹理倾斜度测定一个时间段的流速，且STI 是由这个时间段内每一帧图像中提取一条检测线组合而成，其中相邻两帧图像之间的少许误差对STI 的整体纹理倾斜度几乎无影响。图9为图像矫正误差对时空图像纹理的影响示意图。

图9 图像矫正误差对时空图像(STI)纹理的影响示意图Fig.9 Effect of image correction error on spatio-temporal image texture

从图9可看出这一点，图中静止的参照点在STI中显示为一条竖直纹理，矫正误差导致这条竖直纹理出现了少量的不规则性，但是这种不规则性几乎不会对纹理主方向的判断造成影响，从这个角度来说，STIV 能更好地适应本研究所提出的图像矫正方法。

4 现场试验验证

为了验证这种图像矫正方法在现场试验中的适用性，分别在韩国安东河流试验中心急流试验河道和釜山市温泉川进行了现场验证试验。现场情况如图10 所示。其中，在安东河流试验中心的试验中，使用了泡沫作为示踪物，分别在图10a 所示的直线和曲线河道进行了影像采集。温泉川试验选在了上游的内院桥（）附近，由于是秋季，水面漂浮了一些树叶可以作为示踪物，因此没有使用人工示踪物。试验环境如表3所示。

图10 河流流速现场测定试验场地图Fig.10 Field test site for river velocity measurement

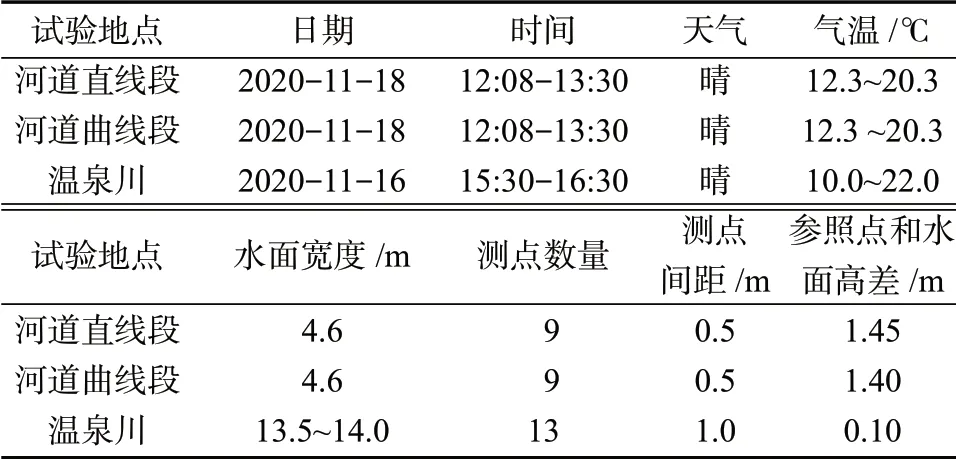
表3 河流流速现场测定试验环境Table 3 Test environment for river velocity measurement

本次试验中，为了对比结果的准确度，用声学多普勒流速仪FlowTracker 测量了相同位置各个测点的流速，与影像测速仪获得的流速进行对比，流速测量结果如表4和表5所示。

表4 模拟河道流速试验结果Table 4 Field experiment results of simulated river velocity measurementm/s

表6 自然河流流速试验结果Table 6 Field experiment results of natural river velocity measurement m/s

如果以多普勒流速仪的测量值作为参考真值，影像测速仪在使用和不使用参照点的情况下，试验水路直线段的平均流速测量误差分别为0.044 m/s（4.4%）和0.035 m/s（3.5%），曲线段的平均流速测量误差分别为0.008 m/s（0.8%）和0.044 m/s（4.6%），自然河道的测量中，平均流速测量误差分别为0.001 m/s（1.1%）和0.019 m/s（28.7%）。

可见，在试验河道，即使不使用参照点矫正图像，由于示踪物充足，也能获得较为准确的流速。然而，在示踪物较少的天然河道的试验中，如果不使用参照点的话，由于矫正偏差较大，因此，在示踪物密度较低的情况下，往往无法很好地捕捉到示踪物的轨迹，出现了大量异常值，而且流速测量的准确度也明显低于使用参照点的情况。

5 结论

利用数字图像分析技术的河流表面流速测定方法（SIV）是一种高效、安全、准确度高的非接触式流速测定方法。无人机作为一种新的视觉媒体设备，通过高空垂直摄影可获得良好的视觉影像，而且可以在很多车辆和人难以接近的区域使用。本研究利用无人机的优点，把用无人机拍摄的河流表面影像作为分析对象，开发出基于无人机图像的河流表面影像流速测定系统。

在对无人机拍摄的影像进行分析时，最大的问题是无人机自身的晃动，特别是大风等极端天气下，无人机很难稳定悬停，因而在摄像机和水面之间存在相对运动。在这种情况下拍摄的图像不宜直接作为分析对象使用，应先进行矫正。

本文开发出利用无人机飞行信息中记录的位置和姿态信息，对无人机拍摄的影像进行正射矫正的方法。在使用参照点的情况下，矫正后图像中，同样的固定物体在不同的图像中只存在最大2~5 像素的偏差，完全可以满足图像测速要求。而不使用参照点的情况下，由于无人机位置和姿态信息不准确，图像校正的精度较差，但是在示踪物丰富的试验河道测量中，仍然获得了比较精确的测量结果，可以满足水文测量的精度需求。即使在示踪物不充足的自然河流试验中，平均流速误差也仅为0.019 m/s。

未来将设法对现有的无人机影像测速技术进行优化，具体包括：1）结合现有的图像矫正方法，设法弥补无人机位置和姿态记录不够精确的问题，在不使用参照点的情况下，提高图像矫正精度；2）结合现有的STIV 算法，研究更高效且可以准确判断水流方向的图像测速技术。