基于等效刚度法的车体结构碰撞建模与参数优化

张敬科，朱 涛，雷 成，王小瑞，杨 冰，肖守讷，阳光武

(1.西南交通大学牵引动力国家重点实验室，成都 610031；2.郑州铁路职业技术学院河南省轨道交通智能安全工程技术研究中心，郑州 451460)

中空铝合金型材结构广泛应用于轨道交通车辆车体，是实现车体轻量化的重要途径之一[1]。由于铝合金挤压型材结构的特殊性，限制了有限元模型网格的大小，同时动车组车辆尺寸大、结构复杂、部件数量众多，如果采用全尺寸模型建立有限元模型，将会导致有限元模型网格数量庞大，计算机时大幅增加。因此，在整车有限元模型的基础上，对变形较小的客室区部分型材结构进行等效简化建模，降低有限元模型网格数量，提高整车碰撞计算效率，对缩短车体结构耐撞性设计周期具有重要意义。

为了提高列车碰撞仿真计算效率，Tang 等[2]提出了一种数据驱动的列车碰撞仿真建模方法，以现有的有限元模型计算结果为依据，通过机器学习算法预测未知碰撞速度下的碰撞响应，以在耐撞性设计初期提高效率，但在前期需要计算大量数据样本训练模型。另外，研究人员还基于多体系统动力学理论，将车体结构简化为质量块，通过一系列非线性弹簧-阻尼力元或者非线性曲线建立各质量块之间的连接关系，建立列车碰撞动力学模型，能够有效提高列车碰撞计算效率[3-6]。然而，多体系统动力学模型与有限元模型相比，不能清晰的反映碰撞能量波在列车上的传递，以及各级吸能结构的变形情况。研究表明：完整的列车车体结构有限元模型对于验证和评估列车的耐撞性能是必要的，然而，对整列车的有限元模型进行仿真计算时，所花费的时间是巨大的[7]。因此，在轨道车辆碰撞仿真分析中对车体结构等效简化建模是十分必要的。

等效模型因其能够一定程度上反映结构的静态和动态特性，又能大大减少模型的复杂性，提高计算效率，一直以来都是研究的热点。研究人员针对不同求解问题分别基于应变能等效均匀化[8-10]、最小应变能[11]、振动模态等效[12]和刚度等效[13]等多种理论对车体结构中挤压型材、中空钢夹层板形式桥面板、裂纹参数求解和材料硬度预测等进行等效计算，整体误差均满足工程要求。目前，等效模型在汽车碰撞仿真分析中有较多的应用，例如，Schäffer 等[14]利用从整体碰撞模型中获得的结构整体变形特征，将正面碰撞过程中承受弹性变形的结构区域以质量点代替，仅保留前端发生塑性大变形的结构，在确保计算精度的情况下，简化模型在Euro NCAP 偏移碰撞分析工况下的计算时间减少了大约92%。Liu[15]通过构建一种可以模拟多轴弯曲行为的二维旋转弹簧单元，对汽车底架中大长薄壁构件进行简化，建立了一个“全功能”简化车辆模型。通过对比验证，该模型能够正确预测和模拟斜碰撞过程中底盘的碰撞响应，且计算时间缩短了97%。但是，等效模型在轨道车辆碰撞仿真分析中鲜有应用，研究轨道车辆车体型材结构等效建模与碰撞仿真分析方法具有应用价值。

基于现有列车耐撞性标准要求[16]和碰撞数值模拟研究表明：同一类型编组列车在对撞工况下，列车发生塑性变形的区域主要集中在车钩、防爬吸能装置、车体端部等弱刚度吸能区域，车体生存空间区域基本处于弹性变形阶段，不参与能量吸收[17-24]。因此，本文以等效刚度法为指导思想，在保证等效前后抗弯刚度、质量相等前提下，给出了中空型材截面梁等效为实芯截面梁的等效参数的求解公式，并通过优化算法对弹性模量和泊松比参数进行了优化，通过对比分析梁的自由模态，以及简化车体与等效车体模型与刚性墙碰撞后的速度、加速度、界面力等碰撞响应结果，验证了等效模型在车体碰撞中应用的可行性与有效性。

1 车体等效参数计算及优化

基于等效刚度理论，结合铝合金焊接结构车体结构特点和多岛遗传优化算法，确定了铝合金中空型材结构等效为实芯截面结构等效参数计算方法，其实施流程如图1 所示。

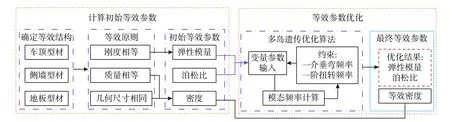
图1 结构等效参数计算及优化Fig.1 Calculation and optimization of structural equivalent parameters

1.1 车体等效区域型材剖分方法

根据欧洲耐撞性评估标准EN15227:2020[16]的要求，对于新设计的耐撞性车辆，当吸能区域的吸能单元完全压溃后，由结构形成的生存空间应保持完好，允许结构局部有一定的塑性变形和局部屈曲，但是在满足各工况下，乘客生存空间中的任意纵向5 m 长度的变化量不能超过50 mm，或塑性应变不能超过0.1，因此，车顶、侧墙和底架等结构构成的乘员区域的变形量相对于端部吸能区域的塑性大变形的变形量非常小，由其结构弹性变形或少量的局部塑性变形产生的能量与端部结构1 MJ 以上的吸能量相比可以忽略不计，可以认为该区域结构的型材处于弹性范围内。基于以上分析，可以对车体结构中乘员保护区域的车顶、侧墙和底架地板等结构型材在弹性范围内进行等效简化。

目前，轨道交通车辆车体结构大多采用大截面中空挤压铝型材焊接而成，为了对耐撞性车体中部非大变形乘员区域的挤压铝型材进行等效简化，需要对等效区域的型材结构进行剖分，以便于得到能够代表其力学性能的最小结构单元。如图2 所示，以车顶结构为例进行结构的剖分说明。图2 中：①为根据车体结构的截面确定车顶、侧墙、底架等结构的焊接形式，各部件的剖分部位；②和③为根据车顶与侧墙的焊接形式对车顶沿③中绿色箭头所示方向进行整体切割，并去掉车顶设备安装座型材结构，得到④中所示车顶型材结构；④为根据车顶型材结构特点，共分成3 个区域且各区域型材的截面形式相同；⑤为在④中车顶型材的基础上进一步剖分，由车顶型材结构可知，车顶是由若干小截面的中空型材插接拼焊而成，根据图中插接焊缝特点，沿焊缝方向继续切割，最终得到能够代表车顶型材力学性能的最小结构单元，如图2 中⑥所示。

图2 车顶中空挤压铝型材剖分方法Fig.2 Splitting method for hollow extruded aluminum profile of the roof

1.2 等效部件及局部结构简化

铝合金焊接车体由大型中空挤压铝合金型材焊接而成，其截面具有一定的对称性、重复性和厚度一致性。本论文对车顶、侧墙和底架枕梁内侧的地板挤压型材进行了等效建模。为了方便型材结构等效参数计算，对型材截面进行了一定简化，在1.1 节车顶剖分的基础上以车顶截面为例进行详细说明。

某铝合金焊接车体结构车顶截面和等效截面如图3 所示。图3 中双点虚线框中车顶为等厚度区域，厚度为hr1，两侧与侧墙连接部分厚度hr2＞hr1，为了方便等效参数计算，将两侧厚度简化为hr1。车顶等效截面模型与原模型具有相同的厚度(hr1)、宽度(Wr)、长度和曲线半径等几何尺寸。车体侧墙与底架和车顶连接部分型材厚度采用与车顶同样的简化方法，不再详细叙述。

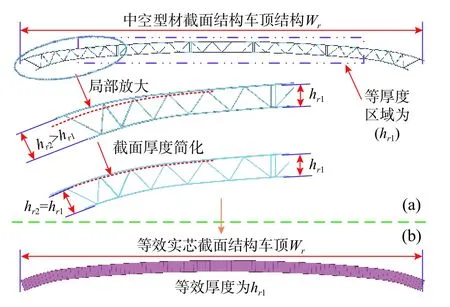
图3 中空挤压型材车顶截面及等效截面Fig.3 Hollow extruded roof section and equivalent section

1.3 等效原则

合理的等效原则是保证原模型与等效模型在静力学特性和动力学特性方面保持一致的关键。列车在运行过程中，车辆地板、侧墙、车顶等大型挤压型材，在载荷激励作用下以弯曲、扭转变形为主；为保证等效截面模型与中空截面模型在动力学特性上保持一致，应使两者抗弯刚度、转动惯量和质量相同。

1.3.1 代表性体积单元

研究结果表明：通过选取周期性结构的代表性体积单元，得到该结构的多向等效模量，建立其结构均质化模型，可以代替传统的完整结构精细化建模[25]。

由于中空型材一般具有对称性，因此，选取其代表性体积单元进行分析。以车顶型材为例，其代表性体积单元如图4 所示。图4 中：长度单位为mm；W为截面总宽度；h为截面厚度；Wi为型材空隙宽度；hj为型材空隙高度。将中空型材空心截面等效成实芯截面，等效时保持宽度和厚度不变，等效板截面宽度Wd=W，厚度hd=h。

图4 中空型材代表性体积单元截面Fig.4 Cross section of representative volume unit of hollow profile

1.3.2 简支梁抗弯刚度相等

车体底架在二系簧支撑下和车钩力作用下沿轨道运行，根据其受力特性可将其简化为简支梁模型[13,26]，如图5 所示。

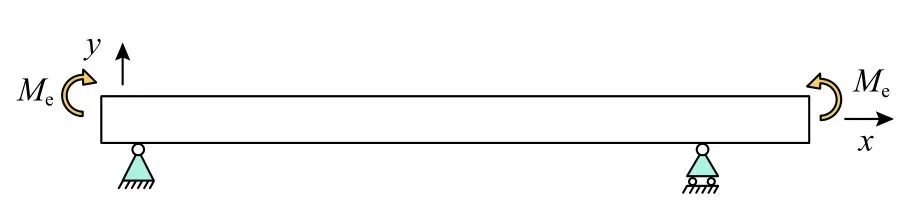
图5 单元截面等截面简支梁模型Fig.5 Simple supported beam model with constant cross section

简支梁长度为L，梁端部相对转角为 θ。假设该简支梁在受到梁端部力偶Me作用下材料仍处于线弹性范围，则梁中性层曲率表达式为：

由式(1)可得Me与 θ呈线性关系，且1/ρ=Me/EI，则Me在梁上的做功方程为：

由功能关系，可得梁内部存储的应变能U：

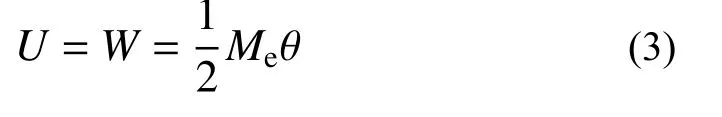
将1/ρ=M/EI代入式(3)可得：

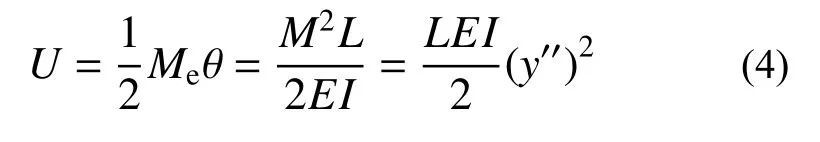
对于图4 所示的中空型材截面和实芯截面，设中空型材截面等效弯曲刚度为EI，实芯截面梁弯曲刚度为EdId。

令中空型材截面梁的弯曲应变能为U1，实芯截面梁弯曲应变能为U2，设两者差值为ε，可得：

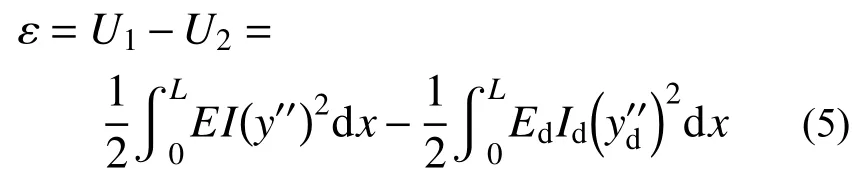
式中：y为型材截面梁的挠度；yd为实芯截面梁的挠度。

如果实芯截面梁和中空型材截面梁完全等效，则ε=0，代入式(5)即可求得等效截面梁的等效弯曲刚度。由材料力学简支梁挠度计算公式可得，对于同一种几何边界条件且沿长度方向截面尺寸不变化的梁，其挠度曲线函数形同[27]，对式(5)化简最终可得：

假定等效截面的宽度Wd与原截面的宽度W相等，可得：

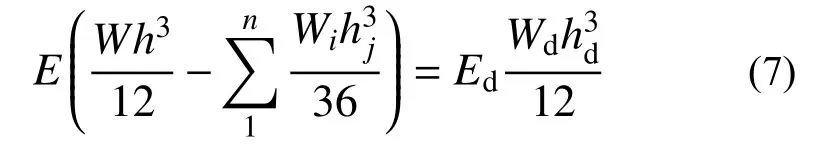
1.3.3 质量相等

等效后截面尺寸厚度h、长度L和宽度W不变，为保证等效前后的质量相等，由质量计算式(8)可得式(9)：

式中：A为截面面积；V为体积；ρ为等效前材料密度；ρd为等效后材料密度。

1.3.4 转动惯量相等

根据振动力学理论，在利用模态试验法测量结构件的质心和转动惯量时，根据待测件上测点的坐标测得测点的振动加速度，将测量结果作为已知，带入质心处动力学方程和质心与坐标原点的加速度关系方程即可以求解得到质心的坐标，同理，联立质心处振动角加速度动力学方程和质心处力矩平衡方程可以求解得到相对质心的转动惯量，即构件的转动惯量和构件的模态是紧密相关的[28]。若等效前后结构的振动模态频率误差在允许范围内，说明等效前后结构件的转动惯量是基本相同的，因此，本文并未对转动惯量参数具体约束。

1.4 初始等效参数计算

由式(7)和式(9)可得到等效实心截面结构材料的初始等效弹性模量和等效密度参数。但在以上公式推导过程中，未考虑弹性模量对扭转刚度的影响，以及泊松比对弯曲刚度和扭转刚度的影响，为了提高等效模型的计算精度，需要基于图1的流程对弹性模量和泊松比进行参数优化。等效过程中保持截面宽度和厚度、部件长度不变，则密度为定值不需要进行优化。

1.5 等效参数优化

为了提高等效结构的计算精度，以I-Sight 为平台建立了包含等效结构模态频率计算和参数优化的计算模型，如图6 所示。首先，给定弹性模量和泊松比的变化范围和初始值，调用ABAQUS进行模态频率计算，以实际结构与等效结构的一阶垂弯频率和一阶扭转频率的相对误差为优化目标，利用多岛遗传算法(Multi-Island Genetic Algorithm，简称MIGA)对变量进行分组实验设计优化，得到约束条件下最优等效参数，提高等效模型的精度。多岛遗传优化算法为I-Sight 平台集成模块，在此不详细描述。

图6 基于I-Sight 平台的等效参数优化模块Fig.6 Equivalent parameter optimization module based on I-Sight platform

2 等效模型有效性验证

2.1 车体结构的等效与对比

基于碰撞能量管理原则，将车体结构划分为客室区、司机室区和吸能区三部分，如图7(a)中所示。等效时，车体底架主承载结构(边梁、枕梁等)和司机室结构不变，将客室区的车顶型材、侧墙型材和底架枕梁内侧的地板型材进行等效处理(图7(b)中所示结构)；等效后的车体截面轮廓如图7(c)中所示，中空截面等效为实芯截面。等效部分不改变结构的厚度、宽度、长度和曲线半径等几何尺寸，车体结构等效前后的区别主要体现在以下两点：

1)等效前后车顶、侧墙和底架地板的截面不同，等效前为中空截面，等效后为实芯截面，如图7(c)中所示。

图7 车体结构等效区域Fig.7 Equivalent area of car body structure

2)连接部位的连接形式不同，例如图8 中所示部分连接结构，等效前，车顶、侧墙和地板分别通过型材结构与端墙型材、底架边梁连接；等效后，车顶、侧墙和地板分别通过等效实芯板与端墙边梁、底架边梁连接。

图8 等效前后车体结构连接部位的区别Fig.8 The difference between the connecting parts of the equivalent front and rear car body structure

等效后的车体包含原车体结构的主要结构形式，等效部分的材料参数如表1 所示，未等效部分为实际材料参数和几何结构参数，主要为铝合金材料5083-O 和6A01-T5，弹性参数如表1 所示。

表1 材料实际参数和等效参数Table 1 Actual parameters and equivalent parameters of materials

文中采用LS-Dyna 中的Belytschko-Tsay 壳单元对车体模型进行离散，司机室及车体端部吸能区域单元尺寸为25 mm，中部乘员区域等非大变形区域单元尺寸为50 mm，非等效区域及等效前的车体结构的材料模型为3 号双段线性弹塑性本构模型，其输入应力-应变曲线如图9 和图10 所示，屈服强度分别为125 MPa 和205 MPa，失效应变为0.18，在低速碰撞工况下未考虑材料的应变率效应。

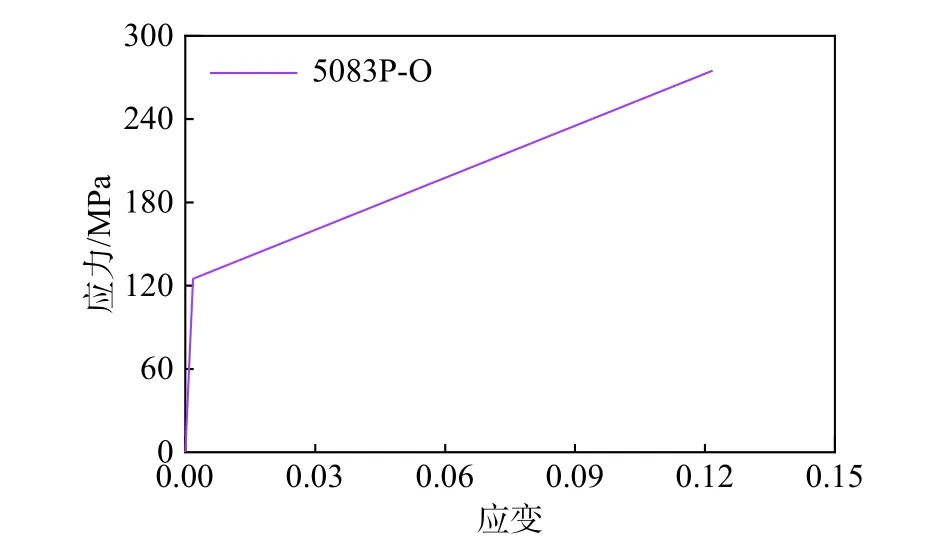
图9 材料5083P-O 应力-应变曲线Fig.9 Stress-strain curve of material 5083P-O

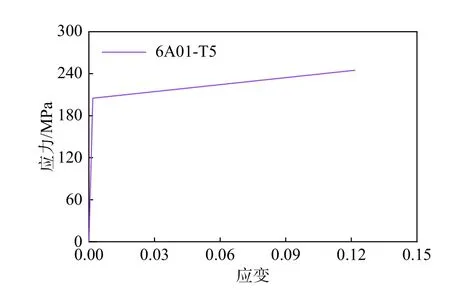
图10 材料6A01-T5 应力-应变曲线Fig.10 Stress-strain curve of material 6A01-T5

由1.1 节分析可知，车体等效区域本身处于线弹性或者局部塑性变形状态，基于此，等效区域在等效后只考虑了材料的弹性参数，未考虑其塑性参数和应变率效应，其单元类型与原模型的单元类型一致。

2.2 车体结构的等效与对比

根据《铁道车辆强度设计及试验规范》(TB/T 1335-96)[29]，评价车体刚度的两个主要指标是底架中梁挠度、一阶垂弯频率和一阶扭转频率。车辆在碰撞工况下，车体侧墙、车顶和底架地板以动态特性为主，因此，着重考察等效模型和原模型在一阶垂弯和一阶扭转等特性指标的差别。

以某城轨车辆为例(车体模型如图7(a)中所示)，基于车体等效参数计算式(7)和式(9)得到等效弹性模量和等效密度的初始值。根据初始值计算结果和参数实际取值范围，等效弹性模量的优化范围为计算初始值的30%范围内，泊松比的优化范围为0.1～0.5，利用优化方法对等效弹性模量和泊松比进行优化，得到车顶、侧墙和地板代表性体积单元等效模型的等效参数如表1 所示。最优参数下的等效模型和原模型相同振型的自由模态频率计算结果如表2 所示。从计算结果可知，单个等效模型和原模型的一阶垂弯和一阶扭转模态频率误差均在10%以内，整车车体结构一阶垂弯和一阶扭转模态频率误差分别为2.19%和4.21%，其振型图如图11 所示，等效模型能够较好的反映原模型的动态特性。

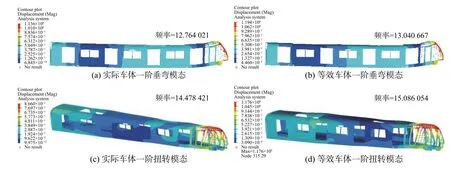
图11 等效前后车体结构一阶垂弯和扭转振型图Fig.11 The first-order vertical bending and torsional vibration mode of the equivalent front and rear car body structure

表2 材料实际参数和等效参数Table 2 Actual parameters and equivalent parameters of materials

图12 给出了等效前后车顶、侧墙和端墙之间的连接关系。结合图8 可以看出，等效后车顶和侧墙与端墙的连接由原来的型材双侧连接变成了单个板材的连接，另外在等效过程中将车顶设备安装座进行了简化，同时侧墙与门柱之间的型材双侧连接同样变成了单个板材连接，因此，在等效后车顶、侧墙部件的连接约束相对较弱，以及对各部件截面尺寸进行了一定的简化。另外，根据表1 中等效前后参数可知，等效后材料的泊松比变大，研究表明：泊松比参数对不同厚度的板壳的振型和模态频率影响是显著且复杂的[30-31]，随着泊松比的增大使振动频率增大，以上原因共同导致了等效前后车体整体振型和频率有一定的差异。

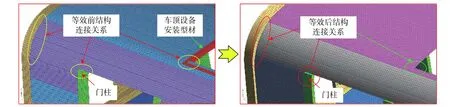
图12 等效前后车顶与侧墙和端墙的连接关系Fig.12 The connection relationship between the roof,the side wall and the end wall in the equivalent front and rear

3 验证碰撞响应特性对比分析

3.1 碰撞工况及边界条件

选取车辆以15 km/h 撞击刚性墙工况为研究对象。相同碰撞工况下，对比分析等效实心截面板和中空型材截面板构成的车辆碰撞过程中的速度、加速度、能量和客室生存空间变化情况，以验证等效模型的有效性。碰撞场景如图13 所示，原模型和等效模型碰撞场景相同。

图13 车辆碰撞工况Fig.13 Vehicle collision conditions

3.2 结果对比分析

仿真计算在有限元软件LS_Dyna 中完成，经过仿真计算得到车体的速度、加速度、压缩位移、能量等碰撞响应，并分别对比分析。

碰撞过程中两种模型车体结构的速度-时间对比曲线如图14 所示。由图14 可以看出，等效实芯截面板结构车体的速度变化曲线和中空型材截面板结构车体的速度变化曲线基本重合，车体从初速15 km/h 逐渐减速，在0.097 s 左右车体速度减至0。由于车体为弹塑性材料，碰撞过程中有一部分动能转化为弹性势能，当车体速度为0 时，弹性势能迅速释放，此时，车体反向加速，等效车体反向加速后的均值速度为-3.32 km/h(负号表示与原方向相反)，实际结构车体反向加速后的均值速度为-3.02 km/h，均值速度误差为9.88%，满足工程误差10%的要求，等效结构车体可以较好地反映碰撞过程中车体速度变化特性。

图14 碰撞过程中车体速度变化曲线Fig.14 The speed change curve of the vehicle body during the collision

加速度和界面力反映了车体在撞击过程中的剧烈程度。图15 和图16 为车辆与刚性墙碰撞过程中车体加速度和界面力变化曲线。对比加速度曲线可以发现，虽然曲线有一定差异，但是整体趋势是一致的，等效模型能够较好的反映加速度峰值和最大平均加速度，最大峰值加速度误差为0.52%，最大平均加速度误差为4.30%。从图16中界面力曲线可以发现，两种模型界面力曲线基本重合，加载阶段和卸载阶段具有较好的一致性。0 s～0.038 s 为车体端部吸能装置与刚性墙单独作用阶段；0.038 s～0.097 s 为吸能装置和司机室结构共同与刚性墙作用阶段，界面力增加；0.097 s后车体存储的弹性势能释放，车体反向加速，逐渐与刚性墙分离，界面力减小至0，碰撞过程中最大界面力误差为0.60%。

图15 碰撞过程中车体加速度变化曲线Fig.15 The acceleration curve of the vehicle body during the collision

图16 碰撞过程中界面力变化曲线Fig.16 The interface force change curve during the collision

整个碰撞过程中能量变化曲线如图17 所示。由图17 可以看出，等效实芯截面板结构车辆能量变化曲线和中空型材截面板结构车辆能量变化曲线基本重合。0.16 s 碰撞结束时，总吸能量(内能)误差为0.18%，实际结构车体剩余动能18.23 kJ；等效结构车体剩余动能20.58 kJ，误差为12%。由于剩余动能较小，在剩余动能差值2.35 kJ 时，误差略大于10%；但根据耐撞性校核标准要求，能量吸收量为主要考核指标，动能误差对车体结构耐撞性评价影响较小。因此，等效结构车辆可以用来验证车辆耐撞性设计性能。

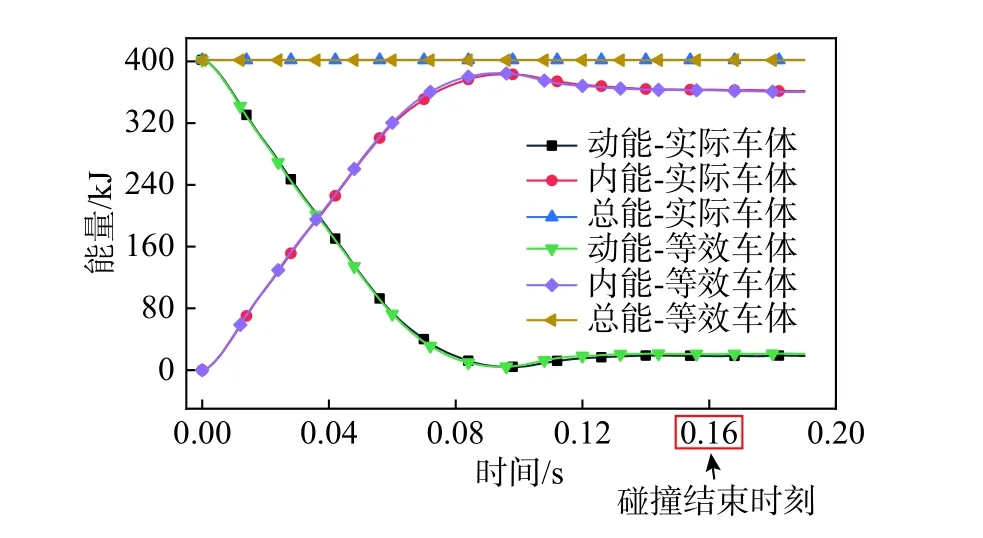
图17 碰撞过程中车辆能量变化曲线Fig.17 Vehicle energy change curve during the collision

图18 和图19 为碰撞过程中司机室生存空间纵向长度变化量、乘客区生存空间纵向长度变化量的变化曲线。从图18 和图19 中曲线可以看出，等效模型和实际模型的生存空间的纵向长度变化量的变化趋势一致，司机室生存空间纵向长度变化量最大值误差为6.63%，乘客区生存空间纵向长度变化量最大值误差为9.07%，等效车体结构能够较为准确的反映碰撞过程中车体结构生存空间的变化，为车体结构耐撞性校核提供依据。

图18 碰撞过程司机室生存空间纵向长度变化量-时间曲线Fig.18 Changes in the longitudinal length of the living space in the cab area during the collision

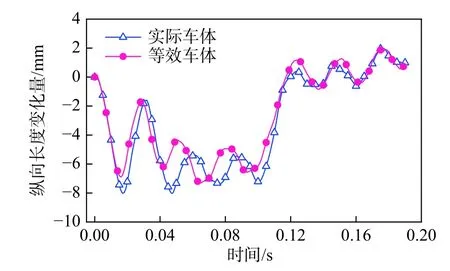
图19 碰撞过程乘客区生存空间纵向长度变化量-时间曲线Fig.19 Changes in the longitudinal length of the living space in the passenger area during the collision

吸能区域作为耐撞性车体结构中主要的吸能区域，其纵向变形量的大小反映了其吸能量的大小，应力分布一定程度上体现了碰撞过程中撞击力的传递路径，因此，吸能区域的变形模式、变形量和应力分布体现了等效区域对车体结构碰撞响应的影响。等效前后车辆模型在碰撞过程中吸能区域纵向压缩位移变化量曲线、端部变形模式和碰撞过程中关键节点的应力分布如图20、图21和图22 所示。等效模型较好的反映了原车辆结构在碰撞过程中吸能区域纵向压缩位移变化量的大小和变化趋势，最大纵向压缩位移变化量误差为3.38%。碰撞结束时，等效前后车体前端吸能区(吸能结构和司机室结构)变形模式基本一致。从碰撞过程中司机室端部结构的应力云图可以看出，在整个碰撞过程中，等效前后端部结构的应力分布基本一致，图22 中所示节点的最大应力的最大误差为9.37%。因此，等效区域结构能够较好地反映车体结构碰撞过程中的撞击力传递路径和端部大变形区域的塑性变形。

图20 碰撞过程中吸能区纵向长度变化量-时间曲线Fig.20 The change in the longitudinal length of the energy absorption zone during the collision

图21 型材车体(上)和等效车体(下)端部变形Fig.21 End deformation of the profile car body (top) and equivalent car body (bottom)

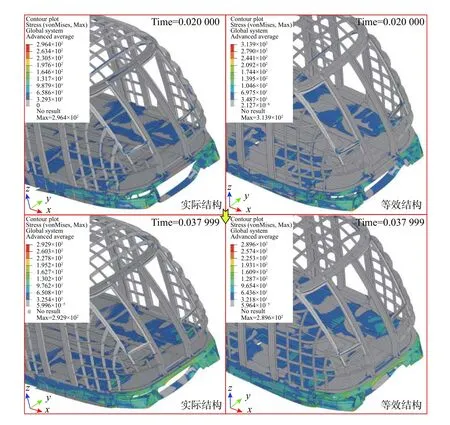
图22 碰撞过程中型材车体(上)和等效车体(下)端部变形区域应力云图Fig.22 Stress contour plot of the deformation area of the profile car body (top) and the equivalent car body (bottom) during the collision

由图18～图20 中纵向压缩位移变量曲线和表2中模态频率结果可以看出，等效模型的纵向压缩位移变化量(绝对值)略小于原结构车体纵向压缩位移变化量，即等效模型车体整体刚度略大于原结构车体整体刚度。因此，图16 中等效模型撞击刚性墙的界面力最大值略大于原结构车体撞击刚性墙的界面力。

图23 和表3 统计了等效前后车体结构在相同单元大小时的单元数量和相同硬件设备下CPU 计算时间。可以看出，在单元大小相同时，车顶、侧墙和地板在等效后有限元模型单元数量比原模型单元数量减少了62.01%，整个车体结构在等效后有限元模型单元数量比原模型单元数量减少了38.91%；在相同硬件设备和计算步长下，CPU 计算耗时缩短了27.63%，等效模型大大降低了有限元模型的单元数量，有效的提高了计算效率。

图23 车体碰撞计算耗时Fig.23 Calculation time of vehicle body collision

表3 等效前后单元数量和计算时间对比分析Table 3 Comparison and analysis of the number of elements and calculation time before and after equivalence

4 结论

本文基于等效刚度法建立了中空型材的等效模型，并利用多岛遗传优化算法对等效参数进行了优化，通过对等效模型的自由模态计算分析以及两种车体碰撞响应的对比分析得出以下结论：

(1)基于车体结构碰撞模型建模和等效参数优化方法，对车体结构中小变形区域的客室区型材结构进行等效建模，得到的等效模型能较好的反映实际结构的动态特性，车顶、侧墙和底架地板的代表性体积单元等效前后的一阶垂弯和一阶扭转频率相对误差均小于10%，整车车体结构等效前后的一阶垂弯和一阶扭转频率相对误差分别为2.19%和4.21%。

(2)车体等效模型较好地反映实际结构车辆的碰撞响应特性：车体等效模型相较于原模型碰撞界面力最大值误差为0.60%，最大平均加速度误差为4.30%，最大吸能量误差为0.18%；客室区生存空间纵向压缩位移变化量最大值、司机室区生存空间纵向压缩位移变化量最大值和吸能区纵向压缩位移变化量最大值误差分别为9.07%、6.63%和3.38%，主要安全性考核指标误差均满足工程误差要求。

(3)车体碰撞等效模型建模和参数优化方法提高了列车碰撞有限元分析的建模效率，降低了模型的单元数量，提高了仿真计算效率；在相同的单元大小时，等效后车体有限元模型单元数量减少38.91%，车顶、侧墙和地板部分的有限元模型单元数量减少62.01%；相同计算时间步长和硬件条件下，CPU 计算效率提高27.63%。

车体碰撞等效模型建模和参数优化方法，有助于在提高列车碰撞有限元计算效率的同时，用于对列车撞击力流传递、碰撞能量流动规律、端部各级吸能结构的变形模式和失效模式，以及碰撞响应变化规律的研究，对提高车体结构的耐撞性设计具有重要的理论和工程运用价值。