基于柔性管缆运动监测数据的位移计算方法

赵晨宇，罗晓兰，张 涛，刘军鹏

(中国石油大学(北京) 机械与储运工程学院， 北京102249)

柔性管缆是连接水下油气开采设备与水上浮式平台的重要设备，有顺应性强、安装和回收成本低等诸多优点，在深海油气生产中获得广泛应用。但是，由于柔性管缆长期受到风、浪、流载荷和船体往复摆动的挤压作用，非常容易发生过度弯曲和疲劳破坏。为此，必须通过实时监测的柔性管缆加速度运动数据，获得柔性管缆的瞬时位移，为柔性管缆弯曲强度和疲劳强度计算提供理论依据。

通过实时监测的柔性管缆加速度运动数据，求取瞬时运动姿态角，最终获得其瞬时位移的常用方法主要有欧拉角法、方向余弦法和四元数算法。

1) 欧拉角法。

用1组欧拉角来描述动态坐标系与固定坐标系之间的关系。该方法需要求解3个姿态角的微分方程。姿态角矩阵不需要正交化，但需用三角函数计算，工作量大[1]。当监测对象的俯仰角达到90°时，方程会出现奇异现象，不能进行全姿态角求解，应用有一定的局限性。淡鹏等针对火箭大角度运动下的姿态角计算问题，应用欧拉角法对实际案例进行了探讨和分析[2]。该方法对火箭姿态角解算和卫星姿态分析有一定的借鉴意义，但当火箭姿态角变化较大时，其计算结果存有较大误差。夏喜旺等研究了飞行器大姿态角的计算问题，推荐采用四元数法来描述飞行姿态角，以避免欧拉角法存在的奇异现象[3]。

2) 方向余弦法。

通过定点旋转的相应2个坐标之间的夹角余弦来表示姿态角矩阵。该方法可用于任意姿态角的计算，但计算量大，工程上并不实用。李连仲等推导了方向余弦矩阵的更新递推公式，通过仿真对其递推公式进行验证，研究并提升其公式精度[4]，可满足捷联惯导系统应用中的精度要求。刘恒春提出用三角函数法求解捷联惯导系统中的方向余弦矩阵，计算结果表明此方法精度高，但其计算过程颇为复杂[5]。刘瑞华提出新的3阶最小参数法来解算方向余弦矩阵微分方程，结果表明其计算精度与经典的3阶毕卡迭代数值计算方法差不多，但姿态角解算的响应速度即实时性显著提高[6]。

3) 四元数法(又称四参数法)。

通过建立的4个微分方程求解四维空间向量。运用四元数法求解姿态角，具有精度高、计算量小、可避免奇异性的优点，是目前计算姿态角的常用方法之一。四元数法需通过传感器陀螺仪输出柔性管缆运动时的角速率数据，运用四元数角速率法进行姿态更新。黄昊等针对陀螺仪角速率的姿态算法进行研究，理论上推导了几种航姿算法的误差表达式，计算结果表明四元数法和4阶Runge-Kutta法相结合是处理该问题的有效算法[7]。史凯等采用四元数法和4阶Runge-Kutta法研究炮弹姿态，进行仿真平台模拟和样机实际试验，证明该算法可推广工程应用[8]。许毛跃等解算姿态角时，发现计算步长对使用4阶Runge-Kutta法求解四元数微分方程时的计算误差有较大影响[9]。王德春等提出了Adams预测-校正-改进算法，提高了捷联惯导系统的姿态角解算精度[10-11]。

吴简彤等对比分析了四元数法、欧拉角法、方向余弦法[12]，研究结果表明：运用四元数法进行姿态角解算性能最佳，实用性更强。因而可用于柔性管缆姿态角的解算，而欧拉角法与方向余弦法因其计算量大、方程会出现奇异现象、公式复杂的问题，均不适用于求解姿态角。

本文将利用柔性管缆的实时监测数据，运用四元数法和4阶Runge-Kutta法进行姿态角的计算，并应用MATLAB软件，最终获得柔性管缆的实时位移数据。为此，柔性管缆实时监测系统是对实时位移求解精度具有重要的作用。

1 监测系统简介

1.1 监测总体方案

柔性管缆监测系统由管缆运动记录仪及夹具2个部分组成。此监测装置安装在防弯器下方1～2 m区域内的柔性管缆上，如图1所示。该区域为高应力或高疲劳损伤的部位，可捕获最大的加速度监测数据。

图1 监测系统布局示意

1.2 监测模块说明及测量数据

1.2.1 检测模块说明

监测系统的测量单元采用EPSON公司的G354传感器(如图2)，此传感器是1个6自由度惯性测量单元，包括三轴加速度计和三轴陀螺仪。其中，三轴加速度计记录监测点的三轴线性加速度数据，三轴陀螺仪记录监测点的角速率数据，监测数据实时存储在大容量SD卡中，定期提取记录仪存储的数据。监测模块采用高聚能锂电池组供电，可满足6个月连续工作的要求。

图2 G354传感器

1.2.2 测量数据及处理

监测模块获得的三轴线性加速度数据包括哥氏加速度、重力加速度和运动加速度，而柔性管缆的运动情况只与运动加速度有关，所以哥氏加速度与重力加速度作为加速度数据中的污染项，需被剔除。鉴于哥式加速度过小，可直接忽略。为剔除重力加速度，需要在加速度计水平和倾斜2种状态下分析计算。

1) 加速度计水平状态。

当传感器静止时，加速度计处于水平状态，如图3所示。此时，X0、Y0方向的重力加速度分量为0，而Z0轴方向的重力分量为g。

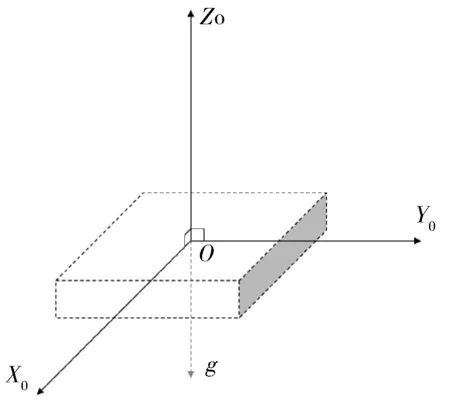
图3 三轴加速度计处于水平状态

2) 加速度计倾斜状态。

当加速度计随柔性管缆摇摆，处于倾斜状态时。此时，加速度计各轴与Z0轴存在一定的夹角，动坐标系OX1Y1Z1各轴与定坐标系OX0Y0Z0对应各轴的夹角为φ、θ、ψ，如图4所示。加速度计各轴在动坐标系内都有重力加速度的分量。

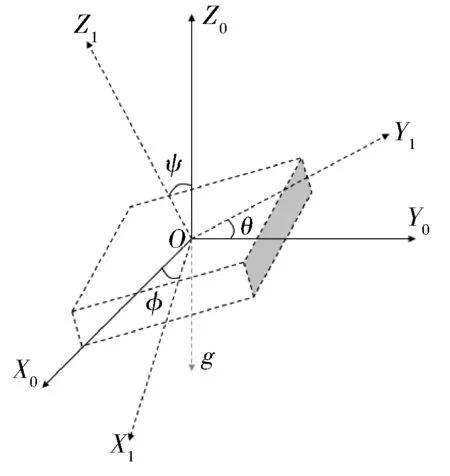
图4 三轴加速度计处于倾斜状态

要剔除动坐标系内各轴的重力加速度分量，需结合监测模块中三轴陀螺仪输出的角速率数据，计算任意时刻动坐标系各轴相对于定坐标系各轴的夹角，通过夹角确定各轴的重力加速度分量。为此，通过四元数微分方程及4阶Runge-Kutta法对三轴角速率处理，以对柔性管缆任意时刻的姿态角进行求解。

2 柔性管缆姿态角的求解

2.1 四元数表示坐标变换

四元数的数学表达式为：

(1)

四元数能便捷地描述刚体的角运动，通过旋转运算来实现这种转动关系。针对图4，OX0Y0Z0在经过旋转变换后，得到新坐标系OX1Y1Z1，其旋转运算表达式为：

(2)

(3)

(4)

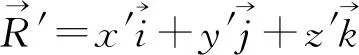
(5)

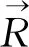
将式(1)和式(3)～(5)代入式(2)，进行变换，并用矩阵的型式表达，则有：

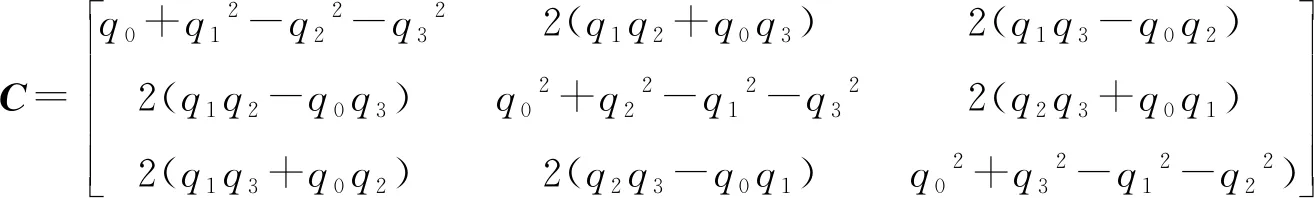
(6)

坐标变换系数决定着动坐标系相对于定坐标系的位置，系数矩阵C实质上就是姿态角矩阵，经姿态角矩阵可计算运动状态的姿态角，即，将矩阵式(6)简化为：

(7)

为了求解式(6)矩阵中的四元数值q0、q1、q2、q3，需建立四元数微分方程并确定四元数的初值，再应用4阶Runge-Kutta算法对四元数进行迭代，计算出任意时刻的四元数值。

2.2 四元数微分方程的建立

四元数微分方程一般用单位四元数来推导，四元数描述了刚体的定点转动，单位四元数的表达式[13-14]为：

(8)

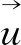
对式(8)进行求导，并将α的求导值用角速率ω表示，得到3个任意动坐标的角速率矩阵为：

(9)

式中：ωx为任意动坐标系中X轴的角速率；ωy为任意动坐标系中Y轴的角速率；ωz为任意动坐标系中Z轴的角速率。

由式(9)看出，四元数法在进行姿态角解算时，仅需解4个一阶微分方程，运算量显著减少。

2.3 四元数初值确定

四元数的初始值可看作是1个初始对准的过程。图4所示，设三向定坐标分别按照角度ψ、θ、φ转动3次后的四元数形式[15-16]为：

(10)

(11)

(12)

将Q1，Q2，Q3连乘得到Q，并用矩阵表达，有：

(13)

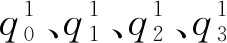
当ψ=0，θ=0，φ=0时，即初始时动坐标系与定坐标系重合，把初始夹角代入式(13)，求得此时的四元数初值为：

(14)

2.4 四元数微分方程的求解

Runge-Kutta法是一种精度较高的单步长算法，在工程中广泛使用。对于四元数微分方程式(9)，其4阶Runge-Kutta法表达式为：

(15)

式中：q为四元数向量；k为斜率；h为程序迭代的步长。

通过4阶Runge-Kutta法可解算出四元数微分方程，由四元数初始值开始逐点计算，陀螺仪测得的三轴角速率ωx、ωy、ωz作为输入条件，可计算出对应的任意时刻的四元数值，最终求解出式(7)的姿态角矩阵。

2.5 姿态角的求解

为了将式(7)姿态角矩阵的值转化成任意时刻的姿态角，需建立动坐标系的旋转矩阵，如图5所示，初始时动、定坐标系相互重合，然后将z轴固定,x轴与y轴转动ψ角，得动坐标系OX1Y1Z1；再将y轴固定,x轴与z轴转动θ角，得动坐标系OX2Y2Z2；最后，将x轴固定,y轴与z轴转动φ角，动坐标系在空间中到达位置OX3Y3Z3。

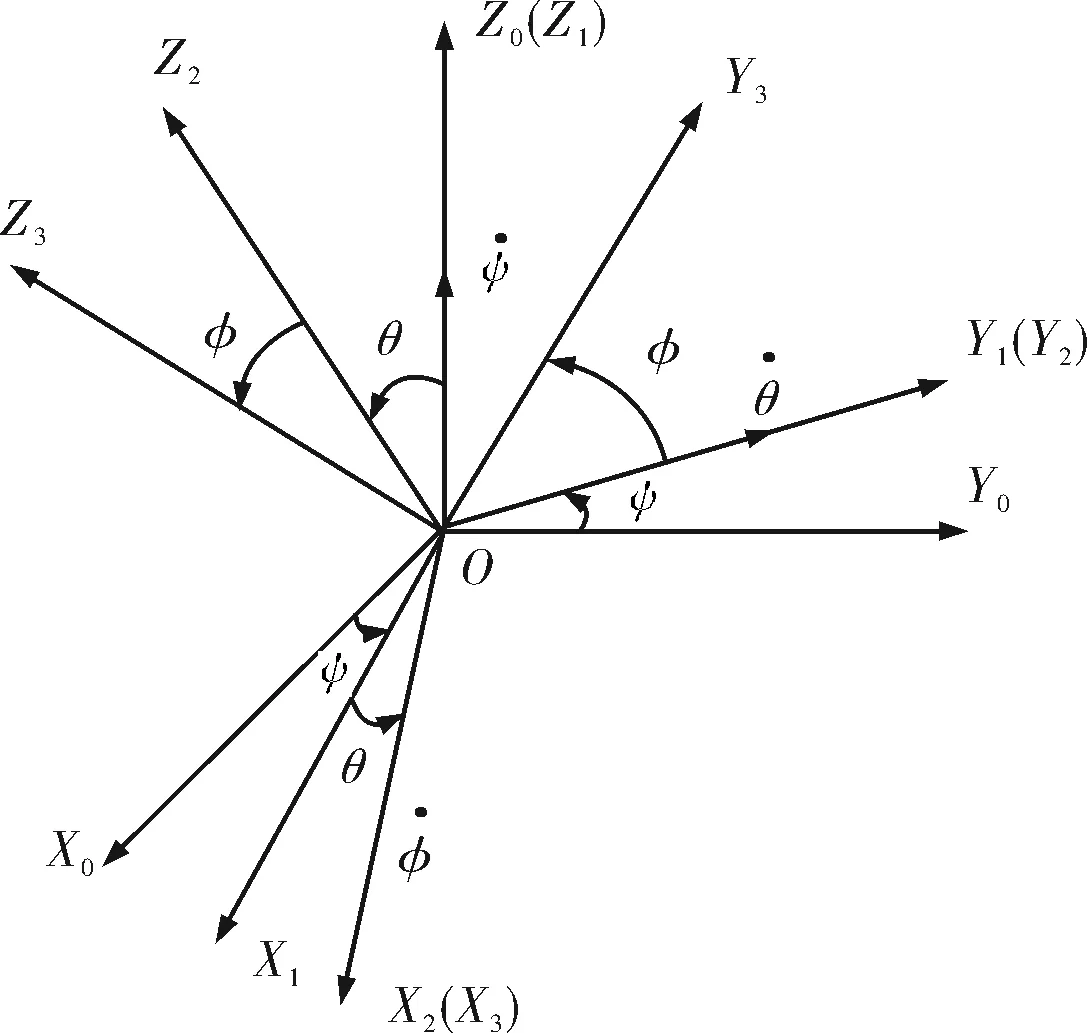
图5 三次转动结果

三次转动后的坐标系矩阵为：

(16)

从式(16)可以看出，转动后的坐标系矩阵最终形式不仅取决于转动次序，还取决于每次单独转动角的大小。四元数旋转矩阵与动坐标系旋转矩阵数学含义相等，四元数旋转矩阵转动向量是四元素，而坐标系旋转矩阵转动的向量是对应的坐标轴，因此，四元数旋转矩阵与坐标系旋转矩阵是等效的，则：

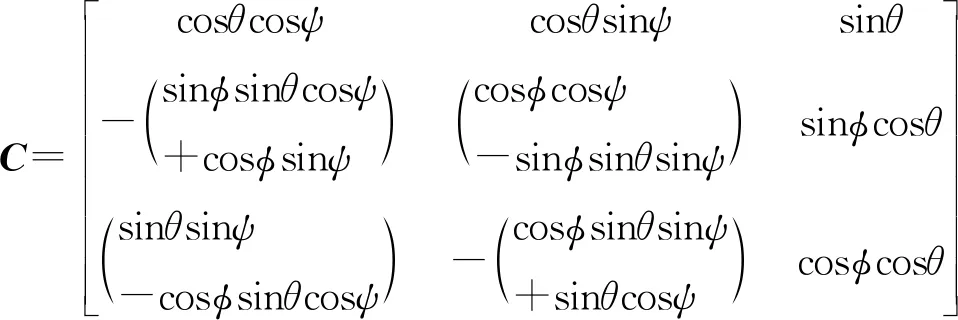
(17)

由式(7)和(17)得：

(18)

将四元数值代入四元数旋转矩阵，则可求得解算姿态角所需C21、C11、C31、C32、C33各元素的值，可由式(19)求得。

(19)

应用MATLAB软件将上述推导公式编程后，可完成对应时刻的四元数值及姿态角的求解。

3 柔性管缆位移数据求解

3.1 运动加速度求解

监测模块上测得的加速度关系式为：

(20)

重力加速度在动坐标系中的表达式为：

(21)

式中：Ax、Ay、Az分别为加速度计x、y、z三轴的读数；ax、ay、az分别为动坐标x、y、z三轴运动加速度的分量；gx、gy、gz分别为动坐标x、y、z三轴重力加速度的分量。

通过求解出的式(18)姿态角数据，可以求解重力加速度在三轴上的分量，并在监测模块获得的线性加速度数据中将其剔除。

3.2 监测点位移求解

利用剔除后的动坐标系的加速度ax、ay、az，应用FFT频域计算位移，先将运动加速度的时域信号转换到频域。然后根据傅立叶变换的性质，经过频域的积分和滤波后，通过傅里叶逆变换返回时域，此时得到的数组即为时域数组积分的结果。时域和频域中信号之间的对应关系可用离散傅里叶变换实现，对应关系为：

(22)

(23)

式中：a(n)为加速度信号；X(k)为a(n)的频谱；N为采样数据量；n、k均为非负整数。

对信号做离散化处理，并通过傅里叶变换，则有：

(24)

(25)

式中：v(n)、d(n)分别为速度信号和位移信号的离散化表示;ωk=2πkΔf，Δf=Fs/N,为频率分辨率。

根据上述算法，并参考王济[17]在频域中对振动加速度信号的处理，设计具体计算程序，应用MATLAB软件计算得出柔性管缆位移结果，为柔性管缆弯曲强度和疲劳强度计算提供一定理论依据。

4 仿真结果

通过MATLAB软件对上述公式进行编程计算，可得以下计算结果。图6为姿态角随时间的变化曲线。

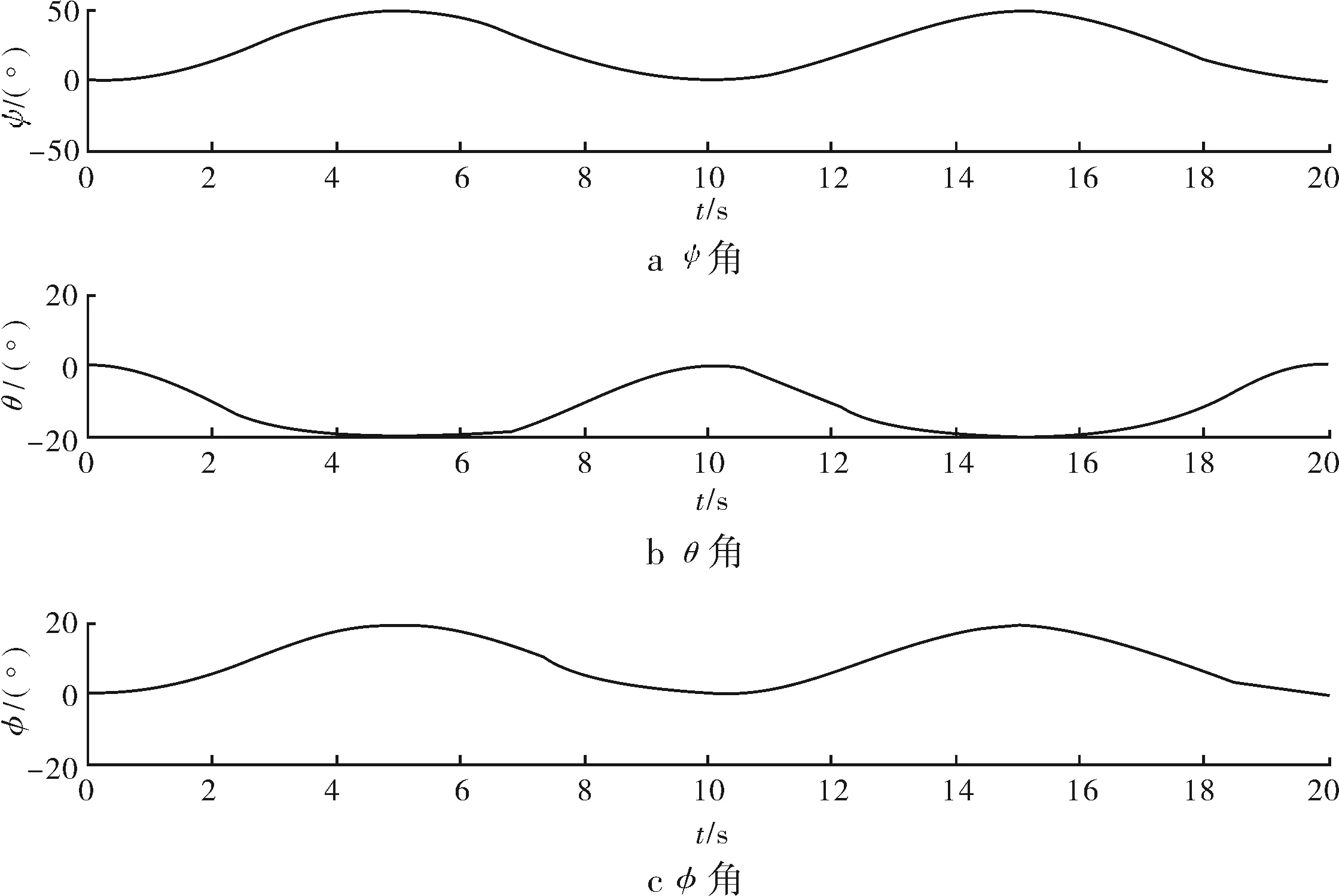
图6 姿态角信号

图7为重力加速度分量随时间的变化曲线。

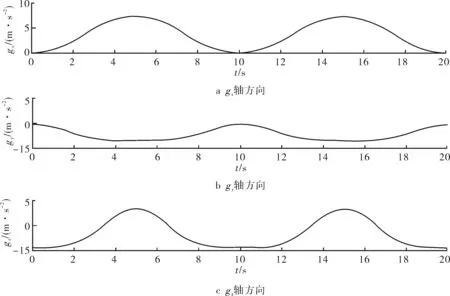
图7 重力加速度分量信号

图8为剔除加速度计中的重力加速度分量后，运动加速度随时间的变化曲线。

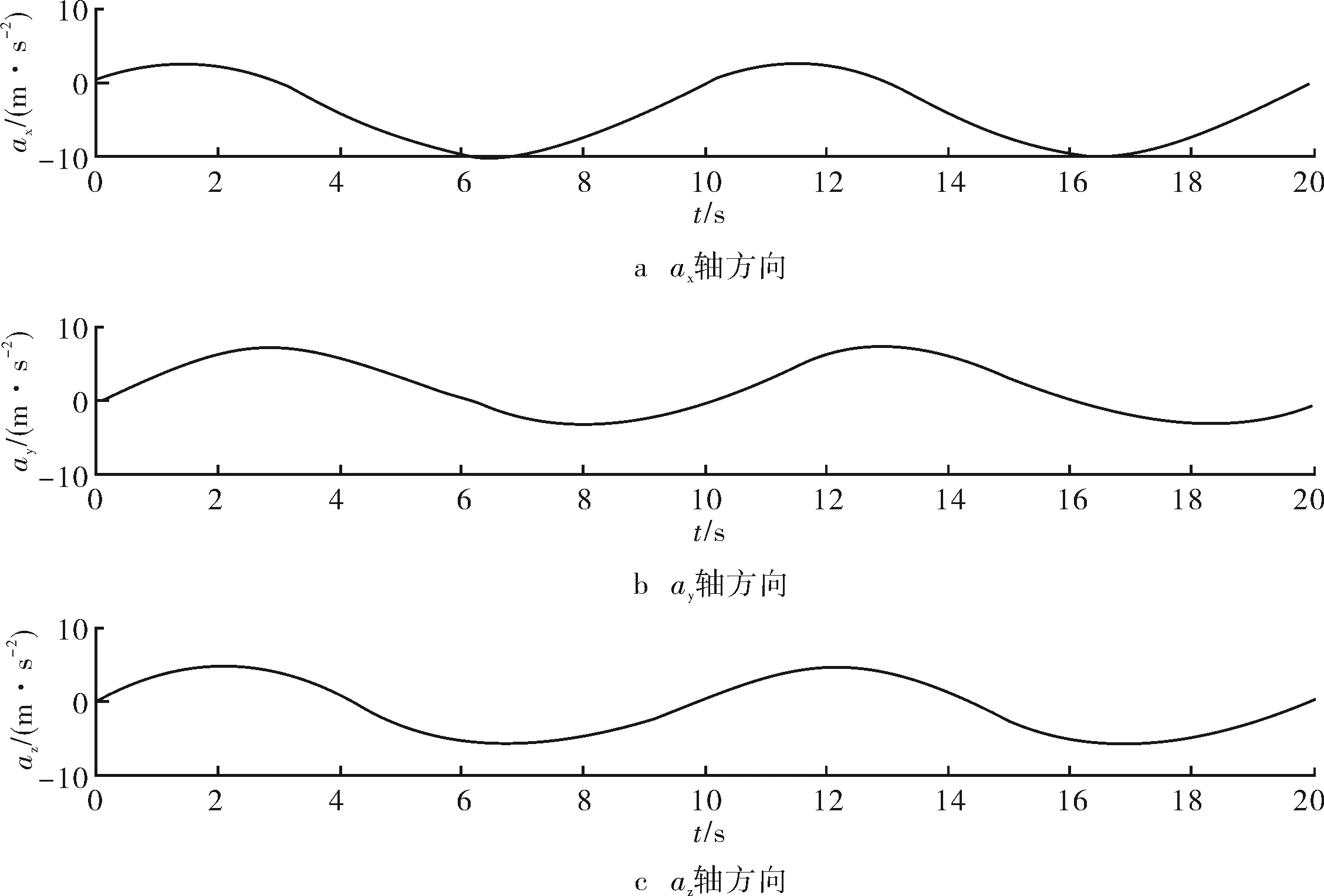
图8 加速度信号

图9为通过FFT变换和频域计算的方法求解出的位移随时间变化曲线。

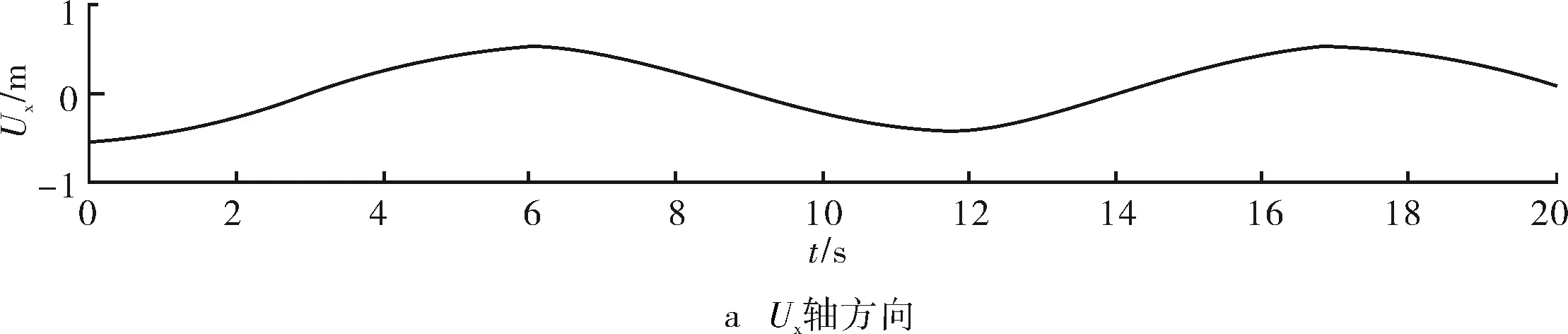
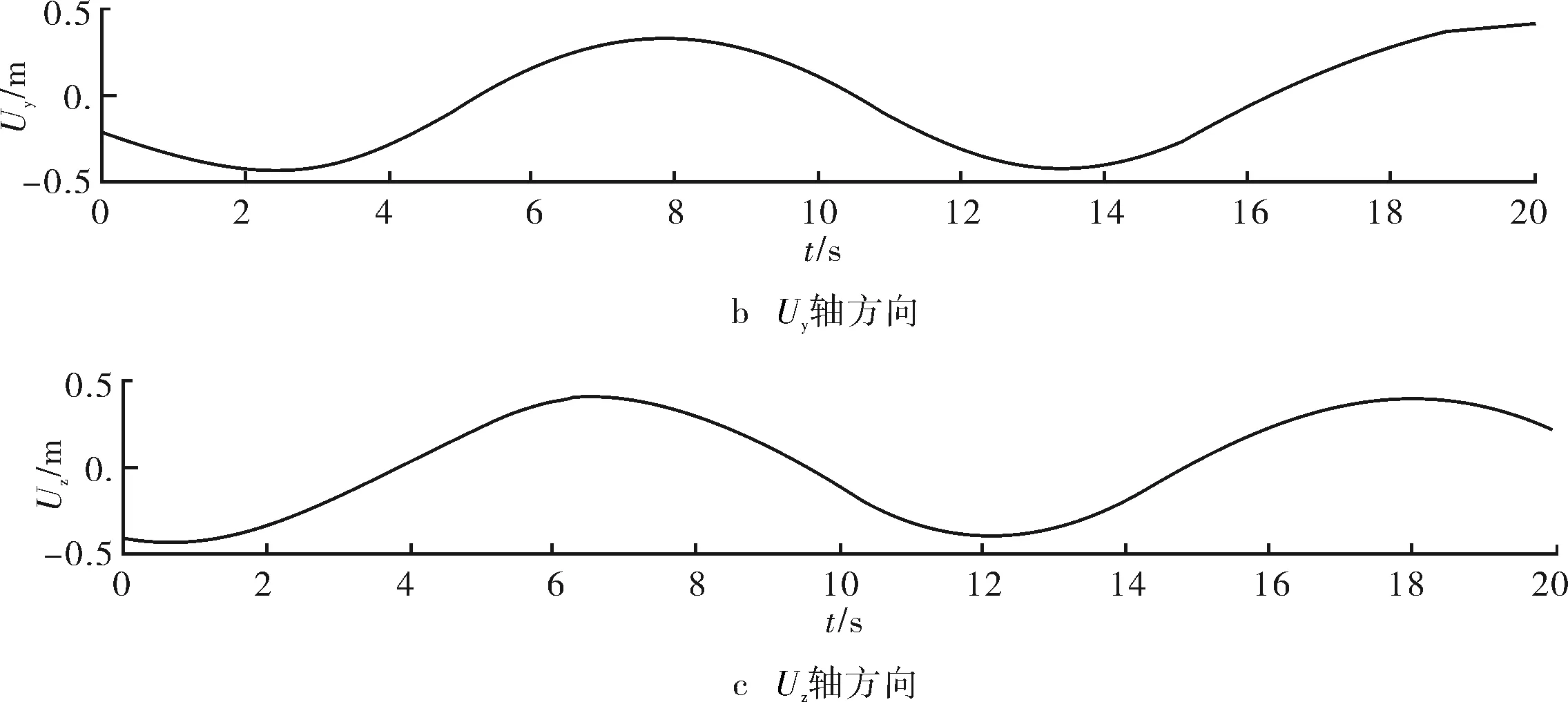
图9 位移信号

由计算结果可知，重力加速度总量在单一象限内随时间而周期变化。其中，重力加速度在x轴方向上的分量变化最大，在z轴方向上的分量变化最小。同时，对应的位移信号均随时间而周期变化，其中位移信号在z轴方向上变化最大，在x轴方向上变化最小，说明柔性管缆在垂直方向受到外载荷的影响最大。因此，在关于柔性管缆的防护工作中，应着重考虑垂直方向上的影响。

5 结语

本文应用四元数法和4阶Runge-Kutta法对柔性管缆进行姿态角更新求解，应用FFT变换和频域计算的方法推导出柔性管缆3个方向位移的计算公式，并运用MATLAB计算其位移值。该方法具有计算量小，运算快，程序简单等优点。通过对位移数据的分析，柔性管缆在垂直方向受到外载荷的影响最大，为柔性管缆弯曲强度和疲劳强度计算提供一定理论依据，也为柔性管缆的设计与防护提供数据支持。