钻齿侵入破碎非均质花岗岩机理研究

刘和兴，罗云旭，刘伟吉，柳亚亚，吴艳辉，蔡 饶，祝效华

(1. 中海石油(中国)有限公司 湛江分公司，广东 湛江 524057; 2. 西南石油大学 机电工程学院，成都 610500)

岩石的破碎效率影响着钻井作业的效率。岩石破碎的实质就是钻齿和岩石的相互作用，其基本方式一般可分为切削破岩和侵入破岩2种[1]，两者的主要区别是切削破岩时钻齿的运动方向和被切削岩石表面平行，而侵入破岩时钻齿的运动方向垂直于岩石表面[2-3]。牙轮钻头钻井[4]、旋冲钻井[5]、冲击钻井[6]等技术是以钻齿侵入破岩模式为主，提高侵入齿的破岩效率对提高这些技术的钻进效率有积极意义。

已有了较多关于钻齿(或压头)侵入机理的研究。

1) 试验方面。

在20世纪50～80年代，GARNIER等[7]、MAURER[8]、BLACK和GREEN[9]就对牙轮钻齿破岩机理开展了大量室内试验工作。此后，东北工学院采矿系岩石破碎研究组[10]进行了单齿侵入破岩试验研究，将侵入载荷和侵入深度曲线划分为过渡阶段、弹性变形阶段、塑性变形阶段，同时将岩石破坏区域由内到外划分为粉碎区、破碎区以及裂缝区。余静[11]进行了压头侵入岩石试验，刘明宇等[12]利用光弹试验研究了单齿压入作用在岩石内部产生的应力场。最近，林敏等[13]开展了斧形齿、楔形齿及锥形齿单齿压入砂岩和灰岩的试验，试验结果表明，斧形齿的破碎比功与楔形齿相当，稍高于勺形齿。

2) 理论方面。

压头侵入岩石的最简单模型为单点集中载荷作用下应力响应(称为“Boussinesq”问题)。LAWN等[14-16]得出了点载荷作用下的Boussinesq应力场，并基于格里菲斯裂纹理论，研究了压头下方岩石的裂纹萌生和扩展情况。LINDQVIST[17]得出了双点载荷作用下的Boussinesq应力场云图，解析计算结果解释了中间裂纹和径向裂纹产生机制；KOU等提出了一种预测各种压头引起岩石中压痕深度和径向/中间裂纹分布的方法[18]；此外，为了明确岩石的侵入过程，人们提出了一些简化的“压头-岩石”相互作用模型，如空腔膨胀模型[19-21]。

3) 数值仿真方面。

HUANG等[22]、CARPINTERI等[23-24]利用有限元法(FEM)模拟了压头侵入下岩石的失效断裂情况。TAN等[25]利用位移不连续法(DDM)分析了侧向裂纹的特征，HUANG和DETOURNAY[26]、ZHANG等[27]采用离散元(DEM)，模拟岩石的非均质性，探讨了压头侵入下岩石裂纹的萌生和扩展。ALEHOSSEIN等[28]利用FRANC软件计算了球形齿作用下裂纹尖端的正应力和剪切应力强度因子。LIU等[29]基于REPA程序开发了R-T2D程序，研究了单齿和多齿侵入时岩屑坑的形成过程。石祥超等[30]应用FLAC3D模拟了单齿加载速度对单齿侵入破岩的影响。

上述研究侧重于对破岩机理的研究，对侵入齿的齿形因素考虑较少。为了探究不同齿形侵入非均质硬岩的破岩效率差异，为牙轮钻头和冲击钻头等钻具的选齿提供参考，笔者首先基于Voronoi细分方法建立了2种花岗岩(灰白色和浅红色花岗岩)的有限元模型，并对该模型的参数进行了标定，然后对2种花岗岩建立了5种不同钻齿侵入破碎花岗岩模型，对比分析了这些齿在特定侵入载荷下的岩石破碎情况。

1 基于Voronoi细分的花岗岩有限元模型

岩石是破岩工程的主要作用对象，建立相对准确的岩石模型对于正确认识破岩过程和钻齿的优化工作至关重要。本节以2种花岗岩为对象，基于Voronoi细分的方法建立这2种岩石的有限元模型，并对其模型参数进行标定，为比较不同齿形侵入花岗岩的破岩效率差异打下基础。

1.1 建模过程

Voronoi细分在自然科学、工程、几何学等领域有着广泛的应用。通过Voronoi划分得到的图称为Voronoi图。俄罗斯数学家 VORONOI于1908年提出了N维 Voronoi图的定义[31]。Voronoi划分的主要思路是通过临近原则将N维空间体进行剖分，使其成为无数多面体的集合体(如二维情况即将空间平面剖分成无数多边形的集合体)。每个多面体事实上是依靠其内部的1个核心点控制生成的，每个核心点的影响域是由至该点的距离最近的点组成的集合(临近原则)，该核心点的影响域即构成相应的多面体。生成 Voronoi图的初始点称作Voronoi图的发生元(或种子)[32]。在岩土工程中，Voronoi细分常用于生成块体几何体[33]。为了表述花岗岩的非均质性，基于Voronoi细分和有限元建立了非均质花岗岩模型。具体的过程为：

1) 由矿物组分与矿物粒径生成矿物种子。

根据花岗岩的X衍射试验和CT扫描试验大致确定出花岗岩内部的矿物组分以及矿物的粒径范围。在特定空间(一般为花岗岩计算区域的大小)生成随机分布的球体(简称矿物种子)，每1个球体代表1种矿物颗粒，赋予其矿物属性。依据矿物种子的直径大小控制矿物颗粒的粒径，通过计算每种矿物种子空间体积之和占该特定空间的比值确定每种矿物的组分，即：

(1)

(2)

式中：ωA为A类矿物的质量分数，%；ρA为A类矿物的密度，kg/m3；ViA为A类矿物的第i个矿物种子的体积，m3；ρt为花岗岩密度，kg/m3；Vt为花岗岩体积，m3；n为孔隙率;riA为A类矿物的第i个矿物种子的球半径。

2) 建立矿物仓。

三维Voronoi细分是将三维空间，即D∈R3的1个区域划分成1组多面体。在D内存在由多个矿物种子的球心坐标组成的种子点{Si,xi}，每个种子点根据如下方法被分配1个Voronoi多面体(称为矿物仓)，即：

Ci={P(X)∈D|d(P,Si)≤d(P,Sj),∀i≠j}

(3)

式中，d(P,Si)和d(P,Sj)为欧几里德距离[34]。

所有的Voronoi多面体组成三维Voronoi细分，每个矿物仓具有特定的矿物属性。

3) 模型单元分仓赋材。

创建花岗岩零件，并将该零件划分网格，判断每个网格单元的空间位置与矿物仓的空间位置关系，根据单元与矿物仓之间的位置关系对单元分仓赋予材料属性。单元与矿物仓之间的关系大致分为2类。若单元的所有节点都位于某一矿物仓中，因此该单元被识别并继承这类矿物属性；相反地，若单元的节点分别位于2(或以上)矿物仓内部，则将该单元视为矿物边界(粘结)，赋予其边界材料属性。基于Voronoi细分的花岗岩模型建模示意图如图1所示。

1.2 花岗岩参数标定

本文以2种花岗岩为研究对象，分别为浅红色花岗岩和灰白色花岗岩，其微观结构如图2所示。这2种花岗岩主要由5种矿物成分组成，其中浅红色花岗岩石英占比19.3%，钠长石47.5%，绿泥石2.1%，斜长石21.9%，白云母9.3%；灰白色花岗岩石英占比12.2%，钠长石34.5%，绿泥石4.4%，斜长石41.1%，白云母7.8%。此外，通过微观显微观察发现2种花岗岩的矿物结构都是呈现几何多边形，且具有明显的几何非均质特性。分别建立2种花岗岩的单轴压缩试验和巴西劈裂试验数值模型。通过对岩石单元分区块赋予材料属性建立花岗岩的有限元模型，并多次“试错”、“穷举”，以试验测定的单轴压缩强度、抗张强度和弹性模量为基准，不断调整花岗岩的各种矿物力学参数，最终得到了两种花岗岩的微观力学参数。单轴压缩仿真试验中，花岗岩的模型大小为：ø25 mm×50 mm；巴西劈裂仿真试验中，花岗岩的模型大小为：ø25 mm×25 mm。

图1 基于Voronoi细分的花岗岩模型建模示意

图2给出了灰白色花岗岩材料参数标定模型(浅红色花岗岩模型类似)，仿真试验中将顶部加载板和底部加载板设置为刚体。2种仿真标定试验中的边界及加载参数均为：底部加载板固定；顶部加载板给定向下的恒定速度v=1 mm/s。此外，顶部、底部加载板与花岗岩通用接触，花岗岩内部单元之间自接触，所有接触之间的摩擦因数均为0.25。岩石采用修正的线性D-P(Drucker-Prager)作为屈服准则；同时，仿真中采用塑性应变作为判断岩石破碎失效的依据，相关细节请参考文献[35-36]。

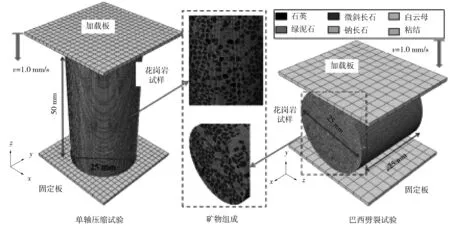
图2 灰白色花岗岩材料参数标定模型

单轴压缩试验中，其应力的计算表达式为：

(4)

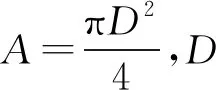
这样通过监测岩石单轴压缩试验中的应力-应变曲线，即可得到待标定岩石的单轴抗压强度和弹性模量。

同理，在巴西劈裂试验中也可得到待标定岩石的抗张强度，试验中的抗张强度为[37]：

(5)

式中：σt为岩石抗张强度，Pa；Fmax为岩石受压过程中对端部加载板的最大反力，N；D为岩石试样的直径，m，此处D=0.025 m；L为岩石试样的直径，m，仿真中取L= 0.025 m。

通过计算实物试验和仿真试验可以得到标定的目标物理量的相对百分误差，即可验证表参数的有效性。其中待标定的3个目标物理量分别为单轴压缩强度、抗张强度和弹性模量。这些目标物理量的相对百分误差的计算方法为：

(6)

式中：εr为目标物理量的相对百分误差，%；Me为目标物理量的试验值；Me为目标物理量的仿真值；目标物理量为单轴压缩强度、抗张强度和弹性模量中的1个。

灰白色花岗岩材料标定试验曲线如图3所示。由单轴压缩试验曲线知道，由于实际的花岗岩内部存在天然的孔隙和裂隙，在试验的初始阶段花岗岩经历了压实阶段，花岗岩存在压实效应，且由压实效应导致的岩石等效塑性应变约为0.05%。单轴压缩实物试验中，灰白色花岗岩的单轴压缩强度和弹性模量分别为101.96 MPa和30.69 GPa；仿真试验得到的单轴压缩强度和弹性模量分别为97.83 MPa和28.80 GPa，相对百分误差分别为4.05%和6.16%。同样，在巴西劈裂实物试验中，其中1组岩样的抗张强度为9.00 MPa，仿真试验得到的结果为9.41 MPa，相对百分误差为4.56%。各个目标物理量的相对百分误差均小于7%，标定有效[38]。最终标定得到的灰白色花岗岩矿物组分力学属性如表1所示。

图3 灰白色花岗岩材料标定试验曲线

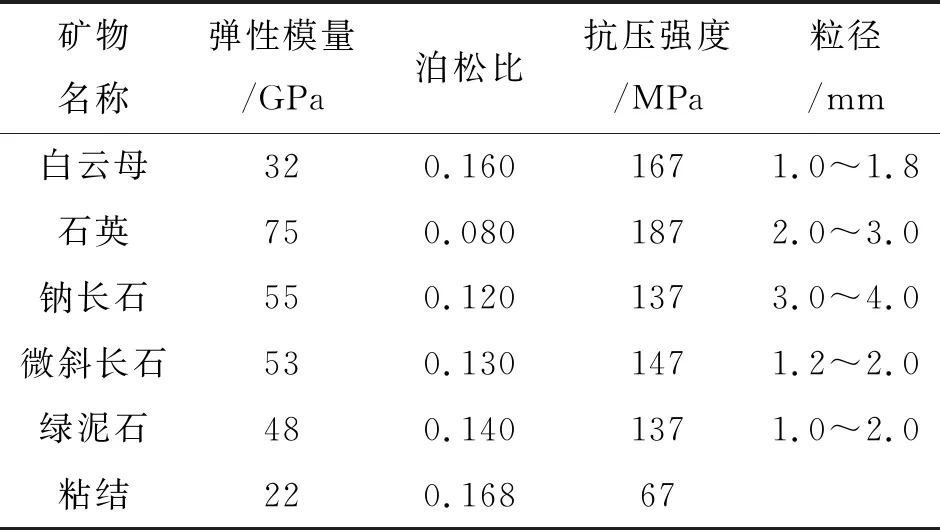
表1 灰白色花岗岩矿物组分力学属性

做出浅红色花岗岩材料标定试验曲线，如图4所示。由图4a中的单轴压缩试验曲线知道，同灰白色花岗岩一样，浅红色花岗岩也存在压实效应，且由压实效应导致的花岗岩等效塑性应变约为0.2%，远大于灰白色花岗岩的0.05%。由此可知，浅红色花岗岩岩石内部孔隙及天然裂隙大于灰白色花岗岩。单轴压缩实物试验中，浅红色花岗岩的单轴压缩强度和弹性模量分别为81.80 MPa和22.49 GPa；仿真试验得到的单轴压缩强度和弹性模量分别为81.02 MPa和23.32 GPa，带入式(6)得到相应物理量的相对百分误差分别为0.95%和3.69%。同样，在巴西劈裂实物试验中，其中1组的岩样的抗张强度为5.76 MPa，仿真试验得到的结果为5.39 MPa，相对百分误差为6.42%。各个目标物理量的相对百分误差均小于7%，标定有效。最终标定得到的浅红色花岗岩矿物组分力学属性如表2所示。

图4 浅红色花岗岩材料标定试验曲线

表2 浅红色花岗岩矿物组分力学属性

从上面的建模过程和岩石标定结果可以看出，基于Voronoi细分方法建立的花岗岩有限元模型能够反应出岩石的一部分非均质特性，这可为利用有限元研究“岩石-刀具”相互作用关系的破岩机理提供一种新思路。另一方面，为了更真实地表征岩石非均质特性，该模型还有进一步完善和改进的方面，如,将真实岩石内部存在的缺陷和孔隙等因素考虑进来。

2 钻齿与岩石相互作用模型

为了优选钻齿的齿形，对2种花岗岩建立不同齿形和压入载荷下的单齿侵入破岩模型，分析这些齿形在特定侵入载荷下的破岩情况，为牙轮钻头和冲击钻头的选齿提供参考。

2.1 钻齿与岩石相互作用模型

单齿侵入破碎花岗岩的数值仿真模型中包括侵入齿和花岗岩2个部件。其中，花岗岩包括浅红色和灰白色花岗岩2种，其模型为25 mm×25 mm×20 mm的长方体；侵入齿参照《矿山、油田钻头用硬质合金齿》(GB/T 2527-2008)[39]选用了其中的CB型、CS型、CS-1型、CX型和CX-1型共5种齿形。各侵入齿的几何信息如表3所示。在建模时，将侵入齿与岩石接触的区域网格细分，细分区域为ø20 mm×20 mm的圆柱区域。在细分区域通过Voronoi细分的方法建立花岗岩的有限元模型，其中各种矿物的组分、各个矿物颗粒及粘结的力学属性见花岗岩材料标定部分；岩石非切削区域(即网格细化区域之外的区域)的材料设置为“石英”的力学属性。

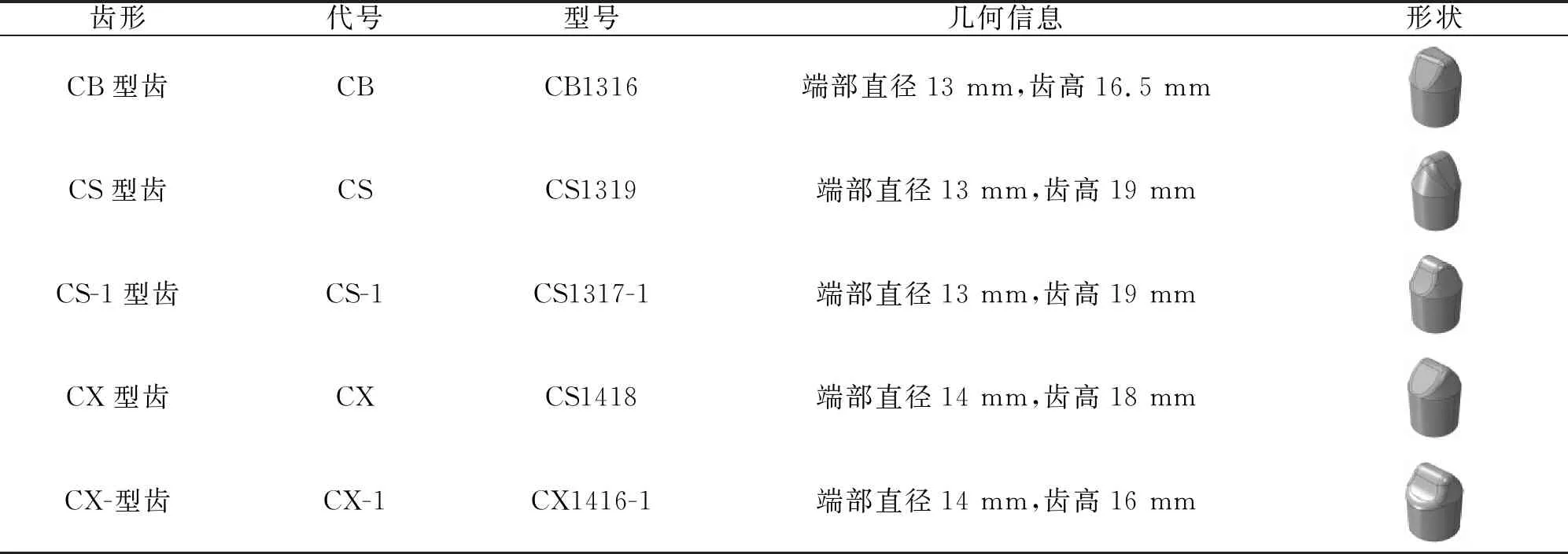
表3 仿真用侵入齿的几何信息

为便于计算与分析，对钻齿与岩石相互作用进行基本假设：钻齿的强度和硬度远高于岩石的强度和硬度，因此将钻齿假设为刚体，且给定其密度为7.08 kg/m3。忽略侵入过程中的侵入齿磨损，当岩石单元失效后即从岩石中删除，忽略其失效后对后续侵入的影响。所有模型中边界及加载参数均为：岩石非侵入区域(即网格细化区域之外的区域)的底部固定，在岩石的底部固定约束；侵入齿与花岗岩接触属性为通用接触，花岗岩网格细化区域内部单元之间自接触，所有接触之间的摩擦因数均为0.25，控制侵入时间为0.005 s。通过改变侵入齿的形状、调整侵入载荷、更换岩石模型来研究不同侵入齿的破岩规律。模型中每种侵入齿的侵入力F=1～4 kN，增量为1 kN。CB型齿侵入破碎灰白色花岗岩数值仿真模型如图5所示。

2.2 结果讨论与分析

图6是当侵入力为4 kN时侵入齿的侵入位移随侵入时间的变化规律。从图6可以看出，在侵入的最开始阶段，侵入位移迅速增大至1个峰值。随着时间的推移，侵入位移在首次侵入的峰值的附近反复波动。出现这种波动情况的原因可能是在侵入初期岩石内部储存的弹性能量的释放。侵入齿在侵入初期除了对岩石产生1部分的破碎外，剩下的能量以弹性能量的形式储存在岩石内部。由于侵入载荷是恒定的，所以当侵入齿侵入至一定深度时，为了维持恒定的侵入载荷(侵入力)，侵入齿反而会出现反向位移。图6中各曲线呈现出的波动情况就是维持侵入齿恒定载荷动态恒定和岩石内部弹性能量存储-释放交替过程的体现。

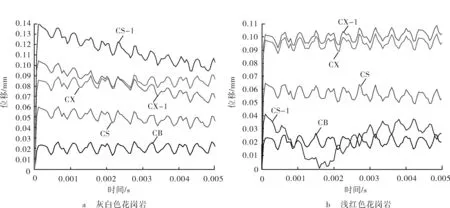
图6 当侵入力为4 kN时侵入位移随侵入时间的变化规律

为了探究各侵入齿在破岩过程中的破岩比功，需要计算各侵入齿在恒定载荷下的位移，以此来计算破岩过程中的能耗。由图6的分析知道，各侵入齿在破岩过程中的位移并不恒定。因此，这里选取各侵入齿在破岩过程中的最大位移作为研究对象。图7 为单齿侵入破碎花岗岩数值仿真中侵入齿的位移随侵入力的变化规律。从图7可以看出，各侵入齿作用下，随着侵入力的增大，侵入位移也相应增大。由于仿真中给定的载荷是静载荷，所以各侵入齿的最大位移的量级在0.15 mm以内。

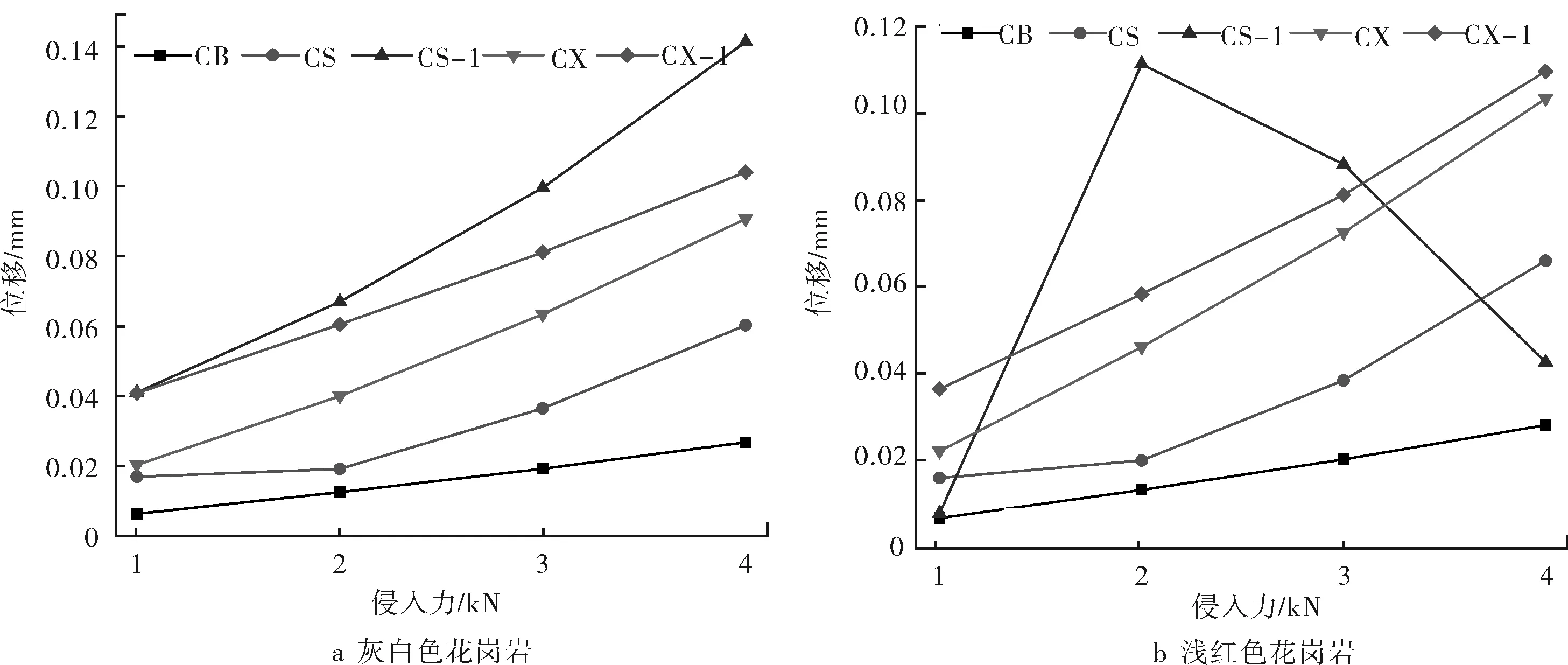
图7 单齿侵入破碎花岗岩中侵入位移随侵入力的变化规律

图8给出了当侵入力为4 kN时各侵入齿破碎2种花岗岩的破碎痕迹。从图8可知，CB型齿对2种岩石造成的损伤范围最小。另一方面，在侵入浅红色花岗岩的过程中，侵入力为1 kN和2 kN时，CB型齿不能对岩石造成损伤，其他齿均能对其造成损伤。且当侵入力为1 kN，侵入灰白色花岗岩时，CB型齿也不能对岩石造成损伤，而其他齿均能对岩石造成损伤。上述情形均表明CB型齿的侵入性能最差。

图8 当侵入力为4 kN时各侵入齿破碎2种花岗岩的破碎痕迹

为了比较其他侵入齿的侵入性能的优劣，需要计算各侵入齿破岩过程中的破碎比功。由上述分析知道了侵入位移和侵入载荷。单齿侵入破碎花岗岩仿真中各侵入齿的破碎比功计算公式[40]为：

(7)

式中：MSE为破碎比功，MPa；Ve为等效破碎体积，mm3；W为外力做功，J；Di为第i个单元的刚度损伤，无量纲；Vi为第i个单元的体积，mm3；k为刚度损伤值大于0的单元总个数；F为侵入力，kN；Xd为侵入齿位移，mm。

图9给出了单齿侵入破碎花岗中破碎比功随侵入力的变化规律。由图9知道，随着侵入力的增加，各侵入齿的破碎比功急剧下降，最后在载荷为3～4 kN时，破碎比功就下降得有限(30～100 MPa)。这表明增大侵入力更能对岩石造成损伤，但载荷为3～4 kN就能取得相对较低的破碎比功(较高的破岩效率)。

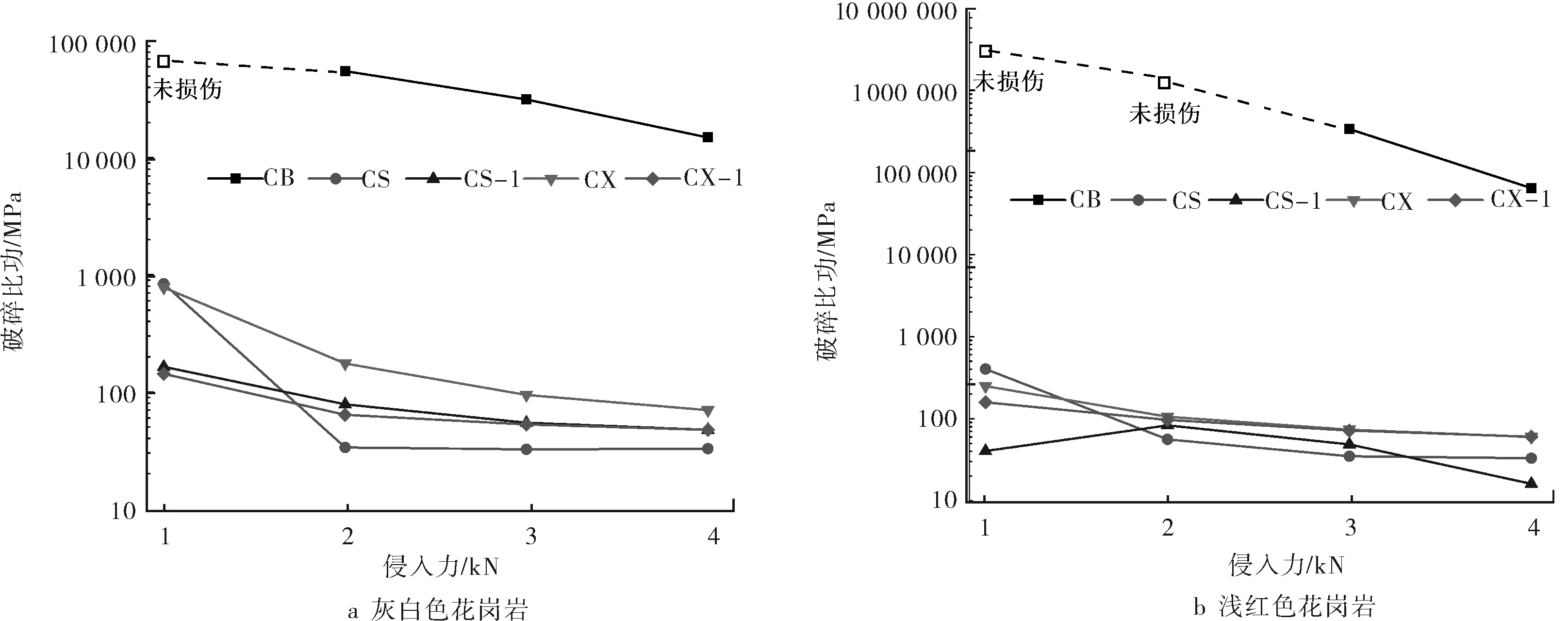
图9 单齿侵入破碎花岗中破碎比功随侵入力的变化规律

在侵入破碎2种花岗岩时，破碎比功最大(即破岩效率最低)的是CB型齿，这与前面分析的结论相吻合。在侵入破碎灰白色花岗岩，且侵入力大于2 kN时，破碎比功最小的3种侵入齿分别为CS型齿、CX-1型齿和CS-1型齿。同样地，在侵入破碎浅红色花岗岩，且侵入力大于2 kN时，破碎比功最小的3种侵入齿大致为CS型齿、CS-1型齿和CX-1型齿。由此可以看出，在这5种侵入齿中，CS型齿的侵入性能最优。

3 结论

1) 本文着眼于“岩石-钻齿”相互作用模式中的侵入破岩方式，聚焦于不同齿形侵入破碎花岗岩的效率差异。基于Voronoi细分方法建立了2种花岗岩(灰白色和浅红色花岗岩)的有限元模型，并对该模型参数进行了标定；建立了5种不同钻齿侵入破碎花岗岩的仿真模型，并分析和对比了这些齿在特定侵入载荷下的破岩情况。

2) 基于Voronoi细分方法建立的花岗岩有限元模型能够反应出岩石的一部分非均质特性，这可为利用有限元研究“岩石-刀具”相互作用关系的破岩机理提供一种新思路；为了更真实地表征岩石非均质特性，可通过将真实岩石内部存在的缺陷和孔隙等因素加以考虑来完善和改进基于Voronoi细分方法建立的花岗岩模型。

3) 恒定侵入载荷下，初始时，侵入位移迅速增大至1个峰值，最大位移在0.15 mm内。随后由于侵入初期岩石内部储存的弹性能释放和侵入载荷的作用下，侵入位移在首次侵入的峰值的附近反复波动。

4) 2种花岗岩中，随着侵入力的增大，侵入位移也相应增大；增大侵入力更能对岩石造成损伤，但载荷为3～4 kN就能取得相对较高的破岩效率；5种侵入齿中，CB型齿的侵入性能最差，CS型齿的侵入性能最优。