一道竞赛不等式的再推广
2022-02-11 06:29陕西省西安市高陵一中710200
中学数学研究(江西) 2022年2期
陕西省西安市高陵一中 (710200) 胡 艳
题目(2020泰国数学奥林匹克不等式)已知a,b,c∈R+,a+b+c=3,求证:
文[1]对(1)的证明方法,变式及推广做了探究,将(1)推广为:

本文拟从不等式(1)的结构的变化出发,对推广作进一步的分析,为了表述的方便,由柯西不等式可得:

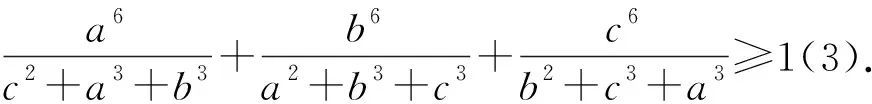


不等式(3)结构对称,进一步,对其分母得到项添加系数并推广至n个元素有:

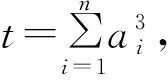
显然,当v=0时,推广2即为推广.若对推广2中的参数赋值,可得许多不等式.例如令λ=1,μ=2,ν=0,n=3,S=3即为不等式(1).
若对推广2 的指数推广,则又有:

更一般的有如下结论:
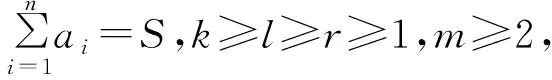

(j=1,2,3).
显然,推广3是推广4的特例,下面只给出推广4的证明.



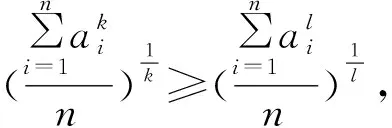


若对上述推广的不等式中的参数赋值,可得许多不等式.例如,在推广4中,若令r=1,l=3,k=5λ=1,μ=2,ν=3,m=2,n=3,S=3就有:

又如在推广3中λ=2,μ=3,ν=4,n=3,k=4,m=2,S=3就有:

再如,在推广3中若令k=4,n=3,m=5,S=3就有:
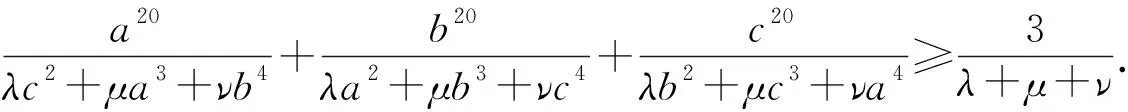
猜你喜欢
意林·少年版(2020年21期)2020-12-10
语数外学习·高中版中旬(2020年2期)2020-09-10
高中生学习·高三版(2017年6期)2017-06-12
中学生数理化·高一版(2017年1期)2017-04-25
小学阅读指南·低年级版(2016年4期)2016-05-14
中学生数理化·高二版(2016年5期)2016-05-14
中学生理科应试(2016年7期)2016-05-14
理科考试研究·高中(2016年9期)2016-05-14
理科考试研究·高中(2014年11期)2014-11-26
数学教学(2013年9期)2013-12-12

