基于数学核心素养发展的指数函数教学设计*
内江师范学院数学与信息科学学院 (641100) 程 双 刘成龙
四川省内江市第六中学 (641100) 张先毅
指数函数是高中数学重要且常见的基本初等函数,是进一步学习数学的基础.具体来说,指数函数是高中函数概念、性质的具体呈现,为学习对数函数和幂函数提供了经验和方法,为后续学习高等数学打下基础.与此同时,指数函数还是发展学生数学核心素养的良好载体.因此,本文立足于数学核心素养对指数函数进行教学设计,旨在学生对指数函数理解的基础上发展学生数学核心素养.
一、数学核心素养与数学教学
什么是数学核心素养?马云鹏认为:“数学核心素养是学生学习数学应当达成的有特定意义的综合性能力”[1];赵思林认为:“数学核心素养是个体在四基基础上所形成的数学眼光,数学思维方式,数学经验,数学信念,数学价值观等”[2];《普通高中数学课程标准(2017年版)》(下文简称《课标2017》)指出:“数学学科核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现,是在数学学习和应用的过程中逐步形成和发展的”[3],等等.可见,核心素养的概念界定普遍较为抽象,这为一线教师认识核心素养带来了难度.于是,《课标2017》提出了数学学科核心素养包含的具体素养:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.[3]这六大素养的提出为一线教师明确了数学教学中应发展的数学学科核心素养.
如何在数学教学中发展核心素养?数学教学是教师引导学生主动地认识客观世界中的数量关系和空间形式,以促进学生身心持续和谐发展的数学活动[4],而数学本身具有高度的抽象性和逻辑的严谨性,正是这些学科特点使得数学活动中充满着数学核心素养:数学概念的形成、命题的提出、模型的建构无处不存在数学抽象;数学运算是数学活动的基本形式[3],是获取数学结果的基本手段,正如章建跃博士所言:数学运算是数学的“童子功”;数学结论的获得需要依靠逻辑推理来实现,如几何学家伍鸿熙所说:逻辑推理是数学的“命根子”;等等.显然,数学教学活动是数学核心素养发展的现实土壤.同时,作为最具学科特色的数学核心素养理应成为数学教学活动顶层设计的理论指导.因此,数学教学中要发展学生的数学核心素养理应做到:依托数学核心素养设计数学教学活动;通过问题解决让学生亲历数学化过程,促进深度学习发生;通过反思活动积累数学经验.
二、数学核心素养视角下的指数函数教学设计
(一)教材分析
本节课选自人教A版高中数学必修一第二章第1节指数函数第二课,内容包括指数函数的概念、图象及性质.指数函数是继高中函数概念后首次学习的基本初等函数,是高中函数概念、性质的直接呈现和应用.
(二)学情分析
在学习指数函数之前,学生已经学习了函数的概念、单调性、奇偶性、最值等基本性质,初步具备研究指数函数的知识、方法和能力.但指数函数一直以来都是学生公认的难点,学生存在一定的畏难情绪.
(三)教学过程
1.创设情境,触发思考
情境1 某种细胞分裂时,每次每个细胞分裂为2个,则1个这样的细胞第一次分裂分成2个细胞,第二次分裂成4个细胞,第三次分裂成8个细胞……
情境2 我国古代学者庄子在《庄子·天下篇》中有一句话:“一尺之棰,日取其半,万世不竭”.
问题1 能用数学式子分别表达情境1、2中所包含的量与量间的关系吗?

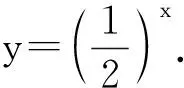
师生活动:在老师的引导下,学生观察表达式得出共同特征,并给出统一表达式:y=ax.
设计意图:创设问题情境,引导学生从现实情境中抽象出数学问题,这一过程属于水平数学化.对问题1得出的两个函数表达式再抽象出具有一般性的式子,这一过程属于垂直数学化.基于水平数学化和垂直数学化思想提出具有指向性的问题,引导学生把握问题本质,挖掘题中的隐含条件,进行抽象,列出表达式并建立相应模型,发展数学抽象和数学建模素养.
2.合作探究,建构新知
问题3 y=ax是函数吗?
教师活动:引导学生分类思考.
预设:学生通过讨论达成共识:当a=0,x取非正数时,y=ax无意义,不构成函数;当a<0,x取分数且分母为偶数时,式子无意义,不构成函数;当a>0时,y=ax构成函数,并且a=1时为常数函数.
在此基础上,教师点明本节课的主题——指数函数.
问题4 能根据前三个问题的探究归纳得到指数函数的概念吗?
学生活动:学生得出函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量.
追问1 自变量x的取值范围是什么呢?
学生活动:讨论得出当x取一切实数时,函数表达式都有意义,即函数的定义域为R.
设计意图:通过问题3,引导学生分类讨论,对y=ax是否为函数进行判断.既训练了学生逻辑推理能力,也感知了数学的严谨性.对问题3进行抽象,得到问题4,让学生从一般的数学问题抽象出更高层次的数学问题,发展数学抽象素养.
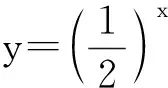
学生活动:学生通过列表、描点、连线作出函数图象,如图1.
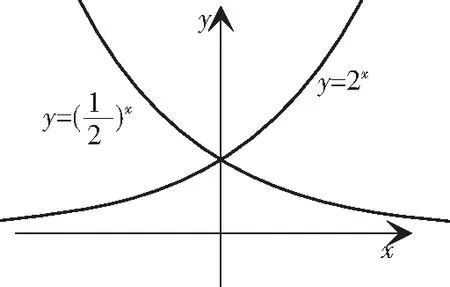
图1

学生活动:学生作出函数图象,如图2.

图2
探究根据函数图象的走势能得到什么结论?
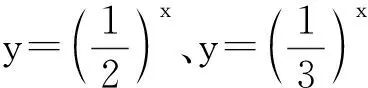
设计意图:学生借助函数图象,将抽象的符号变成直观的图形,建立数与形的联系.通过图形,观察变化规律、归纳得出结论,发展直观想象素养.
追问3 根据图象,你能得出那些指数函数的性质?
学生活动:学生归纳出性质:
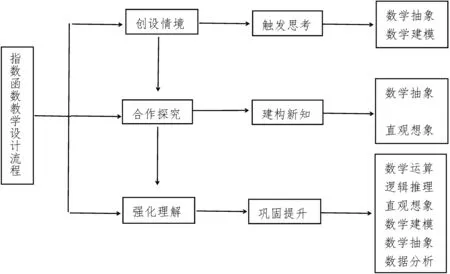
(1)当底数a>1时,指数函数在R上单调递增,当底数0 (2)指数函数都过定点(0,1); (3)指数函数的值域为(0,+∞). 教师活动:教师借助几何画板验证学生得出的性质. 师生活动:师生共同总结指数函数图象与性质. 设计意图:观察图象归纳出指数函数性质,教师运用几何画板验证,进一步发展数学抽象和几何直观素养. 3.强化理解,巩固提升 例1 指数函数f(x)=ax(a>0,且a≠1)的图象经过点(3,π),求f(0),f(1),f(-3)的值. 设计意图:依据指数运算原理解决问题,不仅强化学生对指数函数的理解,而且在知识的运用过程中培养学生数学运算素养. 例2 设a,b,c,d均大于0,且不等于1,y=ax,y=bx,y=cx,y=dx在同一平面直角坐标系中的图象如图3,试判断a,b,c,d的大小关系. 图3 设计意图:图3是图2的一般化,通过对图2中函数图象所对应数据的分析可以归纳出a,b,c,d的大小关系,并可以抽象出更一般的命题,再根据直线x=1与各函数图象交点的纵坐标大小对命题加以证明.本例意在发展几何直观、数据分析和逻辑推理素养. 例3 比较下列各题中值的大小.(1)1.72.5,1.73; (2)0.8-0.1,0.8-0.2; (3)1.70.3,0.93.1. 设计意图:设置(1)和(2)意在强化学生对指数函数模型的认识,发展数学建模素养.(3)是对(1)(2)的升华,意在进一步发展数学建模素养和逻辑推理素养. 例4 一种产品的产量原来是a,在今后m年内,计划使产量平均每年比上一年增加p%,写出产量y随年数x变化的函数解析式. 设计意图:学生从生活实例中抽象出数学问题,并用数学符号予以表征,意在发展数学抽象和数学建模素养. 本文以数学核心素养为理论指导给出了指数函数教学设计如图4,有效地将数学核心素养与数学教学结合,使得数学核心素养有生根的土壤,并且让数学教学更加科学,让学生的发展更加充分.具体来讲,对问题情景的不断抽象,发展学生的数学抽象和建模素养;在师生合作、生生合作中,抽象得到指数函数的概念,通过绘制图象、直观想象、数学抽象得到指数函数的性质;通过4个例题的解决有针对性地发展学生数学核心素养,充分做到有的放矢.总的来看,本文所提供的指数函数教学设计具有科学性、实用性和合理性. 图4
三、教学反思