矩形混凝土空心墩延性抗震性能试验研究

邵长江 ，漆启明 ，韦 旺 ，肖正豪 ，何俊明 ，饶 钢

（1.西南交通大学土木工程学院，四川 成都 610031；2.泸州市交通建设工程管理中心，四川 泸州 646000）

基于经济和优化受力考虑，空心截面桥墩是大量高墩大跨桥梁的优选设计方案，且多位于地震高烈度区[1].由于空心墩震害方面的经验、试验和理论研究的相对不足，当前公路和铁路桥梁抗震规范[2-3]中空心墩延性设计通常直接套用实心墩的研究成果，由此造成了空心墩延性设计的不准确性[4]，因此延性性能成为空心墩抗震研究的重要课题之一.

截至目前，国内外学者针对空心墩柱的延性抗震性能进行了大量研究[5-14].早期，Mander等[5]研究了轴压比和配箍率对矩形空心墩延性性能的影响，表明箍筋约束效应对空心墩延性、耗能及抗弯承载力均是有利的.我国台湾学者Yeh等[6]的足尺方形空心墩试验发现：箍筋用量满足ACI规范[7]要求（为规定限值的50%时，试件发生弯曲破坏，而配箍率为限值的20%时则发生剪切破坏），Mander约束混凝土本构的数值模拟达到了可接受的精度.Mo等[8]以高强混凝土矩形空心墩剪跨比、箍筋数量及轴压比等为设计参数，试验得出了与Yeh等相同结论.国内学者关于空心墩的试验研究起步较晚，但进展较快.宋晓东[9]的拟静力试验表明，增大壁厚和箍筋率可有效提高空心墩的变形和耗能能力.杜修力等[10-12]通过大比例尺空心墩的拟静力试验发现：大轴压比时配筋率对混凝土空心桥墩性能的影响明显；配筋率相同时增大轴压比，钢筋混凝土空心桥墩的承载力和刚度提高，但延性性能降低；箍筋间距对空心桥墩的承载力影响不大，却能大大改善延性和变形性能.宗周红等[13-14]还进行了双向拟静力试验以模拟空心墩复杂受力行为，为矩形空心桥墩的抗震设计提供了相关建议.尽管现有空心墩研究成果丰硕，但距纳入规范还存在一定差距.因此，有必要结合试验深入分析空心墩地震损伤机理、破坏模式及延性性能，进一步充实和完善空心墩抗震性能设计方法.

故此，以剪跨比、配箍率、纵筋率为设计参数对14个空心墩进行拟静力试验，同时以1个相同外尺寸的方形实心墩作为对比.描述空心墩损伤状态，分析各参数对桥墩滞回性能、曲率延性及位移延性的影响规律，并结合文献数据探讨既有塑性铰公式对空心墩的适用性.研究成果可丰富空心墩抗震性能试验研究，为混凝土空心墩延性设计提供参考.

1 试验概况

1.1 试件设计

试件包括1/4缩尺的7个方形空心墩（D1～D3、E1、E2、F1、F2）、7 个矩形空心墩（G1～G3、H1、H2、I1、I2）及一个方形实心墩（A2），尺寸及配筋如图1所示.方形空心墩尺寸为 500 mm × 500 mm，矩形为 500 mm × 800 mm，壁厚均为 120 mm，墩高分别为 1.95、2.95、3.95 m；方形实心墩外轮廓尺寸为500 mm × 500 mm；墩身和承台均用 C40 混凝土浇筑，纵向钢筋为HRB400，横向钢筋及拉筋采用直径 10 mm 的 HRB335，具体参数如表1.表中：L为桥墩试件的墩高；h为截面高度；ρl为纵筋率；ρs为体积配箍率；s为箍筋间距.各试件的轴压比均为0.05，纵筋率为1.63%～2.81%，体积配箍率为1.34%～3.10%，均满足我国《公路桥梁抗震设计细则》[2]（以下简称《细则》）的相关规定.

表1 桥墩模型设计参数Tab.1 Design parameters of pier samples

图1 桥墩尺寸及配筋Fig.1 Size and bar arrangement of bridge piers

1.2 试验加载及仪器布置

试验在四川省交通运输厅公路规划勘察设计院道桥所实验室进行，试验装置及加载制度如图2所示.试验测试的主要内容为墩顶的水平力、水平位移及墩身曲率等.其中墩身曲率是测试的重点，模型施工时预埋测点，依次测试距承台顶面6、19、38、62、100、150 cm 位置的平均曲率.水平推力由MTS 500 kN高性能全动态作动器提供，其额定行程为 ±250 mm.采用力和位移混合加载制度：桥墩屈服前采用力控制，力幅值为iFy（Fy为理论屈服力，为截面屈服弯矩My与墩高L的比值[2]，i为比例系数，通常范围为0.2～1.5）；桥墩实际屈服时的位移为屈服位移Δy，此后采用位移控制，位移幅值依次为jΔy（j=1,2,3,···）；每级加载工况循环两次，当桥墩承载力下降至峰值荷载的80%时结束试验[12].为便于分析，规定推力为正向加载，反之为负向加载，靠近反力墙侧为E侧，远离侧为W侧.

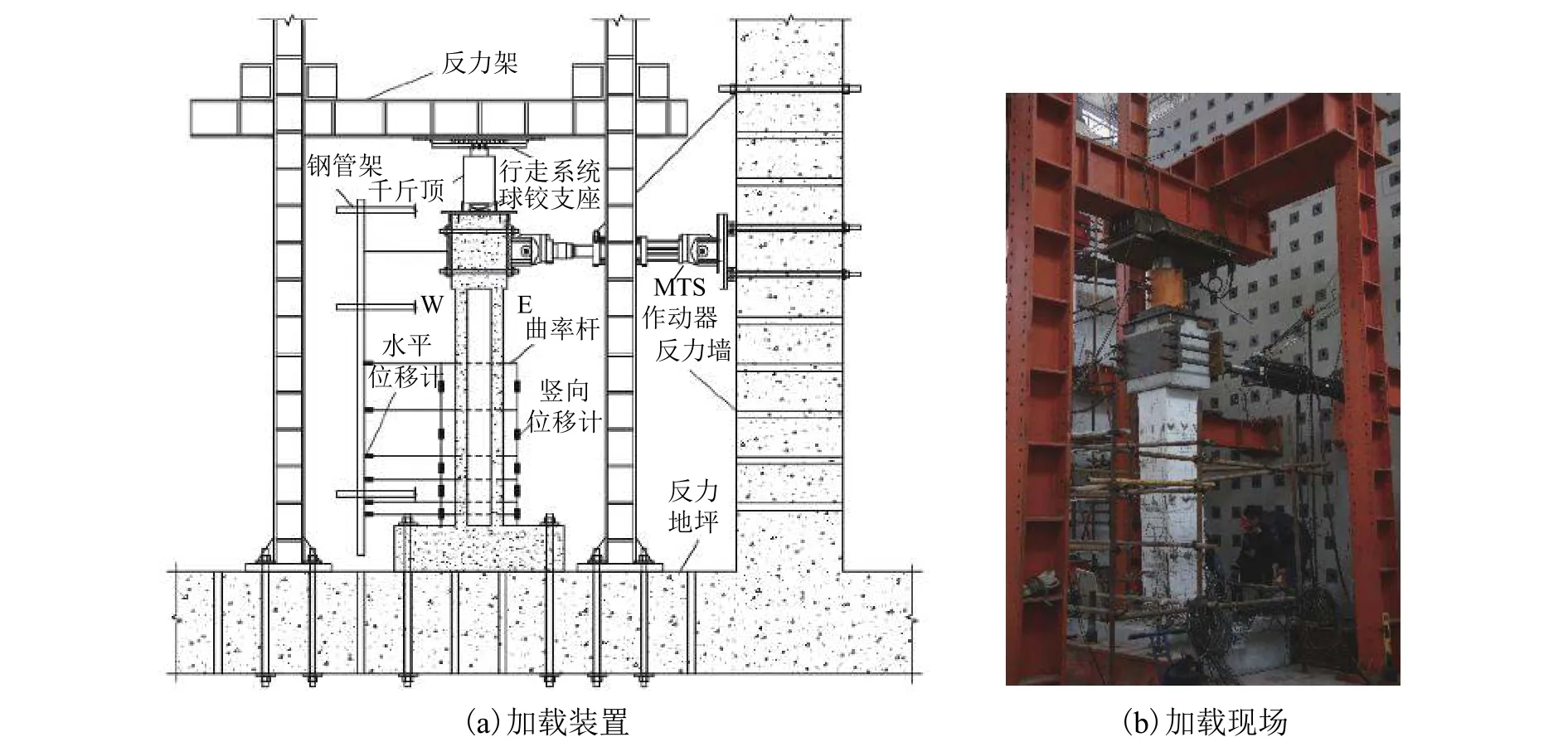
图2 试验装置和加载现场Fig.2 Test setup and loading protocol

2 试验现象与滞回特性

2.1 试件破坏特征

桥墩试件均发生了弯曲型破坏，经历了混凝土微裂缝的出现、正面裂缝局部贯通、侧向裂缝斜向扩展、保护层混凝土局部脱落、保护层大面积剥落，纵筋屈服、纵筋裸露、纵筋屈曲或拉断等过程.以试件D2为例，对试验现象进行描述，图3为墩底W侧的损伤情况.

图3 D2 墩底（W 侧）裂缝发展过程Fig.3 Crack evolution of specimen D2 at pier foot (W side)

墩顶水平力为60 kN时，在E侧距墩底约48 cm处出现一条贯通截面的发丝状裂缝；反向施加60 kN荷载时，试件 W 侧在距墩底 15、33、50、80 cm 位置出现4条新裂缝，其中50 cm处裂缝沿截面贯通，其余3条裂缝虽然较长（约40 cm），但并没有贯通.当墩顶力为100 kN时，已有裂缝宽度不断发展，同时墩身高度范围内又出现了新的裂缝，部分弯曲裂缝向侧面发展形成斜裂缝.在墩顶位移水平24 mm阶段，纵筋已达到屈服应变，此时裂缝数量急剧增加，而在随后工况中新出现的裂缝较少.墩顶位移为72 mm时，墩顶侧向力达到最大值219 kN，此时E侧距墩底高度10、20 cm处裂缝宽度已达到2.01 mm和1.64 mm，此外桥墩与承台连接处的裂缝也较为显著，因此将以上3条裂缝作为重点观测裂缝.在后续加载工况中，上述3条重点裂缝宽度不断扩大，而E侧其余位置裂缝宽度则普遍在0.60 mm以内；同时，在受压侧的脚隅处混凝土表面率先起皮，并伴有明显竖向裂缝生成，混凝土保护层开始剥落.当位移水平为144 mm时，墩顶最大承载力为177 kN，强度下降至峰值的81%，出于安全考虑停止加载并结束试验，最终施加位移为148 mm.其余构件的试验过程和试验现象与D2类似，只是开裂荷载、裂缝发展规律、墩顶位移、最大抗力等不同，不再赘述.

图4给出了不同剪跨比和不同截面桥墩的最终裂缝分布，由此可以分析空心墩的震损机理、破坏模式与实心墩的异同.图中：Δu为桥墩的极限位移.分析剪跨比的影响可知：试件D1（L/h=3.9）的侧面斜裂缝较多，墩底裂缝与竖向的角度大致为60°，桥墩中部裂缝角度约为45°，该区域内的水平和竖向剪应力接近，正面和背面水平裂缝双向扩展形成的斜裂缝交叉形成网格，墩底网格明显较密，破坏时墩底混凝土压溃、纵筋屈曲，为弯曲控制型破坏；试件D2（L/h=5.9）侧面斜向裂缝数量明显减少，且斜裂缝网格较大，墩底裂缝角度约为45°，到桥墩中部时近似为35°；试件D3剪跨比达到了7.9，桥墩侧面仅有少量斜裂缝，所形成的水平裂缝分布均较为规律.上述现象说明剪跨比较小的桥墩更易发生剪切破.试件D1和D2墩底均出现了混凝土压溃和纵筋屈曲现象，而D3的塑性变形主要源于墩身弯曲裂缝，D1和D2墩底曲率较D3更大.

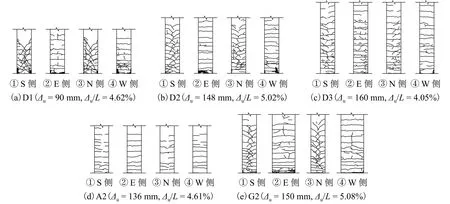
图4 墩身典型裂缝分布Fig.4 Typical crack distribution of specimens

由墩高相同（L/h=5.9）但截面不同的试件A2、D2及G2裂缝分布可见：空心墩弯曲裂缝间距更密集，且分布范围相对较大.尽管桥墩剪跨比为5.9，但空心墩侧面出现了较明显的斜向裂缝，而实心墩几乎均为水平裂缝，表明空心墩抗剪能力较弱.确保弯曲破坏前不发生剪切破坏是空心墩延性抗震设计的前提，但目前公路和铁路桥梁抗震设计规范均未对空心墩的抗剪问题给予特别说明，加之墩底塑性铰区为最不利区域，因此在空心墩抗震设计时应予以重点关注.

2.2 滞回性能

桥墩通常需要在地震中耗散结构所吸收的很大一部分地震能量，且墩身强度降低控制在一定范围内，图5代表性地给出了试件D1和D2的滞回曲线.由图5可知：桥墩开裂前，加载与卸载曲线近似直线，可认为处于弹性状态；桥墩开裂后，试件的截面刚度与整体刚度逐渐下降，滞回环面积开始逐渐扩大，逐渐进入非线性，开始出现残余位移；随着纵筋屈服、塑性铰的形成，滞回环愈发饱满；当水平荷载达到峰值以后，由于纵筋的屈曲、断裂、滑移及混凝土保护层大面积剥落等原因，桥墩承载力开始下降，同时滞回曲线开始出现“捏拢”效应.

图5 试件 D1 和 D2 滞回曲线Fig.5 Hysteretic curves of specimens D1 and D2

3 试验结果分析

3.1 骨架曲线

图6比较了部分试件的骨架曲线.剪跨比对桥墩的水平承载力及位移影响较大，墩顶最大水平位移随剪跨比的增加而增大，而水平承载力随着剪跨比的增大显著减小.低轴压下配箍率变化对空心墩的承载力和延性的影响不大，而增加纵筋率可以在一定程度上提高空心墩承载力和延性能力.在纵向、横向配筋率相近的情况下，方形实心墩相对于方形空心墩有更大的水平承载力，而矩形空心墩的承载力比方形空心墩和实心墩均大.

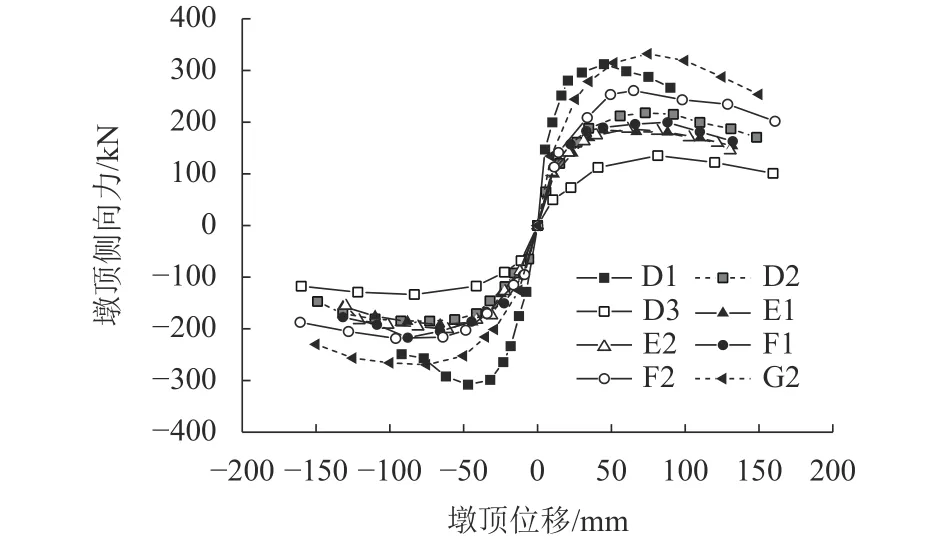
图6 空心墩骨架曲线比较Fig.6 Comparison of skeleton curves of hollow piers

3.2 延性性能

位移和曲率延性系数是衡量空心墩延性性能的重要指标.位移（曲率）延性系数定义为桥墩的极限位移Δu（极限曲率Φu）和桥墩屈服位移Δy（屈服曲率Φy）的比值.利用文献[11]方法计算墩身各节段平均曲率，并假定墩顶处曲率为0，部分结果如图7所示.图中：Δ为不同加载工况的墩顶位移.根据文献[15]方法计算空心墩塑性铰长度Lp实测值，结果如表2所示.

图7 部分空心墩平均曲率分布Fig.7 Average curvature distribution of some hollow piers

分析图7和表2可知：1）各空心墩的μΔ范围在5.1～7.7，表现出较好的延性性能；2）随着墩顶位移增加，墩底潜在塑性铰区域曲率明显变大，而墩身中上部曲率变化则较小，整体处于弹性状态；3）随着剪跨比的增加，空心墩首次屈服位移随之增加，但由于极限状态的差异，延性系数规律性不显著；4）空心墩底部的平均屈服和极限曲率均随着减跨比的增加而有所降低；5）低轴压比下，纵筋率和配箍率对空心墩延性系数的影响规律不够明显，因此在后文将结合文献数据进一步探讨各参数对空心墩延性性能的影响；6）截面高度相同的试件G2延性系数较D2更低，有待后续研究进一步验证.

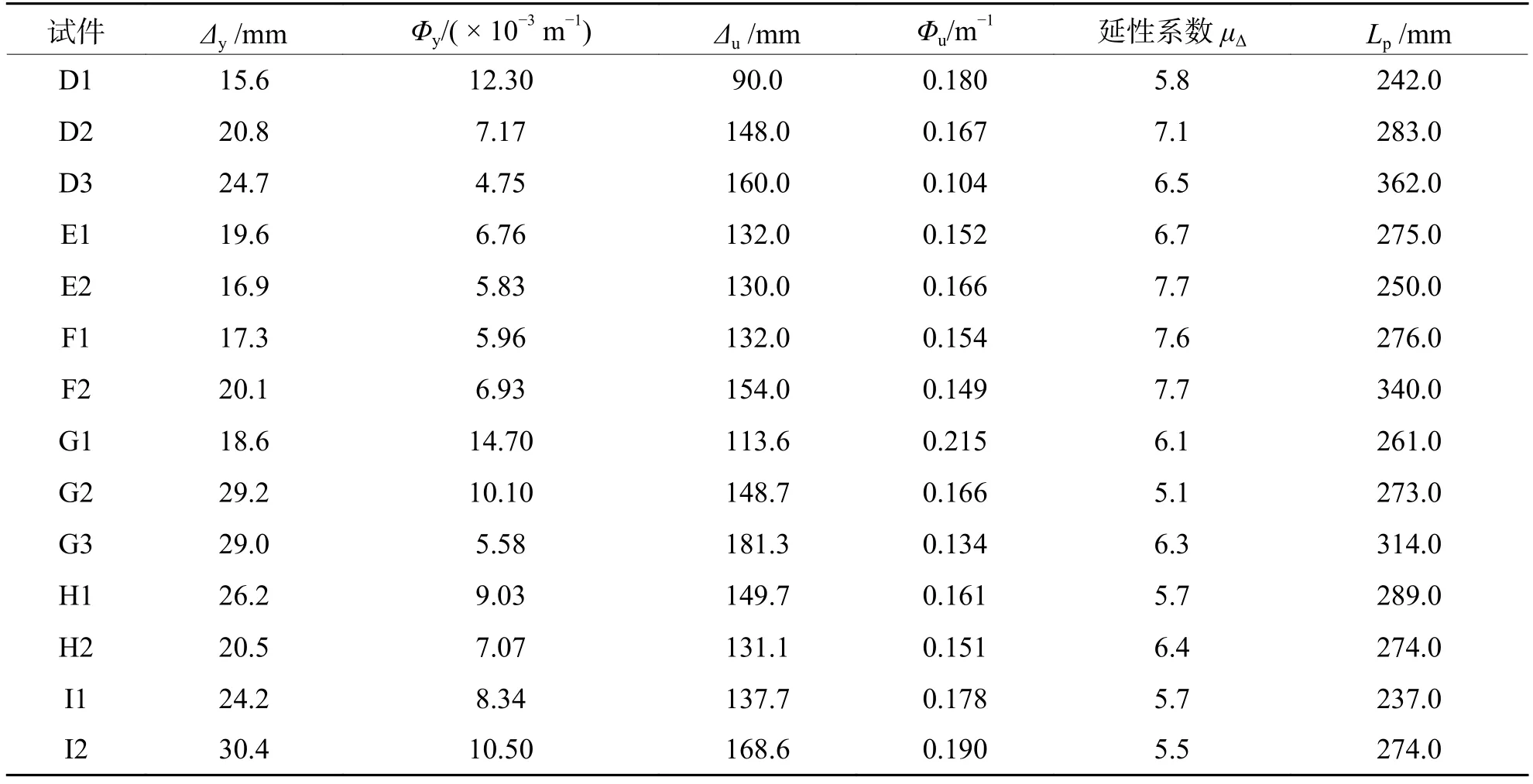
表2 延性系数和塑性铰长度实测值Tab.2 Measured ductility factors and plastic hinge length

4 空心墩位移能力评估

墩顶位移能力估算是桥墩延性抗震设计的重要内容，等效塑性铰模型是目前许多规范采用的计算方法，因此有必要探讨既有塑性铰公式对评估空心墩位移能力的适用性.

4.1 等效塑性铰模型

Lp的概念最早源于钢筋混凝土梁，Park等[15]将塑性铰长度的定义推广至悬臂梁，Priestley等[16]将塑性铰长度应用于桥墩，提出了“等效塑性铰长度”的概念，以考虑墩身剪切变形及钢筋粘结滑移对墩顶位移的影响.学者们在试验基础上提出了众多等效塑性铰长度的计算模型[17-24]，如表3.表中：db为纵筋直径；fy为纵筋屈服强度；Ag为毛截面面积；Pu为轴力；fc‘为混凝土强度；φ为强度折减系数.Paulay- Priestley 模型已被 Eurocode 8[24]、Caltrans[19]以及《细则》[2]等规范借鉴，其中Eurocode 8模型中适当调整了系数，Caltrans限制塑性铰长度最小值为0.044fydb，《细则》在Caltrans的基础上将塑性铰长度进一步限制在2/3截面高度内.

表3 等效塑性铰计算模型Tab.3 Equivalent plastic hinge length models

4.2 影响因素分析

为更全面分析各种参数对空心墩延性系数和塑性铰长度的影响规律，收集整理了部分空心墩试验数据[9,11,14,17,25]，如表4 所示.Mo 等[25]的Lp试验值按文献[15]方法计算，Han等[14]的数据包括 EW和NS两加载方向，其余数据由文献直接给出.表4中顺序编号依次为1～22，表2中空心试件顺序编号依次递增为23～36.

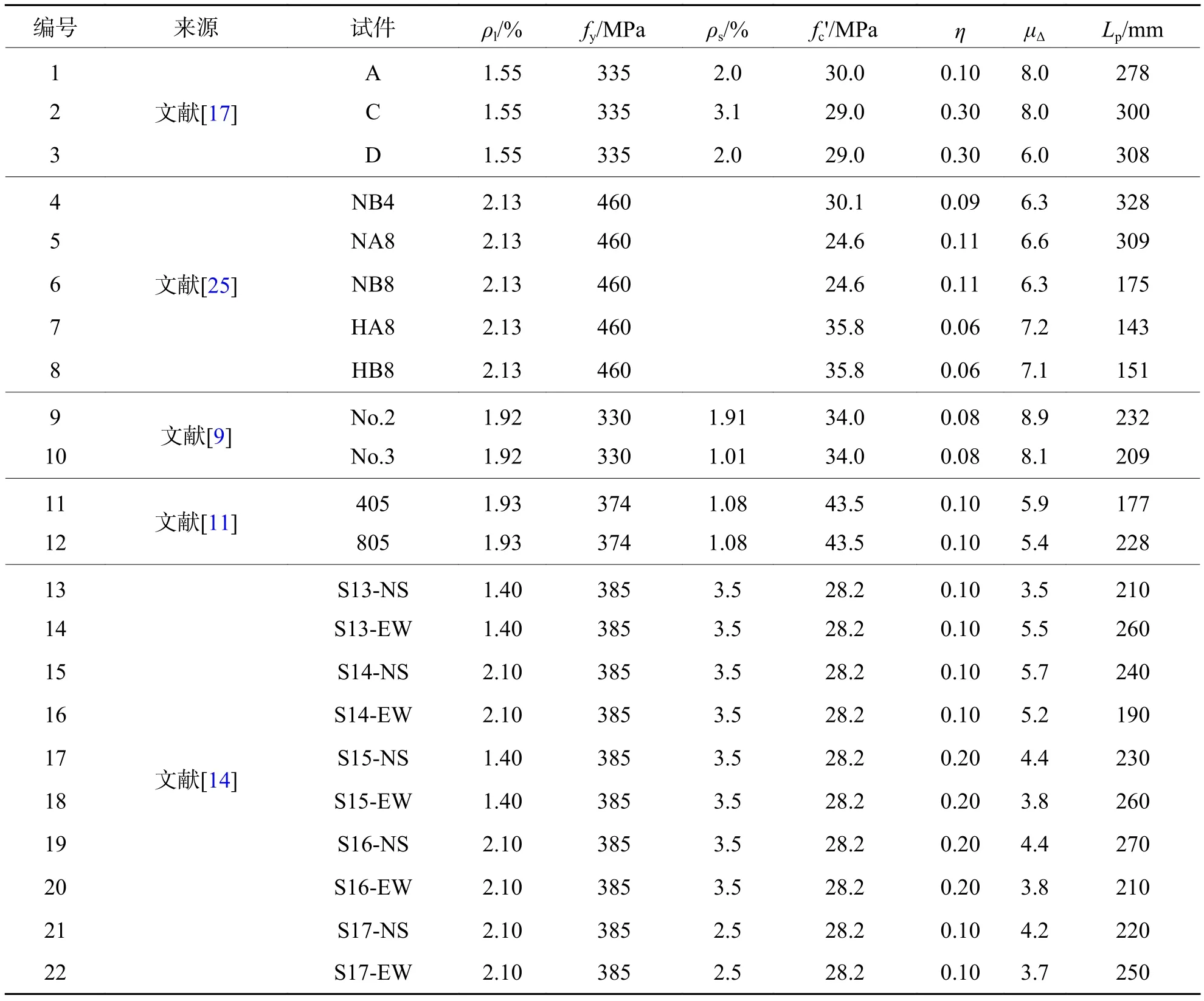
表4 文献中试件参数及LpTab.4 Parameters and Lp of specimens in literature

各参数对空心墩位移延性系数的影响如图8所示.位移延性系数随着轴压比（η）的提高而降低.为探讨剪跨比的影响，选取文献[9，14]及本文数据，其中Han等[14]的试验为双轴加载，由此可获取同一试件不同剪跨比对应的延性系数.由图8可见：剪跨比相对延性系数的变化规律不一，这主要源于剪跨比的增加对构件的屈服和极限位移均有明显提升，两者比值增减不能明确.根据不同η下纵筋率和配箍率的影响，发现当η在0.1附近时，纵筋的增加会适当降低延性系数，而η在0.05左右时，纵筋率的影响不大；当η在0.08～0.30时，加大箍筋用量可以提高延性系数，而轴压比0.05时的规律性则不强.鉴于目前大部分公式中均认为塑性铰长度随墩高增加而增大，而对其余影响因素取舍不一，因此利用表2和表4中试验数据分析名义塑性铰长度（Lp/h）随部分因素变化的影响.

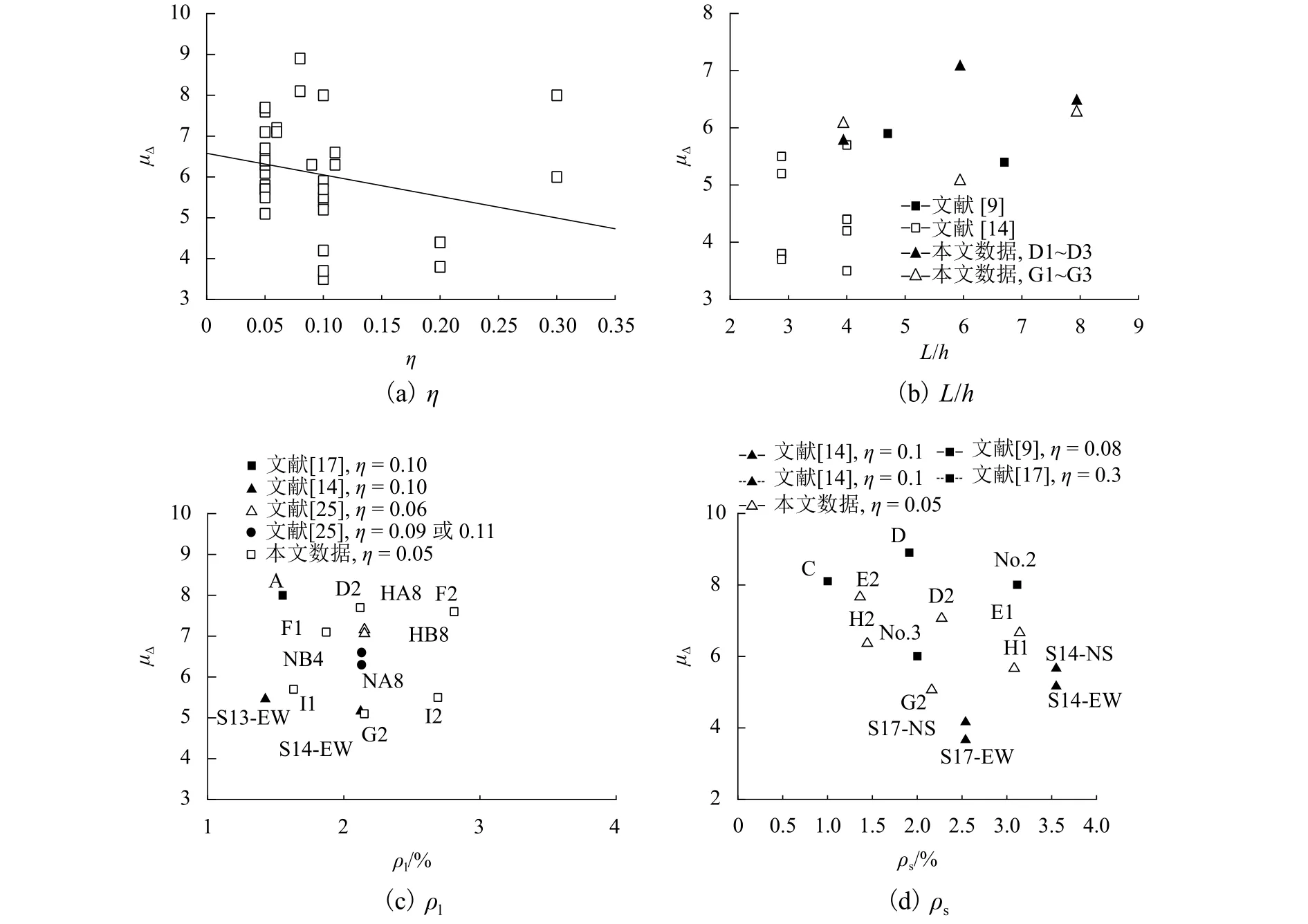
图8 各因素对空心墩位移延性系数的影响Fig.8 The effects of influencing factors on the displacement ductility factor of hollow piers

各因素对空心墩名义塑性铰长度的影响如图9所示.由图可见：随着轴压比和纵筋强度或直径的增加，空心墩的塑性铰长度有所扩大；随着混凝土强度的提升，空心墩塑性铰长度逐渐减小；配箍率变化的影响则不够显著.

图9 各因素对空心墩塑性铰长度的影响Fig.9 The effects of influencing factors on the plastic hinge length of hollow piers

4.3 评估结果分析

利用表3公式计算各试件等效塑性铰长度，并与实测值比较（m为塑性铰长度计算值与塑性铰长度试验值的比值），结果如图10所示.

图10 空心墩塑性铰长度计算值与试验值的比较Fig.10 Comparison between calculated and measured plastic hinge lengths for hollow columns

由图10可知：Watson-Park模型计算结果最大，其原因主要是该模型认为当几何尺寸确定后塑性铰长度仅随轴压比的增加而提高，由此可能会极大高估墩顶位移能力；Priestley-Park、Paulay-Priestley、Eurocode 8、《细则》等模型计算值已超过试验值的5%，高估了空心墩的等效塑性铰长度；Berry模型的预测结果略微保守，均值和变异系数分别为0.86和0.269；Mander、孙治国和JRA模型的计算结果与试验值误差不超过5%，与实测塑性铰长度较为接近，分别为1.05、1.01及1.03.

5 结 论

根据上述试验观测和数据分析，主要结论如下：

1）方形空心墩均发生了弯曲破坏，破坏集中在墩底塑性铰区域，各空心墩的μΔ在5.1～7.7，空心墩表现出较好的延性性能.

2）但相同剪跨比下空心墩侧面出现了较多斜裂缝，表明空心墩抗剪内力相对实心墩的更弱，需加强墩底塑性铰易损区域的构造设计.

3）增加纵向钢筋能够在一定程度上增强空心墩的侧向承载力和极限位移，但空心墩延性系数（η≥ 0.09）随着纵筋率的提高有所降低.

4）适当提高配箍率（η≥ 0.08）可以增强空心墩延性系数，但低轴压比下（η≤ 0.05），箍筋用量影响的规律性不强，这可能是低轴压比下箍筋对混凝土的约束效应不显著.

5）空心墩塑性铰长度随剪跨比、纵筋强度或直径、轴压比增加而提高，随混凝土强度增加而降低，配箍率的影响不大，与现有实心墩成果一致.

6）Priestley-Park、Paulay-Priestley、《细则》Eurocode 8等模型高估了空心墩塑性铰长度，会使得设计的桥墩偏于不安全性；Berry模型略微保守，从安全性出发可用于空心墩抗震初步设计.

7）Mander、孙治国和JRA模型所得的塑性铰长度和墩顶位移同实测值最为接近，其中Mander公式同时考虑了几何和材料特性，且变异系数最小，建议为空心墩塑性铰长度计算模型.

8）尽管通过拟静力加载可以详细观测空心墩损伤演化，评估极限位移能力，但高阶效应的存在使得空心高墩的震损模式与拟静力结果相比还是存在一定差异的.因此，大比例尺模型振动台试验和混合试验应是今后空心高墩研究的重要方向.