四模Lorenz-Stenflo系统动力学行为分析及其数值仿真
王贺元, 白 晨
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言
1963年,美国气象学家Lorenz[1]利用截谱方法,讨论了Rayleigh-Benard对流问题,得到了一个三维的非线性常微分方程组,也就是通常所说的Lorenz 系统。
随后,众多学者对Lorenz系统的各种特性展开了深入研究,揭示了该系统动力学行为的演化过程[2-6]及产生混沌的力学机制机理[7]。随着各种研究的不断深入,基于Lorenz系统,人们给出了丰富多样的修正模型,如四模类[8]、五模类[9-10]、九模类[11]等。
瑞典物理学家Lennart-Stenflo[12]发现,大气中低频短波重力扰动可以用4个广义Lorenz方程组来描述。当不考虑地球自转时,这些耦合方程简化为三模常规的Lorenz方程。这个低频和短波近似的大气方程即Lorenz-Stenflo模型:
(1)
其中:新增的状态变量x4描述了气流的旋转;新增的参数s是与x4相对应的旋转数(rotation number);q表示普朗特数(Prandtl number);r表示瑞利数(Rayleigh number);b表示几何参数(geometric parameter)。
在小旋转数s的情况下,随着r的变化,该系统的分岔结构和Lorenz系统是相近的[13]。若将旋转数s视为分岔参数,那么随着s的变化,该系统的分岔结构便与一维逻辑斯蒂映射非常相似[14]。
1 Lorenz-Stenflo系统的吸引子和稳定性
多数非线性微分方程很难求出其解的具体表达式,因此,在不具体解出方程的情况下,判断方程的解的稳定性态以及解的性态就显得尤为重要。从物理意义方面考虑非线性微分方程的解的稳定性同样具有现实意义[15]。
1.1 平衡点

1.2 零点的线性稳定性
在零点附近做线性近似,得到一个四阶矩阵,该四阶矩阵有特征值方程:
(λ+b)[λ3+(2q+1)λ2+(q2+2q-rq+s)λ+(q2-q2r+s)]=0
由劳斯赫尔维茨稳定性判据,满足下列条件时,方程只有负实部的解:
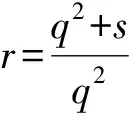
1.3 对称点的线性稳定性
作平衡点附近的代换xi=pi+Xi(i=1,2,3,4),根据劳斯赫尔维茨稳定性判据,其性质与原点的稳定性基本相同。
1.4 全局吸引子存在性分析

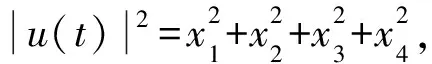
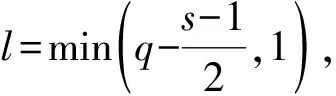
由Gronwall不等式得

1.5 全局稳定性
借助李雅普诺夫函数法,讨论系统(1)的全局稳定性。构造李雅普诺夫函数:
显然,当K是常数时,上式表示一个四维椭球面,把这个椭球面所包围的单连通区域记做H,K越大,椭球面越大。求V的导数:
显然,下式可以视为一个四维椭球面,记为U,则
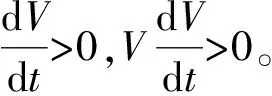
2 数值仿真
由文献[16]可知,参数取q=10,s=30,b=8/3符合物理含义,在这几个取值条件下对Lorenz-Stenflo系统的动力学行为进行数值仿真。
2.1 最大李雅普诺夫指数
李雅普诺夫指数是衡量系统动力学特性的一个重要的定量指标,正的李雅普诺夫指数意味着,无论2条轨线的初始间距多么小,其差别都会随着时间的演化而成指数率增加,以至于无法预测,这就是混沌现象。图1为瑞利数从0~600变化时的最大李雅普诺夫指数。

图1 最大李雅普诺夫指数
2.2 分岔图
状态变量和分岔参数构成的二维图形表示状态变量随分岔参数变化的规律。通过分岔图可以得到系统响应的周期运动或者拟周期运动以及混沌运动所对应的参数区间,在一定程度上可以用于判定通向混沌的道路。图2为瑞利数从0~600变化时的分岔图。2个图像对比可见,最大李雅普诺夫指数越大,分岔图对应的系统混沌程度越大。

图2 分岔图
2.3 吸引子
空间中每一点都表示系统在某一时刻的状态,当状态发生变化时,相空间的点移动进而构成轨迹,在轨迹上的点的不变集则为吸引子。周期振荡的吸引子为一条封闭的曲线,也就是极限环。准周期震荡则为轮胎型的曲面。混沌吸引子的轨迹具有局部不稳定性、整体有限性和结构自相似性等特点。以洛伦兹方程为例,其吸引子轨迹类似于蝴蝶,如图3和图4所示。
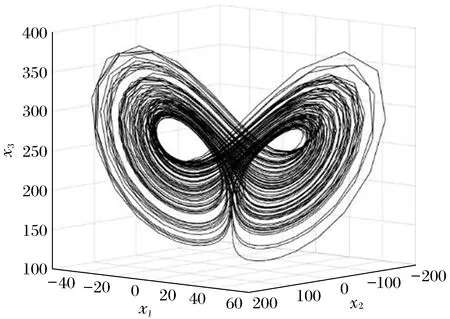
图3 r=280吸引子
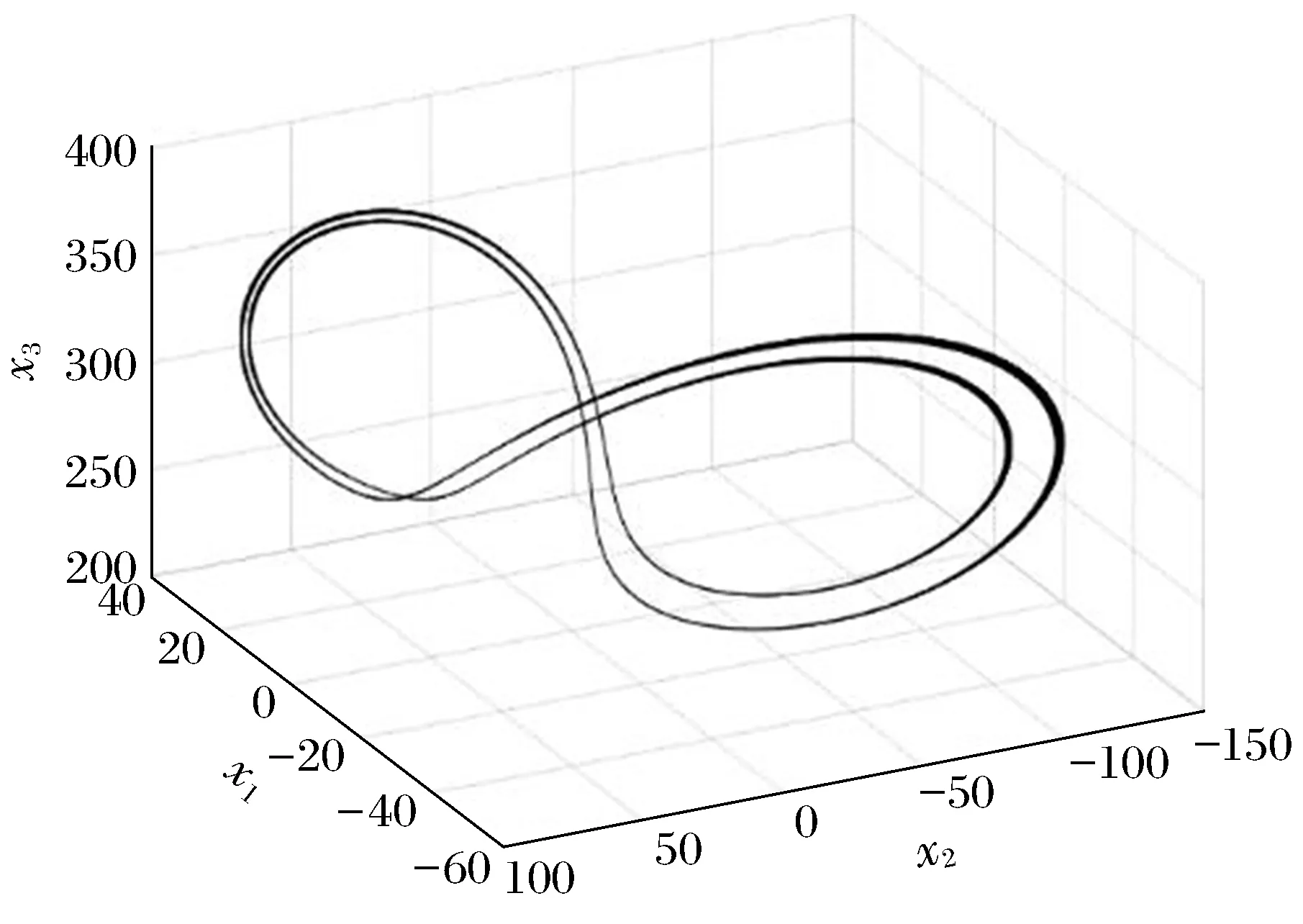
图4 r=300吸引子
2.4 庞加莱截面
维数比相空间少的低维截面与吸引子相截得到庞加莱截面。庞加莱截面法就是把连续的轨线变为离散的点,进而研究运动的特征和变化规律。图5为瑞利数取248时x1与x2的庞加莱截面,由图5可知,系统处在混沌状态,截面与洛伦兹系统的蝴蝶形状相似。
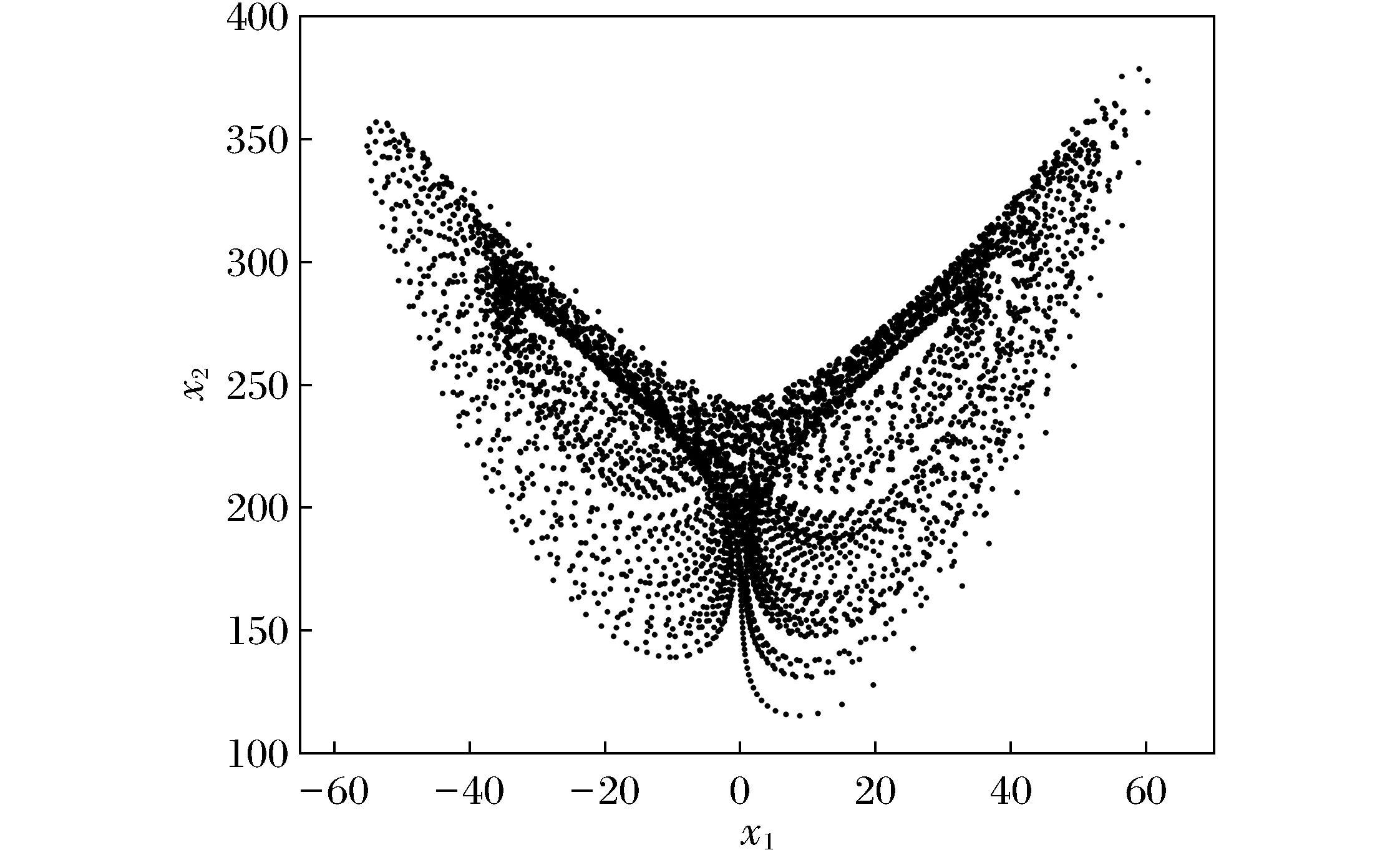
图5 庞加莱截面
2.5 时间序列
用数值方法将方程的解随时间变化的过程描述出来,也就是混沌运动的时间过程,以直观清楚地反映系统响应随时间变化的规律。图6为瑞利数取248时x1与时间t的时间序列,由图6可以看出,系统的解并不是简单的周期解,而是非周期的、复杂的、混沌的。
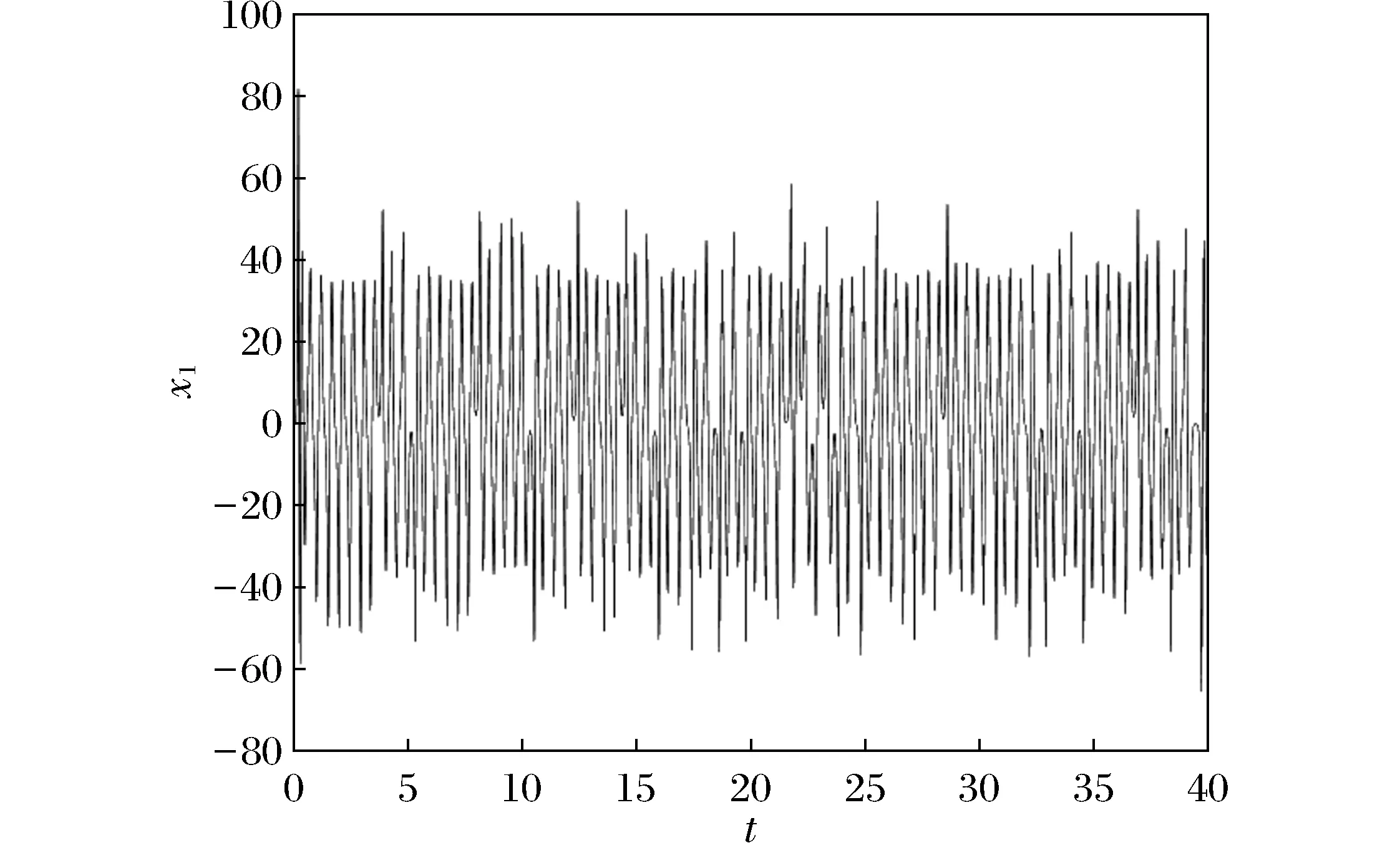
图6 时间序列
3 结 论
通过对Lorenz-Stenflo系统的数值运算,得到该系统的平衡点及局部和全局稳定性等性质。通过对Lorenz-Stenflo系统的数值仿真,发现其三维图像经历了奇怪吸引子、拟周期轨道、极限环等形状,系统存在复杂的窗口期和倒分岔过程。综上所述,在考虑气流旋转因素这一前提下,随着瑞利数的增加,该系统的动力学行为的变化更为复杂。

