图像模糊聚类分割初始聚类中心优化算法研究

范浩祥，张小凤

(陕西师范大学物理学与信息技术学院，陕西 西安 710119)

1 引言

图像的分类与识别在智能信息领域中具有广泛的应用[1]。在图像处理中，图像分割是至关重要的技术[2]。通常的图像分割方法主要有阈值分割、聚类分割、边缘分割等[3]。其中聚类分割方法中，模糊C均值算法(Fuzzy C-Means： FCM) 是一种无监督的聚类分割算法[4]，广泛应用于医学图像、遥感图像和红外图像分割[5]等多个方面。

FCM作为一类通过迭代更新使目标函数逼近最优值的算法，其存在着对初始值敏感和易于陷入局部最优的问题。目前，对FCM算法在图像处理应用中的改进主要包括：聚类数量的自适应确定、聚类中心初始化、利用图像空间信息提升算法有效性等。在聚类中心初始化方面，单凯晶[6]等采用一种改进的最大最小距离算法对原始空间中的数据进行粗分类，所得结果作为初始聚类中心。万龙[7]提出均值距离最远中心法。刘万军[8]等人使用灰度直方图波峰和波谷寻找初始聚类中心和聚类数。马冬梅[5]等人通过灰度直方图的斜率来确定聚类数量和初始聚类中心。虽然对灰度统计直方图分布形态的分析，可以充分利用图像的灰度信息，但不可避免的在某些灰度直方图中存在宽度极小的尖峰，导致依照形态学来分析灰度直方图时出现较大误差。Yager[9]等人提出了山函数算法用以解决FCM中聚类中心初始化的问题，用以实现聚类中心点和聚类数量的自适应确定。Chiu[10]在山函数基础上提出减法聚类，以样本点来计算候选聚类中心，减少了工作量。裴继红[11]等人提出了样本空间中样本半径的计算方法，并应用密度函数算法来确定聚类中心，使算法计算复杂度大幅度降低。该算法在初始聚类中心的确定、聚类效果以及抗噪性方面都有着良好的效果。以上文献中部分使用了密度分布特征，可以在一定程度上使得初始聚类中心点的分布更趋合理，降低了FCM算法陷入局部最优的概率。

在实际应用中，FCM的聚类中心和隶属度矩阵在算法中是相互依赖的。在算法执行过程中，其中一方有较大数值调整会导致另一方有大幅度的变动。而传统FCM算法中，聚类中心及隶属度矩阵的初始化值与最终聚类结果有一定差别，FCM算法在执行的起始若干代中，聚类中心出现较大幅度的调整，即粗聚类阶段。在算法迭代一定代数后，聚类中心逼近最优结果，聚类中心的变化趋于小范围调整收敛，即为细聚类阶段。通常，在对FCM进行初始化参数优化改进时，会优先选择优化初始聚类中心点的位置分布，而隶属度矩阵在算法开始时依然是随机初始化。因此，单纯对聚类中心点位置初始化的算法只是在一定程度上减少了FCM算法在粗聚类阶段的时间消耗。

针对上述问题，本文提出了灰度直方图区域中位点法，该算法结合直方图灰度合并谷值寻优确定聚类数量，通过均匀划分灰度级别区域并计算其像素数量中位点来确定待分割图像的初始聚类中心，实现图像的聚类中心初始化。将灰度直方图区域中位点法和FCM算法相结合，实现对图像聚类分割性能的提升。

2 相关工作

2.1 FCM

1981年，J.C.Bezdek[12]等人将已有的K-means硬聚类算法推广为模糊C均值聚类算法，即FCM算法。

设X={xi|i=1，2，…，N}是有N个数据、K个类的数据集，在FCM算法中，通过优化如下的目标函数来实现聚类

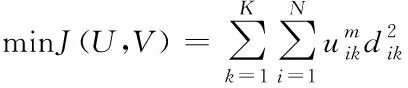
(1)

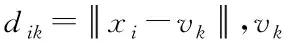
(2)

模糊隶属度和聚类中心的迭代公式如下

(3)

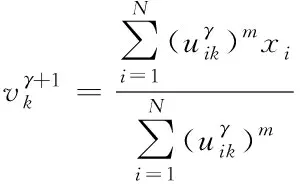
(4)

其中γ为迭代代数。

FCM算法在应用到图像分割中时，主要是灰度图像的分割。由于灰度图像灰度等级的有限可数特性，在完成模糊聚类过程后，还要对聚类中心进行取整，对各个灰度级的隶属度进行硬化。

2.2 灰度图像映射到直方图空间

假设图像的大小为S×T，f(s，t)是图像阵列在位置(s，t)处的像素灰度值函数，f(s，t)∈{0，1，2，…，255}。定义图像的一维灰度统计直方图函数为

(5)

其中

(6)

则传统FCM算法的目标函数可表示为

(7)

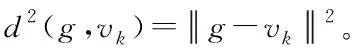
(8)

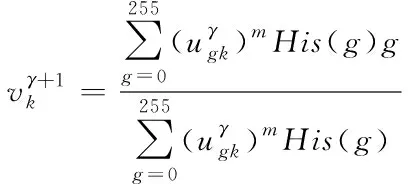
(9)

将图像从原像素空间映射到其灰度直方图特征空间，由于灰度直方图最大只有256个灰度级别，在一定程度上限制了算法中需要处理的数据量大小，因而使用这种映射关系的算法，相较于传统FCM算法可提高图像分割的效率[13]。

3 基于区域中位点的聚类中心初始化方法

通常，图像的灰度统计直方图中“峰”的数量与图像的最优分割数量存在某种关联。在对图像的灰度直方图进行划分的过程中，将若干灰度级合并可减少灰度直方图中的“毛刺”，方便获得灰度统计直方图中的“谷”，进而确定聚类数量。基于此，本文将原256个灰度级均分为32组，将原灰度直方图His(g)，g∈[0，255]，映射为新的灰度直方图H′(g′)，g′∈[1，32]，采用以“谷”来划分“峰”的方法，通过确定合适的“谷”的数量，保证灰度直方图H′(g′)中每个大“峰”都能在一个独立区间内，在一定程度上降低形态学分析带来的聚类数量的误判。

在预选出候选“谷”点的过程中，需要解决两个问题，其一，由于直方图的分布特点，在用“谷”点确定区间分割数量时，由于两“谷”点距离过近或“谷”点距离灰度空间边界过近导致出现极小区间。其二，直方图的边界出现低密度分布区域会导致低密度分区。

对于第一个问题，在预选出候选“谷”点后，用现有候选“谷”点对整个灰度空间进行分割，取各分割区间宽度的均值的一半作为阈值φ，当现有分割区间的宽度小于φ时，则将该区间与其左侧区间合并，若区间左侧为灰度空间边界，则将该区间与其右侧区间合并。

对于第二个问题，假设图像的大小为S×T，当同时满足如下两个条件则该区域为低密度分布区域：

条件1：灰度直方图H′(g′)中单个灰度级像素数量不及图片总像素数量的0.1%，即单灰度级像素数量阈值

βs=(S×T)×0.1%

(10)

条件2：从灰度空间边界起连续多个灰度级对应像素数之和不及总像素数的0.5%，即连续多灰度级像素总数阈值：

βm=5βs

(11)

Lena图像的灰度直方图低密度分布区域示意图如图1。由图可知，Lena图像灰度直方图的两端，单个灰度级不超过50像素，从边界起连续灰度级像素数量和不超过250，则该区域为低密度分布区域。

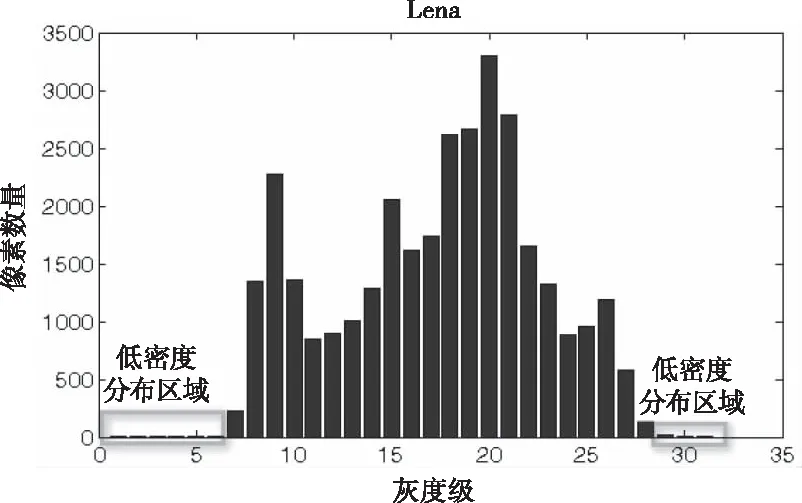
图1 灰度直方图低密度分布区域示意图

在明确了灰度直方图中“谷”的确定方法后，考虑采用直方图灰度合并谷值寻优确定聚类数量，通过划分灰度级别区域，计算直方图的像素数量中位点来确定待分割图像的初始聚类中心。算法流程图如图2所示。

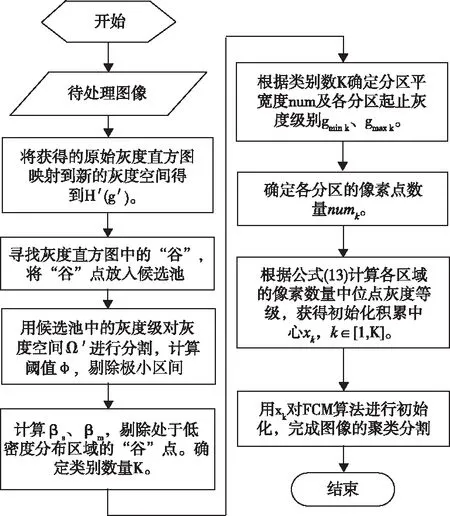
图2 区域中位点聚类中心初始化FCM算法流程图

具体流程如下：

Step1：获取灰度图像的灰度统计直方图His(g)，将256个灰度级别均分为32组，每一组包含8个灰度级别，即将原灰度空间Ω映射为新灰度空间Ω′，获得新灰度直方图函数H′(g′)，g′∈[1，32]。

Step2：在H′(g′)中，当一个灰度级的对应像素数量小于左右相邻两个灰度级别对应的像素数，确定其为“谷”，将该灰度级放入候选池。

Step3：用候选池中的灰度级对灰度空间Ω′进行分割。计算阈值φ，当区间的宽度小于φ，则将该区间的左边界(较小的灰度级)从候选池中删除，若区间左边界灰度级为1，则将该区间的右边界(较大的灰度级)从候选池中删除。

Step4：计算得出当前待处理图像的单灰度级像素数量阈值βs和连续多灰度级像素总数阈值βm。当处于灰度直方图两端的灰度级同时满足条件1和条件2，则该区域为低密度分布区域。

若有候选“谷”点在此区域，需将其从候选池中删除。此时候选池中剩余的“谷”点数量加1，即为算法确定的聚类数量K。

Step5：获取图片的总像素数N，以K为聚类数进行像素数量均分，各分区像素数量均值为num=N/K。根据num确定灰度空间Ω中各类别的起止灰度级别gmink、gmaxk，k∈[1，K]，对His(g)进行分区。

Step6：由step5获得直方图分区，计算每个分区包含的像素点数量分别为numk，其中

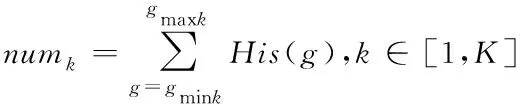
(12)

Step7：根据式(13)计算各区域的像素数量中位数所在灰度等级，即FCM初始化中心点xk

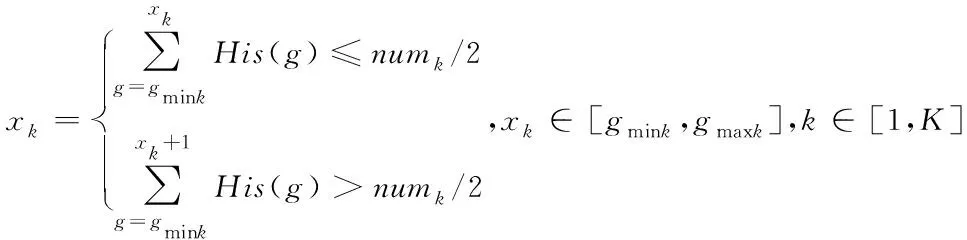
(13)

4 实验结果与分析

为验证区域中位点法在图像聚类分割初始化阶段的效果，分别采用Lena图像和BSDS500数据集中的图片对算法的性能进行测试。在CPU为AMD Ryzen5 2500U 2.00 GHz，内存8GB，Windows10 64位系统，Matlab 2014a编程环境下，对测试图像分别采用区域中位点法、最大最小值法和减法聚类法方法进行聚类分割初始化。在仿真测试过程中，每张测试图片分别使用每种算法执行30次，取运算平均用时进行比较。

首先，用Lena来验证区域中位点法算法的性能。实验所用Lena图片及其灰度直方图如图3-a1，3-a2所示。图3-a3为用不同初始化方法进行初始化时的目标函数变化曲线。由图3-a3的结果可知，本文算法具有较快的收敛速度，可以用较少的迭代次数，实现图像的初始化。不同初始化方法所获得的Lena图像的聚类中心结果如表1所示。由表1中Lena图像的结果可见，减法聚类和区域中位点法均可以找出Lena图片的聚类中心数为4个，聚类数量与文献[14]Lena图像四聚类的结果一致，且区域中位点法获得的初始化中心与FCM算法的结果更加接近。

选用BSDS500数据集中编号为87015、181079、223061、230098、385028的图片，对区域中位点法的图像分割性能进行了测试，其原灰度图、灰度直方图和聚类分割目标测试，如图3b-f所示。其中，图3的b2～f2为测试图片的灰度直方图，b3～f3为算法初始化后FCM聚类分割目标函数变化曲线。可以看出，应用不同初始化方法获得的聚类中心应用到FCM算法后，获得的目标函数值均收敛到相同值。图3-a3～f3中，区域中位点法均以显著优势收敛到最优值，且区域中点法初始化的目标函数最终收敛值明显小于其它初始化方法。即，相较于对比算法，本文算法对FCM算的加速效果更为显著。

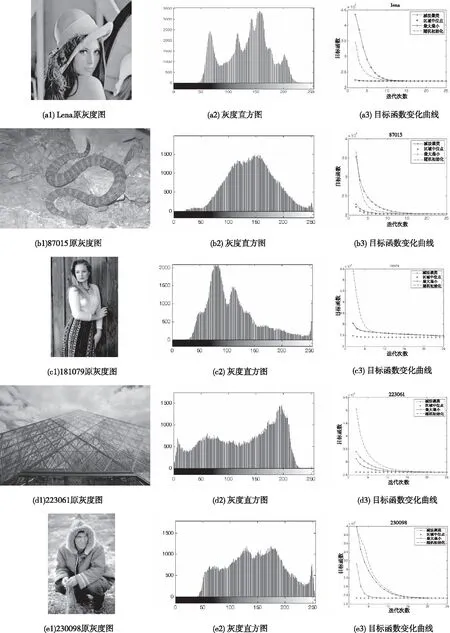
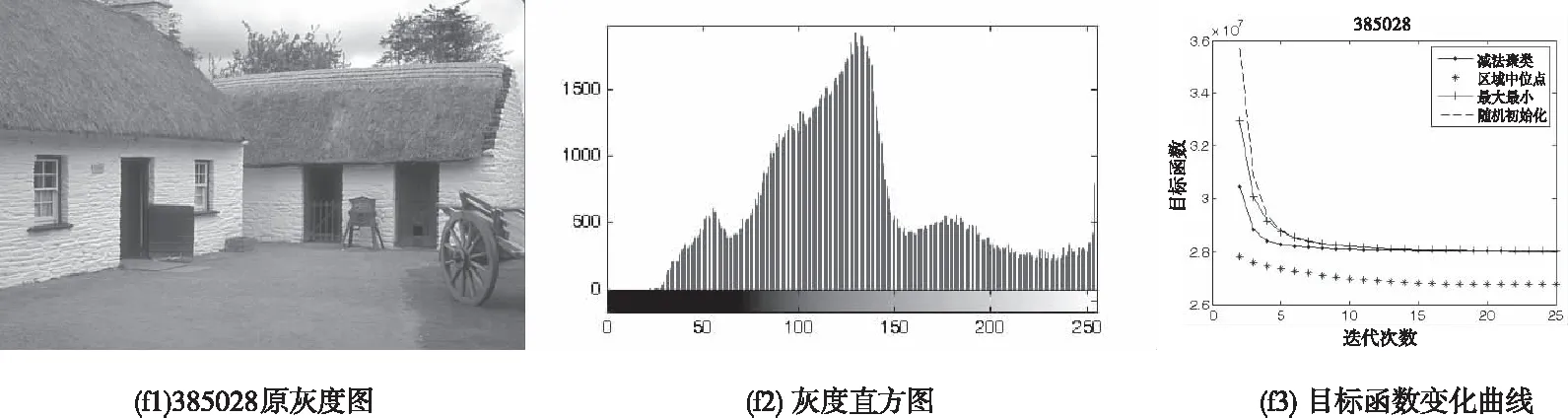
图3 测试图片及其对应的灰度直方图和目标函数变化曲线

表1所示为不同方法初始化得到的聚类中心与FCM获得的聚类中心的对比。从表1中可以看出，四聚类的情况下，本文所提出的初始化算法获得的聚类中心点与FCM最终聚类结果非常接近，比如，在编号为223061的测试图例中，区域中位点法得到的初始聚类中心到最终结果平均距离为3，而减法聚类除第四个中心与结果很接近外，初始化中心与最终结果距离均值为17.75，减法聚类的结果与FCM的聚类结果差异较大。

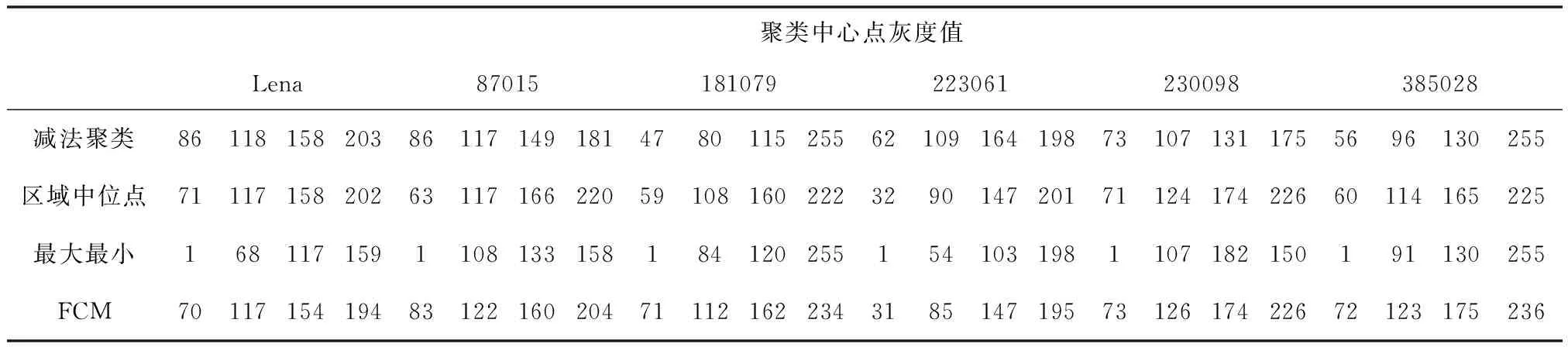
表1 不同初始化方法获得的聚类中心与FCM聚类结果的对比

为了探究算法的执行效率，将初始化阶段的耗时用T1表示，FCM算法阶段耗时用T2表示，用T2-FCM表示传统FCM算法的平均耗时，总耗时为Ttotal=T1+T2，Ttotal-FCM表示传统FCM算法平均总耗时，并设Ttotal-FCM=T2-FCM，分别从算法总耗时，初始化后FCM阶段算法耗时两个方面呈现算法特性。为了表征不同初始化FCM算法相较于传统FCM算法的执行效率，定义

(14)

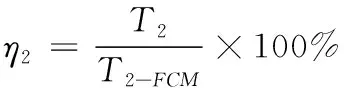
(15)

仿真结果如表2和表3所示，其中表2为优化总耗时与随机初始化FCM的耗时对比，表3为优化初始化后，FCM阶段耗时与随机初始化FCM耗时的对比。从表2和表3的计算结果可以看出，三种初始化方法均一定程度上降低了FCM聚类算法在时间上的消耗，对于图87015、181079、230098，本文算法的执行效率相较于传统FCM均有13%～25%的提升，而在对于图385028的结果，区域中位点法更是实现了超过一倍的性能提升。区域中位点法在FCM阶段运行时间的消耗与初始化加FCM阶段运行时间消耗方面，均低于随机初始化情况下FCM平均运行时间的一半。

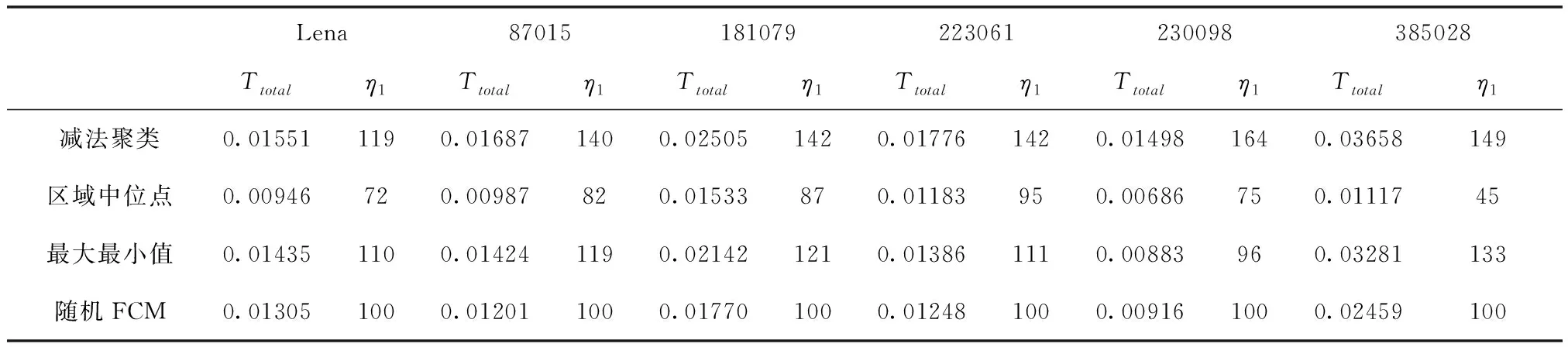
表2 Ttotal (s)耗时对比

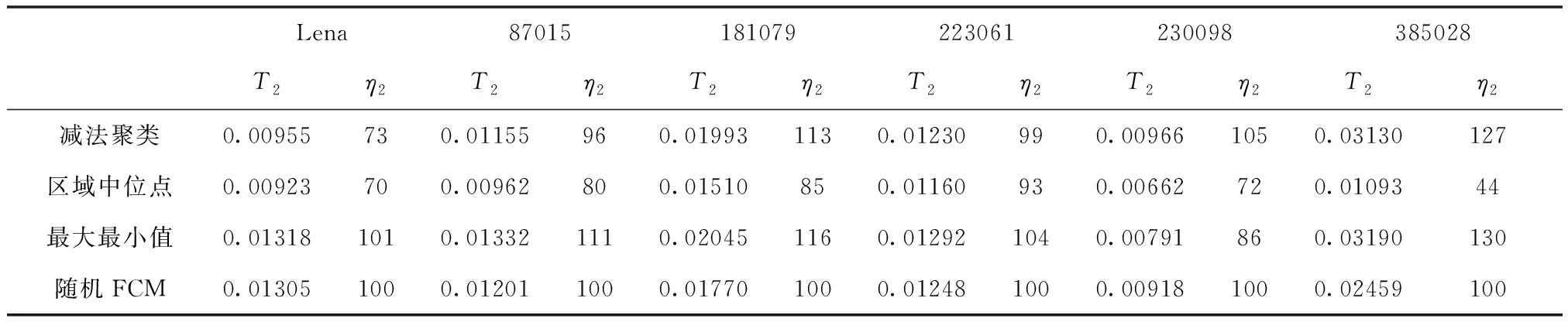
表3 T2(s)耗时对比

5 结语

针对现有FCM图像聚类分割算法聚类中心随机初始化易导致算法陷入局部最优且计算效率不高的问题，提出了一种基于图像灰度直方图灰度级合并谷值寻优确定聚类数量，并依据图像灰度统计直方图的均分区域中位点确定FCM聚类初始化中心点。对实际的图像进行FCM聚类分割的结果表明，相较于对比算法，本文算法在运算复杂度和对FCM算法的加速方面具有较为明显的优势。