动热源摆式双轴MEMS 热加速度计敏感机理的研究

朴林华,佟嘉程,李备,张严

(北京信息科技大学 北京市传感器重点实验室,北京 100101)

现如今,市场对微型加速度计适应恶劣苛刻的环境能力要求越来越高,因此,MEMS(Micro-Electro-Mechaniacl System)热气体加速度计以其超高抗冲击能力和超低制造成本在微机械传感器中独树一帜,其他固体摆式MEMS 加速度计无法与之媲美[1-2]。微机械热气体加速度计用热气体质量块代替传统的固体质量块[3],敏感质量几乎为零,其优秀的抗冲击性能在很多文献中都得到了验证[4],同时它结构简单、体积小、重量轻、成本低,是理想的中低精度惯性器件,在导航、汽车电子、无人机、可穿戴电子设备等领域有广阔的应用前景[5-7]。2017 年Han 团队提出了一种单轴热对流加速度计[8],为了提高加速度计的灵敏度和频率响应,该团队优化了加热功率、空腔尺寸、气体介质和空气压力等参数。同年印度理工学院提出了一种改进双轴热加速度计[9],通过设置硅岛调节腔体中的温度分布,提高灵敏度。2019 年,香港科技大学提出了一种科氏力补偿型双轴微热对流加速度计(CMTCA)[10],实现了一种低耦合效应的双轴微热对流加速度计。2018 年,日本京都立命馆大学提出了一种带闭环热源的三轴热对流加速度计[11],实现了三轴测量。MEMS 热气体加速度计的基本工作原理是利用加热器(热源)产生的热流在输入线加速度作用下发生移动,产生不对称温度场,通过设置对称的热线(热敏电阻)检测温度场的不对称分布。与传统的固体摆式加速度计相比,微机械热气体加速度计的灵敏度相对较低,主要原因是热气体的等效质量和运动速度均小于固体质量块。由于热气流速度很小,气流偏转时造成的不对称温度场梯度很小,因此由热敏电阻构成的惠斯登电桥输出的不平衡电压小,加速度计的灵敏度低。因此,提高MEMS 热气体加速度计的灵敏度是亟待突破的关键技术之一。在现有的解决方案中,虽然可以通过加大加热器功率的方法提高灵敏度,但是受到功耗的限制,灵敏度没有实质性的改变和提高。为了突破这个难题,本文打破以往对热气体加速度计研究的固有模式,提出一种新型的动热源摆式双轴MEMS 热加速度计,使热源(加热器)产生移动,由于热源——硅的导热系数远大于气体的导热系数,硅制热源的存在会调节腔体中的温度分布,让它受到惯性力的作用发生摆动,在热线处形成大的温度梯度,从而实现大灵敏度的输出。本文提出的这种加速度计能独立测量两个正交敏感轴方向(X、Y)的加速度,由于采用光刻技术能保证敏感结构的正交性和垂直度,因此加速度计在轴向准确性和交叉灵敏度上比由两个单轴加速度计组成的二轴加速度测量系统更有优势,交叉耦合小,同时可以消除由单轴陀螺组合安装距离产生的测量误差。由于MEMS 传感器制作流片成本高,对于研发新型MEMS 传感器,在制作流片之前对传感器工作机理方面进行理论研究,对于传感器性能的预判至关重要,是该传感器研发可行性的重要依据。本文在介绍该热气体加速度计结构原理的基础上,根据控制方程和加速度计的实际几何结构,利用有限元计算方法对这种双轴加速度计的输入-输出关系进行了定量计算验证,从而揭示该双轴加速度计的敏感机理。

1 结构原理

动热源摆式双轴MEMS 热加速度计主要包括盖板、敏感层。敏感层上的盖板使敏感层的上表面处于密闭腔体里,敏感层结构如图1 和图2 所示。敏感层是由MEMS 体硅工艺制作的硅板,在硅板的上表面有一悬空的动热源H(加热器),在其周围两个相互正交的敏感方向(X方向和Y方向)分别设置两对对称平行、悬空的热线TX1和TX2、TY1和TY2。动热源和热线结构组成部分相同,均由硅和高温度系数的金属组成,两端都镀有金属电极。动热源H 是一种可动式热源,是一种电阻加热器,它采用风火轮式摆式结构,中心轮轱是一个圆形的质量块,圆形的质量块通过八个完全对称的半圆形辐条(也叫支撑梁)悬置在敏感层的中心位置,H 的下方是圆形的凹槽,热线TX1和TX2、热线TY1和TY2下方是与上述圆形凹槽相同深度的长方形凹槽。动热源H 除了能沿着垂直于敏感层平面的Z轴上下振动外,它在敏感层XOY平面上任一方位角上都有惯性力的自由度(因此可以叫做全方位摆),能够敏感在XOY平面任一方位角上的输入加速度。

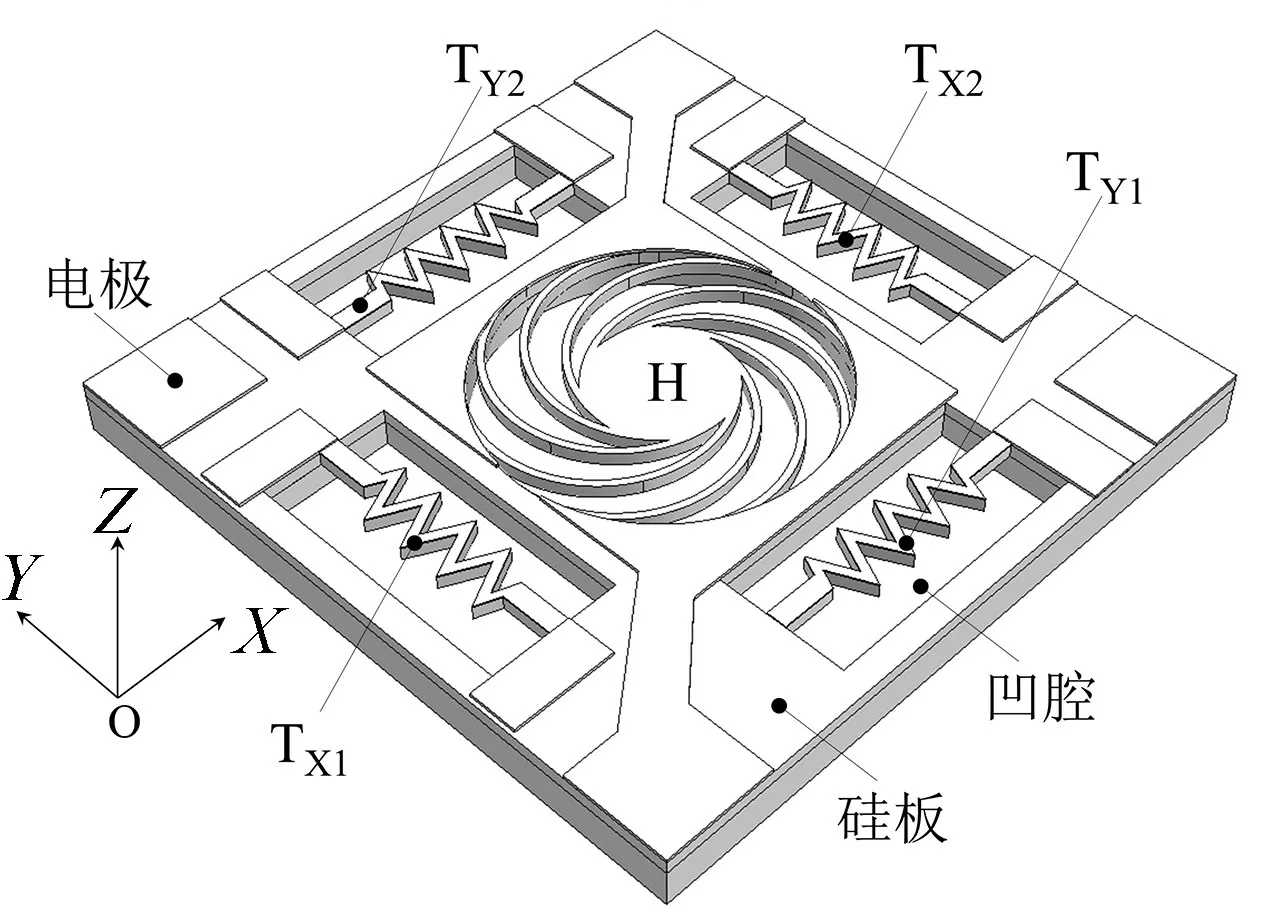
图1 热气体双轴加速度计结构示意图Fig.1 Structure diagram of hot gas biaxial accelerometer

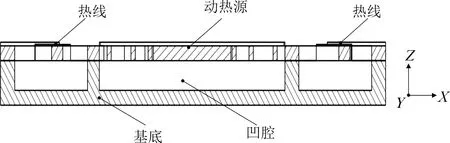
图2 双轴加速度计敏感层剖面图Fig.2 Sensitive layer profile of biaxial accelerometer

动热源摆式双轴MEMS 热加速度计的工作原理如图3 所示。给动热源H 摆通一恒定的电流,产生焦耳热,向周围气体释放热量,进行热扩散,在其四周形成热流。在无加速度输入时,热流产生的温度场相对X、Y方向的热线对称分布,热线TX1(TY1)和TX2(TY2)的温度相同,两个热线的温差是零。当沿着X轴(Y轴)正方向输入线性加速度时,动热源摆在加速度的作用下沿着与加速度方向相同偏移,造成热气流产生的温度场在密闭腔体内不再对称分布,同一方向的两个热线TX1(TY1)和TX2(TY2)温度变化相反,动热源摆偏向的热线TX2(TY2)温度高于和它平行对称的热线TX1(TY1)温度。两对热线温度差可以表示为:

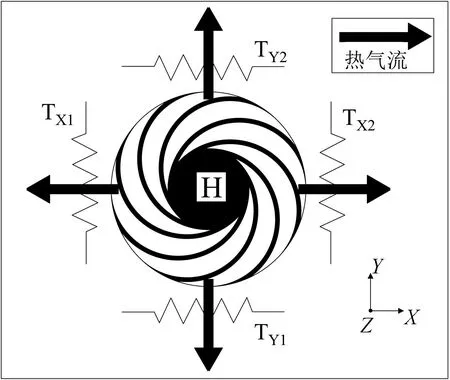
图3 双轴加速度计工作原理图Fig.3 Working principle diagram of biaxial accelerometer

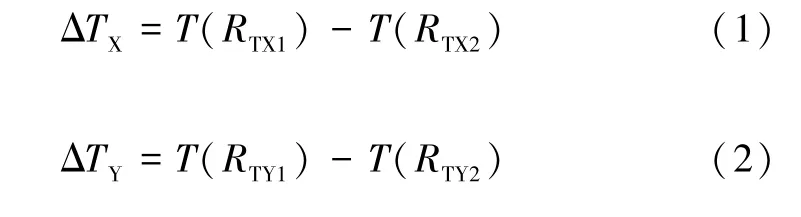
式中:T(RTX1)和T(RTX2)分别是热线TX1和TX2的温度值;T(RTY1)和T(RTY2)分别是热线TY1和TY2的温度值;RTX1和RTX2分别是两热线TX1和TX2的电阻值;RTY1和RTY2分别是两热线TY1和TY2的电阻值。将TX1(TY1)、TX2(TY2)和两个等值的平衡电阻(R)组成两个惠斯登电桥,如图4 所示,该电桥为双轴加速度计的提取电路。当输入线加速度引起温差时,根据热阻效应,将温差转化为桥臂电阻的变化,从而引起与输入加速度成正比的电桥不平衡电压VXOUT(VYOUT),其表达式分别为:

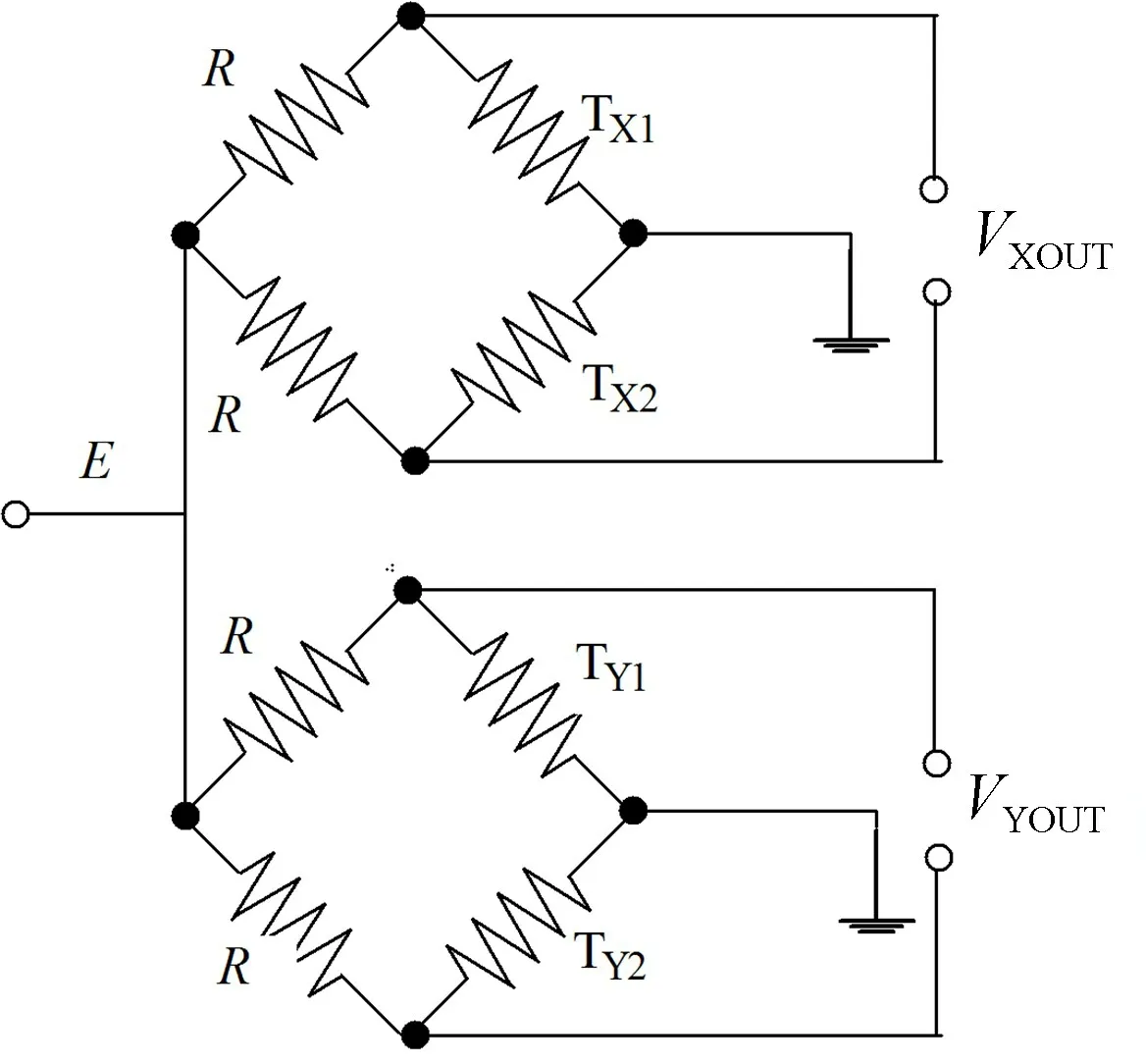
图4 双轴加速度计提取电路Fig.4 Extraction circuit of biaxial accelerometer

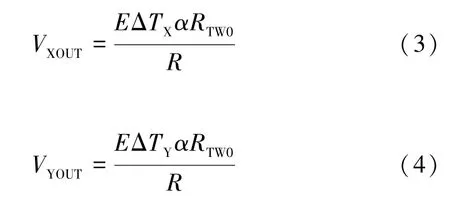
式中:E是加在电桥两端的直流电压;R是电桥平衡电阻的阻值;RTW0是热线的初始电阻;α是热线的电阻温度系数。由式(3)、(4)可见,如果温差ΔTX(ΔTY)为零,VXOUT=0,VYOUT=0,输入的加速度就是零。如果温差ΔTX＞0 (ΔTY＞0),则VXOUT＞0 (VYOUT＞0),加速度的方向与X(Y)轴一致;如果温差ΔTX＜0(ΔTY＜0),则VXOUT＜0 (VYOUT＜0),加速度的方向与X(Y)轴相反。VXOUT(VYOUT)正比于输入加速度引起的温差ΔTX(ΔTY),因此根据输出电压的大小和正负,可以判断X、Y轴输入线加速度的大小和方向,从而构成一个动热源摆式双轴MEMS 热加速度计。

2 二维研究模型

由于动热源摆式双轴MEMS 热加速度计敏感结构具有轴对称性,且热源和热线均在同一个XOY平面内,热源产生的温度场在密闭腔体均匀分布,所以为了便于建模和计算,可以考虑一个包含热源和两对正交热线并垂直于对称轴的一个二维X-Y平面,如图5所示,这个二维加速度物理模型作为有限元研究对象,计算其内部温度场的分布。

图5 双轴加速度计二维物理模型Fig.5 Two-dimensional physical model of biaxial accelerometer

3 有限元法求解

从本文提出的双轴加速度计工作原理可以看出,敏感机理涉及固体和气体的传热、固体运动学和动力学以及流固耦合等多物理场耦合。本文采用有限元多物理场计算软件COMSOL 对传感器内部物理作用机制进行计算。密闭腔体内的热源移动、传热和惯性力的加载等物理作用机制主要由传热方程、气体流动的纳维-斯托克斯方程、多物理场耦合的连续性方程等控制:

(1)传热方程。

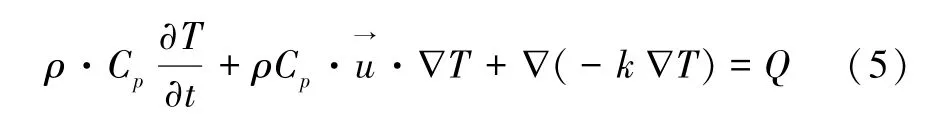
式中:ρ(kg/m3)为气体密度;Cp[J/(kg·K)]为定压比热容;k[W/(m·K)]为导热系数;为气体流动速度;Q(J)为热源产生的热流。

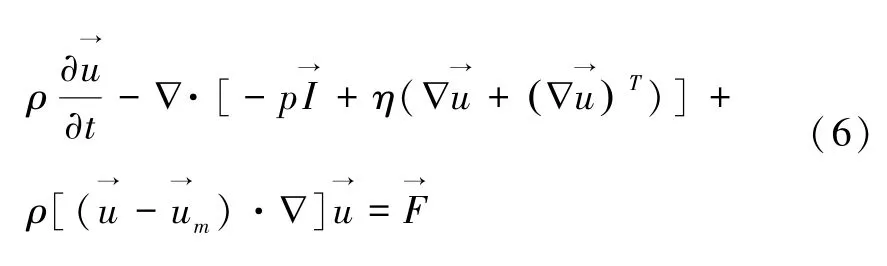
式中:为单位对角矩阵;为作用在气体上的体积力;η(Pa·s)为动力粘度。

(3)多物理场耦合。非等温流动和共轭传热界面的可压缩的连续性方程:

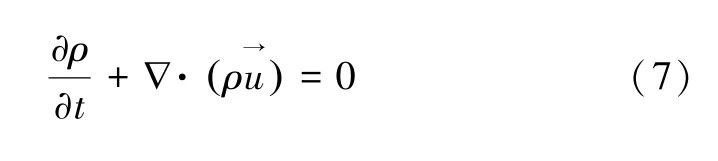
有限元计算的步骤包括以下几个方面:

(1)建模。根据所述的简化物理模型,建立双轴加速度计二维有限元模型,如图6 所示。给动热源通以电压5 V 形成恒定电流,产生焦耳热作为热源发热,研究方式设置为瞬态;

(2)设置参数。根据实际结构的材料组成部分,设置热线和热源以及气体的材料参数;

(3)物理场的设置[12-13]。这是温度场计算的关键,根据本文提出的热加速度计内部物理作用机制,包含惯性力作用固体运动-固体发热-固体与气体的相互作用等物理过程,开启电流、固体与气体传热、层流、固体力学等物理场以及流固耦合、电磁热和热电效应多物理场耦合。根据热源运动的特点,开启动网格分量设置;

(4)网格的划分。采用物理场控制划分网格,单元大小采用网格细化,以满足对计算精度的要求,划分网格后的示意图如图6 所示;

图6 双轴加速度计二维有限元模型Fig.6 Two-dimensional finite element model of biaxial accelerometer

(5)求解。采用全耦合求解器,有利于计算的收敛。

4 计算结果和讨论

4.1 稳定温度场的形成

给热源(加热器)H 通电,产生焦耳热,把热量传递给周围气体,随着热量的变化,敏感结构内的温度场也将发生变化。图7 给出了热线TX2上温度随时间变化的曲线,图8～9 分别给出了0.2 s 和1.8 s 时的热源周围温度场云图和等温线图。从上述图可以看出,随着时间的推移,热线的温度逐渐增加,在1.8 s 时不再增加并保持稳定,此时热线和热源之间达到了一定的热平衡,热线处在一个稳定温度场当中,1.8 s 可以作为热气体加速度的开机预热时间。

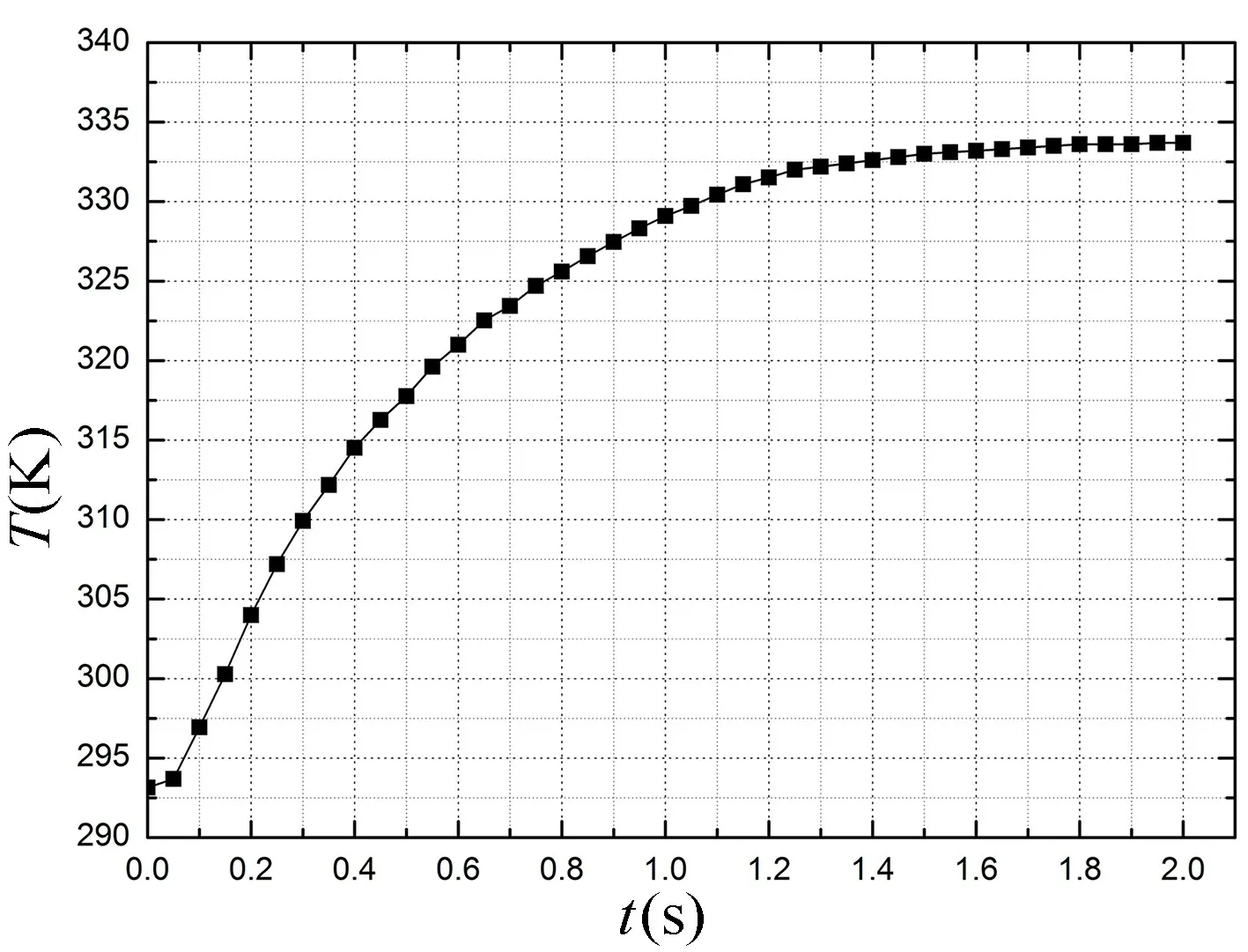
图7 热线TX2温度变化曲线Fig.7 Temperature change curve of hot line TX2

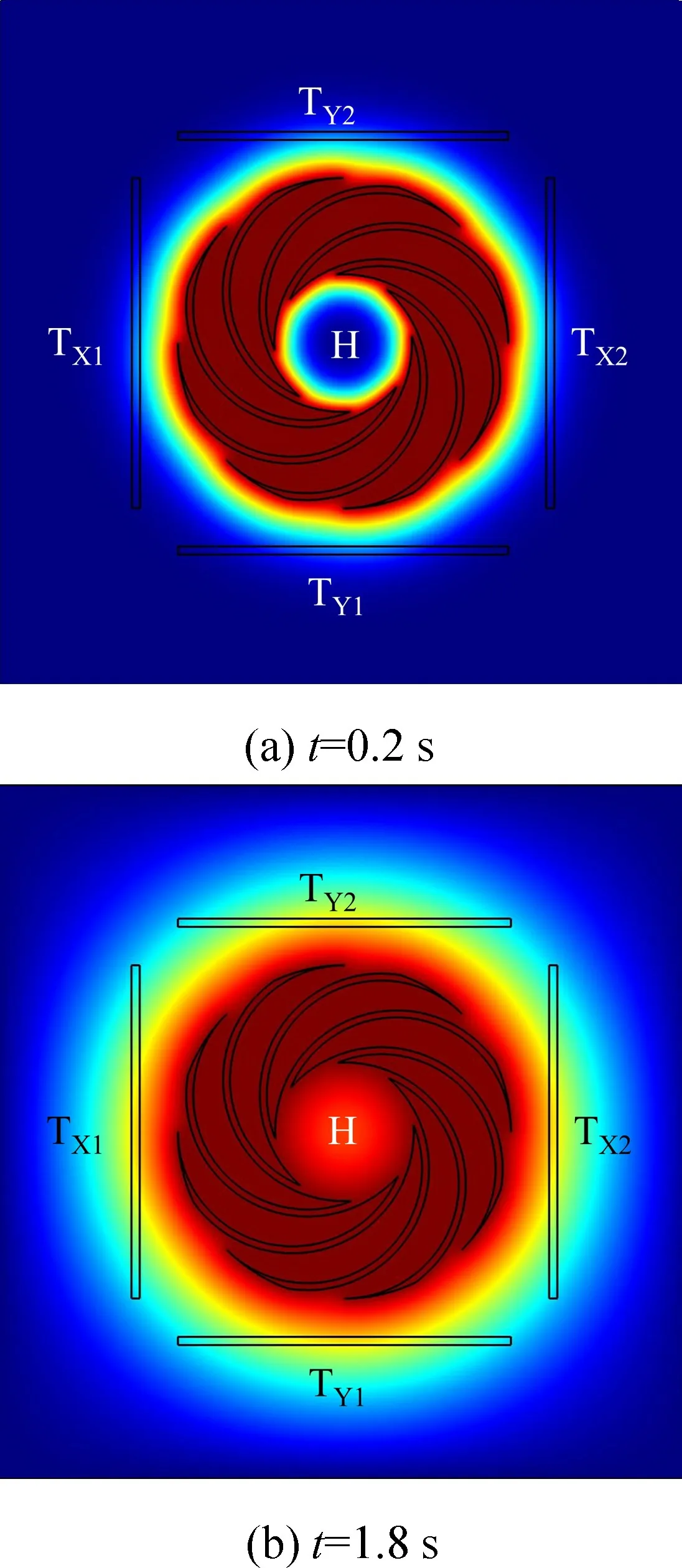
图8 敏感腔体内温度场云图的变化Fig.8 Changes of temperature field cloud atlas in sensitive cavity

4.2 加载加速度对温度场的影响

由图8(b)和图9(b)可以看出,在无加速度加载时,由于加热器(热源)加电产生焦耳热,在周围气体当中形成了一个稳定的温度场,沿着X方向的热线TX1和TX2和沿着Y方向的热线TY1和TY2温度场对称分布,热线TX1和TX2、TY1和TY2分别处在同一等温线,热线TX1和TX2、TY1和TY2温度相同,两对热线的温差ΔTX=0,ΔTY=0。图10～11 分别给出了有输入加速度作用下的温度场云图和等温线图。当输入加速度为ax=5g,ay=0g 时,加速度沿着X轴的正方向输入,在惯性力的作用下,热源沿着加速度方向X轴正方方向偏移;当输入加速度为ax=0g,ay=5g 时,加速度沿着Y轴的正方向输入,在惯性力的作用下,热源沿着加速度方向Y轴偏移。从图中可以看出,温度场的偏移造成了温度场相对于两对对称设置的热线TX1和TX2、TY1和TY2不再对称分布,靠近热源的热线TX2或TY2温度高于另一个热线TX1或TY1的温度,ΔTX＞0 或ΔTY＞0。当加速度沿着X和Y轴的负方向输入时,ΔTX＜0 或ΔTY＜0。因此根据温差的正负判断输入加速度的方向。

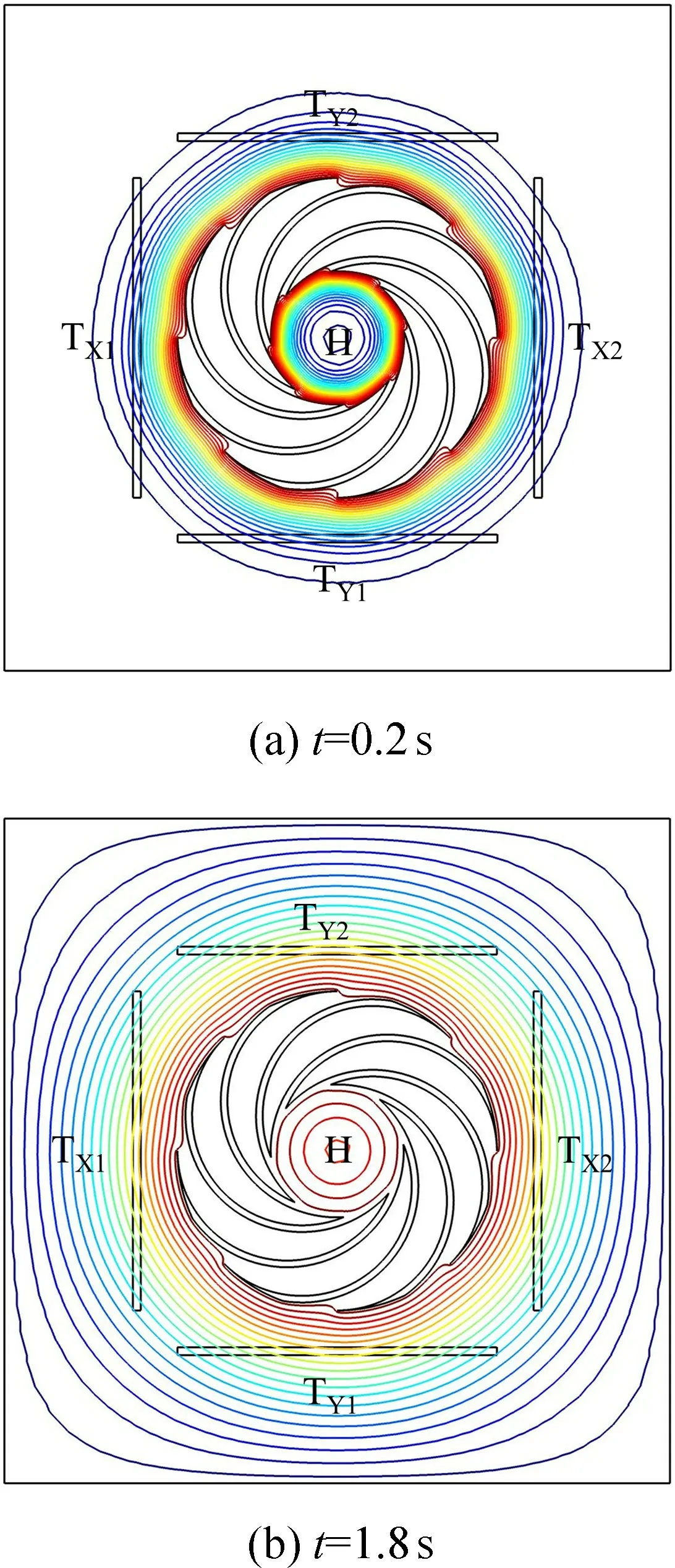
图9 敏感腔体内等温线图的变化Fig.9 Changes of isotherm in sensitive cavity

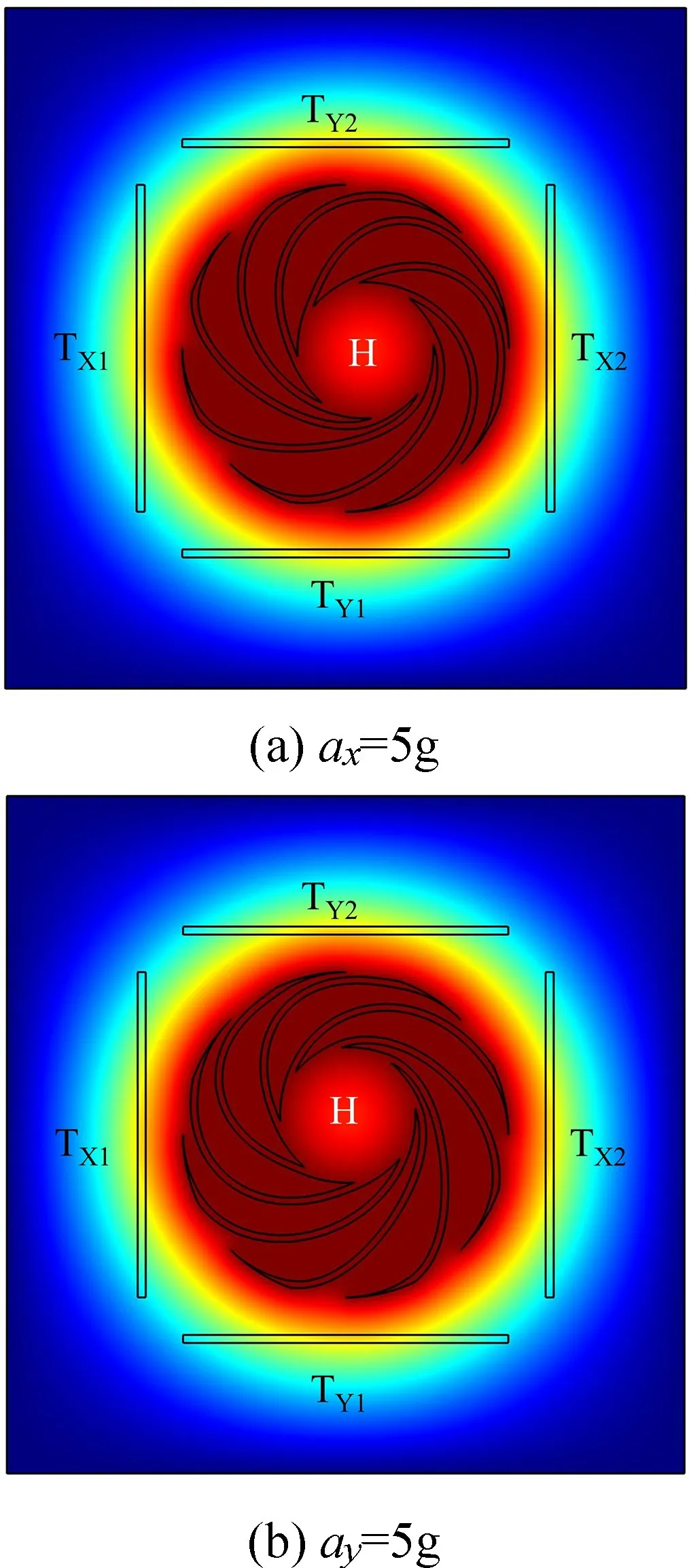
图10 X、Y 敏感轴加速度作用下的温度场云图分布Fig.10 Cloud atlas distribution of temperature field under acceleration of X and Y sensitive axes

下面来考察温差ΔTX和ΔTY是否随着输入加速度发生线性变化。图12 给出了两个热线TY1和TY2上的温差在输入Y正方向加载不同加速度时随时间的变化曲线。从该曲线可以看出,在加速度ay=2.5g 和ay=5g时两个热线的温差ΔTY随着时间发生变化,在1.8 s 附近温差趋于稳定,和上述结论吻合。在1.8 s 时加速度ay=2.5g 和ay=5g 时温差ΔTY分别为171 mK 和338 mK,基本是呈线性增长。同理可以得到在1.8 s 时加速度ax=2.5g 和ax=5g 时温差ΔTX分别为171 mK 和340 mK,也是呈线性增长。图13 给出了加载加速度为-5g～5g 范围内,两个热线TY1和TY2温差的变化曲线,经过计算该曲线的线性拟合直线成线性增长,斜率AY为73 mK/g,该斜率称之为Y敏感轴温度输出灵敏度,它给出了输入加速度ay和输出量ΔTY之间的关系。类似可以得到X敏感轴温度输出灵敏度AX为71 mK/g,它给出了输入加速度ax和输出量ΔTX之间的关系。两轴的平均温度灵敏度为72 mK/g。

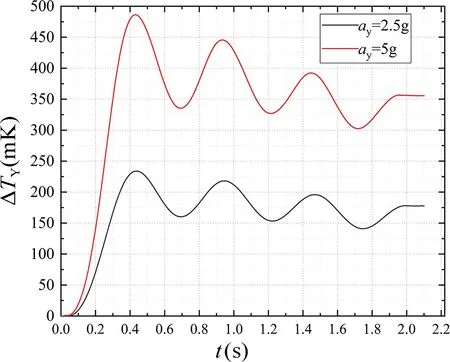
图12 输入不同加速度时Y 敏感方向两热线的温差Fig.12 Temperature difference between two hot wires in Y-sensitive direction under different accelerations

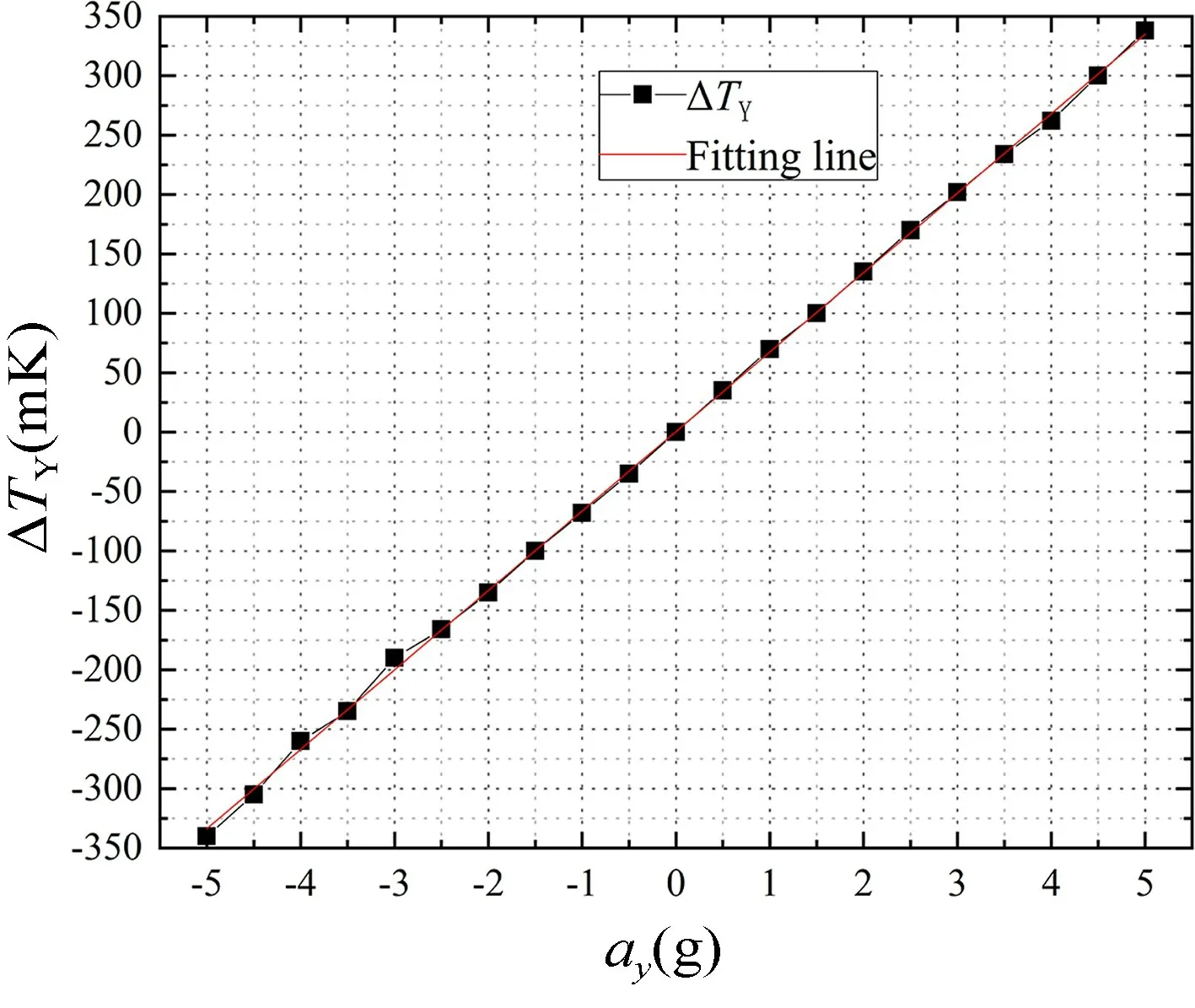
图13 热气体双轴加速度计的温度灵敏度曲线Fig.13 Temperature sensitivity curve of biaxial thermal gas accelerometer

4.3 热气体双轴加速度计的数学模型

以敏感轴Y轴为例给出该加速度计输入量ay和输出电量VYOUT之间的定量关系。根据上述分析,只要给出两个热线温差ΔTY和电桥的不平衡电压VYOUT之间的定量关系,就可以推导出该加速度计的输入量ay和输出电量VYOUT之间的定量关系,也就是该加速度计的数学模型。通过上述有限元计算可以得到温差ΔTY和输入加速度ay之间的定量关系:

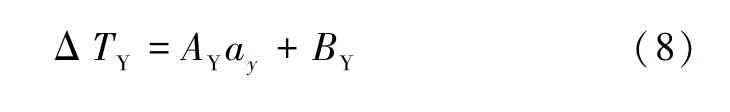
式中:AY是拟合直线ΔTY-ay的斜率;BY是拟合直线ΔTY-ay的截距。

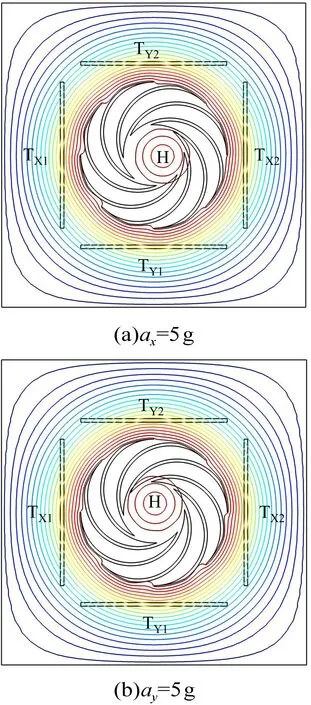
图11 X、Y 敏感轴加速度作用下的等温线分布Fig.11 Isotherm distribution of temperature field under acceleration of X and Y sensitive axes

把式(8)带入到式(2)中可以得到输入加速度ay和输出电压VYOUT之间的关系式:

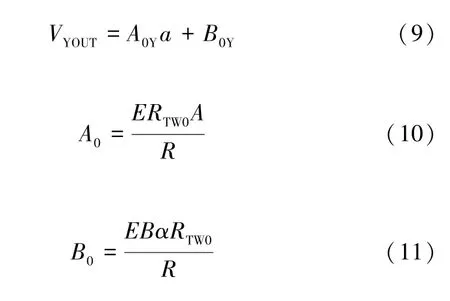
在式(10)和(11)中,A0Y和B0Y可以通过有限元计算拟合直线ΔTY-ay的斜率和截距获得,其他参数可以通过结构参数和材料参数获得,因此式(9)就是本论文提出的热加速度计Y轴输出数学模型,它给出了该加速度计输入量ay和输出电压VYOUT之间的定量关系,其中A0Y和B0Y分别为加速度计的Y轴输出灵敏度和Y轴输出零位电压。如图14 所示,给出了根据式(9)计算出来的该加速度计Y轴的输入-输出特性曲线。从特性曲线可以看出,在30 mW 的功率下,该加速度计Y轴的灵敏度为504 mV/g,非线性度为2.83%。X敏感轴的输入-输出数学模型与式(9)相似,类似地,可以得到敏感X轴的灵敏度为500 mV/g,非线性度为2.81%。两轴的平均灵敏度为502 mV/g,平均非线性度为2.82%。

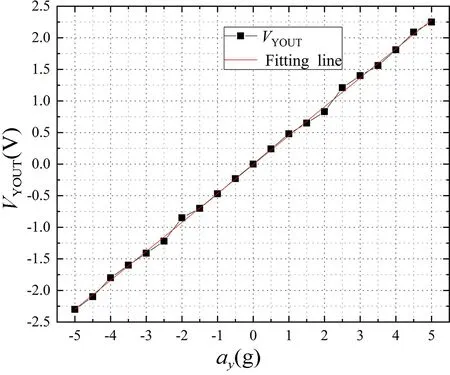
图14 热气体双轴加速度计的输入-输出特性曲线Fig.14 Input-output characteristic curve of biaxial thermal gas accelerometer

4.4 两敏感轴的交叉耦合

多轴一体传感器的关键指标之一是交叉耦合。设当加速度沿着X敏感轴满量程输入时,输出端的温差为ΔTXF.S和ΔTYF.S以及当加速度沿着Y敏感轴满量程输入时输出端的温差为ΔTYF.S和ΔTXF.S。分别定义两个敏感轴X、Y的交叉耦合分别为:

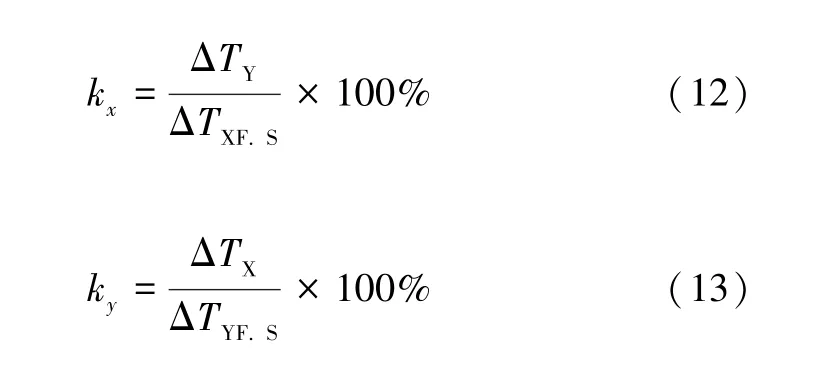
图15 给出了当敏感轴X轴满量程输入ax=5g 时,X轴输出和Y轴输出的比较。图16 给出了当敏感轴Y轴满量程输入ay=5g 时,Y轴输出和X轴输出的比较。从图中可以看出,该双轴加速度计的交叉耦合较小,敏感轴X的交叉耦合kx=2.2%,敏感轴Y的交叉耦合ky=2.4%,平均交叉耦合为2.3%。理想的交叉耦合将取决于工艺上能否保证敏感结构的正交性和垂直度。

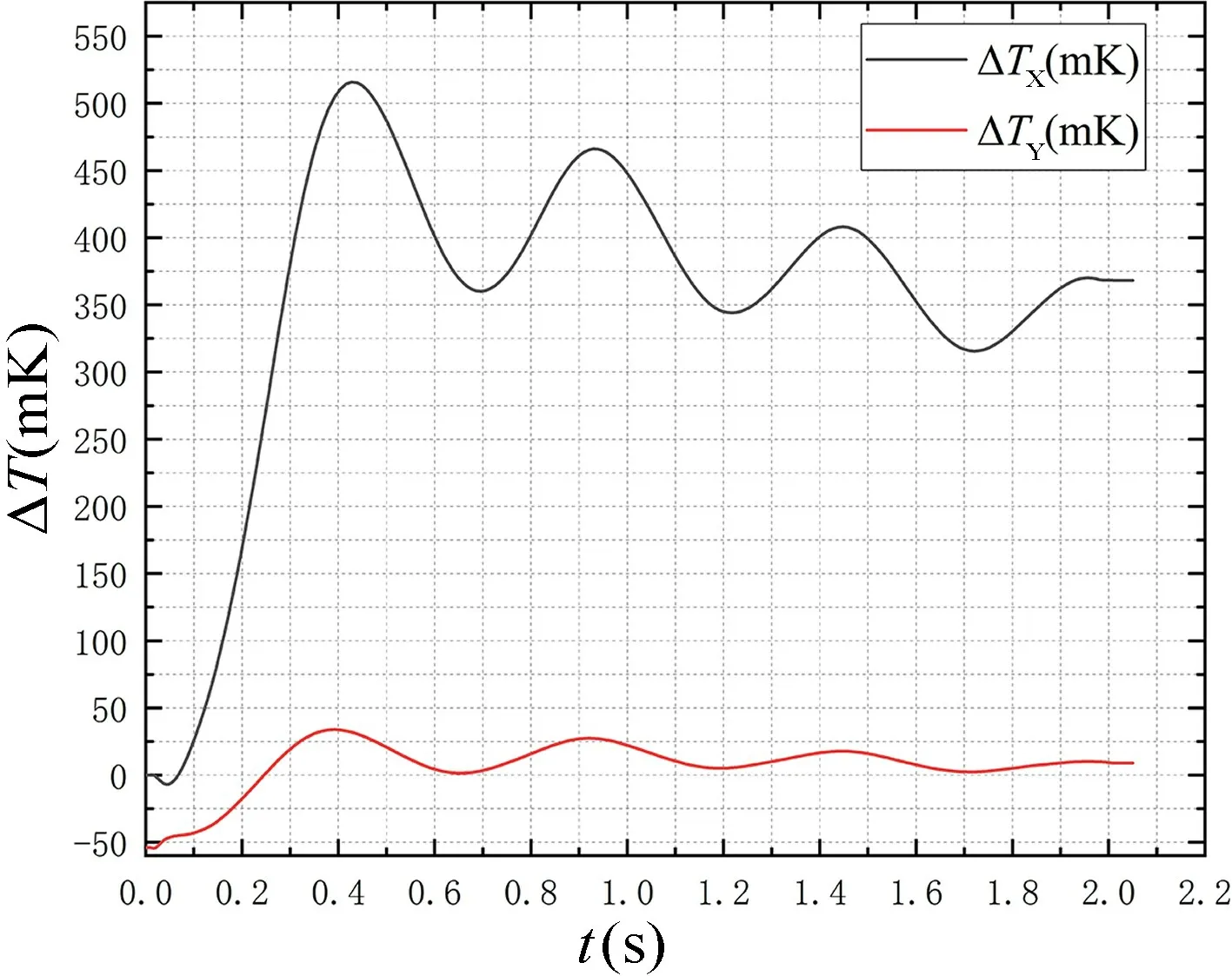
图15 输入加速度ax=5g 时, X 轴输出和Y 轴输出Fig.15 X-axis and Y-axis output when input acceleration ax=5g

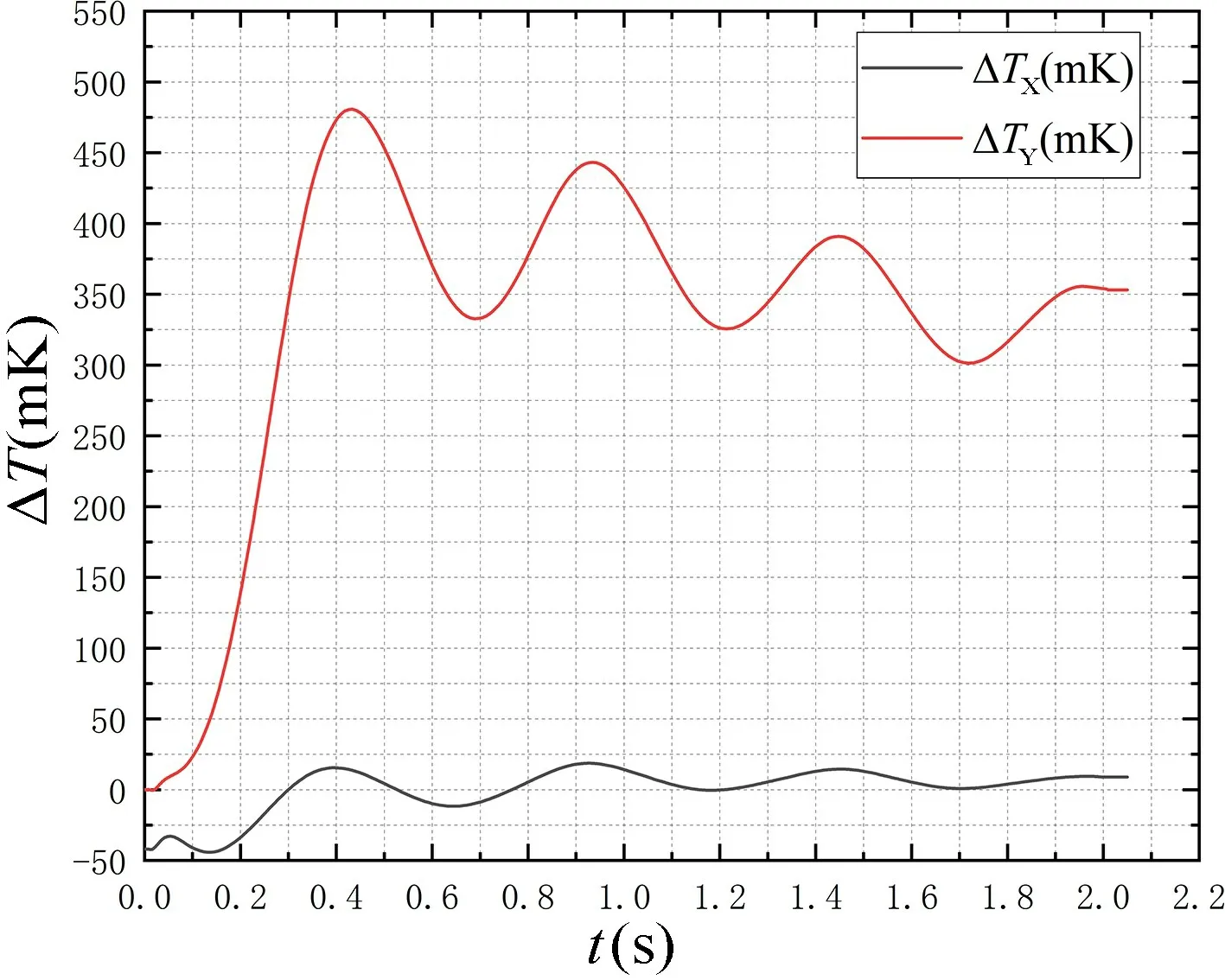
图16 输入加速度ay=5g 时, Y 轴输出和X 轴输出Fig.16 Y-axis and X-axis output when input acceleration ay=5g

5 结论

本文提出了一种新型动热源摆式双轴MEMS 热加速度计,对该双轴加速度计的敏感机理进行了研究。在给出双轴热加速度计结构原理的基础上,建立了二维双轴加速度计物理研究模型,通过划分网格、加载加速度等方法对双轴加速度计敏感元件内的温度场进行了计算。计算结果表明:

(1)当给动热源通电,产生焦耳热,热量传递给周围气体,在敏感元件内形成一个稳定的以动热源为中心的温度场,温度场形成时间小于1.8 s;

(2)当有加速度加载时,动热源沿着加速度的方向移动,温度场也向着加速度方向偏移,由此可以判断加载加速度的方向;

(3)当有加速度加载时,对称分布在动热源两侧等距离的两个热线处在不同的温度线上,动热源靠近的热线温度较高,两个正交敏感方向X、Y轴上的热线温差ΔTX、ΔTY不为零。温差ΔTX、ΔTY分别随着输入加速度ax和ay的加大呈现线性增长,X、Y两轴平均温度灵敏度分别为7.2×10-2K/g;

(4)将两对热线分别和平衡电阻组成信号提取电桥,可以将温差ΔTX、ΔTY转化为电压VXOUT和VYOUT输出,该电压输出与输入加速度ax和ay成正比,由此可以确定输入加速度的大小,实现了双轴输入加速度和输出电压的转换;

(5)根据线性拟合直线,得到该双轴加速度计的输入-输出特性ax-VXOUT和ay-VYOUT曲线,给出了加速度计的数学模型,揭示了该热加速度计的敏感机理,计算出该加速度计X、Y轴平均灵敏度为0.502 V/g,平均非线性度为2.82%,平均交叉耦合为2.3%。

本文提出的对称半圆形辐条的数量对传感器的灵敏度和量程都会有一定的影响,下一步需要对此做进一步的详细定量研究。本文为进一步优化该类双轴加速度计的结构、提高加速度计的性能奠定了理论基础。本文提出的加速度计灵敏度高、双轴测量误差小、结构简单、成本低,在消费电子、航空、航天、航海、汽车、生物医学和环境监控等微型运动载体姿态控制领域有广阔的应用前景[14]。