一种基于三维集成电路的多位碳纳米管硅通孔
关文博,吕红亮,张玉明,张义门
(西安电子科技大学 微电子学院,陕西 西安 710071)
硅通孔(Through Silicon Via,TSV)技术促进了三维集成电路的发展,它可以降低传统平面集成电路的局限性,缩短互连长度,提高集成密度,降低功耗[1]。然而,TSV 占据的面积远远大于片上通道。此外,任何衬底内的TSV 的数量都受到TSV 填充材料和衬底热膨胀系数之间的差异的限制。为了防止由于热应力导致的基片开裂,TSV 在硅衬底中所占的面积被限制在基片面积的2%左右[2-3]。因此,如何解决三维结构中各层之间的I/O 限制是一个主要问题。
碳纳米管(Carbon Nanotube,CNT)作为一种新兴材料,因其具有优越的电、热、机械性能,通常可取代铜(Cu)和钨(W)作为TSV 的填充材料。Cu 的电阻大约比每微米的CNT 束在传导方向上的电阻高2.5 倍,相反,束内相邻CNT 之间的电阻约为兆欧级别[4]。杭州电子科技大学的傅楷研究了填充碳纳米管的TSV 的传输特性,利用有效电导率对TSV 阻抗进行了提取,同时研究了CNT 填充比、温度和其他几何参数对传输性能的影响[5]。印度信息技术研究所的Rao 建立了Cu 和CNT混合填充TSV 的电学模型,所提出的模型包括不同比例的单壁碳纳米管(Single-Walled CNT,SWCNT)和多壁碳纳米管(Multi-Walled CNT,MWCNT)[6]。加州大学洛杉矶分校的Vaisband 提出了CNT TSV 与石墨烯互连界面的电学模型和热模型,利用COMSOL 软件对所提模型进行了仿真和验证,比较了CNT 与多层石墨烯(Multilayer Graphene,MLG)、CNT 与Cu 二者结构的电阻和热阻,表明用MLG 替代Cu 作为与CNT 的互连可大幅降低互连界面的电阻和热阻[7]。
除了不同填充材料和不同互连界面,对CNT 的传输信号数量也是I/O 限制的关键问题。Vaisband 首次提出了双位CNT TSV 的概念及其等效电路模型,对位之间的电容耦合和泄漏电流进行了评估[8]。随着工作频率的增加,差分信号因具有抑制共模噪声的能力和抗干扰的特性,通常被用来保证信号传输的完整性。作为最流行的差分传输信道形式之一,地面-信号-地面(Ground Signal-Signal-Ground,GSSG)型TSV 已经被建模、制造和分析,研究表明,GSSG 型TSV 是一种有效的降噪方法[9-10]。然而,在高密度TSV 阵列中,GSSG 型TSV 不可避免地受到相邻差分通道引起的差分模式噪声耦合的影响。杭州电子科技大学的赵文生团队基于双位CNT TSV 提出了新的差分型TSV(Differential TSV,D-TSV),研究了它的等效电路模型并采用部分元件等效电路(Partial Element Equivalent Circuit,PEEC)方法提取了相关阻抗,与传统的GSSG型TSV 相比,该模型具有更好的抗干扰特性[11]。
为了使3D 集成的层间I/O 进一步增强,需要TSV 具有更低的延迟时间和更小的面积。本文利用CNT 的各向异性提出了能够传输多个独立信号的三位CNT TSV,使得单个TSV 能够传递多个独立信号,这种功能是通过连接碳纳米管组以分离TSV 顶部和底部的pad 来实现的,pad 的材料为多层石墨烯。所提出的三位CNT TSV 可使层之间的I/O 数目加倍,并且不占用额外的衬底区域。换言之,可以用更少的三位TSV满足特定的层间I/O 数目要求,其俯视图如图1 所示。基于上述三位CNT TSV 的概念,作者在先前的研究中提出了一种新的差分多位CNT TSV[12]。本文在此基础上,进一步研究了三位CNT TSV 的电学特性,给出了三位CNT TSV 电阻和位间电容的计算方法。对差分型多位CNT TSV 在差模和共模条件下进行了变参数仿真,研究了多位CNT TSV 的时延特性。结果表明,所提出的多位CNT TSV 结构不仅可节省芯片面积,且具有优越的抗干扰能力和更好的时延性能。
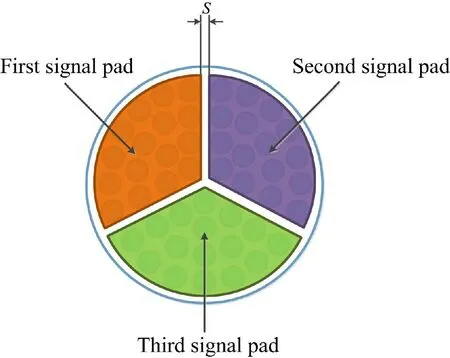
图1 三位CNT TSV 俯视图Fig.1 Top view of three-bit CNT TSV
1 三位CNT TSV 的电学特性
碳纳米管依据层数的不同可分为单壁碳纳米管和多壁碳纳米管。本文中,填充TSV 的MWCNT 的直径为20 nm,MWCNT 的最内层直径是其最外层直径的一半[13]。图2 为碳纳米管硅通孔示意图,Dout为CNT外壁直径;Din为CNT 内壁直径;m为相邻CNT 的距离(即范德瓦尔斯间距),其值为0.34 nm;Fm为金属性CNT 的比例,对于多壁碳纳米管其值为1/3[13];λ为电子有效平均自由程;rTSV为TSV 半径;H为TSV 高度;tox为氧化层SiO2厚度;s为TSV 内相邻两位之间分离的宽度;ε为碳纳米管的相对介电常数;ħ为约化普朗克常量;q为单位电子所带电荷量;m′表示相邻壳层之间的距离,设为0.34 nm。三位CNT TSV 数值计算中使用的电参数和物理参数列于表1[11,13,15]。

表1 三位CNT TSV 的电参数和物理参数Tab.1 Electrical and physical parameters of three-bit CNT TSV
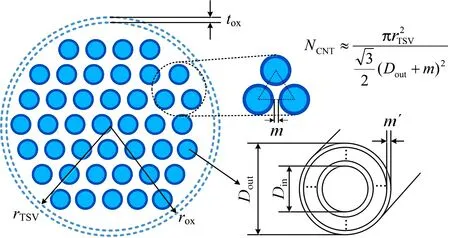
图2 三位CNT TSV 的横截面图Fig.2 Cross section of three-bit CNT TSV
多位TSV 的电学特性是由CNT(作为TSV 填充材料的CNT 阵列)的性质决定的。在1.1 节中给出了三位CNT TSV 的垂直和水平等效电导率。在1.2 节中给出了各位之间的耦合电容。
1.1 三位TSV 的电导率
MWCNT 的壳层数量可以表示为:
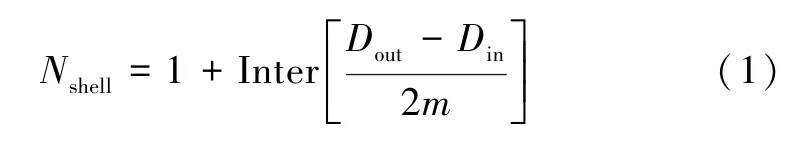
式中: “ Inter[·] ” 表示取整数。对于SWCNT,其值为1。第i个壳层的直径为:
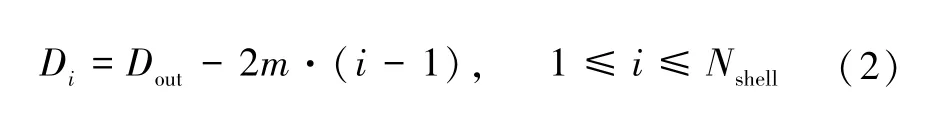
由文献[14]可知,CNT 束沿竖直方向的电阻为:
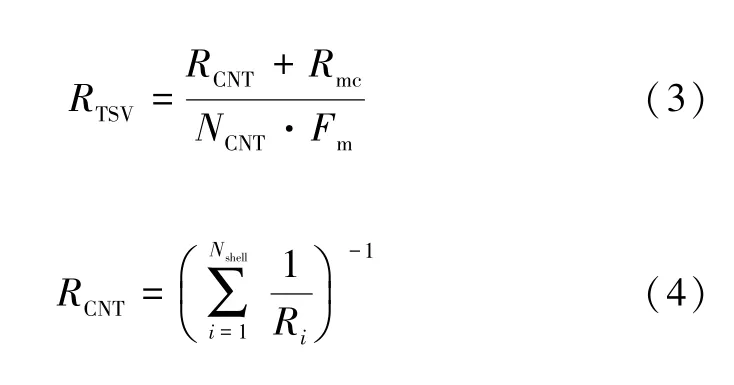
式中:RCNT是单根CNT 的电阻;Rmc为接触电阻;NCNT是一束CNT 的数量,在图2 中表示了它的大小。如图2 所示,MWCNT 中的每个壳层可以视为SWCNT,并且MWCNT可以看作由多个SWCNT 以同轴方式组成。因此,RCNT可以用公式(4)表示,其中Ri表示第i个壳层的电阻。
第i个壳层的电阻可以表示为Ri=RQi+RSi,其中RQi为量子电阻,它的值为RQi=h/(2q2Ni) (h是普朗克常数,Ni是第i个壳层的导电通道数);RSi为散射电阻,它的值为RSi=h·H/(2q2λNi) ;λ的计算过程可参考文献[15],此处取值为1 μm。
假设MWCNT 中1/3 的壳层是金属性的,而其他壳层是半导体性的,则第i个壳层的导电通道数可表示为[13]:

式中:DT=1300 nm·K。
在本文中,三位CNT TSV 结构顶部pad 的材料为MLG。接触电阻Rmc的大小基于CNT 和MLG 之间共价键的质量[7]。因此,Rmc可表示为[7]:

式中:ρQ是由CNT 和MLG 之间的共价键所确定的界面处电阻率,其值为0.24 Ω·μm2;Aint是界面处的横截面积[7]。
因此,CNT 束沿竖直方向的电阻可表示为:
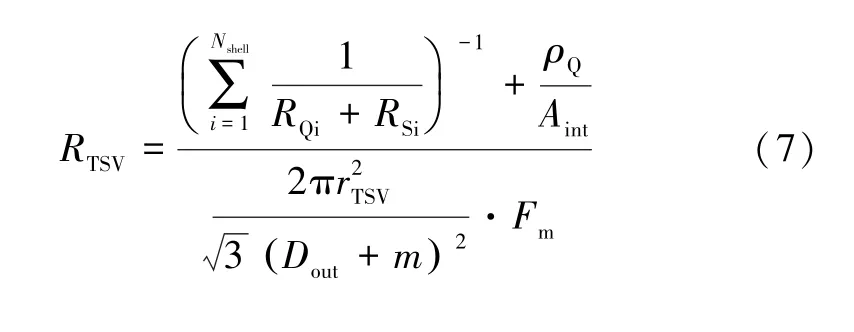
三位CNT TSV 沿垂直方向和水平方向的等效电导率与文献[8]中类似,分别可表示为:

单个TSV 被碳纳米管划分以传递多个独立信号,由于传导该信号的CNT 减少,因此每部分的TSV 电阻将增大。TSV 各位的电阻为:
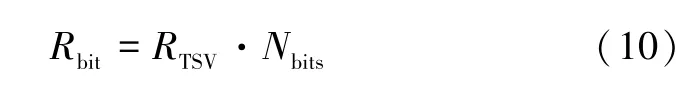
式中:Nbits表示多位TSV 中传播的独立信号的数目,此处取值为3。多位TSV 内任意两位之间的电阻可表示为:

1.2 三位TSV 的电容
CNT 的各向异性使得多位TSV 任意两位之间具有绝缘性质。与文献[8]中类似,三位TSV 任意两位之间的电容可以用平行板电容的表达式来近似,相邻两位之间间隔的宽度s可类比于平行板之间的距离d,平行板的面积是TSV 沿CNT 的纵向截面积。如图3所示,与文献[8]中双位TSV 相比,该面积约为双位TSV 纵向截面积的1/2。因此三位TSV 两位之间的电容为:
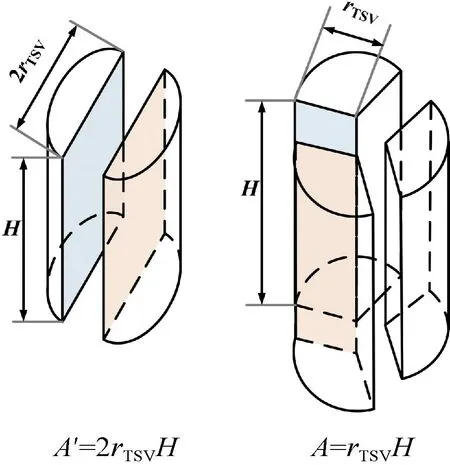
图3 两位TSV 和三位TSV 电容模型的面积比较Fig.3 Area comparison of capacitance models of two-bit TSV and three-bit TSV
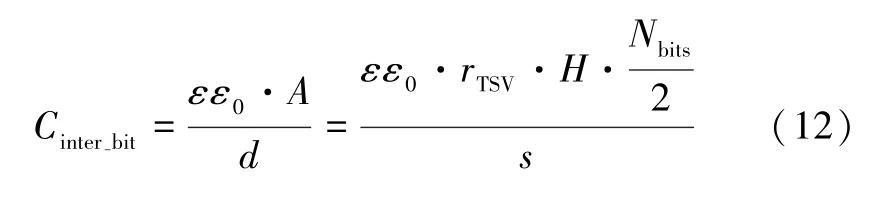
式中:ε和ε0分别表示碳纳米管的相对介电常数和真空介电常数[8]。此时,Nbits/2=3/2。
1.3 三位TSV 的电流密度分布
CNT TSV 的电流密度在径向上可表示为[16]:
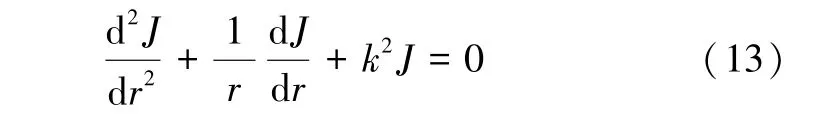
式中:k=,μ=4π×10-7H/m 为真空磁导率。通过求解式(13)可将CNT TSV 的电流密度归一化表示为:
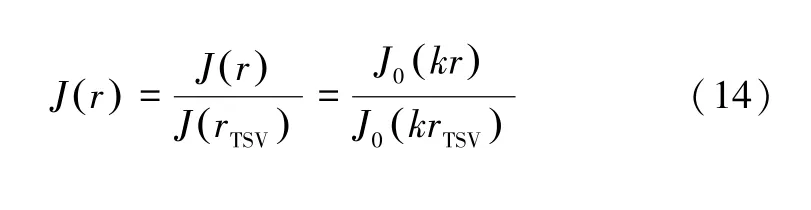
式中:J0(·) 为第一类零阶贝塞尔函数。CNT TSV 的趋肤深度可表示为:

图4 给出了不同频率和温度下SWCNT 和MWCNT 中的归一化电流密度分布曲线,其中SWCNT的Fm取决于加工工艺,本文假设为0.9(目前最高可达0.91[17]),其余参数列于表1。从图4 中可以看出随着频率的升高,SWCNT TSV 和MWCNT TSV 的趋肤深度随之增大,但在相同条件下MWCNT TSV 的趋肤深度远小于传统铜TSV 的趋肤深度[18]。此外,随着温度的升高,SWCNT TSV 中的趋肤效应被略微抑制,但MWCNT TSV 几乎没有变化。

图4 不同频率和温度下的归一化电流密度分布。(a) SWCNT;(b)MWCNTFig.4 Normalized current density distribution at different frequencies and temperatures.(a) SWCNT;(b)MWCNT
1.4 三位TSV 的电学评估
在HFSS 中评估了三位TSV 的电学特性,其中填充TSV 所用的CNT 的电导率由式(8)和式(9)确定。三位TSV 的测试结构如图5 所示,该结构用于评估CNT TSV 各个位在垂直和水平方向上的电性能。
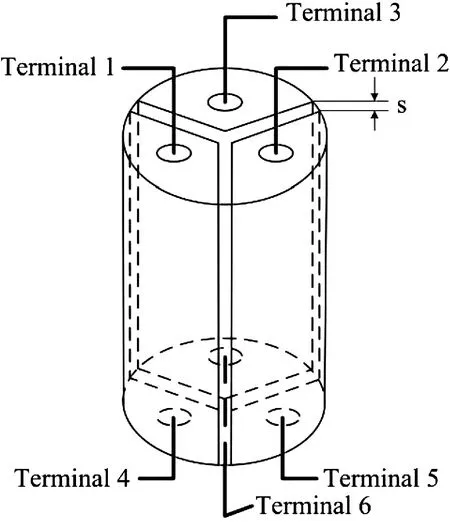
图5 三位CNT TSV 的仿真测试结构Fig.5 The test structure of three-bit CNT TSV
表2 列出了三位TSV 内每个终端之间的HFSS 数值计算电阻。由于三位TSV 是对称结构,所以每对终端之间的电阻是相同的。与文献[8]中双位CNT TSV的竖直电阻和水平电阻相比均明显增大,这是因为位数的增加使得传导该信号的CNT 束数量减少,水平电阻越大说明三位TSV 在位之间的水平方向上越不容易传播信号,即发生漏电的可能性很低。而在传播方向上的竖直电阻的增大与水平电阻的变化相比,可忽略不计。三位TSV 的竖直电阻和水平电阻之比约为1890,该比值与文献[8]中双位CNT TSV 的竖直电阻和水平电阻之比近似相等。在HFSS 中还评估了TSV各位之间的电容Cinter-bit值为10.62 fF。
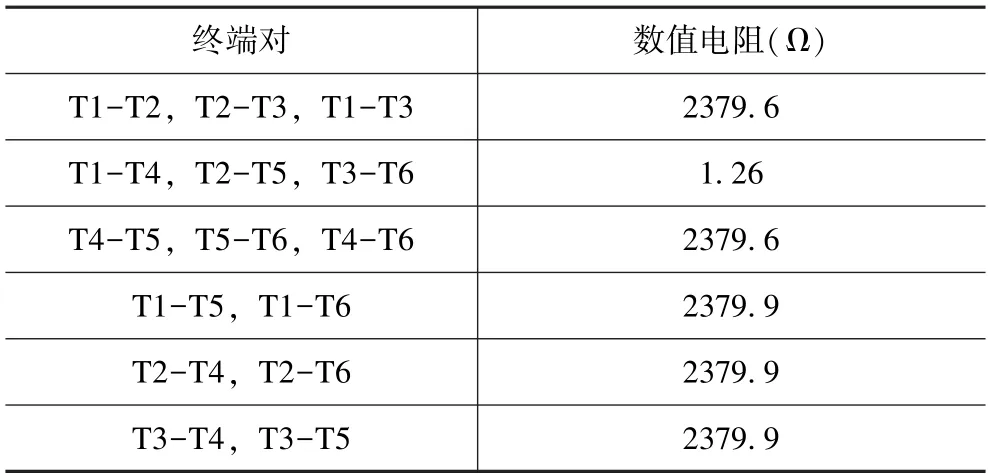
表2 三位CNT TSV 各位之间的电阻Tab.2 Resistance of each terminal pair of three-bit CNT TSV
图6 为三位CNT TSV 的等效电路模型。根据表1所列参数,无源元件的数值由式(10)、(11)和(12)确定,三位CNT TSV 各无源元件的数值为:Rbit=1.22 Ω,Rinter-bit=2372.46 Ω,Cinter-bit=10.63 fF。理论值和HFSS 对Rbit、Rinter-bit和Cinter-bit的评估值之间的误差分别为3%,0.3%和0.09%。
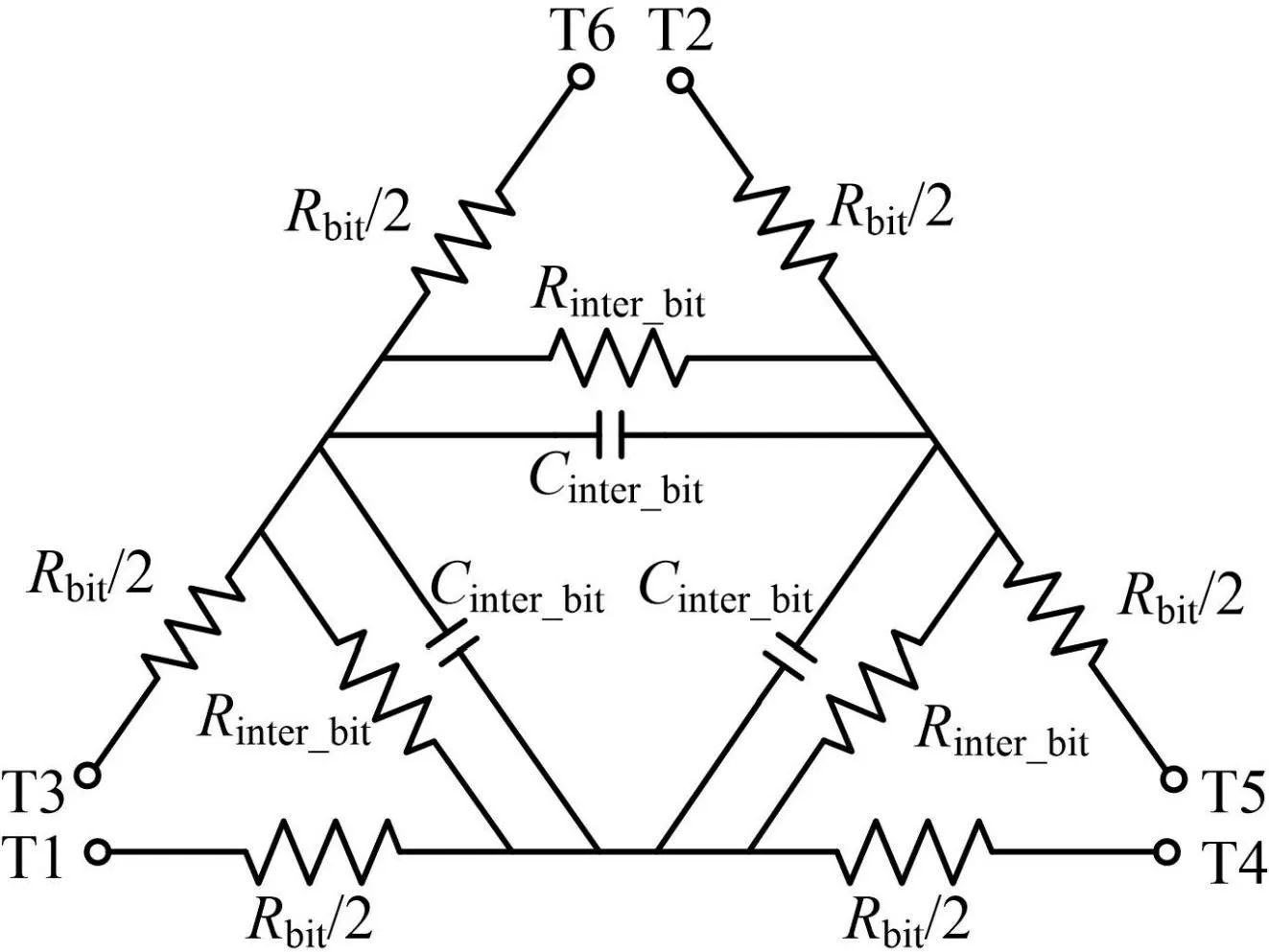
图6 三位CNT TSV 的等效电路模型Fig.6 Equivalent circuit model of three-bit CNT TSV
在ADS 中搭建如图6 等效电路,提取该模型的S参数,并与HFSS 中三位TSV 结构的S参数进行比较,仿真比对结果如图7 所示,由结果可知二者S参数曲线基本吻合,误差在1.2%以内。
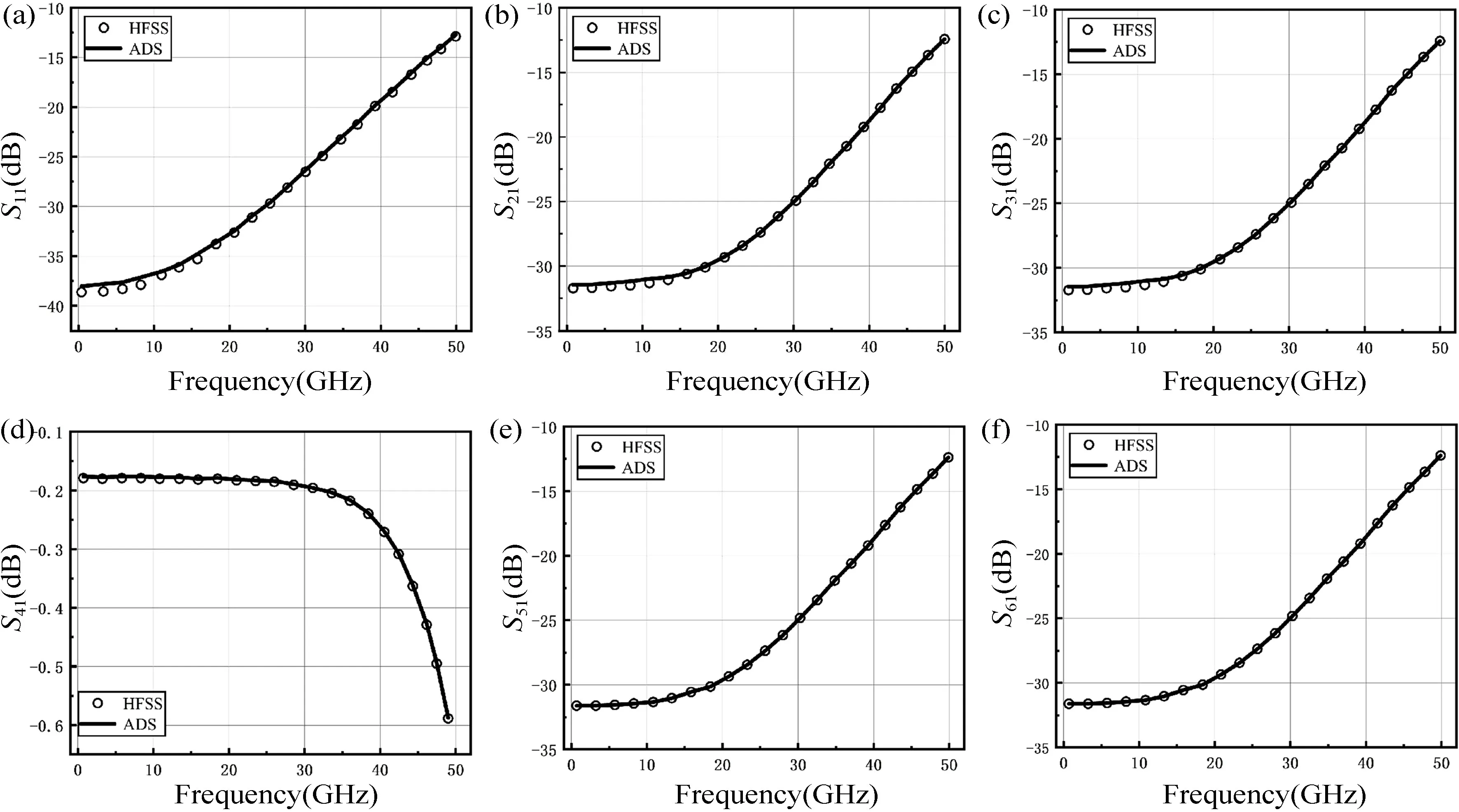
图7 HFSS 和ADS 中三位CNT TSV 的S 参数比较。(a) S11;(b) S21;(c) S31;(d) S41;(e) S51;(f) S61Fig.7 Comparison of S parameters of three-bit CNT TSV in HFSS and ADS.(a) S11;(b) S21;(c) S31;(d) S41;(e) S51;(f) S61
2 差分型多位CNT TSV
差分型多位CNT TSV 的原理图如图8 所示,其中所用三位CNT TSV 的相关几何参数如表1 所示,TSV之间间距L为30 μm。基于三位CNT TSV,所提出的差分型多位CNT TSV 只需要两个通孔,与传统的GSSG 型TSV 四个通孔相比节省了50%的芯片面积。两个三位TSV 的相邻两位作为信号通道,可传输两组极性相反的信号构成差分信号。

图8 差分型多位CNT TSV 的原理图Fig.8 The schematic diagram of the differential multi-bit CNT TSV
图9 为差分型多位CNT TSV 的等效电路图。Cox为TSV 的氧化层电容,它的值可以表示为Cox=2πεoxH/ln(rox/rTSV),其中εox是SiO2的介电常数。如图2所示,rox=rTSV+tox。在建模过程中,由于相邻TSV之间的距离比TSV 的半径大30 倍,相邻TSV 之间的耦合关系可以被认定为弱耦合关系,因此邻近效应的影响可以被忽略[14,19]。硅的电容和电导分别可表示为CSi=πεSiH/ln(L/rox) 和GSi=σSiCSi/εSi,其中εSi和σSi分别为硅衬底的介电常数和电导率。Cox、CSi和GSi的计算值分别为50.62 fF,8.25 fF 和0.002 S,Rbit、Rinter-bit和Cinter_bit沿用上一节三位CNT TSV 的理论值。
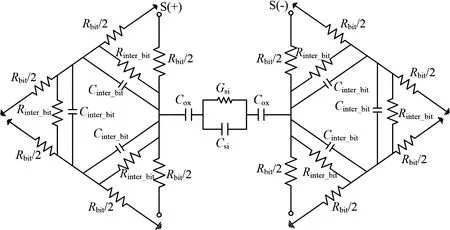
图9 差分型多位CNT TSV 等效电路图Fig.9 Equivalent circuit of differential multi-bit CNT TSV
为了验证所提出的差分型多位CNT TSV 的等效电路模型,分别在差模和共模条件下,对比了等效电路模型与HFSS 仿真的S参数,仿真结果如图10 所示。结果表明,所建立的电路模型在0~50 GHz 的整个频率范围内能够很好地预测TSV 的S参数。
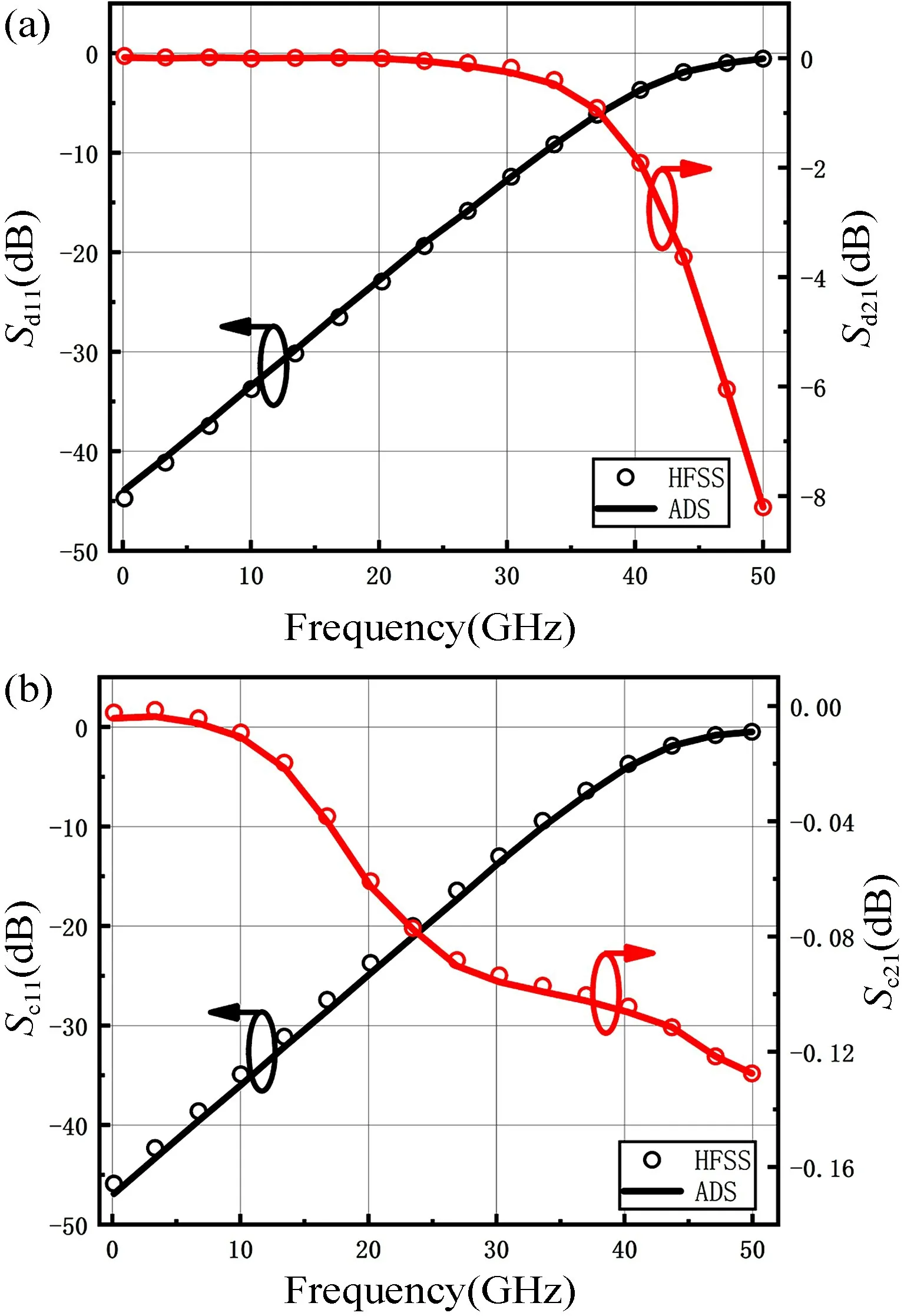
图10 等效电路模型和HFSS 仿真的S 参数对比。(a) Sd11, Sd21;(b) Sc11, Sc21Fig.10 Comparison of S parameters between equivalent circuit model and HFSS simulation.(a) Sd11, Sd21;(b) Sc11, Sc21
与传统的GSSG 型TSV 相比,所提出的差分型多位CNT TSV 在面积和抗干扰能力方面均优于传统的GSSG 型TSV。将CNT 作为TSV 的填充材料不仅有利于芯片散热,更重要的是,所提出的差分型多位CNT TSV 能够帮助抑制高密度TSV 阵列中相邻TSV 之间的串扰耦合。为了证明这一特性,使用HFSS 完成了如下仿真。如图11 所示,在每组模型中,一组充当干扰源,另一组充当受干扰对象。在差分模式下源端和负载端均接50 Ω 电阻,分别比较近远两端的耦合系数SD13和SD14。仿真结果如图12 所示,与传统的GSSG型TSV 相比,差分型多位CNT TSV 具有明显的抗干扰能力。
此外,为了将文献[11]和文献[19]中GS-SG 型TSV 和G-SS-G 型TSV 与所提出的三位差分型TSV进行抗干扰对比,将它们采用统一的物理和几何参数,相关参数值如表1 所示,L均为30 μm,以此排除由于参数不同而造成的结果差异。G-SS-G 型TSV 和GS-SG 型TSV 的顶视图如图11 所示,二者均利用CNT 束形成双位TSV 来传输差分信号。从图12 仿真结果中得出,所提出的差分型三位CNT TSV 与文献[19]中的TSV 相比具有更好的抗干扰能力。差分型三位CNT TSV 与文献[11]中GS-SG 型的TSV 抗干扰能力近似,但与其相比少用一根TSV,从而节约了衬底使用面积,同时增加了各层之间的I/O 数目。

图11 四种不同类型TSV 的俯视图。(a)传统GSSG 型TSV;(b)文献[19]G-SS-G 型TSV;(c)文献[11]GS-SG 型TSV;(d)提出的差分型三位CNT TSVFig.11 Top view of four different types of TSV.(a) Traditional GSSG TSV;(b) G-SS-G TSV in [19];(c) GS-SG TSV in [11];(d) The proposed differential three-bit CNT TSV

图12 相邻阵列TSV 之间串扰比较。(a)近端;(b)远端Fig.12 Crosstalk comparison between adjacent array TSVs.(a) Near-end;(b) Far-end
在差模和共模条件下,各结构参数对多位CNT TSV 的S参数的影响如图13 所示。rTSV对两种条件下的TSV 插入损耗的影响如图13(a)和(b)所示。随着频率的增加,差模和共模条件下的插入损耗都会降低。在相同频率下,随着TSV 半径的减小,TSV 电阻和导体损耗增加,这导致了更高的信号损耗。TSV 间距对插入损耗的影响如图13(c)和(d)所示。在低频下,TSV 间距对S21参数的影响可以忽略不计,但在高频下,差模和共模的S21参数随着间距的增加而增加。这是因为衬底电导在高频下起主要作用,而增加TSV 间距可能会降低漏电路径的电导和介电损耗[20]。介质层厚度和衬底电导率对插入损耗的影响分别如图13(e~h)所示。从图中可以看出,差模插入损耗几乎没有变化,而相比之下共模插入损耗随着tox和σSi的变化而显著变化。
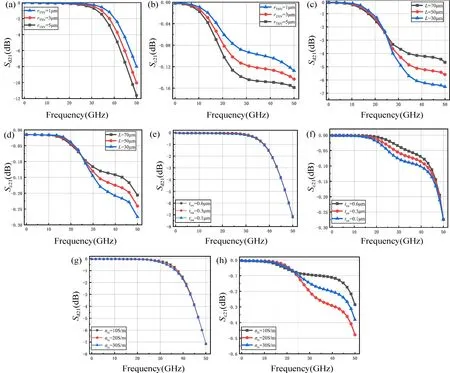
图13 不同结构参数下差分型多位CNT TSV 的差模和共模S 参数变化。(a) Sd21, rTSV;(b) Sc21, rTSV;(c)Sd21, L;(d) Sc21, L;(e) Sd21, tox;(f)Sc21, tox;(g) Sd21,σSi ;(h) Sc21,σSiFig.13 Differential mode and common mode S parameters of the differential multi-bit CNT TSV with different structural parameters.(a) Sd21, rTSV;(b) Sc21, rTSV;(c)Sd21, L;(d) Sc21, L;(e) Sd21, tox;(f)Sc21, tox;(g) Sd21,σSi ;(h) Sc21,σSi
最后讨论了所提出的三位CNT TSV 的制造工艺流程[21]。如图14 所示,首先在硅与二氧化硅的基板上沉积一个圆形金属板,将掩模版放置在金属板的两侧,通过选择合适的生长温度和压力,形成MWCNT。为了减小阻抗,将生长得到的MWCNT 进行致密化处理,将其转移到预先使用深反应离子刻蚀(Deep Reactive Ion Etching,DRIE)工艺刻蚀的通孔中。接着去除生长基底,经过氧化处理填充MWCNT 与通孔之间的间隙,之后对MWCNT 采用平坦化处理[22]。最后,在CNT TSV 的表面沉积三个独立的金属焊盘以促进差分信号传递。
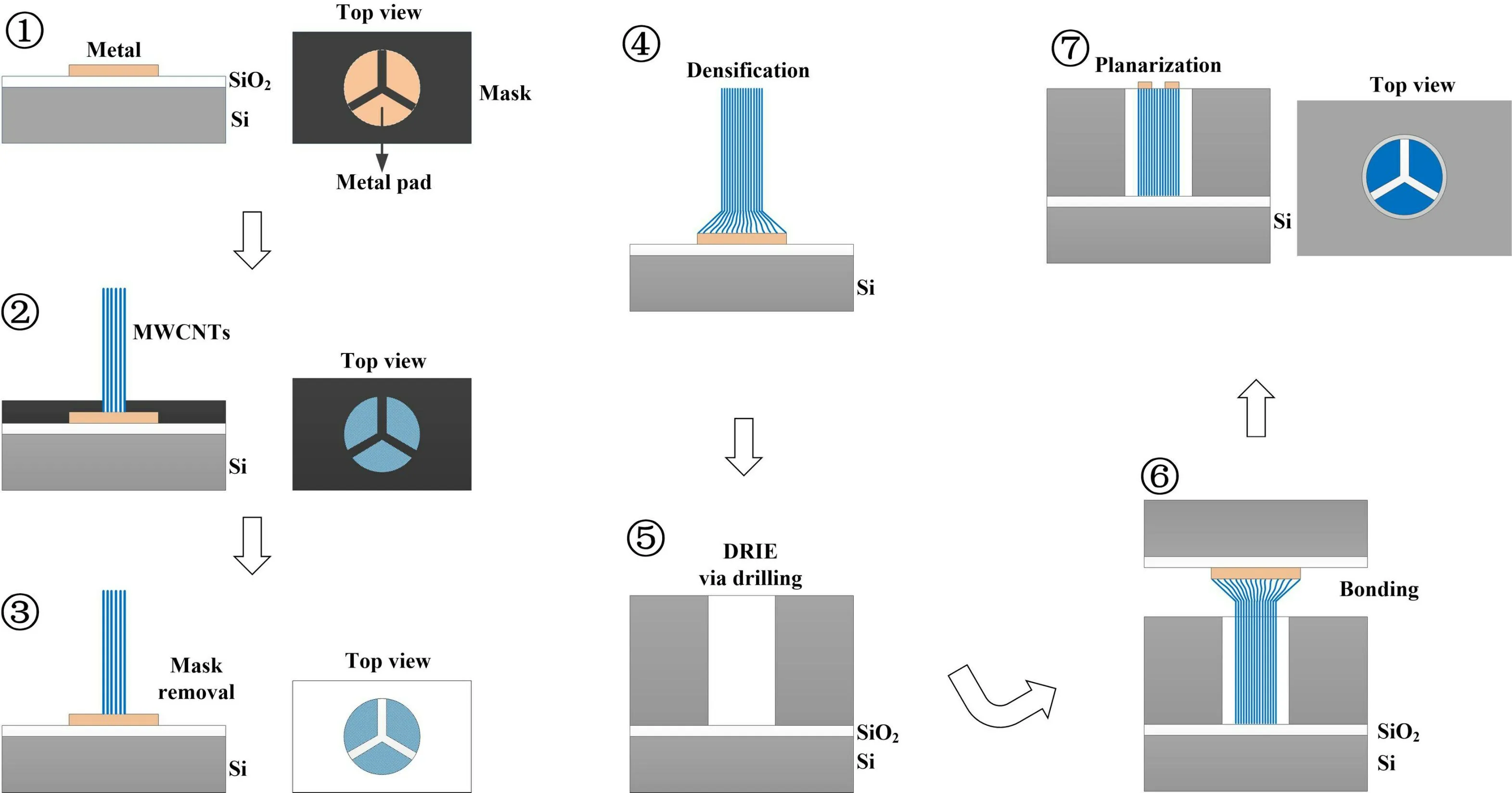
图14 所提三位CNT TSV 的工艺流程Fig.14 Process steps involved for the proposed three-bit CNT TSV
3 差分型多位CNT TSV 的时域特性
根据图9 等效电路模型,在ADS 中采用CMOS 反相器作为驱动,研究差分型多位CNT TSV 的时延特性[23-24]。在表1 所示参数下,分别在GSSG 型TSV 与所提出的差分型多位CNT TSV 的通孔信号端输入数据速率为50 Gbps、上升时间20 ps 且幅度1 V 的电压信号进行仿真,仿真结果如图15 所示,所提出的差分型多位CNT TSV 模型相比于传统的GSSG 型具有更好的时延性能。
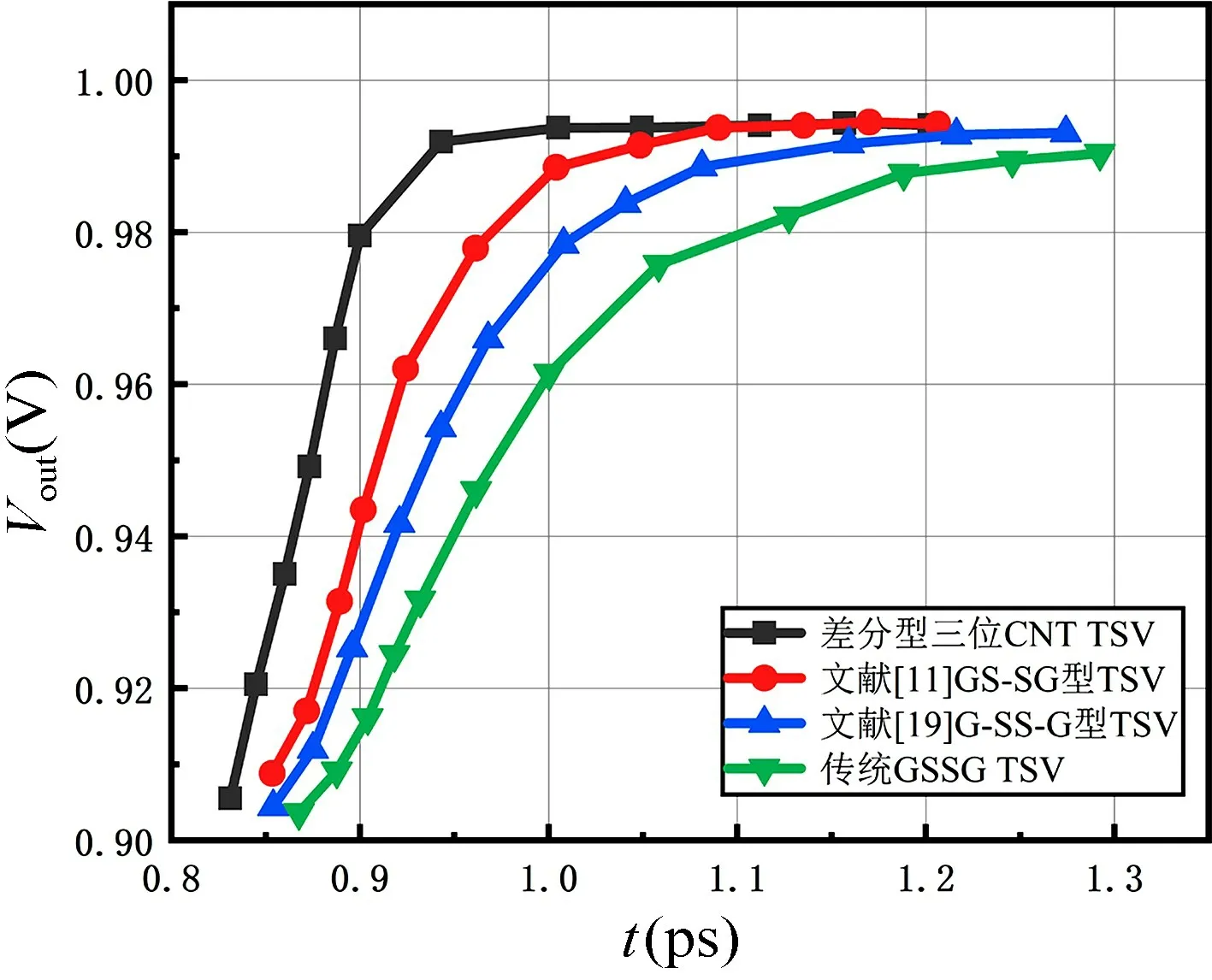
图15 不同TSV 模型下的时延对比Fig.15 The comparison of time delay under different TSV
此外,为了与双位差分型TSV 的时延性能进行比较,本文利用文献[11]和文献[19]中GS-SG 型TSV和G-SS-G 型TSV 的等效电路模型,将两种双位TSV通孔信号端分别输入以上电压信号进行仿真。对差分型多位CNT TSV 在4 GHz 频率、上升下降沿100 ps、500 mV 电压下进行眼图仿真,其结果如图16 所示。由图可知,所提出模型具有良好的信号完整性,峰值抖动几乎为零。
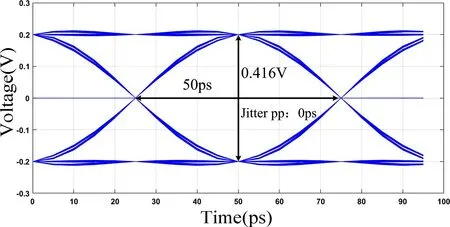
图16 差分型多位CNT TSV 的信号眼图Fig.16 Eye diagram of differential multi-bit CNT TSV
4 结论
本文提出了一种三位CNT TSV。每个TSV 可以携带多个独立的信号,大大增加了三维集成电路中的I/O 数量。利用HFSS 对三位CNT TSV 各寄生参数进行了数值计算,并仿真得出了它的S参数。此外,在ADS 中对三位CNT TSV 的等效电路模型进行了评价,与数值模型相比具有较高的精度,各寄生参数的误差大小在3%以内,S参数误差大小在1.2%以内。
基于三位CNT TSV 的概念,提出了新的差分型多位CNT TSV。所提出的差分型多位CNT TSV 只需要两个孔,从而节省了芯片面积,提高了集成密度。建立了差分型多位CNT TSV 的等效电路模型,通过与HFSS 仿真结果的比较,验证了该电路模型的精度可达50 GHz。并与传统GSSG 型TSV 以及两种新型双位TSV(G-SS-G 型和GS-SG 型)进行了对比,仿真结果表明所提出的差分型多位CNT TSV 具有优越的抗干扰能力和更好的时延性能。对差分型多位CNT TSV 在差模和共模条件下进行了变参数仿真。讨论了三位CNT TSV 的制造工艺流程。最后,对所提出TSV 结构进行时域眼图仿真,结果表明新结构具有良好的信号完整性。

