多层瓷介高压电容器空洞缺陷引起的畸变电场有限元分析

梁栋程,王淑杰,季航

(中国工程物理研究院 计量测试中心,四川 绵阳 621999)

电介质材料的应用已有多年的历史,但早期电介质仅作为分隔电流的绝缘材料来使用,随着人类对物质微观结构认识的逐步提高,尤其是自20 世纪30 年代以来,对物质内部电极化过程研究逐步深入,电介质材料的应用得到了很大的发展[1]。在军用领域,电介质材料的应用对元器件可靠性的提高和装备小型化的发展均发挥了积极作用,典型应用包括多层瓷介高功率脉冲电容器、LTCC 滤波器等。相关文献报道了电介质材料应用研究方面取得的进展,主要是通过元素掺杂、离子取代、组分设计等方式,采用相应的工艺控制,以提高储能密度、效率、温度稳定性、介电性能、击穿场强等宏观性能[2-7]。

然而,在军用领域,元器件内部空洞、分层、裂纹等缺陷引起的可靠性问题同样值得关注。这类工艺过程中产生的缺陷在初期并不一定会引起失效,但在使用过程中就会以一定的概率引起失效,对装备系统造成不良影响。因此,研究这类缺陷对可靠性的影响机制和趋势,并建立相应的评价依据,对于保障元器件的可靠性具有较强的现实意义。一些文献报道了裂纹、空洞、分层、电极结瘤、电极不连续等工艺缺陷会产生畸变电场、局部电流集中等现象,从而引发瓷介元件失效[8-10]。这类关于失效分析的文献对元器件质量保证工作具有一定的参考价值,但在践行“预防型” 的质量管理模式下,不仅需要知道工艺缺陷种类对可靠性的影响因素,还需要获取工艺缺陷大小对可靠性的影响趋势及机制。鉴于现有无损检测方法的局限性,本文拟借助有限元分析手段,从理论上分析相关影响趋势及机制,为后续建立相应的量化评价依据提供数据支撑,同时也为同类研究在方法上提供一定的参考。

在上述工艺缺陷类型中,空洞缺陷引起的失效值得关注,从瓷介电容、LTCC 滤波器的制备工艺来说,均要进行排粘、烧结等过程,主要目的是去除前面浆料配置工艺中留下的有机溶剂或各种高分子材料,避免产生空洞缺陷。这类工艺缺陷引起的电击穿失效是最为常见的失效模式之一。Chen 等[11]研究了空洞尺寸对电容内部局部放电的影响,结果表明局部放电量和放电起始电压取决于陶瓷内部最大空洞尺寸。Xu[12]对单个空洞附近的场强进行了有限元模拟计算,结果表明该处附近场强会增加50%。

上述文献均表明空洞会引起畸变电场,导致介质材料内部局部区域电场过大,从而引发击穿,但畸变电场产生的理论以及相关机制却鲜有报道。本文采用有限元仿真计算了空洞产生的畸变电场大小以及变化趋势,利用麦克斯韦边值关系理论解释了畸变电场产生的原因。分析了影响畸变电场的主次因素,并根据能带理论,解释了畸变电场引发电击穿失效的原因。

1 麦克斯韦边值关系基本理论

根据麦克斯韦边值关系的基本理论,在电场作用下,介质界面上一般会出现面束缚电荷和电流分布,这些电荷电流的存在会使界面两侧场强发生跃变,朝向正极的空洞界面将被感应出负电荷,朝向负极的空洞界面将被感应出正电荷,分别产生新的电场,使得原有电场强度增大[13]。根据麦克斯韦边值关系公式(1)和(2),在介质2 和介质1交界处,切线方向不会产生电场突变。

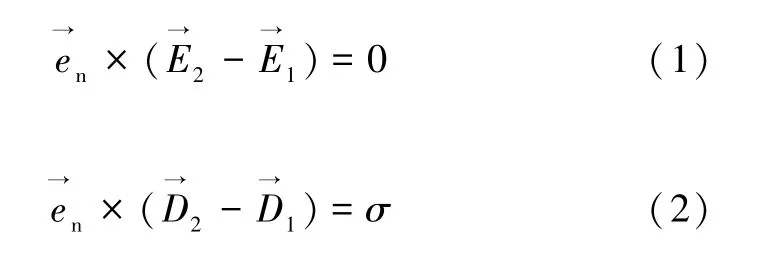
在法线方向,由于空洞内所含的气体和陶瓷介质都是不导电的材料,因此,自由电荷可近似为0,电位移矢量与电场强度的关系如公式(3)所示。由界面处自由电荷为0 以及公式(2,3),可推导出界面处电场强度的跃变关系式,见公式(4)。

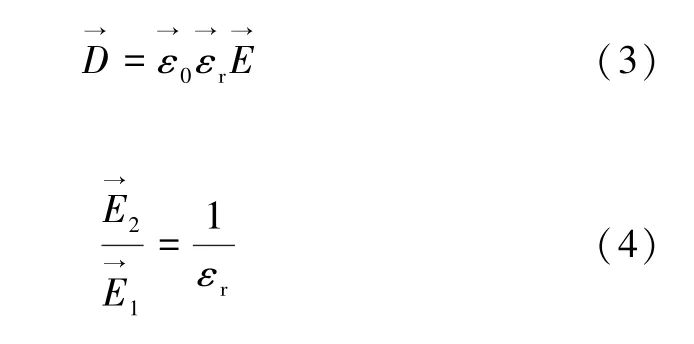
式中:ε0为空气相对介电常数;εr为介质相对介电常数。

根据上述理论,不难发现当介质中出现空洞时,就会产生空气与介质两种不同材料的界面,一方面,界面处会产生束缚电荷,会对原来的电场产生影响,而束缚电荷的多少又与空洞大小有关系;另一方面,根据公式(4),界面处两侧的场强又与各自的介电常数呈反比例关系。这两方面对电场的影响程度还需要进一步分析。

2 畸变电场变化趋势影响因素分析

2.1 不同空洞大小条件下电场强度有限元仿真

对介质空洞缺陷进行电场有限元仿真。针对某型1250 V 多层瓷介高压电容器,生产厂家提供的数据为: 介质厚度约50 μm,介质相对介电常数为460。在模拟中,为简化模型,取单个电容进行模拟,介质和电极的长度、宽度分别取4 mm,2 mm,空洞内部气体取相对介电常数为1。电容器为2 串联结构,正常工作时,每个电容承受的电压为625 V,电压施加方向从上电极向下电极,且下电极参考电位为0,基本模型见图1、图2。

图1 单个电容器模型示意图Fig.1 Schematic diagram of a single capacitor model

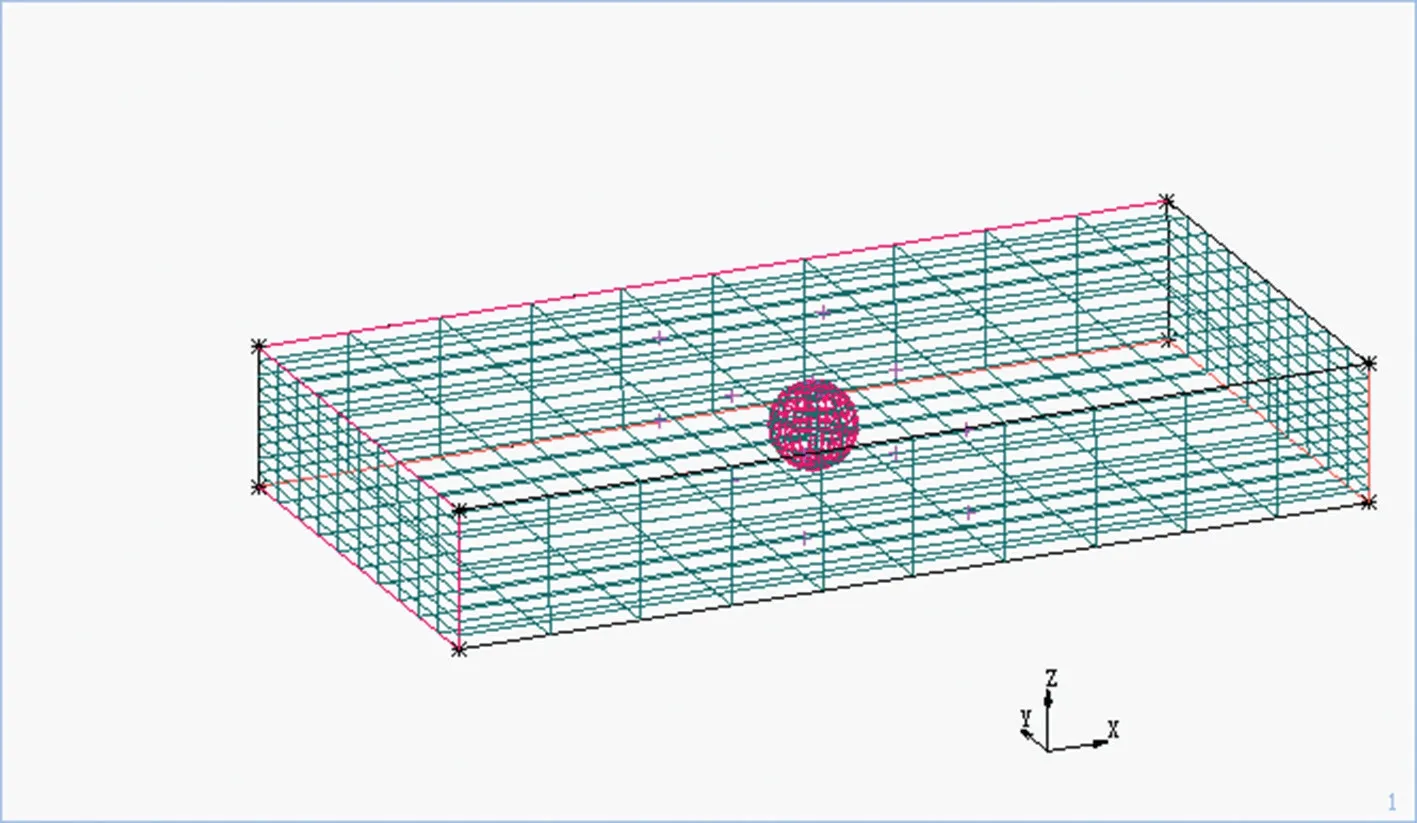
图2 空洞所在位置示意图Fig.2 Schematic diagram of pore location

对于介质空洞减小介质厚度的比例,具体取值为:0%,10%,20%,30%,40%,50%,60%。在无空洞时,如图3 所示,上下金属电极板电场强度最低,约为0,介质内部电场强度为12.5 V/μm,呈均匀分布,在均匀场强时,电场强度与所加电压的关系如公式(5)所示,分别带入电压和介质厚度,可以发现与模拟结果一致,说明模型建立基本正确。

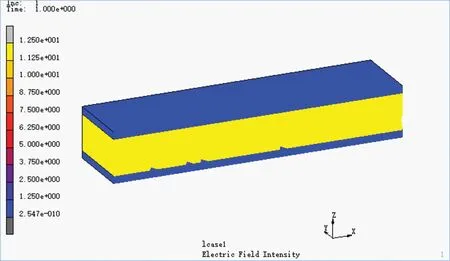
图3 1250 V 电容器无空洞电场强度模拟计算示意图Fig.3 Schematic diagram of electric field intensity simulation calculation for capacitor (1250 V) without pores

式中:E为电场强度,V/μm;U为电压,V;D为介质厚度,μm。

其余空洞大小对场强影响的有限元模拟典型代表图如图4 所示,将所有空洞大小与其对应的电场强度拟合成曲线,如图5 所示。

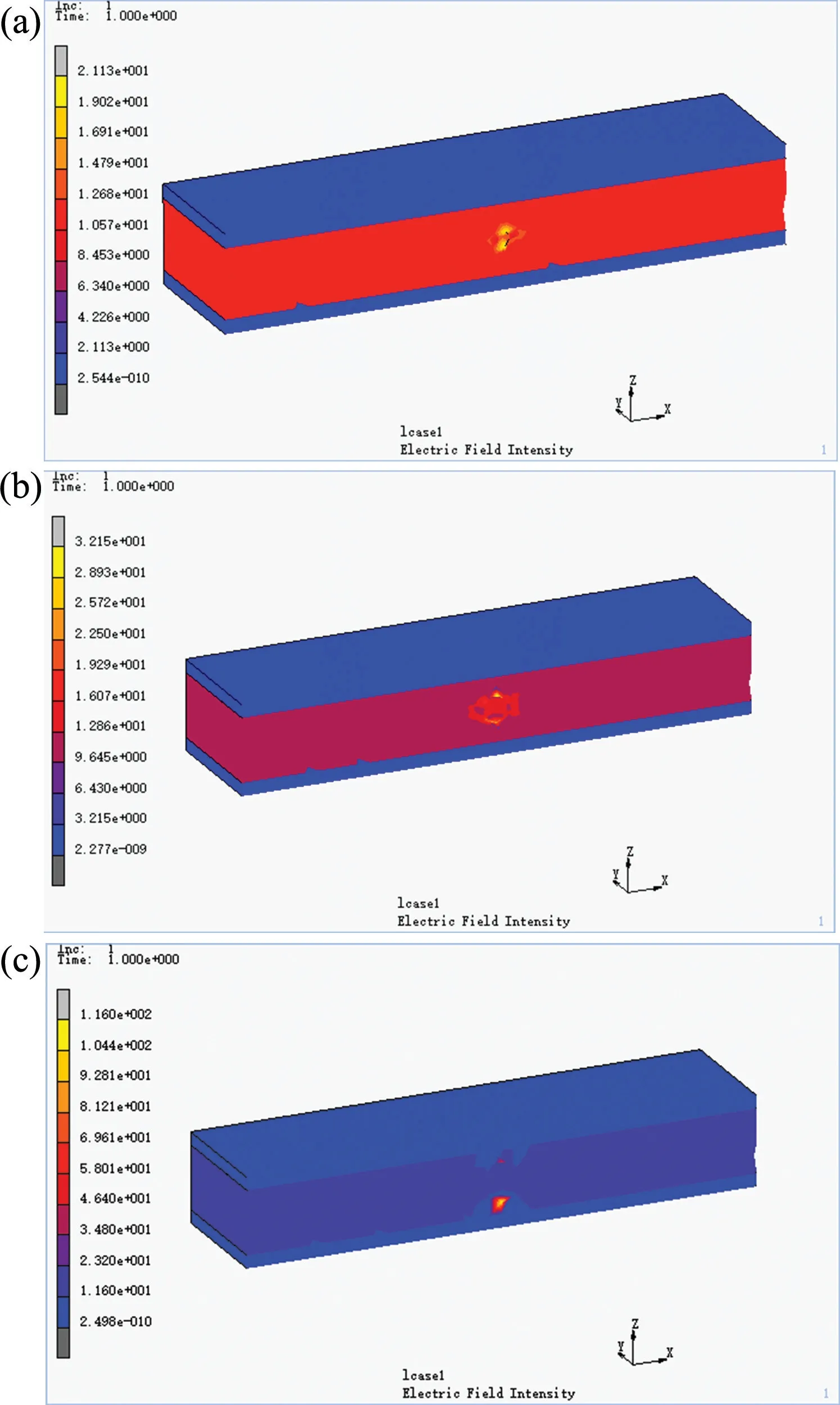
图4 (a) 20%,(b) 40%,(c) 60%空洞电容器场强模拟计算图Fig.4 Schematic diagram of electric field intensity simulation calculation for capacitor with (a) 20%,(b) 40%,(c) 60% pores

从图5 可以看出,随着空洞的增大,在其周围的场强也会增加,且趋势越来越急剧,对于1250 V,单层介质厚度为50 μm 的电容器,在空洞直径大于20 μm 时,电场强度会急剧增加。这种趋势说明,如果空洞大到一定程度,当外界出现电压波动时,空洞附近的场强增加幅度较大,就有可能达到介质本身的击穿场强而使附近区域电击穿。

图5 空洞大小与电场强度的关系Fig.5 Diagram of relationship between pore size and electric field strength

2.2 不同介电常数条件下电场强度的有限元仿真

在其他条件相同的情况下,空洞大小为减小介质厚度的60%,模拟了介质相对介电常数从1 到500 变化时空洞附近的畸变电场情况,典型的畸变电场分布情况见图6。从图6(a)可以看出,当介质相对介电常数为1 时,空洞内外一样,此时等同于空洞和介质处于同一均匀介质之中,整个区域均为均匀场强,为25 V/μm。从图6(b)～(e)可以看出,当空洞内外介电常数不一致时,空洞附近开始出现畸变电场,当相对介电常数从2 变化到500 时,最大场强值从28 V/μm 逐渐增加到35 V/μm,说明介电常数越大,空洞附近畸变电场越大。将相对介电常数与畸变电场最大值进行曲线拟合,如图7 所示,可以看出随着相对介电常数的提高,畸变电场趋于稳定。

图6 (a) εr=1,(b) εr=2,(c) εr=10,(d) εr=50,(e) εr=500 时畸变电场分布图Fig.6 Schematic diagram of distorted electric field distribution when (a) εr=1,(b) εr=2,(c) εr=10,(d) εr=50,(e) εr=500

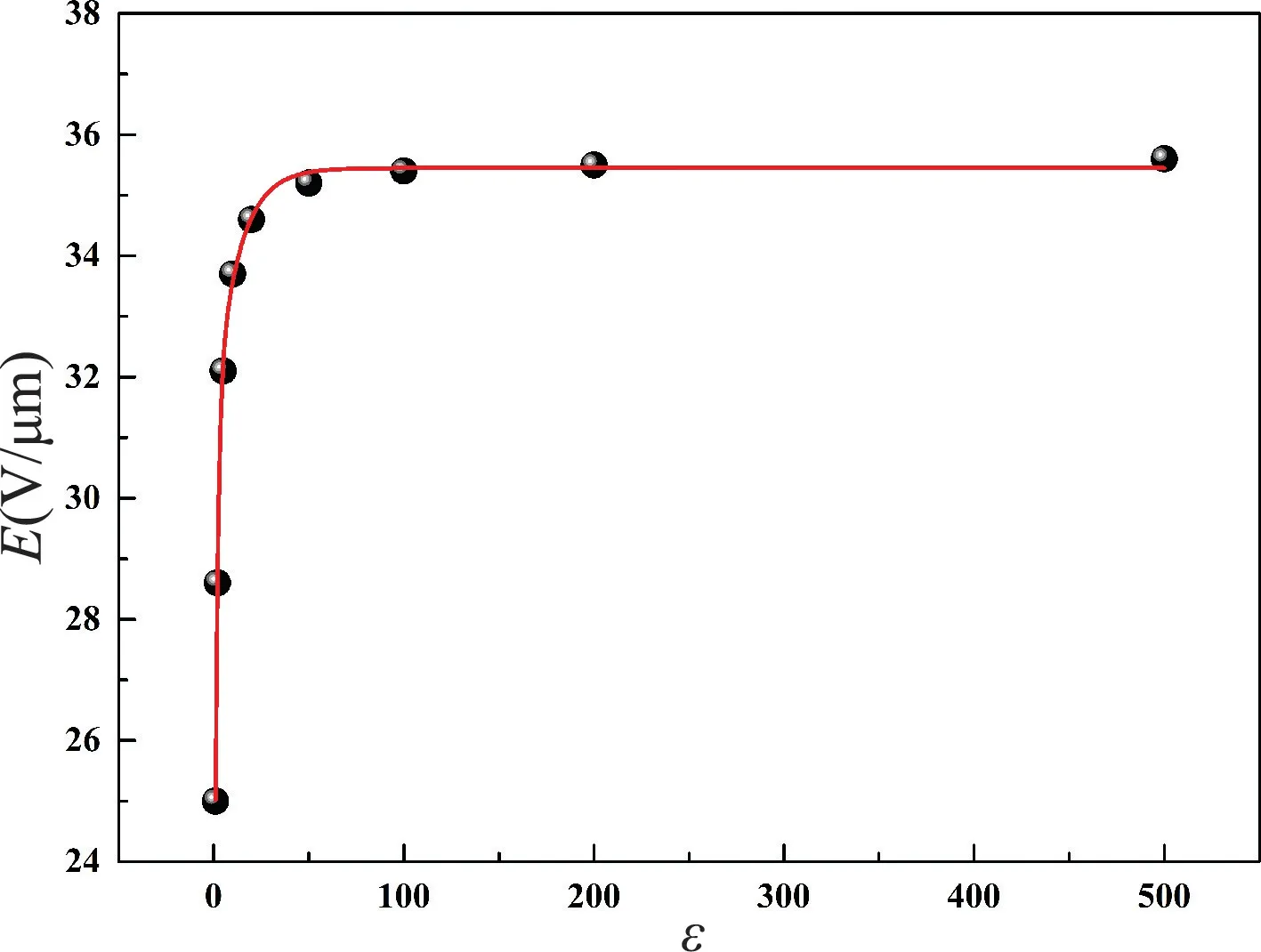
图7 相对介电常数与畸变电场关系图Fig.7 Diagram of relationship between pore size and distorted electric field strength

2.3 影响畸变电场主次因素及相关机理分析

2.3.1 空洞大小对畸变电场趋势的影响机理

从跃变关系可以看出,在界面处会产生较大的场强。但由于电荷和电场相互制约的作用,倍数关系并不是在原来的基础上增加,在空洞缺陷附近,由于场强叠加的效果,界面处两侧的场强关系也不是公式(4)的倍数关系。另从有限元仿真结果可以看出,场强随空洞尺寸增大呈幂函数增长,当空洞大到一定的程度,电场强度变化程度会越来越显著。综上所述,空洞缺陷引起的畸变电场的机理为: 在空洞界面处,根据麦克斯韦方程边值关系,界面处场强会增大;缺陷导致其周围附近产生非均匀场强,场强叠加会进一步导致某些局部区域场强继续增大;从有限元计算分析结果来看,随着空洞的增大,畸变电场呈幂函数增长趋势。因此,空洞的大小应是影响畸变电场的主要因素。

2.3.2 不同介电常数对畸变电场的影响机理

从图6(b)～(e)可以看出,当空洞内外存在介电常数差异时,在最大场强附近必然会对应出现场强较小的局部区域。根据麦克斯韦边值关系,空洞内外介质的介电常数不一样,在法线方向电场强度会发生突变,从公式(4)中可以看出,相对介电常数与电场强度呈反比例关系,所以在空洞界面附近,空洞内为场强最大处,必然会在空洞外对应产生一个场强相对较小的区域。由于空洞内空气相对介电常数为1,所以介质相对介电常数越大,在空洞内的畸变电场就越大。有限元模拟结果的趋势与麦克斯韦边值理论得到了较好的吻合。同时,从图7 也可以看出,随着相对介电常数的提高,畸变电场最大值趋于稳定,并不严格满足公式(4)的关系。

因为电荷和电场是相互制约的,电场是矢量,且在边界上还存在突变关系,因此,无法按照公式(5)计算出每点的电场强度值。相关文献[14]报道了在均匀场强中存在另一种介质时场强的分布情况,由于电势是标量,且在边界是连续的,电场强度本质上是电势的负梯度,利用拉普拉斯分离变量法首先求解出电势分布,再根据电势分布与场强的关系计算出电场强度,见公式(6)。

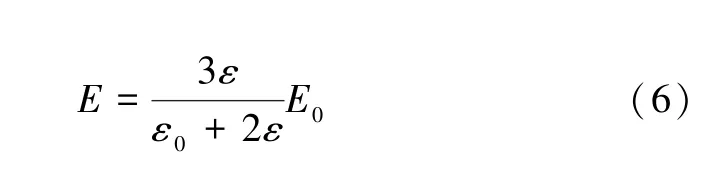
式中:E为空洞内介质的电场强度,V/μm;E0为空洞外介质的电场强度,V/μm;ε0为空洞内空气的相对介电常数;ε为空洞外介质的相对介电常数。

将空气相对介电常数1,介质相对介电常数1～500 代入公式(6),拟合成曲线,即可得到空洞附近畸变电场与介质相对介电常数的关系,如图8 所示,可以发现与图7 非常近似。从公式(6)可以看出,如果空洞外的均匀电场确定,当介质介电常数无限增大时,求极限即可得到空洞附近畸变电场最多是空洞外均匀场强的1.5 倍。

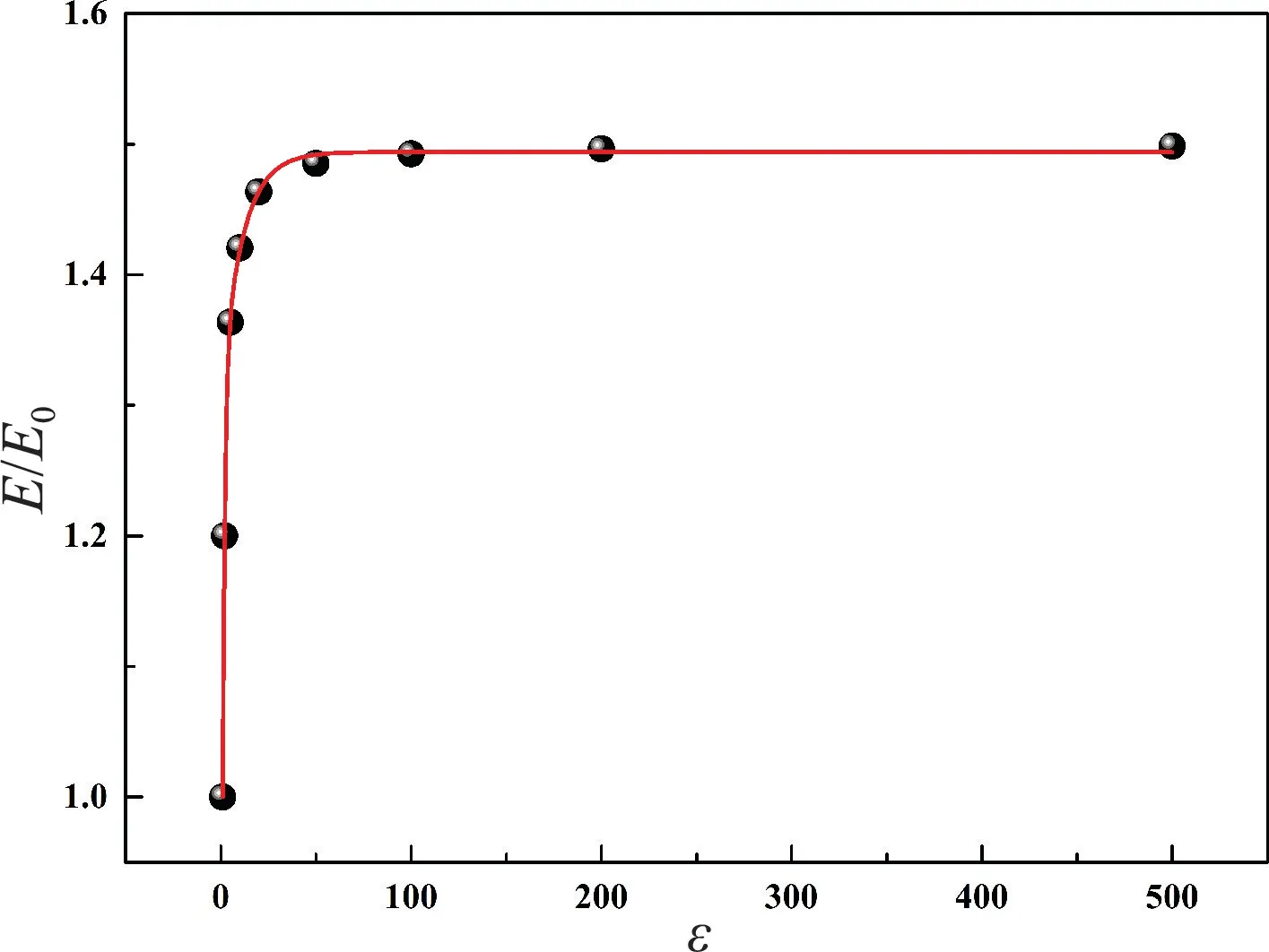
图8 根据公式(6)拟合的畸变电场与相对介电常数关系示意图Fig.8 Schematic diagram of the relationship between the distorted electric field and the relative permittivity according to formula (6)

从图6(e)可以看出,当介质相对介电常数为500时,空洞内最大场强约为35 V/μm,空洞外介质均匀场强区域场强约为25 V/μm,两者比值约为1.4,基本上与文献报道的理论吻合,说明有限元模拟计算的介质材料相对介电常数带来的影响趋势是正确的。有限元模拟计算得到的结果有微小的偏差,其原因是文献报道的理论计算是在整个空间无限大的情况,而有限元模拟计算是在介质有上下电极情况下进行的,因此,空洞上下界面必然会受上下电极分布情况的影响。从有限元分析计算结果来看,随着介电常数的增大,畸变电场增大的同时趋于稳定,最多只有均匀场强区域的1.4 倍,说明介电常数是影响畸变电场的次要因素。

3 畸变电场产生的危害性分析

根据能带理论,畸变电场引发电击穿失效的机理可解释为[15]: 固体中电子处于不同的能级上,对绝缘体而言只存在空带和满带,带隙高达10 eV,所以绝缘体在通常情况下不导电,具有较好的绝缘性质。空洞是一种常见的体缺陷,体缺陷的产生会引入缺陷能级,降低禁带宽度,减小电导激活能。因此,在材料上加载电场时,电子更容易从电场中获取足够的能量,由价带跃迁至导带,形成部分占据能带。这时介质具有一定导电性,且处于部分占据能带中的电子或空穴可以在电场的加速下迅速获得能量。当场强较大时,电子获取较大能量,从而与原子碰撞,使价键断裂而产生电子空穴对,产生的电子空穴对由相同原理又激发二代电子空穴对,如此循环导致产生较大的电流,大量的电子冲击电容器内部较为薄弱处的晶格,原子间的价键加速断裂,形成泄放通道,最终导致器件击穿,击穿机理示意图见图9。

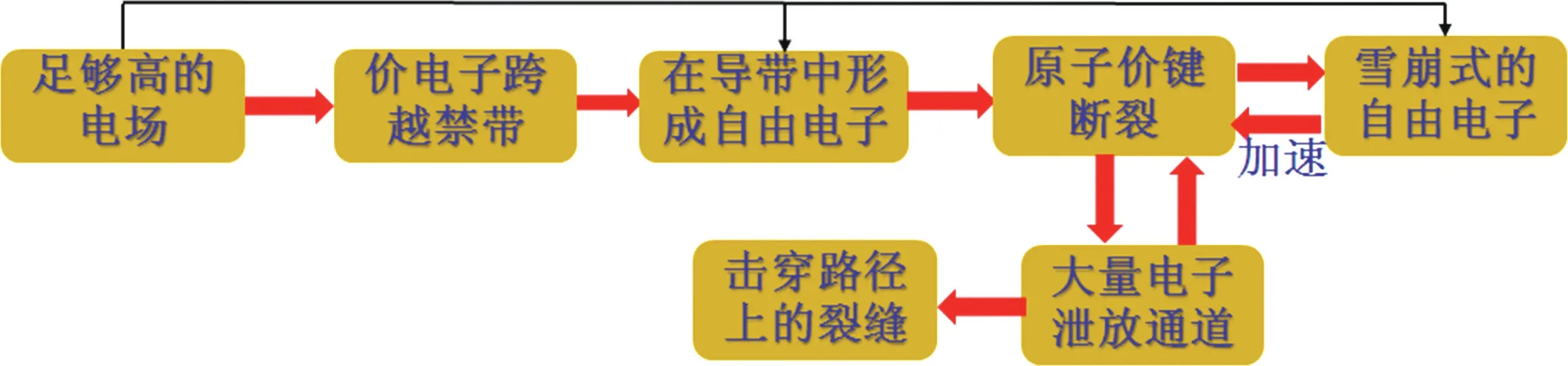
图9 电击穿机理示意图Fig.9 Schematic diagram of mechanisms for electrical breakdown

4 结论

本文在现有元器件失效分析类文献的基础上,以陶瓷电容内部空洞缺陷大小为对象,利用有限元分析的基本思路,结合麦克斯韦边值关系理论,分析了空洞缺陷大小、介质介电常数对畸变电场的影响趋势,并阐述了相关机制。结果表明,空洞大小是影响畸变电场的主要因素。随着空洞增大,畸变电场呈幂函数增长,对1250 V 电容器来说,当空洞直径所占介质厚度的比例超过40%后,电场强度将会急剧增大,这种趋势说明了局部场强集中现象将加剧严重。对用户使用来说,当外界出电压波动时,就有可能达到介质本身的击穿场强而使附近区域电击穿,从而对可靠性造成较大影响。根据麦克斯韦边值关系理论,出现上述趋势的本质因素是不同介质界面处法线方向会发生场强跃变,同时,还由于空洞界面与上下电极在库仑力的作用下产生束缚电荷,以及界面几何形状产生场强叠加效果。相关分析结果对于采用有限元方法分析元器件内部微小缺陷对性能的影响,以及结合用户使用场景制定相应的评价依据具有一定的参考意义。