输入磁滞的非线性系统事件触发有限时间控制
马灿洪,黄峥,严彦成,巩琪娟,黄堃锋
(广州大学 机械与电气工程学院,广州 510006)
0 引言
在实际工业控制系统中,输入磁滞现象普遍存在,这使系统的跟踪性能受到限制,严重影响控制系统的收敛时间和稳定性[1]。因此如何补偿这种输入磁滞现象,使系统具有更好的性能是该领域的研究热点。近年来,许多学者针对这一问题提出了解决方案:文献[2-3]针对具有PI 磁滞模型的非线性系统,通过构造磁滞逆模型来补偿输入磁滞的影响。文献[4]基于磁滞逆模型,设计了一种利用自适应磁滞逆函数来消除未知输入磁滞的自适应控制方法。由于构造磁滞逆矩阵非常复杂,文献[5]提出了一种自适应神经控制方法,以保证系统具有一定的跟踪精度。然而,上述方法都需要消耗大量的沟通资源,而在实际控制系统中通信资源非常有限,因此如何使控制系统在较少控制量下保持良好性能是一个值得深入研究的问题。
为了保持有效的网络控制,在实践中应尽量减少有限的通信资源的使用。例如,文献[6]设计了一种基于固定阈值策略的事件触发控制方案,该方案具有简单方便的突出优点,但同时产生了大量的冗余数据传输。为解决该问题,文献[7]设计了一个相对阈值事件触发方案;文献[8]提出了基于固定和相对组合阈值策略的触发方案。
另一方面,目前大多数控制系统都是无限时间收敛控制,存在收敛时间过长等问题。为此,文献[8]针对具有参数不确定性的非线性系统,提出了一种自适应有限时间控制方法,为连续自治系统设计了有限时间控制系统。而该系统中的非线性函数要求都满足线性增长条件,但由于建模方法的限制或外界干扰,非线性函数往往是完全未知的。在这种情况下,可能不满足线性增长条件。为了消除这一限制,文献[10]提出了一种新的非线性系统有限时间稳定性判据,消除了线性增长条件。
综上所述,考虑输入磁滞后,不确定非线性系统的补偿控制设计在用于非线性控制增益时难度较大。在有限通信资源下,设计具有输入磁滞的不确定非线性系统的事件触发有限时间控制具有十分重要的意义。因此,本文提出了一种模糊自适应事件触发有限时间约束控制方法,其主要有以下2个创新点。
(1)文献[2-5]所提出的方法以牺牲系统的暂态性能和收敛时间为代价,解决了输入磁滞问题。而本设计提出了一种模糊自适应事件触发控制方法,既能实现输入磁滞的动态补偿,又能保证系统在有限时间内收敛。
(2)为了节省通信资源,提出了一种事件触发控制策略。在此基础上,又提出了一种保证系统在有限时间内跟踪性能的有限时间控制方法。利用所提出的控制方法,系统中的非线性函数可以是完全未知的,并且只要求它们是连续的。
1 模型与问题陈述
1.1 系统模型的分析
本文考虑一类具有未知磁滞的不确定非线性系统如下
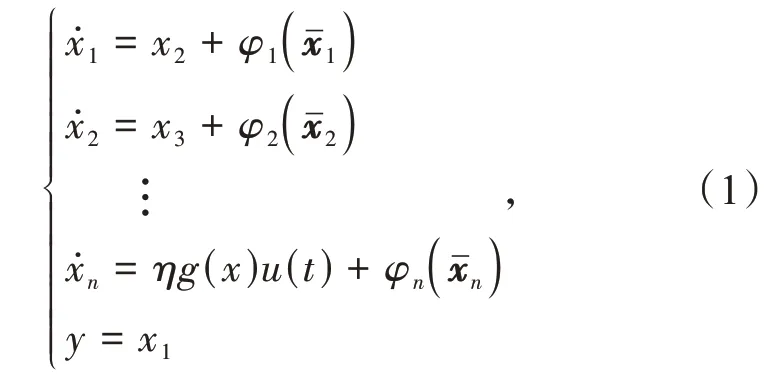
式 中:x=[x1,…,xn]T∈Rn是 系 统 的 状 态 变 量;φi(·) ∈R,(i= 1,…,n)是系统中的不确定非线性函数;g(x) ∈R是系统中已知的光滑非线性函数;u(t)是系统的输入信号;η∈R表示未知的常量参数。
考虑执行器的磁滞将设计的控制信号转换为vc=M(uc),表示输出信号。根据文献[11-13],磁滞模型可以表示为

1.2 事件触发控制器的设计
由于通信信道带宽和计算能力的限制,为了节省通信网络的网络资源,考虑以下事件触发方案

式中:c>0,v>0,k>0,ℓ >0且(k- 1)(ℓ - 1) = 1。
1.3 近似函数的研究
在模糊自适应控制方案中,采用模糊逻辑系统(FLS)逼近未知的连续函数。

假设1:g(x) ≠0;η≠0,η的符号已知。
假设2:期望信号r已知且有界,存在n+ 1 阶导数。
2 自适应事件触发补偿控制的设计与分析
本节针对通信资源有限的磁滞系统,设计了一种扩展的自适应模糊事件触发控制方案,以保证跟踪性能。
该系统中所有信号都是有界的,事件触发机制保证了跟踪误差性能。
2.1 模糊自适应补偿反步设计
首先,引入以下误差方程


下一节将详细说明步骤n和本文所提出的事件触发机制。
2.2 模糊自适应补偿事件触发控制器设计
本文提出了一种事件触发通信方案,其触发条件基于控制信号uc(t)的变化,是一种非周期性的事件触发机制。具体来说,当控制信号uc(t)的变化超过一个阈值时,才对触发器的输出信号进行更新,使更新间隔变长,从而节省资源。在系统运行过程中,随着系统状态逐渐趋于稳定,触发器更新的频率逐渐减小,只需消耗更小的资源便能保持系统稳定。
事件触发方案的定义如下


那么经过引理1分析,式(34)可表示为

式 中:γ̂n(0),β(0),ω(0) ≥0;qn,C1,C2是 正 设 计 参数。结合虚拟控制律式(25)和自适应律式(37)、式(38)、式(39),根据引理1和引理3分析可得

2.3 系统的稳定性分析
定理1:考虑具有函数增益输入的不确定非线性系统式(1),不确定输入磁滞模型式(2),中间虚拟控制器式(12)、式(18)、式(25),基于事件触发策略的控制器式(28),参数自适应律式(16)、式(22)、式(37)、式(38)和式(39)。以下特性得到保证:(1)系统中所有信号都是有界的;(2)所有的输出信号都能在有限时间内定位到给定信号的一小块区域;(3)有效地避免Zeno行为。
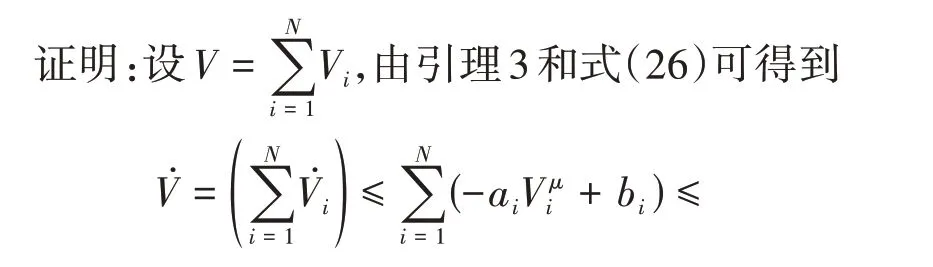

由式(43)可以推导出Vi是有界的。zi,γ͂i,β͂和ῶ都是有界的,另外γi,β和ω都是常量,因此γ̂i,β̂和ω̂也是有界的。同时,z1=y-r和r是有界的,表明y是有界的。可以看出,x1在概率上是半全局一致有界的。α1由z1和γ̂1组成,因此α1有界,意味着x1也是有界的。同理,xi,i= 3,…,n都是有界的。这意味着控制律us也有界。因此,闭环系统的所有输出和跟踪误差都是有界的。
注2:0 <kj,0<1;zi,γ͂i,β͂,αi,ῶ都很小且有界。因此,所有的输出都能定位到给定信号的一个小区域。
根据上述分析,可以证明本文提出方法可以在有限时间内,使得所有的输出yj,j= 1,2,…,n都能定位到给定信号rj,j= 1,2,…,n的一个小区域。



3 仿真试验及结果


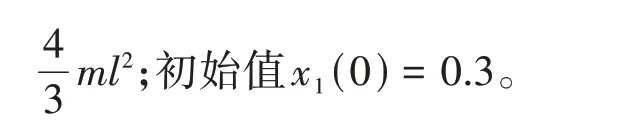
仿真结果表明:该方法保证了单连杆机械臂的跟踪控制,且实现系统的全局一致有界状态,保证系统在有限时间内的性能。系统输出y(t)和参考输出r(t)如图1 所示。跟踪误差如图2 所示。从图1、图2 可知,在输出初值为0.3 的状态下,系统可以在有限时间内实现快速跟踪,使跟踪误差从0.03迅速接近0,并保持在0.05的预期误差范围内波动,后续系统输出与参考输入几乎重合,实现精准跟踪。
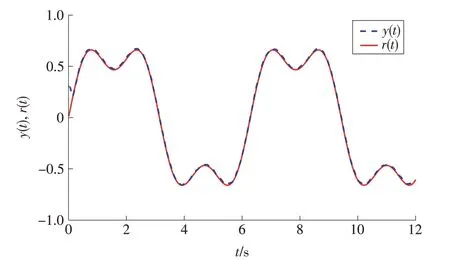
图1 系统输出y(t)和参考输出r(t)Fig.1 System output y(t) and reference output r(t)

图2 跟踪误差Fig.2 Tracking error
事件触发的控制输入如图3所示。执行间隔如图4 所示。由图3 可知,蓝线为连续控制信号输入,红线为阶梯式事件触发控制输入,可以很好地节省带宽资源。由图4 可知,带宽的节省范围为0.02~0.44 s。

图3 事件触发的控制输入Fig.3 Event-triggered control input

图4 执行间隔Fig.4 Inter-execution interval
各时间段触发次数见表1。由表1 可知,在[0~2) s 节省了86.0%的带宽,在[2~4) s 节省了89.0%的带宽,在[4~6) s 节省了88.5%的带宽,在[6~10]s 节省了90.5%的带宽,在10 s 内节省88.9%的带宽。由此可知,该方法既保证了单臂的跟踪控制,又达到了节省系统带宽的效果。

表1 各时间段触发次数Table 1 Trigger times in each time period
4 结论
针对具有输入滞后的不确定非线性系统,提出了一种模糊自适应事件触发有限时间约束控制方法。为了消除输入滞后的影响,同时解决通信资源有限的问题,提出了一种模糊自适应事件触发控制策略。在此基础上,提出了一种事件触发的有限时间控制方法,实现了闭环系统的有限时间收敛,同时节约了通信带宽。仿真结果表明了该方法具有一定有效性,还避免了Zeno行为。

